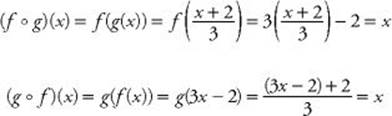SAT SUBJECT TEST MATH LEVEL 1
FUNCTIONS
CHAPTER 15
Functions and Graphs
COMPOSITION OF FUNCTIONS
A more important way to combine two functions is to form their composition: f o g.
The definition of composition is given in KEY FACT N6.
Key Fact N6
The composition of two functions f and g is (f o g)(x) = f (g(x)).
The composition of f and g can be formed only if some of the numbers in the range of g are in the domain of f.
EXAMPLE 12: If f(x) = 
and g (x) = –x2 – 2, then (f o g)(x) does not exist. For every real number x, g (x) is negative, but no negative number is in the domain of f.
EXAMPLE 13: Let f (x) = 2x + 3 and g (x) = x2 – 1.
To find (f o g)(3) you have two choices:
(1) You can determine f (g (x)) and then plug in x = 3:
(f o g)(x) = f (g(x)) = 2(g (x)) + 3 = 2(x2 – 1) + 3 = 2x2 – 2 + 3 = 2x2 + 1
Then (f o g)(3) = 2(3)2 + 1 = 2(9) + 1 = 19
or
(2) You can calculate (f o g)(3) directly:
(f o g)(3) = f (g (3)) = f (8) = 2(8) + 3 = 19
EXAMPLE 14: Let f and g be the same functions as in Example 13: f (x) = 2x + 3 and g (x) = x2 – 1. Then:
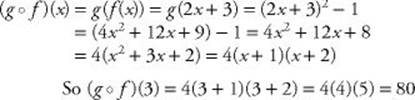
Of course, (g o f )(3) could have been calculated directly:
(g o f )(3) = g (f (3)) = g (9) = 92 – 1 = 80
Notice that, in general, (f o g) 
(g o f ). In Examples 13 and 14, you saw:
(f o g)(3) = 19 and (g o f )(3) = 80
It is possible, however, to have functions f and g for which (f o g) = (g o f ).
EXAMPLE 15: Let f (x) = 3x – 2 and 
Then:
