SAT SUBJECT TEST MATH LEVEL 2
PART 2
![]()
REVIEW OF MAJOR TOPICS
![]()
CHAPTER 1
Functions

1.2 Polynomial Functions
![]()
HIGHER-DEGREE POLYNOMIAL FUNCTIONS
Polynomial functions of degree greater than two (largest exponent greater than 2) are usually treated together since there are no simple formulas, such as the general quadratic formula, that aid in finding zeros.
Here are five facts about the graphs of polynomial functions:
1. They are always continuous curves. (The graph can be drawn without removing the pencil from the paper.)
2. If the largest exponent is an even number, both ends of the graph leave the coordinate system either at the top or at the bottom:
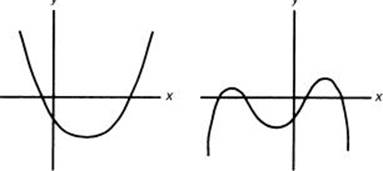
3. If the largest exponent is an odd number, the ends of the graph leave the coordinate system at opposite ends.
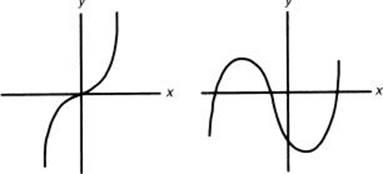
Facts (2) and (3) describe the end behavior of a polynomial.
4. If all the exponents are even numbers, the polynomial is an even function and therefore symmetric about the y-axis.
y = 3x4 + 2x2 – 8
5. If all the exponents are odd numbers and there is no constant term, the polynomial is an odd function and therefore symmetric about the origin of the coordinate system.
y = 4x5 + 2x3 – 3x
A polynomial of degree n has n zeros. The zeros of polynomials with real coefficients can be real or imaginary numbers, but imaginary zeros must occur in pairs. For example, if the degree of a polynomial is 6, there are 6 real zeros and no imaginary zeros; 4 real zeros and 2 imaginary ones; 2 real zeros and 4 imaginary ones, or 6 imaginary zeros. Moreover, real zeros can occur more than once.
If a real zero occurs n times, it is said to have multiplicity n. If a zero of a polynomial has even multiplicity, its graph touches, but does not cross, the x-axis. For example, in the polynomial f(x) = (x – 3)4, 3 is a zero of multiplicity 4, and the graph of f(x) is tangent to the x-axis at x = 3. If a zero of a polynomial has odd multiplicity, its graph crosses the x-axis. For example, in the polynomial f(x) = (x – 1)5, 1 is a zero of multiplicity 5, and the graph of f(x) crosses the x-axis at x = 1.
The multiplicity of a real zero is counted toward the total number of zeros. For example, the polynomial f(x) = (x – 5)(x + 3)4(x2 + 6) has degree 7: one zero (5) of multiplicity 1; one zero (–3) of multiplicity 4; and two imaginary zeros (i ![]() and –i
and –i ![]() ).
).
There are 5 facts that are useful when analyzing polynomial functions.
1. Remainder theorem—If a polynomial P(x) is divided by x – r (where r is any constant), then the remainder is P(r).
Divide P(x) = 3x5 – 4x4 – 15x2 – 88x – 12 by x – 3.
Enter P(x) into Y1, return to the home screen, and evaluate Y1(3) = –6. The remainder is –6 when you divide P(x) by x – 3.
2. Factor theorem —r is a zero of the polynomial P(x) if and only if x – r is a divisor of P(x).
Is x – 99 a factor of x4 – 100x3 + 97x2 + 200x – 198?
Call this polynomial P(x) and evaluate P(99) using your graphing calculator. Since P(99) = 0, the answer to the question is “Yes.”
3. Rational zero (root) theorem—If ![]() is a rational zero (reduced to lowest terms) of a polynomial P(x) with integral coefficients, then p is a factor of a0 (the constant term) and q is a factor of an (the leading coefficient).
is a rational zero (reduced to lowest terms) of a polynomial P(x) with integral coefficients, then p is a factor of a0 (the constant term) and q is a factor of an (the leading coefficient).
What are the possible rational zeros of P(x) = 3x3 + 2x2 + 4x – 6?
The divisors of the constant term –6 are ±1, ±2, ±3, ±6, and the divisors of the leading coefficient 3 are ±1, ±3. The 12 rational numbers that could possibly be zeros of P(x) are ±1, ±2, ![]() , the ratios of all numbers in the first group to all numbers in the second.
, the ratios of all numbers in the first group to all numbers in the second.
4. If P(x) is a polynomial with real coefficients, then complex zeros occur as conjugate pairs. (For example, if p + qi is a zero, then p – qi is also a zero.)
If 3 + 2i, 2, and 2 – 3i are all zeros of P(x) = 3x5 – 36x4 + 2x3 – 8x2 + 9x – 338, what are the other zeros?
Since P(x) must have five zeros because it is a fifth-degree polynomial, and since the coefficients are real and the complex zeros come in conjugate pairs, the two remaining zeros must be 3 – 2i and 2 + 3i.
5. Descartes” rule of signs—The number of positive real zeros of a polynomial P(x) either is equal to the number of changes in the sign between terms or is less than that number by an even integer. The number of negative real zeros of P(x) either is equal to the number of changes of the sign between the terms of P(–x) or is less than that number by an even integer. 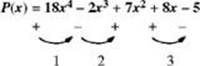
Three sign changes indicate there will be either one or three positive zeros of P(x).
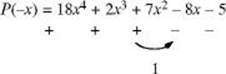
One sign change indicates there will be exactly one negative zero of P(x).
EXERCISES
1. P(x) = ax4 + x3 – bx2 – 4x + c. If P(x) increases without bound as x increases without bound, then, as x decreases without bound, P(x)
(A) increases without bound
(B) decreases without bound
(C) approaches zero from above the x-axis
(D) approaches zero from below the x-axis
(E) cannot be determined
2. Which of the following is an odd function?
I. f(x) = 3x3 + 5
II. g(x) = 4x6 + 2x4 – 3x2
III. h(x) = 7x5 – 8x3 + 12x
(A) only I
(B) only II
(C) only III
(D) only I and II
(E) only I and III
3. How many possible rational roots are there for 2x4 + 4x3 – 6x2 + 15x – 12 = 0?
(A) 4
(B) 6
(C) 8
(D) 12
(E) 16
4. If both x – 1 and x – 2 are factors of x3 – 3x2 + 2x – 4b, then b must be
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
5. If 3x3 – 9x2 + Kx – 12 is divisible by x – 3, then K =
(A) –40
(B) –3
(C) 3
(D) 4
(E) 22
6. Write the equation of lowest degree with real coefficients if two of its roots are –1 and 1 + i.
(A) x3 + x2 + 2 = 0
(B) x3 – x2 – 2 = 0
(C) x3 – x + 2 = 0
(D) x3 – x2 + 2 = 0
(E) none of the above