SAT SUBJECT TEST MATH LEVEL 2
PART 2
REVIEW OF MAJOR TOPICS
CHAPTER 1
Functions
1.3 Trigonometric Functions and Their Inverses
ARCS AND ANGLES
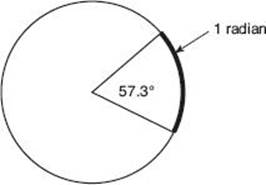
Although the degree is the chief unit used to measure an angle in elementary mathematics courses, the radian has several advantages in more advanced mathematics. A radian is one radius length. The circle shown in the figure below has radius r. The circumference of this circle is 360°, or 2π radians, so one radian is 
.
EXAMPLES
1. In each of the following, convert the degrees to radians or the radians to degrees. (If no unit of measurement is indicated, radians are assumed.)
(A) 30°
(B) 270°
(C) 
(D) 
(E) 24
|
TIP Although R is used to indicate radians, a radian actually has no units, so the use of R is optional. |
SOLUTIONS
(A) To change degrees to radians multiply by 
, so 30° = 30° 
.
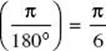(B) 270°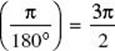 
(C) To change radians to degrees, multiply by 
, so 
(D) 
(E)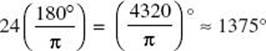 
In a circle of radius r inches with an arc subtended by a central angle of 
measured in radians, two important formulas can be derived. The length of the arc, s, is equal to r, and the area of the sector, AOB, is equal to 
.
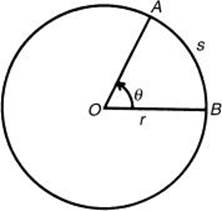
2. Find the area of the sector and the length of the arc subtended by a central angle of 
radians in a circle whose radius is 6 inches.
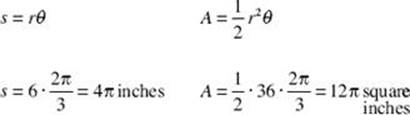
3. In a circle of radius 8 inches, find the area of the sector whose arc length is 6π inches.
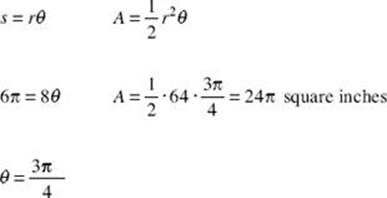
4. Find the length of the radius of a circle in which a central angle of 60° subtends an arc of length 8π inches.
The 60° angle must be converted to radians:
60° = 60° 
radians = 
radians
Therefore,
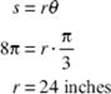
EXERCISES
1. An angle of 30 radians is equal to how many degrees?
(A) 
(B) 
(C) 
(D) 
(E) 
2. If a sector of a circle has an arc length of 2π inches and an area of 6π square inches, what is the length of the radius of the circle?
(A) 1
(B) 2
(C) 3
(D) 6
(E) 12
3. If a circle has a circumference of 16 inches, the area of a sector with a central angle of 4.7 radians is
(A) 10
(B) 12
(C) 15
(D) 25
(E) 48
4. A central angle of 40° in a circle of radius 1 inch intercepts an arc whose length is s. Find s.
(A) 0.7
(B) 1.4
(C) 2.0
(D) 3.0
(E) 40
5. The pendulum on a clock swings through an angle of 25°, and the tip sweeps out an arc of 12 inches. How long is the pendulum?
(A) 1.67 inches
(B) 13.8 inches
(C) 27.5 inches
(D) 43.2 inches
(E) 86.4 inches