SAT SUBJECT TEST MATH LEVEL 2

PART 2

REVIEW OF MAJOR TOPICS

CHAPTER 1
Functions

1.5 Rational Functions and Limits

The function f is a rational function if and only if f(x) = , where p(x) and q(x) are both polynomial functions and q(x) is not zero. As a general rule, the graphs of rational functions are not continuous (i.e., they have holes, or sections of the graphs are separated from other sections by asymptotes). A point of discontinuity occurs at any value of x that would cause q(x) to become zero.

If p(x) and q(x) can be factored so that f(x) can be reduced, removing the factors that caused the discontinuities, the graph will contain only holes. If the factors that caused the discontinuities cannot be removed, asymptotes will occur.

EXAMPLES

1. Sketch the graph of f(x) = .

There is a discontinuity at x = –1 since this value would cause division by zero. The fraction = (x – 1), and so the graph of f(x) is the same as the graph of y = x – 1 except for a hole at x = – 1.

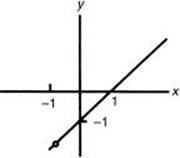
You could also enter this function on the graphing calculator and get the graph shown above, but it is unlikely that you would see the hole at (–1,0).

2. Sketch the graph of f(x) = .

Since this fraction cannot be reduced, and x = 2 would cause division by zero, a vertical asymptote occurs when x = 2. This is true because, as x approaches very close to 2, f(x) gets either extremely large or extremely small. As x becomes extremely large or extremely small, f(x) gets closer and closer to zero. This means that a horizontal asymptote occurs when y = 0. Plotting a few points indicates that the graph looks like the figure below.

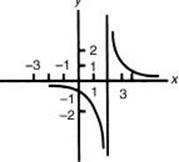
Vertical and horizontal asymptotes can also be described using limit notation. In this example you could write

   to mean f(x) gets closer to 0 as x gets arbitrarily large or small

   to mean f(x) gets arbitrarily large as x approaches 2 from the right

   to mean f(x) gets arbitrarily small as x approaches 2 from the left

If you entered this function into a TI-83 calculator, your graph will show what appears to be an asymptote. (Actually, the graphing calculator connects the pixel of the largest x-coordinate for which the y-coordinate is negative to the pixel of the smallest x-coordinate for which the y-pixel is positive.) The TI-84 calculators do not connect these two pixels. In either case, you can “read” the graph to determine the two infinite limits.

3. What does equal?

Since reduces to x – 1,

Although the window settings on your calculator may not make it possible to see the hole at x = 1, you can determine the limit of this function as x approaches 1 from both sides by using the table feature. Select Ask for Indpnt; go to TABLE; enter values of x that get progressively closer to 1 from below (e.g., 0.9, 0.99, 0.999, etc.) and above (e.g., 1.1, 1.01, 1.001, etc.); and watch y get closer to 1.

4. What does equal?

Since “problems” occur only when division by zero appears imminent, this example is extremely easy. As x gets closer and closer to 2, 3x + 5 seems to be approaching closer and closer to 11. Therefore, .

5. What does equal?

The numerator is always positive, so the graph of this rational function has a vertical asymptote. As x approaches 2 from the right (i.e., 2.1, 2.01, 2.001, . . .), the denominator approaches zero from the right so gets larger and larger and approaches positive infinity. As x approaches 2 from the left (i.e., 1.9, 1.99, 1.999, . . .), the denominator approaches zero from the left so gets smaller and smaller and approaches negative infinity. Thus, does not exist since and .

As in the previous example, you could enter this function into your graphing calculator. Then, with an appropriate window, you could determine the infinite limits as x approaches 2 from the left and right.

6. If

As x approaches zero, 3x + 2 approaches 2, in spite of the fact that f(x) = 0 when x = 0. Therefore, .

7. What does equal?

As x gets larger and larger, the x² terms in the numerator and denominator “dominate” in the sense that the terms of lower degree become negligible. Therefore, the larger x gets, the more the rational function looks like .

You can also see this by dividing each term of the numerator and denominator by x², the highest power of x.

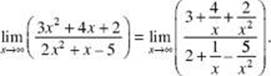
Now, as , each approaches zero. Thus, the entire fraction approaches . Therefore, .

To use a graphing calculator to find this limit, enter the function, and use the TABLE in Ask mode to enter larger and larger x values. The table will show y values closer and closer to 1.5.

EXERCISES

1. To be continuous at x = 1, the value of must be defined to be equal to

  (A) –1

  (B) 0

  (C) 1

  (D)

  (E) 4

2. If 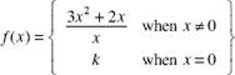, what must the value of k be equal to in order for f(x) to be a continuous function?

  (A)

  (B)

  (C) 0

  (D) 2

  (E) No value of k can make f(x) a continuous function.

3. 

  (A) 0

  (B)

  (C)

  (D)

  (E) This expression is undefined.

4. 

  (A)

  (B) 0

  (C)

  (D)

  (E)

5. Which of the following is the equation of an asymptote of ?

  (A)

  (B) x = 1

  (C)

  (D)

  (E) y = 1

Answers and Explanations

Rational Functions and Limits

All of these exercises can be completed with the aid of a graphing calculator as described in the example.

1. (D) Factor and reduce: 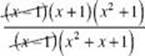. Substitute 1 for x and the fraction equals .

2. (D) Factor and reduce the fraction, which becomes 3x + 2. As x approaches zero, this approaches 2.

3. (B) Factor and reduce 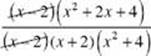. Substitute 2 for x and the fraction equals .

4. (D) Divide numerator and denominator through by x². As x , the fraction approaches .

5. (D) Factor and reduce . Therefore a vertical asymptote occurs when 3x – 1 = 0 or , but this is not an answer choice. As x , . Therefore, is the correct answer choice.