SAT SUBJECT TEST MATH LEVEL 2
PART 2
![]()
REVIEW OF MAJOR TOPICS
![]()
CHAPTER 1
Functions

1.6 Miscellaneous Functions
![]()
PARAMETRIC EQUATIONS
At times, it is convenient to express a relationship between x and y in terms of a third variable, usually denoted by a parameter t. For example, parametric equations x = x(t), y = y(t) can be used to locate a particle on the plane at various times t.
EXAMPLES
1. Graph the parametric equations 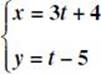
Select MODE on your graphing calculator, and select PAR. Enter 3t + 4 into X1T and t – 5 into Y1T. The standard window uses 0 for Tmin and 6.28… (2π) for Tmax along with the usual ranges for x and y. The choice of 0 for Tmin reflects the interpretation of t as “time.” With the standard window, the graph looks like the figure below.
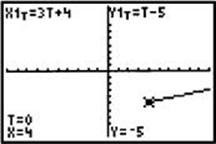
If you use TRACE, the cursor will begin at t = 0, where (x,y) = (4,–5). As t increases from 0, the graph traces out a line that ascends as it moves right.
It may be possible to eliminate the parameter and to rewrite the equation in familiar xy-form. Just remember that the resulting equation may consist of points not on the graph of the original set of equations.
2. Eliminate the parameter and sketch the graph 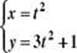
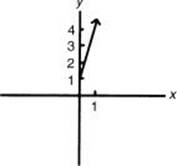
Substituting x for t2 in the second equation results in y = 3x + 1, which is the equation of a line with a slope of 3 and a y-intercept of 1. However, the original parametric equations indicate that x ![]() 0 and y
0 and y ![]() 1 since t2 cannot be negative. Thus, the proper way to indicate this set of points without the parameter is as follows: y = 3x + 1 and x
1 since t2 cannot be negative. Thus, the proper way to indicate this set of points without the parameter is as follows: y = 3x + 1 and x ![]() 0. The graph is the ray indicated in the figure.
0. The graph is the ray indicated in the figure.
3. Sketch the graph of the parametric equations ![]()
Replace the parameter ![]() with t, and enter the pair of equations. The graph has the shape of an ellipse, elongated horizontally, as shown in this diagram.
with t, and enter the pair of equations. The graph has the shape of an ellipse, elongated horizontally, as shown in this diagram.
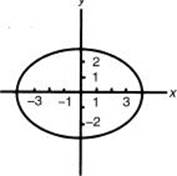
It is possible to eliminate the parameter, ![]() , by dividing the first equation by 4 and the second equation by 3, squaring each, and then adding the equations together.
, by dividing the first equation by 4 and the second equation by 3, squaring each, and then adding the equations together.
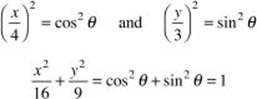
Here, ![]() =1 is the equation of an ellipse with its center at the origin, a = 4, and b = 3 (see Coordinate Geometry). Since –1
=1 is the equation of an ellipse with its center at the origin, a = 4, and b = 3 (see Coordinate Geometry). Since –1 ![]() cos
cos ![]()
![]() 1 and –1
1 and –1 ![]() sin
sin ![]()
![]() 1, –4
1, –4 ![]() x
x ![]() 4 and –3
4 and –3 ![]() y
y ![]() 3 from the two parametric equations. In this case the parametric equations do not limit the graph obtained by removing the parameter.
3 from the two parametric equations. In this case the parametric equations do not limit the graph obtained by removing the parameter.
EXERCISES
1. In the graph of the parametric equations ![]()
(A) x ![]() 0
0
(B) ![]()
(C) x is any real number
(D) x ![]() –1
–1
(E) x ![]() 1
1
2. The graph of ![]() is a
is a
(A) straight line
(B) line segment
(C) parabola
(D) portion of a parabola
(E) semicircle
3. Which of the following is (are) a pair of parametric equations that represent a circle?
I. ![]()
II. 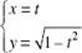
III. 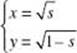
(A) only I
(B) only II
(C) only III
(D) only II and III
(E) I, II, and III