Answers and Explanations - Coordinate Geometry - Geometry and Measurement - REVIEW OF MAJOR TOPICS - SAT SUBJECT TEST MATH LEVEL 2

SAT SUBJECT TEST MATH LEVEL 2

PART 2

REVIEW OF MAJOR TOPICS

CHAPTER 2
Geometry and Measurement


2.1 Coordinate Geometry

Answers and Explanations

Transformations and Symmetry

1. (B) Horizontal translation (right) is accomplished by subtracting the amount of the translation (5) from x before the function is applied.

2. (D) Vertical stretching is accomplished by multiplying the function by the stretching factor after the function is applied.

3. (D) The graph of y = f (–x) – 2 reflects y = f (x) about the y-axis and translates it down 2.

4. (D) The horizontal shrinking by a factor of 2 is the multiplication of x by 2 before the function is applied. The reflection about the x -axis is the negation of the function after it is applied. The translation down 3 is the addition of –3 after the function is applied.

Conic Sections

1. (D) This is the standard equation of an ellipse with center (2, –1), a2 = 5, b2 = 4, and y -orientation. Since c2 = a2 – b2 = 1, the foci are 1 unit above and below the center.

2. (C) Complete the square in both x and y to put the equation in standard form:

  This hyperbola has x-orientation, with a2 = 4 and b2 = 3. Its asymptotes are .

3. (B) The directrix is a vertical line 4 units to the right of the focus. Therefore, the parabola has an x-orientation (the y-term is square). The vertex of (4, –3) is 2 units right of the focus, so p = –2.

4. (A) Since the vertices have the same y-coordinate, the major axis is horizontal, has length 8, and a2 = 16. Therefore, the center of the ellipse is (–1, 2). Since the minor axis has length 6, b2 = 9.

5. (D) Complete the square in both x and y to get the standard equation:

  The transverse axis has length 4, so the vertices of the hyperbola are 2 units left and right of the center (1, –3).

6. (C) Expand the right side of the equation and bring all but the constant term to the left side. Complete the square in both x and y to get 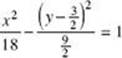, the standard equation of a hyperbola.

Polar Coordinates

1. (A) The angle must either be coterminal with (60 ± 360n) with r = 2 or (60 ± 180)° with r = –2. A is the only answer choice that meets these criteria.

2. * (A) With your calculator in degree mode, evaluate x = r cos = 2 cos 200 –1.88 and y = r sin 200 = 2 sin 200 –0.68.

3. * (D) With your graphing calculator in POLAR mode, enter as r1, and observe that the graph is a vertical line with holes where cos = 0.