SAT SUBJECT TEST MATH LEVEL 2
PART 2
![]()
REVIEW OF MAJOR TOPICS
![]()
CHAPTER 3
Numbers and Operations

3.1 Counting
![]()
Answers and Explanations
Venn Diagrams
1. (A) A Venn diagram will help you solve this problem.
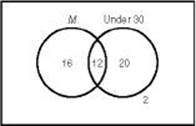
The two circles represent males and people who are at most 30 years of age, respectively. The part of the rectangle outside both circles represents people who are in neither category, i.e., females over the age of 30. First fill in the 12 males who are less than or equal to 30 years of age in the intersection of the circles. Since there are 28 males altogether, 16 are male and over 30. Since there are 32 people age 30 or less, there are 20 women that age. Add these together to get 48 people. Since there are 50 in the group, 2 must be women over 30.
Multiplication Rule
1. * (D) There are 6 choices of color for each of the three candies selected. Therefore, there are 6 × 6 × 6 = 216 color possibilities altogether.
2. * (E) The multiplication rule applies. There are (26)(26)(10)5 = 67,600,000 possible codes.
3. * (C) You can either include or exclude each of the seven ingredients in your salad, which means there are 2 choices for each ingredient. According to the multiplication rule, there are 27 = 128 ways of making these yes-no choices.
Factorial, Permutations, Combinations
1. * (C) This is the number of ways 3 objects can be chosen from 25, or ![]() = 25nCr3 = 2,300.
= 25nCr3 = 2,300.
2. * (B) There are ![]() ways of choosing the one center,
ways of choosing the one center, ![]() ways of choosing the two guards, and
ways of choosing the two guards, and ![]() ways of choosing the two forwards. Therefore, there are 5 × 36 × 78 = 14,040 possible starting teams.
ways of choosing the two forwards. Therefore, there are 5 × 36 × 78 = 14,040 possible starting teams.
3. * (C) There are ![]() ways of choosing 2 boys out of 5 and
ways of choosing 2 boys out of 5 and ![]() ways of choosing 2 girls out of 6. Therefore, there are 10 × 15 = 150 ways of choosing the homecoming court.
ways of choosing 2 girls out of 6. Therefore, there are 10 × 15 = 150 ways of choosing the homecoming court.
4. * (C) Since no three points are collinear, every pair of points determines a distinct line. There are ![]() such lines.
such lines.
5. (A) ![]() for any n.
for any n.