SAT SUBJECT TEST MATH LEVEL 2
PART 2
REVIEW OF MAJOR TOPICS
CHAPTER 1
Functions
1.2 Polynomial Functions
LINEAR FUNCTIONS
Linear functions are polynomials in which the largest exponent is 1. The graph is always a straight line. Although the general form of the equation is Ax + By + C = 0, where A, B, and C are constants, the most useful form occurs when the equation is solved for y. This is known as the slope-intercept form and is written y = mx + b. The slope of the line is represented by m and is defined to be the ratio of 
, where (x1, y1) and (x2, y2) are any two points on the line. The y-intercept is b (the point where the graph crosses the y-axis).
If you solve the general equation of a line, you will find that the slope is 
and the y-intercept is 
.
You can always quickly write an equation of a line when given its slope and a point on it by using the point-slope form: y – y1 = m(x – x1), where m is the slope and (x1,y1) is the point. If you are given two points on a line, you must first find the slope using the two points. Then use either point and this slope to write the equation. Once you have the equation in point-slope form, you can always solve for y to get the slope-intercept form if necessary.
EXAMPLES
1. Write an equation of the line containing (6,–5) and having slope 
.
In point-slope form, the equation is 
.
2. Write an equation of the line containing (1,–3) and (–4,–2).
First find the slope 
. Then use the point (1,–3) and this slope to write the point-slope equation 
.
Parallel lines have the same slope. The slopes of two perpendicular lines are negative reciprocals of one another.
3. The equation of line l1 is y = 2x + 3, and the equation of line l2 is y = 2x – 5.
These lines are parallel because the slope of each line is 2, and the y-intercepts are different.
4. The equation of line l1 is 
, and the equation of line l2 is 
.
These lines are perpendicular because the slope of l2,
, is the negative reciprocal of the slope of l1, 
You can use these facts to write an equation of a line that is parallel or perpendicular to a given line and that contains a given point.
5. Write an equation of the line containing (1,7) and parallel to the line 3x + 5y = 8.
The slope of the given line is 
. The point-slope equation of the line containing (1,7) is therefore 
.
6. Write an equation of the line containing (–3,2) and perpendicular to y = 4x – 5.
The slope of the given line is 4, so the slope of a line perpendicular to it is 
. The desired equation is 
.
The distance between two points P and Q whose coordinates are (x1,y1) and (x2,y2) is given by the formula
Distance = 
and the midpoint, M, of the segment 
has coordinates 
.
7. Given point (2,–3) and point (–5,4), find the length of 
and the coordinates of the midpoint, M.
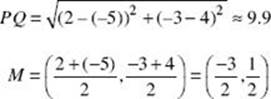
EXERCISES
1. The slope of the line through points A(3,–2) and B(–2,–3) is
(A) −5
(B) − 
(C)
(D) 1
(E) 5
2. The slope of line 8x + 12y + 5 = 0 is
(A) 
(B) 
(C) 
(D) 2
(E) 3
3. The slope of the line perpendicular to line 3x – 5y + 8 = 0 is
(A) 
(B) 
(C) 
(D) 
(E) 3
4. The y-intercept of the line through the two points whose coordinates are (5,–2) and (1,3) is
(A) 
(B) 
(C) 
(D) 7
(E) 17
5. The equation of the perpendicular bisector of the segment joining the points whose coordinates are (1,4) and (–2,3) is
(A) 3x – 2y + 5 = 0
(B) x – 3y + 2 = 0
(C) 3x + y – 2 = 0
(D) x – 3y + 11 = 0
(E) x + 3y – 10 = 0
6. The length of the segment joining the points with coordinates (–2,4) and (3,–5) is
(A) 2.8
(B) 3.7
(C) 10.0
(D) 10.3
(E) none of these
7. The slope of the line parallel to the line whose equation is 2x + 3y = 8 is
(A) –2
(B)
(C)
(D) 
(E) 
8. If the graph of 
is perpendicular to the graph of ax + 3y + 2 = 0, then a =
(A) – 4.5
(B) –2.22
(C) –1.35
(D) 0.45
(E) 1.35