SAT Math 1 & 2 Subject Tests
Chapter 13
Mathematics Level 1 Practice Test Form A
Click here to download a PDF of the Mathematics Level 1 Practice Test Form A.
![]()
MATHEMATICS LEVEL 1 TEST FORM A
For each of the following problems, decide which is the BEST of the choices given. If the exact numerical value is not one of the choices, select the choice that best approximates this value. Then fill in the corresponding oval on the answer sheet.
Notes: (1) A scientific or graphing calculator will be necessary for answering some (but not all) of the questions in this test. For each question, you will have to decide whether or not you should use a calculator.
(2) The only angle measure used on this test is degree measure. Make sure that your calculator is in degree mode.
(3) Figures that accompany problems on this test are intended to provide information useful in solving the problems. They are drawn as accurately as possible EXCEPT when it is stated in a specific problem that its figure is not drawn to scale. All figures lie in a plane unless otherwise indicated.
(4) Unless otherwise specified, the domain of any function f is assumed to be the set of all real numbers x for which f(x) is a real number. The range of f is assumed to be the set of all real numbers f(x), where x is in the domain of f.
(5) Reference information that may be useful in answering the questions on this test can be found below.
THE FOLLOWING INFORMATION IS FOR YOUR REFERENCE IN ANSWERING SOME OF THE QUESTIONS ON THIS TEST.
Volume of a right circular cone with radius r and height h: V = ![]() πr2 h
πr2 h
Lateral area of a right circular cone with circumference of the base c and slant height ℓ : S = ![]() cl
cl
Volume of a sphere with radius r: V = ![]() πr3
πr3
Surface area of a sphere with radius r: S = 4πr2
Volume of a pyramid with base area B and height h: V = ![]() Bh
Bh
1. If 34x = 81, then x =
(A) ![]()
(B) 1
(C) 3
(D) ![]()
(E) 9
2. If ![]() = 0.625, then
= 0.625, then ![]() is equal to which of the following?
is equal to which of the following?
(A) 1.60
(B) 2.67
(C) 2.70
(D) 3.33
(E) 4.25
3. If x − 3 = 3(1 − x), then what is the value of x ?
(A) 0.33
(B) 0.67
(C) 1.50
(D) 1.67
(E) 2.25
4. Points A, B, C, and D are arranged on a line in that order. If AC = 13, BD = 14, and AD = 21, then BC =
(A) 12
(B) 9
(C) 8
(D) 6
(E) 3
5. The distance between the points (−3, 5) and (−3, −12) is
(A) ![]()
(B) 7
(C) 9
(D) 17
(E) ![]()
6. At what coordinates does the graph of 3y + 5 = x − 1 intersect the y-axis?
(A) (0, −2)
(B) (0, −1)
(C) ![]()
(D) (−2, 0)
(E) (−6, 0)
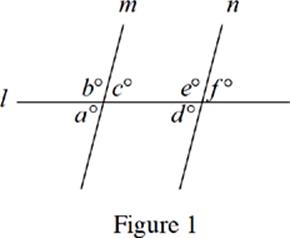
7. In Figure 1, if m![]() n and b = 125, then d + f =
n and b = 125, then d + f =
(A) 50°
(B) 55°
(C) 110°
(D) 130°
(E) 180°
8. If the cube root of the square root of a number is 2, what is the number?
(A) 16
(B) 64
(C) 128
(D) 256
(E) 1,024
9. If 7a + 2b = 11 and a − 2b = 5, then what is the value of a ?
(A) −2.0
(B) −1.5
(C) −0.5
(D) 1.4
(E) 2.0
10. If f(x) = x2 − 3x, then f(−3) =
(A) 0
(B) 3.3
(C) 6.0
(D) 9.9
(E) 18.0
11. Which of the following could be the graph of |y ≥ 3?
(A) 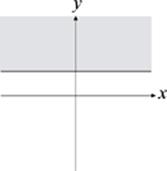
(B) 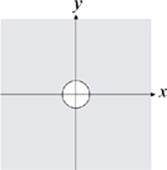
(C) 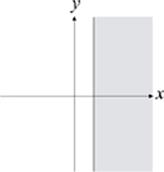
(D) 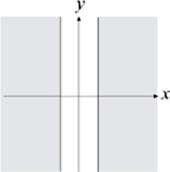
(E) 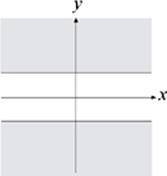
12. If m varies directly as n and ![]() = 5, then what is the value of m when n = 2.2 ?
= 5, then what is the value of m when n = 2.2 ?
(A) 0.44
(B) 2.27
(C) 4.10
(D) 8.20
(E) 11.00
13. What is the slope of the line given by the equation 3y − 5 = 7 − 2x ?
(A) −2
(B) −![]()
(C) ![]()
(D) 2
(E) 6
14. 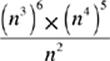
(A) n9
(B) n16
(C) n19
(D) n36
(E) n40
15. If f(x) = 5 − 2x and g(x) = x2 + 7, then f(g(2)) =
(A) −17
(B) −8
(C) 8
(D) 17
(E) 24
16. Students in a certain research program are either engineers or doctoral candidates; some students graduate each year. In a certain year, no doctoral candidates graduate. Which of the following statements must be true?
(A) The program then contains more engineers than doctoral candidates.
(B) Doctoral candidates are poorer students than engineers.
(C) More doctoral candidates will graduate in following years.
(D) Every student graduating in that year is an engineer.
(E) All engineers in the program graduate in that year.
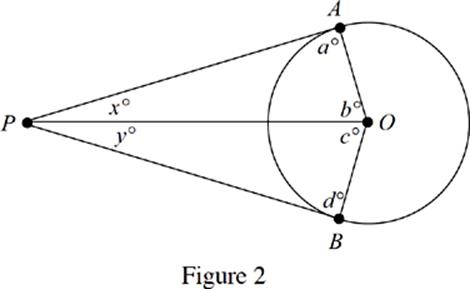
17. In Figure 2, if segments PA and PB are tangent to the circle with center O at A and B, respectively, then which of the following must be true?
I. PB > PO
II. x = y
III. x + y + b + c = a + d
(A) I only
(B) II only
(C) I and II only
(D) II and III only
(E) I, II, and III
18. Rodney is starting a small business selling pumpkins. If he spends $200 on supplies and sells his pumpkins for $4 each, which of the following functions correctly shows the amount of money Rodney has gained or lost when he has sold x pumpkins?
(A) f(x) = 800x
(B) f(x) = 200x + 4
(C) f(x) = 200x − 4
(D) f(x) = 4x + 200
(E) f(x) = 4x − 200
19. If the perimeter of a square is 60, what is the area of the square?
(A) 15![]()
(B) 20![]()
(C) 80
(D) 150
(E) 225
20. If 0 < n < 1, then all of the following must be true EXCEPT
(A) n2 < n
(B) n < ![]()
(C) |n| < n
(D) −n < n
(E) n < ![]()
21. Which of the following lines is perpendicular to the line 3x − 2y = 16 ?
(A) 3x − 2y = 25
(B) 3x + 2y = 16
(C) 2x − 3y = 7
(D) 6x + 9y = 16
(E) 6x − 9y = 32
22. Where defined, 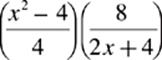 =
=
(A) 1
(B) x
(C) x − 2
(D) x + 2
(E) 2x2 − 8
23. The surface area of a sphere is 75 square centimeters. What is the volume of the sphere, in cubic centimeters?
(A) 2.443
(B) 5.968
(C) 14.581
(D) 18.75
(E) 61.075
24. If ∠A and ∠B are acute angles, then ∠A and ∠B CANNOT be
(A) vertical angles
(B) complementary angles
(C) supplementary angles
(D) congruent angles
(E) adjacent angles
25. If i2 = −1, then 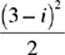
(A) 3 − 2i
(B) 4 − 3i
(C) 7 + 2i
(D) 8 − 6i
(E) 9 + 6i
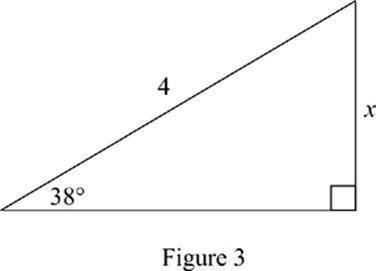
26. In Figure 3, what is the value of x ?
(A) 0.62
(B) 0.79
(C) 2.46
(D) 3.13
(E) 3.15
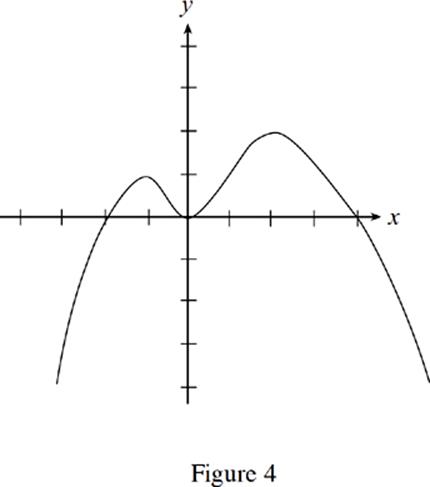
27. If Figure 4 shows part of the graph of y = f(x), then which of the following could be the range of f(x) ?
(A) {y: y ≤ 2}
(B) {y: y = −2, 3}
(C) {y: y = 1, 2}
(D) {y: −2 ≤ y ≤ 3}
(E) {y: 1 ≤ y ≤ 2}
28. Joan and Grant are shopping at the deli for lunchmeat. If Joan buys 3 pounds of bologna for $2.80 per pound, and Grant buys 2 pounds of pastrami for $1.80 per pound, then what is the average (arithmetic mean) price per pound of all the lunchmeat they buy?
(A) $2.30
(B) $2.40
(C) $3.60
(D) $4.60
(E) $8.40
29. If a cube and a sphere intersect at exactly eight points, then which of the following must be true?
(A) The sphere is inscribed in the cube.
(B) The cube is inscribed in the sphere.
(C) The diameter of the sphere is equal in length to an edge of the cube.
(D) The sphere and the cube have equal volumes.
(E) The sphere and the cube have equal surface areas.
30. If Set S consists of ten distinct positive integers, which of the following could be a member of S ?
I. The mean of the members of S
II. The median of the members of S
III. The mode of the members of S
(A) None
(B) I only
(C) II only
(D) I and III
(E) II and III
31. If f(x) = 2x2 + 2, then what is the value of f(x + 4) ?
(A) 2x2 + 4
(B) 2x2 + 6
(C) 2x2 + x + 6
(D) 2x2 + 16x + 32
(E) 2x2 + 16x + 34
32. If 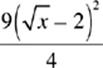 = 6.25, then x could equal which of the following?
= 6.25, then x could equal which of the following?
(A) 0.11
(B) 2.42
(C) 9.00
(D) 10.24
(E) 13.76
33. If 0° < θ < 90°, then 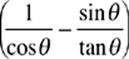 (cos °) =
(cos °) =
(A) cos θ
(B) sin θ
(C) tan θ
(D) sin2 θ
(E) tan2 θ
34. If f(x) = 2x5, then which of the following must be true?
I. f(x) = f(−x)
II. f(−x) = −f(x)
III. ![]() f(x) = f(
f(x) = f(![]() x)
x)
(A) I only
(B) II only
(C) I and III only
(D) II and III only
(E) I, II, and III
35. What is the domain of f(x) = 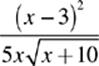 ?
?
(A) All real numbers
(B) All real numbers less than 2
(C) All real numbers between −10 and 0
(D) All real numbers greater than −7
(E) All real numbers greater than −10 except 0
36. How many distinct 3-digit numbers contain only nonzero digits?
(A) 909
(B) 899
(C) 789
(D) 729
(E) 504
37. At what points does the circle given by the equation (y − 3)2 + (x − 2)2 = 16 intersect the y-axis?
(A) (0, −5.66) and (0, 5.66)
(B) (0, −0.46) and (0, 6.46)
(C) (0, −1.00) and (0, 7.00)
(D) (−0.65, 0) and (4.65, 0)
(E) (−2.00, 0) and (6.00, 0)
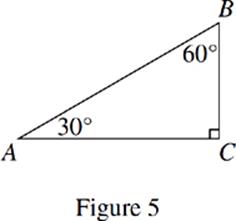
38. In Figure 5, ∠ABC can be rotated around either leg to form a cone. Which of the following could be the ratio of the volumes of these cones?
(A) |n| : 1
(B) 2 : 1
(C) 3 : 1
(D) 4 : 1
(E) 9 : 1
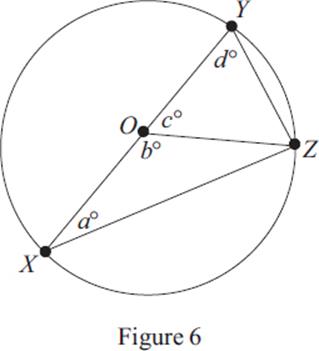
39. In Figure 6, in the circle with center O, which of the following is equal to c ?
(A) ![]()
(B) d
(C) 2a
(D) ![]()
(E) b − 90
40. A researcher finds that an ant colony”s population increases by exactly 8% each month. If the colony has an initial population of 1,250 insects, which of the following is the nearest approximation of the population of the colony 2 years later?
(A) 7,926
(B) 5,832
(C) 3,650
(D) 2,400
(E) 1,458
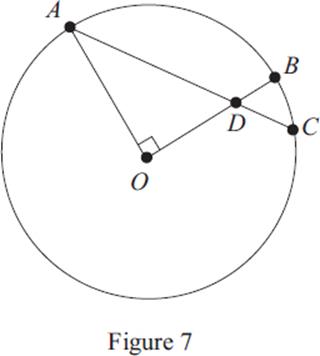
41. In Figure 7, if the circle with center O has a radius of 4 and OD = 3DB, then sin ∠A =
(A) 0.60
(B) 0.71
(C) 0.80
(D) 0.87
(E) 1.00
42. Which of the following represents the solution set of |x3 − 8|? ≤ 5
(A) −1.71 ≤ x ≤ 1.71
(B) 0 ≤ x ≤ 3.21
(C) 0.29 ≤ x ≤ 3.71
(D) 1.44 ≤ x ≤ 2.35
(E) 6.29 ≤ x ≤ 9.71
43. Six congruent circles are arranged so that each circle is externally tangent to at least two other circles. The centers of these six circles are then connected to form a polygon. If each circle has a radius of 2, then what is the perimeter of this polygon?
(A) 6
(B) 12
(C) 24
(D) 36
(E) 48
44. What is the distance between the x-intercept and the y-intercept of the line given by the equation 2y = 6 − x ?
(A) 3.67
(B) 6.32
(C) 6.71
(D) 7.29
(E) 8.04
45. The point (5, −10) is at a distance of 26 from point Q, and the point (2, −10) is at a distance of 25 from Q. Which of the following could be the coordinates of Q ?
(A) (−5, 14)
(B) (−3, 18)
(C) (−1, 19)
(D) (0, 21)
(E) (2, 16)
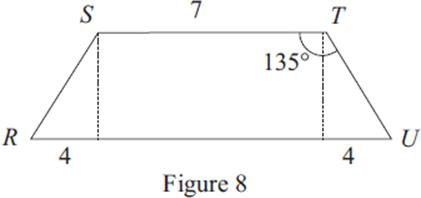
Note: Figure not drawn to scale.
46. In Figure 8, what is the area of isosceles trapezoid RSTU ?
(A) 12
(B) 18
(C) 24
(D) 44
(E) 56
47. Which of the following has the greatest value?
(A) 1.73999
(B) 2799
(C) 3500
(D) 4400
(E) 250100
48. If f(x) = 4x2 + 4x + 4, which of the following is equal to f(−3.5) ?
(A) f(−14)
(B) f(−7)
(C) f(−0.5)
(D) f(0.5)
(E) f(2.5)
49. A fair cube is one that is labeled with the numbers 1, 2, 3, 4, 5, and 6, such that there is an equal probability of rolling each of those numbers. If Jade rolls two fair cubes at the same time, then what is the probability that the product of the two numbers she rolls will be greater than 18 ?
(A) 0.222
(B) 0.278
(C) 0.5
(D) 0.6
(E) 0.778
50. If z = logx (yx), then xz =
(A) xx
(B) yx
(C) xyx
(D) y2x
(E) x2y
S T O P
IF YOU FINISH BEFORE TIME IS CALLED, YOU MAY CHECK YOUR WORK ON THIS TEST ONLY. DO NOT WORK ON ANY OTHER TEST IN THIS BOOK.
HOW TO SCORE THE PRINCETON REVIEW PRACTICE SAT MATH SUBJECT TEST
When you take the real exam, the proctors will collect your test booklet and bubble sheet and send your bubble sheet to New Jersey where a computer looks at the pattern of filled-in ovals on your bubble sheet and gives you a score. We couldn”t include even a small computer with this book, so we are providing this more primitive way of scoring your exam.
Determining Your Score
STEP 1 Using the answers on the next page, determine how many questions you got right and how many you got wrong on the test. Remember: Questions that you do not answer don”t count as either right answers or wrong answers.
STEP 2 List the number of right answers here.
STEP 3 List the number of wrong answers here. Now divide that number by 4. (Use a calculator if you”re feeling particularly lazy.)
STEP 4 Subtract the number of wrong answers divided by 4 from the number of correct answers. Round this score to the nearest whole number. This is your raw score.
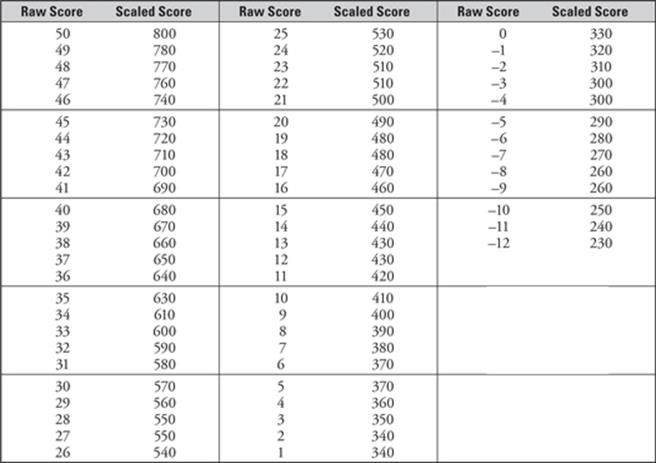
STEP 5 To determine your real score, take the number from Step 4 above and look it up in the left column of the Score Conversion Table on this page; the corresponding score on the right is your score on the exam.
(A) ______________
(B) ______________ ÷ 4 = (C)______________
(A) ______________ − (C) ______________ = ______________
MATHEMATICS LEVEL 1 SUBJECT TEST FORM A
Answer Key
1. B
2. A
3. C
4. D
5. D
6. A
7. C
8. B
9. E
10. E
11. E
12. E
13. B
14. D
15. A
16. D
17. D
18. E
19. E
20. C
21. D
22. C
23. E
24. C
25. B
26. C
27. A
28. B
29. B
30. B
31. E
32. A
33. D
34. B
35. E
36. D
37. B
38. A
39. C
40. A
41. A
42. D
43. C
44. C
45. A
46. D
47. D
48. E
49. A
50. B
MATHEMATICS SUBJECT TEST SCORE CONVERSION TABLE