SAT Math 1 & 2 Subject Tests
Chapter 14
Mathematics Level 1 Practice Test Form B
Click here to download a PDF of the Mathematics Level 1 Practice Test Form B.
![]()
MATHEMATICS LEVEL 1 TEST FORM B
For each of the following problems, decide which is the BEST of the choices given. If the exact numerical value is not one of the choices, select the choice that best approximates this value. Then fill in the corresponding oval on the answer sheet.
Notes: (1) A scientific or graphing calculator will be necessary for answering some (but not all) of the questions on this test. For each question, you will have to decide whether or not you should use a calculator.
(2) The only angle measure used on this test is degree measure. Make sure that your calculator is in degree mode.
(3) Figures that accompany problems on this test are intended to provide information useful in solving the problems. They are drawn as accurately as possible EXCEPT when it is stated in a specific problem that its figure is not drawn to scale. All figures lie in a plane unless otherwise indicated.
(4) Unless otherwise specified, the domain of any function f is assumed to be the set of all real numbers x for which f(x) is a real number. The range of f is assumed to be the set of all real numbers f(x), where x is in the domain of f.
(5) Reference information that may be useful in answering the questions on this test can be found below.
THE FOLLOWING INFORMATION IS FOR YOUR REFERENCE IN ANSWERING SOME OF THE QUESTIONS ON THIS TEST.
Volume of a right circular cone with radius r and height h: V = ![]() πr2 h
πr2 h
Lateral area of a right circular cone with circumference of the base c and slant height ℓ: S = ![]() cl
cl
Volume of a sphere with radius r: V = ![]() πr3
πr3
Surface area of a sphere with radius r: S = 4πr2
Volume of a pyramid with base area B and height h: V = ![]() Bh
Bh
1. Rob and Sherry together weigh 300 pounds. Sherry and Heather together weigh 240 pounds. If all three people together weigh 410 pounds, then what is Sherry”s weight in pounds?
(A) 110
(B) 115
(C) 120
(D) 130
(E) 145
2. If the point (5, 2) is reflected across the x-axis, then what are the coordinates of the resulting point?
(A) (5, 0)
(B) (0, 2)
(C) (5, −2)
(D) (−5, 2)
(E) (2, 5)
3. If r = ![]() and s = 6, then
and s = 6, then ![]() +
+ ![]() =
=
(A) 4
(B) 6
(C) 9
(D) 12
(E) 18
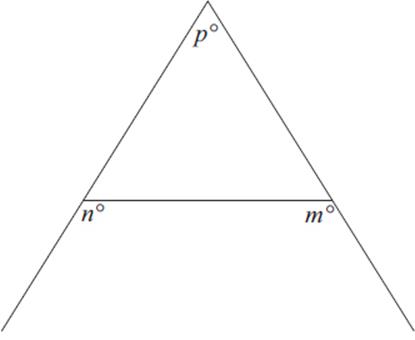
Figure 1
4. In Figure 1, what is the value of p in terms of m and n ?
(A) m + n − 180
(B) m + n + 180
(C) m − n + 360
(D) 360 − (m − n)
(E) 360 − (m + n)
5. After 8:00 p.m., a ride in a taxi costs $2.50 plus $0.30 for every fifth of a mile traveled. If a passenger travels b miles, then what is the cost of the trip, in dollars, in terms of b ?
(A) 2.5 + 0.3b
(B) 2.5 + 1.5b
(C) 2.8b
(D) 30 + 250b
(E) 250 + 30b
6. If |y − 3| = 4y − 7, then which of the following could be the value of y ?
(A) ![]()
(B) 1
(C) ![]()
(D) 2
(E) 5
7. What is the slope of the line given by the equation y + 3 = ![]() (x − 7) ?
(x − 7) ?
(A) −![]()
(B) −![]()
(C) ![]()
(D) ![]()
(E) ![]()
8. If a = cos θ and b = sin θ, then for all θ, a2 + b2 =
(A) 0
(B) 1
(C) 2
(D) (cos θ + sin θ)2
(E) (cos θ • sin θ)2
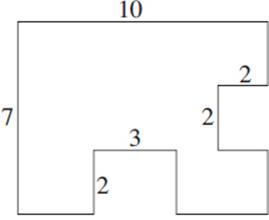
Figure 2
9. In Figure 2, if every angle in the polygon is a right angle, then what is the perimeter of the polygon?
(A) 34
(B) 42
(C) 47
(D) 52
(E) 60
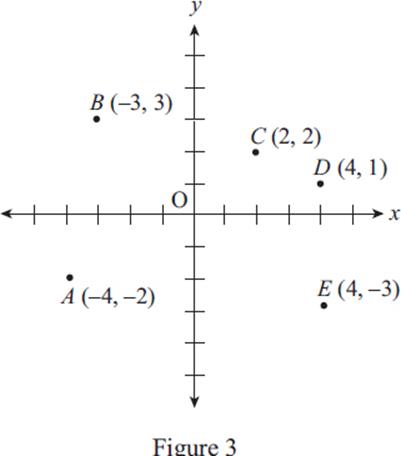
Figure 3
10. For which of the points shown in Figure 3 is |x + y| > 5 ?
(A) A
(B) B
(C) C
(D) D
(E) E
Questions 11-12 refer to the chart below, which shows the monthly sales made by a salesperson in 1996.
Keri”s Monthly Sales for 1996
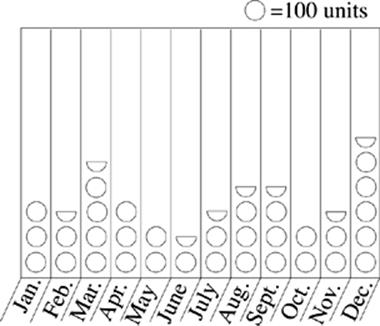
11. As a saleswoman, Keri receives a $10.00 commission for each unit she sells. In any month in which she sells more than 300 units, she receives an additional bonus of $1,000.00. What was the total amount Keri received in bonuses in 1996 ?
(A) $3,000.00
(B) $4,000.00
(C) $5,000.00
(D) $6,000.00
(E) $8,000.00
12. In 1996, Keri had the greatest total income from commissions and bonuses in what three-month period?
(A) January, February, March
(B) February, March, April
(C) March, April, May
(D) July, August, September
(E) October, November, December
13. If a varies directly as b2, and a = 14 when b = 2, then what is the value of a when b = 5 ?
(A) 3.6
(B) 14
(C) 35
(D) 70
(E) 87.5
14. If ![]() =
= ![]() , then
, then ![]() =
=
(A) 0.27
(B) 0.33
(C) 0.42
(D) 0.66
(E) 1.25
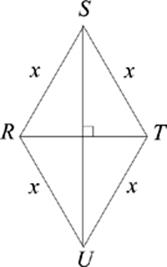
Figure 4
15. In Figure 4, sin ∠RSU must be equal to which of the following?
(A) cos ∠RTU
(B) cos ∠TSU
(C) sin ∠SRT
(D) sin ∠STR
(E) sin ∠TRU
16. If y = ![]() +
+ ![]() , then which of the following statements must be true?
, then which of the following statements must be true?
I. x > 1
II. x ≠ 3
III. x ≠ −3
(A) I only
(B) II only
(C) I and III only
(D) II and III only
(E) I, II, and III
17. Sphere O is inscribed in cube A, and cube B is inscribed in sphere O. Which of the following quantities must be equal?
(A) An edge of A and the radius of O
(B) The diameter of O and the longest diagonal in A
(C) An edge of B and the diameter of O
(D) An edge of B and the radius of O
(E) An edge of A and the longest diagonal in B
18. If a − x = 12, b − y = 7, c − z = 15, and a + b + c = 50, then x + y + z =
(A) 16
(B) 18
(C) 34
(D) 66
(E) 84
19. A jeep has four seats, including one driver”s seat and three passenger seats. If Amber, Bunny, Cassie, and Donna are going for a drive in the jeep, and only Cassie can drive, then how many different seating arrangements are possible?
(A) 3
(B) 6
(C) 12
(D) 16
(E) 24
20. If ![]() x − 3 = 2
x − 3 = 2 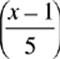 , then x =
, then x =
(A) 9
(B) 11
(C) 13
(D) 22
(E) 26
21. Line l passes through the origin and point (a, b). If ab ≠ 0 and line l has a slope greater than 1, then which of the following must be true?
(A) a = b
(B) a > b
(C) a2 < b2
(D) b − a < 0
(E) a + b > 0
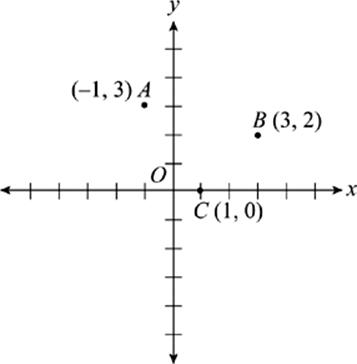
Figure 5
22. In Figure 5, points A, B, and C are three vertices of a parallelogram, and point D (not shown) is the fourth vertex. How many points could be D ?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
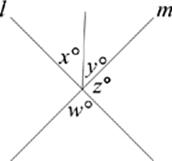
Figure 6
Note: Figure not drawn to scale.
23. In Figure 6, lines l and m intersect as shown. If y = ![]() x and w = 2z, then x =
x and w = 2z, then x =
(A) 30
(B) 40
(C) 48
(D) 60
(E) 72
24. Circle O has a radius of r. If this radius is increased by t, then which of the following correctly expresses the new area of circle O ?
(A) πt2
(B) 2π(r + t)
(C) π(t2 + r2)
(D) π(r2 + 2rt + t2)
(E) 4π(r2 + 2rt + t2)
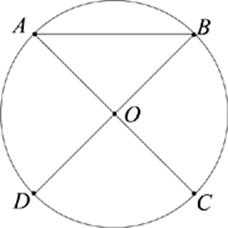
Figure 7
25. In Figure 7, AC and BD are perpendicular diameters of the circle with center O. If the circle has an area of 9π, what is the length of AB ?
(A) 2.12
(B) 3.36
(C) 4.24
(D) 6.36
(E) 8.48
26. If x < |x| and x2 + 2x − 3 = 0, then 2x + 4 =
(A) −2
(B) 2
(C) 6
(D) 8
(E) 10
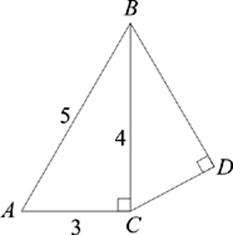
Figure 8
27. In Figure 8, triangles ABC and CBD are similar. What is the area of triangle CBD ?
(A) 3.07
(B) 3.84
(C) 5.24
(D) 7.68
(E) 9.60
28. If i = ![]() , then (5 − 3i)(4 + 2i) =
, then (5 − 3i)(4 + 2i) =
(A) 14 − 2i
(B) 16
(C) 24
(D) 26 − 2i
(E) 28
29. If f(x) = x2 − 5x and f(n) = −4, then which of the following could be the value of n ?
(A) −5
(B) −4
(C) −1
(D) 1
(E) 5
30. Two identical rectangular solids, each of dimensions 3 × 4 × 5, are joined face to face to form a single rectangular solid with a length of 8. What is the length of the longest line segment that can be drawn within this new solid?
(A) 8.60
(B) 9.90
(C) 10.95
(D) 11.40
(E) 12.25
31. Which of the following most closely approximates (5.5 × 104)2 ?
(A) 3.0 × 105
(B) 3.0 × 106
(C) 3.0 × 107
(D) 3.0 × 108
(E) 3.0 × 109
|
x |
P(x) |
|
0 |
|
|
1 |
|
|
2 |
n |
|
3 |
|
|
4 |
|
32. If a fair coin is flipped four times, the probability of the coin landing heads-side-up x times is shown in the table above. What is the value of n ?
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
33. A sample of metal is heated to 698°C and then allowed to cool. The temperature of the metal over time is given by the formula n = 698 − 2t − 0.5t2, where t is the time in seconds after the start of the cooling process, and n is the temperature of the sample in degrees Celsius. After how many seconds will the temperature of the sample be 500°C ?
(A) 16
(B) 18
(C) 20
(D) 22
(E) 24
34. Perpendicular lines l and m intersect at (4, 5). If line m has a slope of −![]() , which of the following is an equation for line l ?
, which of the following is an equation for line l ?
(A) y = ![]() x − 1
x − 1
(B) y = ![]() x + 3
x + 3
(C) y = ![]() x + 5
x + 5
(D) y = 2x − 1
(E) y = 2x − 3

Figure 9
35. In Figure 9, points A, B, C, and D are all on the circle with center O. If ∠BDA measures 25°, and ∠CAD measures 32°, what is the measure of ∠BOC in degrees?
(A) 33
(B) 66
(C) 123
(D) 147
(E) 303
36. If 4x + 2 = 48, then 4x =
(A) 3.0
(B) 6.4
(C) 6.9
(D) 12.0
(E) 24.0
37. If r(x) = 6x + 5 and s(r(x)) = 2x − 1, then s(x) =
(A) −4x − 6
(B) ![]()
(C) ![]()
(D) 3x − 6
(E) 4x + 4
38. Of the 850 stores in Noel-Bentley County, 250 have alarm systems and 450 have guard dogs. If 350 stores have neither alarm systems nor guard dogs, then how many stores have both alarm systems and guard dogs?
(A) 100
(B) 150
(C) 200
(D) 500
(E) 700
39. If log9 27 = n, then n =
(A) ![]()
(B) 1
(C) ![]()
(D) ![]()
(E) 3
40. A cylindrical cup has a height of 3 inches and a radius of 2 inches. How many such cups may be completely filled from a full rectangular tank whose dimensions are 6 × 7 ×8 inches?
(A) 8
(B) 9
(C) 12
(D) 17
(E) 28
41. Line segments AC and BD intersect at point O, such that each segment is the perpendicular bisector of the other. If AC = 7 and BD = 6, then sin ∠ADO =
(A) 0.16
(B) 0.24
(C) 0.39
(D) 0.76
(E) 0.85
42. Which of the following boxplots represents the data set with the greatest interquartile range?
(A) 
(B) 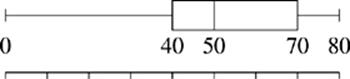
(C) 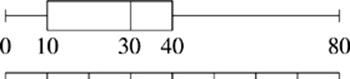
(D) 
(E) 
43. If f(x) = kx, where k is a nonzero constant, and g(x) = x + k, then which of the following statements must be true?
I. f(2x) = 2f(x)
II. f(x + 2) = f(x) + 2
III. f(g(x)) = g(f(x))
(A) I only
(B) II only
(C) I and II only
(D) I and III only
(E) I, II, and III
44. A rectangular room has walls facing due north, south, east, and west. On the southern wall, a tack is located 85 inches from the floor and 38 inches from the western wall, and a nail is located 48 inches from the floor and 54 inches from the western wall. What is the distance in inches between the tack and the nail?
(A) 21.0
(B) 26.4
(C) 32.6
(D) 37.0
(E) 40.3
45. If f(x) = ![]() , then which of the following is the domain of f ?
, then which of the following is the domain of f ?
(A) {x: x ≠ ![]() }
}
(B) {x: x ≥ 0}
(C) {x: −![]() ≥ x ≥
≥ x ≥ ![]() }
}
(D) {x: 0 > x > ![]() }
}
(E) {x: 0 ≤ x ≤ 144}
“If a tree falls in the forest,
a sound is heard.”
46. If the statement above is true, then which of the following CANNOT be true?
(A) No tree falls in the forest, but a sound is heard.
(B) No sound is heard as a tree falls in the forest.
(C) A sound is heard as a tree falls in the forest.
(D) No tree falls in the forest, and no sound is made.
(E) A sound is heard in the forest as no tree falls.
47. At a dance competition, each of six couples must compete against the other five couples in a dance-off three times before the winning couple can be declared. How many such dance-offs will occur?
(A) 12
(B) 33
(C) 45
(D) 60
(E) 63
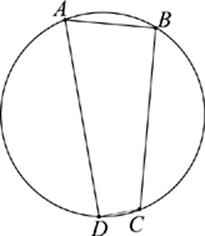
Figure 10
Note: Figure not drawn to scale.
48. In Figure 10, AB = 4, BC = 7, and CD = 1.
If AC is a diameter of the circle, then what is the length of AD ?
(A) 3
(B) 6
(C) 8
(D) ![]()
(E) 10
49. (0, 0) and (−2, 2) are the coordinates of two vertices of an equilateral triangle. Which of the following could be the coordinates of the third vertex?
(A) (−2.0, 0)
(B) (−0.73, 2.73)
(C) (−0.73, 0.73)
(D) (0, 2.0)
(E) (0.73, 2.73)
50. What is the distance between the two x-intercepts of the graph of y = x2 − 9x + 19.25 ?
(A) 2.0
(B) 3.5
(C) 5.5
(D) 10.25
(E) 28.25
S T O P
IF YOU FINISH BEFORE TIME IS CALLED, YOU MAY CHECK YOUR WORK ON THIS TEST ONLY. DO NOT WORK ON ANY OTHER TEST IN THIS BOOK.
HOW TO SCORE THE PRINCETON REVIEW PRACTICE SAT MATH SUBJECT TEST
When you take the real exam, the proctors will collect your test booklet and bubble sheet and send your bubble sheet to New Jersey where a computer looks at the pattern of filled-in ovals on your bubble sheet and gives you a score. We couldn”t include even a small computer with this book, so we are providing this more primitive way of scoring your exam.
Determining Your Score
STEP 1 Using the answers on the next page, determine how many questions you got right and how many you got wrong on the test. Remember: Questions that you do not answer don”t count as either right answers or wrong answers.
STEP 2 List the number of right answers here.
STEP 3 List the number of wrong answers here. Now divide that number by 4. (Use a calculator if you”re feeling particularly lazy.)
STEP 4 Subtract the number of wrong answers divided by 4 from the number of correct answers. Round this score to the nearest whole number. This is your raw score.
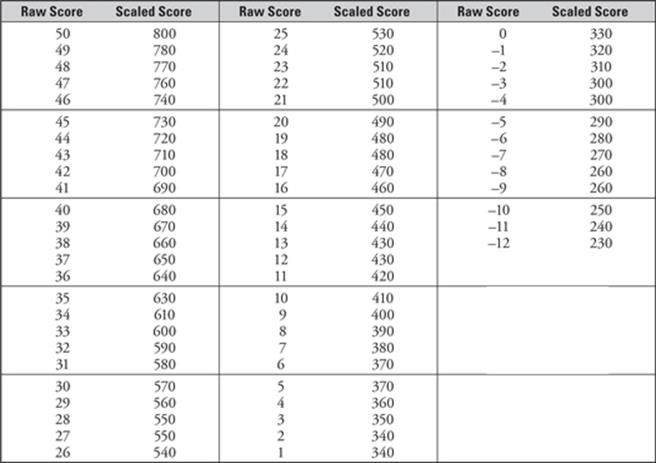
STEP 5 To determine your real score, take the number from Step 4 above and look it up in the left column of the Score Conversion Table on this page; the corresponding score on the right is your score on the exam.
(A) ______________
(B) ______________ ÷ 4 = (C)______________
(A) ______________ − (C) ______________ = ______________
MATHEMATICS LEVEL 1 SUBJECT TEST FORM B
Answer Key
1. D
2. C
3. E
4. A
5. B
6. D
7. E
8. B
9. B
10. A
11. B
12. D
13. E
14. C
15. A
16. D
17. E
18. A
19. B
20. E
21. C
22. C
23. E
24. D
25. C
26. A
27. B
28. D
29. D
30. B
31. E
32. D
33. B
34. E
35. B
36. A
37. C
38. C
39. C
40. A
41. D
42. A
43. A
44. E
45. C
46. B
47. C
48. C
49. E
50. A
MATHEMATICS SUBJECT TEST SCORE CONVERSION TABLE