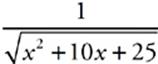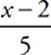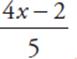Functions - SAT Math 1 & 2 Subject Tests

SAT Math 1 & 2 Subject Tests

Chapter 9 Functions

ETS will test you on two types of functions. One type is what they call “algebraic functions.” They use a funny symbol to represent a series of algebraic operations. Here are a couple of examples:

These are generally testing your basic math skills, everything from vocabulary to PEMDAS. Functions sometimes do show up in this form on the Math Subject Tests—especially the Math Level 1—but you”re likely to encounter more functions in mathematical notation, like this:

Functions in f(x) notation should be treated just like functions with funny symbols. When dealing with functions in the f(x) form, however, you can expect to need a few other rules as well—rules relating to the properties of functions and their graphs. This chapter will take you through what you need to know.

Definitions

Here are some terms concerning algebraic functions that appear on the Math Subject Tests. Make sure you”re familiar with them. If the meaning of any of these vocabulary words keeps slipping your mind, add that word to your flash cards.

Domain	The set of values that may be put into a function.
Range	The set of values that can be produced by a function.
Even Function	A function for which f(x) = f(−x)—even functions are symmetrical across the y-axis.
Odd Function	A function for which −f(x) = f(−x)—odd functions have origin symmetry, which means that they are the same when reflected across the origin.
Root	Values in a function”s domain at which the function equals zero—a root is also called a zero, solution, or x-intercept of a function.
Degree	The sum of the exponents in an algebraic term—the degree of a polynomial is the highest degree of any term in the polynomial.
Asymptote	A line that the graph of a function approaches but never reaches.
Period	In periodic functions, the distance traveled by the function before it repeats itself.
Frequency	The number of times a graph repeats itself in a given distance; the reciprocal of the function”s period.
Amplitude	In a periodic function, the distance that the graph rises above a central value.
Nonnegative	The values of a function that are greater than or equal to zero.

$&#*@! FUNCTIONS

These are the functions with the funny symbols. ETS will try to frighten you with weird characters, but as long as you can follow the directions and Plug In, you”ll have little trouble with these questions.

13. If ◊a◊ = a² − 5a + 4, then ◊6◊ =

(A) 6

(B) 8

(D) 12

(E) 14

Here”s How to Crack It

Answer this question by plugging 6 into the definition of the function everywhere a is found.

(6)² − 5(6) + 4 =

36 − 30 + 4 =

The answer is (C).

Don”t be confused if a question requires you to plug something strange into a function. Just follow the instructions, and the answer will become clear.

17. If &y = y² − 6, then which of the following equals &(y + 6) ?

(A) y²

(B) y² − 36

(D) y² + 12y + 30

(E) y² + 12y + 42

Here”s How to Crack It

To find the answer, just Plug In a number. Let”s pick y = 2.

That means we want to find the value of &(2 + 6), which is &8. Plugging 8 into the definition gives us

(8)² − 6 = 58

Now just Plug In 2 for y in the answer choices to see which one becomes 58, your target number. (D) is the correct answer.

DRILL

Practice your techniques on the following function questions. The answers to these drills can be found in Chapter 12.

34. If [x] = −|x³|, then [4] − [3] =

(A) −91

(B) −37

(D) 37

(E) 91

35. If ¥c is defined as 5(c − 2)², then ¥5 + ¥6 =

(A) ¥7

(B) ¥8

(D) ¥10

(E) ¥11

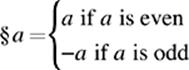
36. §1 + §2 + §3 … §100 + §101 =

(A) −151

(B) −51

(D) 50

(E) 51

FUNCTIONS WITHOUT WEIRD SYMBOLS

On many questions, ETS will also give you functions with letters like f and g, that look like the ones you”ve probably studied in school. A function is a type of relation between two sets of numbers called the domain and range of the function. Specifically, a function is a relation in which every element in the domain corresponds to only one element in the range; for every x in the function, there is only one possible f(x) (or y, on a graph).

The most basic function questions test only your understanding of functions and the algebra required to work with them. Here are some examples of basic functions.

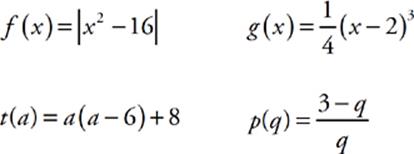
The best way to think of function is that it”s like a machine. It spits out a different result depending on what you put into it. As long as you follow the directions of the machine, it will spit out the right response for you. The test may bring up a couple of phrases: independent variable and dependent variable. The independent variable is what you put into the machine. You could put anything in; it doesn”t rely on anything, so it”s independent. The dependent variable is what your machine spits out. What it is depends on what”s put into the machine. That”s why it”s thedependent variable. On a graph, the independent variable is on the x-axis and the dependent variable is on the y-axis.

f(x) = y

Sometimes it helps to
think of f(x) as being equal
to y. Both are the result
you get when you put a
number into the equation.

When questions ask you to work with algebraic functions, you”ll be required to do one of two things: plug numbers into a function and get a numerical answer, or plug variables into a function and get an algebraic answer. For example, given the function g(x) = (x + 2)², you could run into two types of questions:

The Rare Occasion

There are a few unusual function types that you should be prepared for. It is possible, for example, for elements in the domain to consist of more than one value, like this:

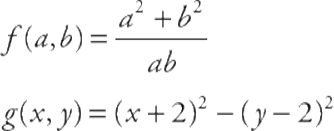
In each of these functions, an element in the domain is a pair of values. Functions of this kind are fairly rare on the Math Subject Tests, but you may run into one. Although they”re unusual, they”re not difficult. Simply treat them like ordinary functions—to calculate the value of f(3,4), for example, simply take the values 3 and 4 and plug them into the definition of the function in the positions of a and b, respectively (you get ).

3. If g(x) = (x + 2)², what is the value of g(4) ?

(A) 8

(B) 12

(D) 36

(E) 64

Here”s How to Crack It

Answering this question is a simple matter of plugging 4 into the function, and simplifying (4 + 2)² to get 36.

Here, on the other hand, is an algebraic version of the same question:

18. If g(x) = (x + 2)², what is the value of g(x + 2) ?

(A) x² + 4

(B) x² + 6

(D) x² + 4x + 6

(E) x² + 8x + 16

Here”s How to Crack It

To solve this question, just Plug In a number for x. Let”s pick x = 3, and plug that into g(x + 2). You need to find g(3 + 2) = g(5), which is (5 + 2)² = 49, our target number. Now, plug x = 3 into the answer choices, to see which one turns into 49. (E) is the correct answer.

You may also have to work with a split function—sometimes called a piecewise function. A split function is one that has different definitions, depending on some condition that is part of the function. Here are a couple of examples of split functions:

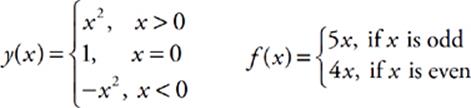
Functions of this type are fairly self-explanatory. It”s just necessary to check the conditions of the function before plugging values in to make sure you”re using the right function definition.

Drill

Practice working with functions in the following questions. The answers to these drills can be found in Chapter 12.

14. If f(x) = x² − x³, then f(−1) =

(A) −2

(B) −1

(D) 1

(E) 2

17. If f(z) = , then how much does f(z) increase as z goes from 7 to 8 ?

(A) 0.64

(B) 1.07

(D) 3.84

(E) 5.75

26. If g(t) = t³ + t² − 9t − 9, then g(3) =

(A) −9

(B) 0

(D) 27

(E) 81

29. If f(x, y) = , which of the following is equal to f(3, −6) ?

(A) −48

(B) −6

(D) 6

(E) 18

30. If h(x) = x² + x − 2, and h(n) = 10, then n could be which of the following?

(A) −4

(B) −3

(D) 1

(E) 2

33. The function f is given by f(x) = x • [x], where [x] is defined to be the greatest factor of x that does not equal x. What is f(75) ?

(A) 25

(B) 225

(D) 1,125

(E) 1,875

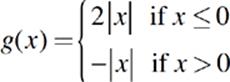
34. What is the value of g(−y) if y = 3 ?

(A) −6.0

(B) −3.0

(D) 1.5

(E) 6.0

COMPOUND FUNCTIONS

A compound function is a combination of two or more functions, in sequence. It”s essentially a function of a function—you take the output of the first function and put it into the second function. For example:

f(x) = x² + 10x + 3	g(x) =
g(f(x)) =

The expression g(f(x)) is a compound function made up of the functions f(x) and g(x). As with any algebraic expression with parentheses, you start with the innermost part. To find g(f(x)) for any x, calculate the value of f(x), and plug that value into g(x). The result is g(f(x)). Like questions based on simple algebraic functions, compound-function questions come in two flavors—questions that require you to plug numbers into compound functions and do the arithmetic, and questions that require you to plug terms with variables into compound functions and find an algebraic answer. For example:

f(x) = x² + 10x + 3

g(x) =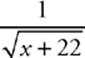

34. What is the value of g(f(−4)) ?

(A) 0.15

(B) 1.00

(D) 3.00

(E) 6.56

Here”s How to Crack It

To find the value of g(f(−4)), just plug −4 into f(x); you should find that f(−4) = −21. Then, plug −21 into g(x). You should find that g(−21) = 1. The correct answer is (B).

The more complicated type of compound-function question asks you to find the algebraic expression of a compound function. Essentially, that means you”ll be combining the definitions of two functions. Try an example.

f(x) = x² + 10x + 3

g(x) =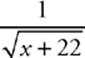

36. Which of the following is g(f(x)) ?

(A)

(B)

(C)

(D)

(E)

Here”s How to Crack It

Instead of doing lots of messy algebra, just pick an easy number to Plug In for x. Let”s try x = 3. So you”re looking for g(f(3)). Work from the inside out, f(3) = 42, so g(f(3)) = g(42). When you plug 42 into g, you get , the target number. Plugging x = 3 into the answer choices, you find that answer choice (B) hits that target.

Drill

Practice working with compound functions in the following questions. The answers to these drills can be found in Chapter 12.

17. If f(x) = 3x and g(x) = x + 4, what is the difference between f(g(x)) and g(f(x)) ?

(A) 0

(B) 2

(D) 8

(E) 12

24. If f(x) = |x| − 5 and g(x) = x³ − 5, what is f(g(−2)) ?

(A) −18

(B) −5

(D) 3

(E) 8

25. If f(x) = 5 + 3x and f(g(x)) = 17, then g(x) =

(A) 3

(B) 4

(D) 3 + 5x

(E) 5 + 3x

f(x) = x² + 10x + 25

g(x) = + 4

32. Which of the following is g(f(x)) ?

(A) x − 1

(B) x + 1

(D) x + 9

(E) x² − 2x − 1

f(x) =

g(x) = x³ − 2

36. What is the positive difference between f(g(3)) and g(f(3)) ?

(A) 0.7

(B) 0.9

(D) 3.4

(E) 6.8

INVERSE FUNCTIONS

Inverse functions are opposites—functions that undo each other. Here”s a simple example.

f(x) = 5x

f(x) =

Remember the
Machine?

Okay, so now we have
two machines. We drop
a number into one, and
it spits out a number. If
we drop that number into
the second machine, the
second machine spits out
our original number. The
two machines negate
each other.

Here, the function f(x) multiplies x by 5. Its inverse, symbolized by f⁻¹(x), divides x by 5. Any number put through one of these functions and then the other would come back to where it started. Here”s a slightly more complex pair of inverse functions:

f(x) = 5x + 2

f⁻¹(x) =

Here, the function f(x) multiplies x by 5 and then adds 2. The inverse function f⁻¹(x) does the opposite steps in reverse order, subtracting 2 and then dividing by 5. Let”s add one more step:

f(x) =

f⁻¹(x) =

f(g(x)) = x

Compound functions and inverse functions are often used together in questions on the Math Subject Tests. It”s characteristic of inverse functions that they have opposite effects—they undo each other. For that reason, whenever you see the statement f(g(x)) = x, you know that the functions f(x) and g(x) are inverse functions. When a value x is put through one function and then the other, it returns to its original value. That means that whatever changes f(x) makes are undone by g(x). The statement f(g(x)) = x means that g(x) = f ⁻¹(x).

Now, the function f(x) multiplies x by 5, adds 2, and then divides by 4. The inverse function f ⁻¹(x) once again does the reverse; it multiplies by 4, subtracts 2, and then divides by 5. An inverse function always works this way; it does the opposite of each operation in the original function, in reverse order.

The typical inverse-function question gives you the definition of a function and asks you to identify the function”s inverse.

40. If f(x) = + 3 and f(g(x)) = x, which of the following is g(x) ?

(A) x −

(B) x − 12

(D) 4x − 12

(E) 4(x + 12)

Here”s How to Crack It

In this question, the statement f(g(x)) = x tells you that f(x) and g(x) are inverse functions. Finding g(x), then, amounts to finding the inverse of f(x). You could do this by picking out the function that does the opposite of the operations in f(x), in reverse order; but there”s an easier way. By definition, inverse functions undo each other. In practice, this means that if you plug an easy number into f(x) and get a result, the inverse function will be the function that turns that result back into your original number.

For example, given the function f(x), you might decide to Plug In 8, a number that makes the math easy.

f(x) = + 3

f(8) = + 3

f(8) = 2 + 3

f(8) = 5

Invert x and y

If it doesn”t look like Plugging In will help you, another great way to find the inverse of a function is to switch x and y, or f(x). So if the original function is f(x) = 3x − 4, move it all around. First replace f(x) with y so you can see it all more easily. Now you have y = 3x − 4. Switch x andy: x = 3y − 4. Now solve for y; x + 4 = 3y; and 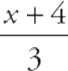= y. As a final touch, replace y with f⁻¹(x): f⁻¹(x) =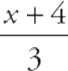. And you now have the inverse of f(x) = 3x − 4.

You find that f(x) turns 8 into 5. The inverse function g(x) will be the one that does the reverse—that is, turns 5 into 8. To find g(x), plug 5 into each of the answer choices. The answer choice that gives you 8 will be the correct answer. In this case, the correct answer is (D).

DRILL

Practice your inverse-function techniques on these questions. The answers to these drills can be found in Chapter 12.

22. If f(x) = and f(g(x)) = x, then g(x) =

(A) 2x +

(B)

(D) +

(E)

33. If f(x) = 4x² − 12x + 9 for x ≥ 0, what is f⁻¹(9) ?

(A) 1

(B) 3

(D) 12

(E) 16

35. If f(3) = 9, then f⁻¹(4) =

(A) −2

(B) 0

(D) 16

(E) It cannot be determined from the information given.

DOMAIN AND RANGE

Some function questions will ask you to make statements about the domain and range of functions. With a few simple rules, it”s easy to figure out what limits there are on the domain or range of a function.

Domain

The domain of a function is the set of values that may be put into a function without violating any laws of math. When you”re dealing with a function in the f(x) form, the domain includes all of the allowable values of x. Sometimes a function question will limit the function”s domain in some way, like the following:

For all integers n, f(n) = (n − 2)π. What is the value of f(7) ?

In this function, the independent variable n is limited; n can be only an integer. The domains of most functions, however, are not obviously limited. Generally, you can put whatever number you want into a function; the domain of many functions is all real numbers. Only certain functions have domains that are mathematically limited. To figure out the limits of a function”s domain, you need to use a few basic rules. Here are the laws that can limit a function”s domain.

Domain

An easy way to
think about it is that
the domain is all the
possible values of x.

Mathematical Impossibilities for Domain:

• A fraction having a denominator of zero: Any values that would make the bottom of a fraction equal to zero must be excluded from the domain of that function.

• The square root of a negative number: Any values that would make a number under a square root sign negative must be excluded from the domain of that function.

• Any even-numbered root of a negative number: This refers to, , etc. No value in the domain can make the function include an even-numbered root of a negative number.

Whenever a function contains a fraction, a square root, or another even-numbered root, it”s possible that the function will have a limited domain. Look for any values that would make denominators zero, or even-numbered roots negative. Those values must be eliminated from the domain. Take a look at these examples.

f(x) =

In this function, there is a variable in the denominator of a fraction. This denominator must not equal zero, so the domain of f(x) is {x ≠ 0}.

g(x) =

Once again, this function has a variable in the denominator of a fraction. In this case, the value of x that would make the denominator equal zero is −5. Therefore, the domain of g(x) is {x ≠ −5}.

t(a) = 4

This function has a variable under a square root sign. The quantity under a square root sign must not be negative, so the domain of t(a) is {a ≥ 0}.

s(a) = 3

Here again, you have a function with a variable under a square root. This time, the values that would make the expression negative are values greater than 10; all of these values must be eliminated from the function”s domain. The domain of s(a) is therefore {a ≤ 10}.

A function can involve both fractions and square roots. Always pay careful attention to any part of a function that could place some limitation on the function”s domain. It”s also possible to run into a function where it”s not easy to see what values violate the denominator rule or the square root rule. Generally, factoring is the easiest way to make these relationships clearer. For example:

f(x) =

Here, you”ve got variables in the denominator. You know this is something to watch out for, but it”s not obvious what values might make the denominator equal zero. To make it clearer, factor the denominator.

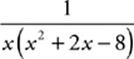
f(x) =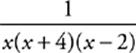

Now, things are much clearer. Whenever quantities are being multiplied, the entire product will equal zero if any one piece equals zero. Any value that makes the denominator equal zero must be eliminated from the function”s domain. In this case, the values 0, −4, and 2 all make the denominator zero. The domain of f(x) is {x ≠ −4, 0, 2}. Take a look at one more example.

g(x) =

Once again, you”ve got an obvious warning sign—variables under a radical. Any values of x that make the expression under the radical negative must be eliminated from the domain. But what values are those? Are there any? To make it clear, factor the expression.

g(x) =

The product of two expressions can be negative only when one of the expressions is negative and the other positive. If both expressions are positive, their product is positive. If both expressions are negative, their product is still positive. So the domain of g(x) must contain only values that make (x + 5) and (x − 1) both negative or both nonnegative. With a little experimentation, you”ll find that both expressions are negative when x < −5, and both expressions are nonnegative when x ≥ 1. The domain of g(x) is therefore {x ≤ −5} or {x ≥ 1}.

Domain Notation

The domain of a function is generally described using the variable x. A function f(x) whose domain includes only values greater than 0 and less than 24, could be described in the following ways:

The domain of f(x) is {0 < x < 24}.

The domain of f is the set {x: 0 < x < 24}.

A function in the form f(x) can be referred to either as f(x) or simply as f.

Range

The range of a function is the set of possible values that can be produced by the function. When you”re dealing with a function in the f(x) form, the range consists of all the allowable values of f(x). The range of a function, like the domain, is limited by a few laws of mathematics. Several of these laws are the same laws that limit the domain. Here are the major rules that limit a function”s range.

• An even exponent produces only nonnegative numbers. Any term raised to an even exponent must be positive or zero.

• The square root of a quantity represents only the positive root. Like even powers, a square root can”t be negative. The same is true for other even-numbered roots (, , etc.).

• Absolute values produce only nonnegative values.

Range

An easy way to think
about it is that the range
is all possible values of y.
In the case of functions,
the range is all the possible
values of f(x).

These three operations—even exponents, even roots, and absolute values—can produce only nonnegative values. Consider these three functions.

f(x) = x⁴

f(x) =

f(x) = |x|

These functions all have the same range, { f(x) ≥ 0}. These are the three major mathematical operations that often limit the ranges of functions. They can operate in unusual ways. The fact that a term in a function must be nonnegative can affect the entire function in different ways. Take a look at the following examples.

f(x) = −x⁴

f(x) = −

f(x) = −|x|

Each of these functions once again contains a nonnegative operation, but in each case the sign is now flipped by a negative sign. The range of each function is now {f(x) ≤ 0}. In addition to being flipped by negative signs, ranges can also be slid upward or downward by addition and subtraction. Take a look at these examples.

f(x) = x⁴ −5

f(x) = −5

f(x) = |x| − 5

Each of these functions contains a nonnegative operation that is then decreased by 5. The range of each function is consequently also decreased by 5, becoming {f(x) ≥ −5}. Notice the pattern: A nonnegative operation has a range of {f(x) ≥ 0}. When the sign of the nonnegative operation is flipped, the sign of the range also flips. When a quantity is added to the operation, the same quantity is added to the range. These changes can also be made in combination.

g(x) =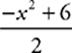

In this function, the sign of the nonnegative operation is flipped, 6 is added, and the whole thing is divided by 2. As a result, the range of g(x) is {g(x) ≤ 3}. The range of x², which is {y: y ≥ 0}, has its sign flipped, is increased by 6, and is then divided by 2.

Range Notation

Ranges can be represented in several ways. If the function f(x) can produce values between −10 and 10, then a description of its range could look like any of the following:

• The range of f(x) is given by {f: −10 < f(x) < 10}.

• The range of f(x) is {−10 < f(x) < 10}.

• The range of f(x) is the set {y: −10 < y < 10}.

Why Do I See y?

Because a function”s
range is represented on
they-axis when the function
is graphed, the range
is sometimes described
using the variable y, even
when y doesn”t appear in
the function.

Solving a Range Question

Now that you”ve learned about ranges, let”s try out a question. Take a look at the following example.

25. If f(x)|−x² −8| for all real numbers x, then which of the following sets is the range of f ?

(A) {y: y ≥ −8}

(B) {y: y > 0}

(D) {y: y ≤ 8}

(E) {y: y ≥ 8}

Here”s How to Crack It

Start out with what you know about the equation. Since the result of absolute value is a nonnegative number, you can eliminate (A) right away. Is there a maximum number that an absolute value creates? No. So you can also eliminate (D). Now look at x². We know that there”s no maximum that x² can be, but there is a minimum. The smallest x² can be is 0. If x² = 0, then the result inside the absolute value sign would be −8. This means that, when x = 0, f(x) = 8. So the answer is (E). Now you may be thinking, but what about that negative sign? Well, a negative minus a negative makes a number more negative and it”s in absolute value so it would get more positive. The smallest number that machine can produce is 8.

Plugging In on Range Questions

Because all questions on the Math Subject Tests are multiple choice, you can always Plug In and use POE on range questions. It may take a little longer but it gives you a chance to score another point. So, if you”re confused by the process of finding the range, or not sure what steps to take on a particular range question, Plug In!

Let”s take another look at question 25 on this page. If you Plugged In x = 3, you would find that f(3) = 17. From that info you could eliminate (D). If you Plugged In 0, you”d see that f(0) = 8. If you Plugged In numbers less than 0, you”d see that f(x) never gets smaller than 8. The answer is (E). You still get to the right answer!

FUNCTIONS WITHIN INTERVALS: DOMAIN MEETS RANGE

A question that introduces a function will sometimes ask about that function only within a certain interval. This interval is a set of values for the variable in the x position.

Remember?

Don”t forget that x
represents the
independent variable!

For example:

If f(x) = 4x − 5 for [0, 10], then which of the following sets represents the range of f ?

If f(x) = 4x − 5 for 0 ≤ x ≤ 10, what is the range of f ?

These two questions present the same information and ask the same question. The second version simply uses a different notation to describe the interval, or domain, in which f(x) is being looked at.

Be Careful

You have to be alert when
domains or ranges are
given in this notation, because
it”s easy to mistake
intervals in this form for
coordinate pairs. Tricky!

The example given above also demonstrates the most common form of a function-interval question, in which you”re given a domain for the function and asked for the range. Whenever the function has no exponents, finding the range is easy. Just plug the upper and lower extremes of the domain into the function. The results will be the upper and lower bounds of the range. In the example above, the function”s range is the set {y: −5 ≤ y ≤ 35}.

The interval that you are given means that, for that particular question, you have a different set of values for the function”s domain.

DRILL

Practice your domain and range techniques on the following questions. The answers to these drills can be found in Chapter 12.

24. If f(x) = , then which of the following sets is the domain of f ?

(A) {x: x ≠ −2, 0, 3}

(B) {x: x ≠ 0}

(D) {x: x > 0}

(E) {x: x > 3}

27. If g(x) = , then the domain of g is given by which of the following?

(A) {x: x ≥ −2}

(B) {x: x ≠ 3, 4}

(D) {x: −2 < x < 6}

(E) {x: x ≤ −2 or x ≥ 6}

30. If t(a) = , then which of the following sets is the range of t ?

(A) {y: y ≠ 0}

(B) {y: y ≥ 0}

(D) {y: y ≥ 1.67}

(E) {y: y ≥ 2.24}

34. If f(x) = 4x + 3 for −1 ≤ x ≤ 4, then which of the following gives the range of f ?

(A) {y: −4 ≤ y ≤ 7}

(B) {y: −4 ≤ y ≤ 19}

(D) {y: −1 ≤ y ≤ 19}

(E) {y: 1 ≤ y ≤ 19}

GRAPHING FUNCTIONS

All of the function techniques covered in this chapter so far have dealt with the algebra involved in doing functions. Most of the function questions on each Math Subject Test will be algebra questions like the ones you”ve seen so far. However, there”s another class of function questions that appears on the Math Subject Tests—graphical questions.

Graphical function questions require you to relate an algebraic function to the graph of that function in some way. Here are some of the tasks you might be required to do on a graphical function question:

• Match a function”s graph with the function”s domain or range.

• Match the graph of a function with the function”s algebraic definition.

• Decide whether statements about a function are true or false, based on its graph.

None of these tasks is very difficult, as long as you”re prepared for them. The next few pages will tell you everything you need to know.

Identifying Graphs of Functions

The most useful tool for identifying the graph of a function is the vertical-line test. Remember: A function is a relation of a domain and a range, in which each value in the domain matches up with only one value in the range. Simply put, there”s only one f(x), or y, for each x. Graphically, that means that any vertical line drawn through the x-axis can intersect a function only once. If you can intersect a graph more than once with a vertical line, it isn”t a function. Here”s the vertical-line test in action.

Looking at a Graph

When a function f(x) is graphed, the x-axis represents the values of x. The y-axis represents the values of f(x). When you look at the coordinates (x, y) of any point on the function”s graph, x represents a value in the function”s domain (the input of the function), and y represents the function of that value (the output of the function).

This is a function, because no vertical line can intersect it more than once. All straight lines are functions, with only one exception. A vertical line is not a function, because another vertical line would intersect it at an infinite number of points.

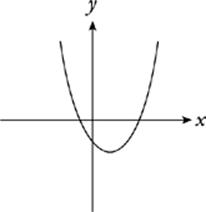
This is also a function. Any parabola that opens up or down is a function.

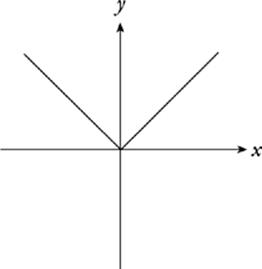
This is the graph of y = |x|, and it”s a function as well.

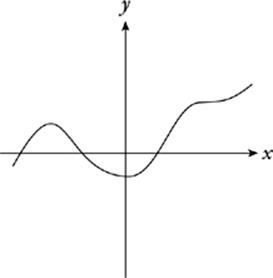
This complicated curve also passes the vertical-line test for functions.

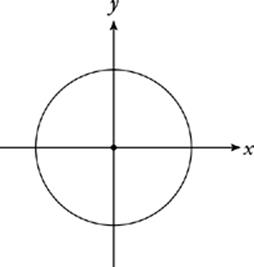
This is not a function; there are many places where a vertical line can intersect a circle twice.

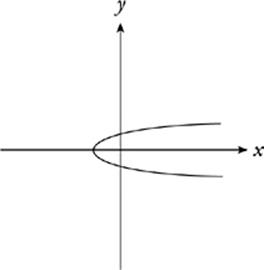
This isn”t a function either. Although this graph is parabolic in shape, it fails the vertical-line test.

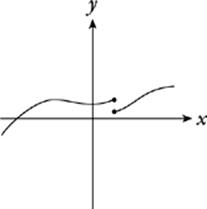
Nope. It”s close, but there”s one point where a vertical line can intersect this graph twice—it can”t be a function.

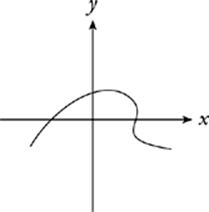
This curve is also not a function. It”s possible to cross this curve more than once with one vertical line.

DRILL

Use the vertical-line test to distinguish functions from nonfunctions in the following practice questions. The answers to these drills can be found in Chapter 12.

9. Which of the following could NOT be the graph of a function?

(A)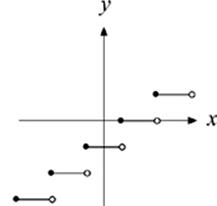

(B)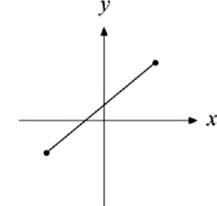

(C)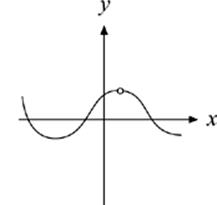

(D)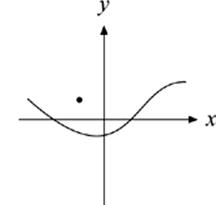

(E)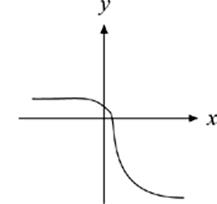

15. Which of the following could NOT be the graph of a function?

(A)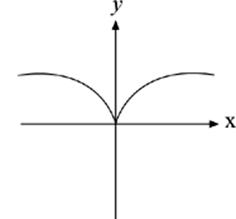

(B)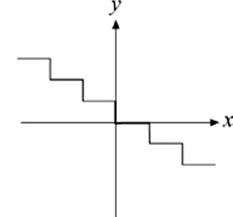

(C)

(D)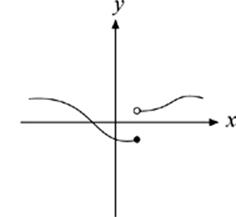

(E)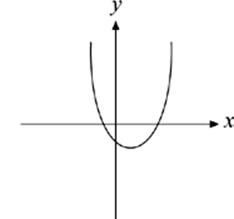

RANGE AND DOMAIN IN GRAPHS

The graph of a function gives important information about the function itself. You can generally state a function”s domain and range accurately just by looking at its graph. Even when the graph doesn”t give you enough information to state them exactly, it will often let you eliminate incorrect answers about the range and domain.

Take a look at the following graphs of functions and the information they provide:

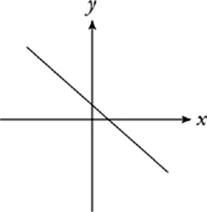
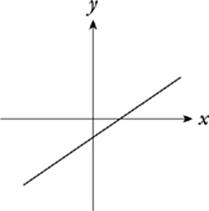
If you followed this line to the left, it would continue to rise forever. Likewise, if you followed it to the right, it would continue to fall. The range of this line (the set of y-values it occupies) goes on forever; the range is said to be “all real numbers.” Because the line also continues to the left and right forever, there are no x-values that the line does not pass through. The domain of this function, like its range, is the set of all real numbers.

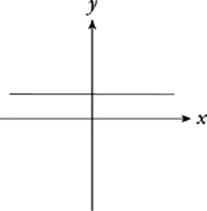
The same thing is true of all linear functions (whose graphs are straight lines); their ranges and domains include all real numbers. There”s only one exception. A horizontal line extends forever to the left and right (through all x-values) but has only one y-value. Its domain is therefore all real numbers, while its range contains only one value.

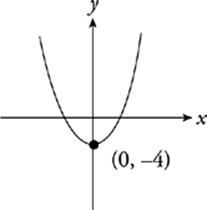
The domain of this function is the set of all real numbers, because parabolas continue widening forever. Its range, however, is limited. The parabola extends upward forever, but never descends lower along the y-axis than y = −4. The range of this function is therefore {y: y ≥ −4}.

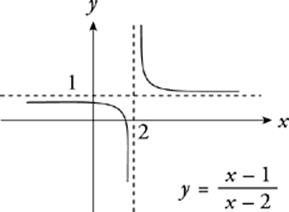
This function has two asymptotes. Asymptotes are lines that the function approaches but never reaches. They mark values in the domain or range at which the function does not exist or is undefined. The asymptotes on this graph mean that it”s impossible for x to equal 2, and it”s impossible for y to equal 1. The domain of f(x) is therefore {x: x ≠ 2}, and the range is {y: y ≠ 1}.

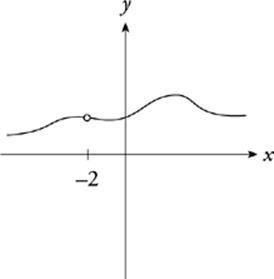
The hole in this function”s graph means that there”s an x-value missing at that point. The domain of any function whose graph sports a little hole like this one must exclude the corresponding x-value. The domain of this function, for example, would simply be {x: x ≠ −2}.

To estimate range and domain based on a function”s graph, just use common sense and remember these rules:

• If something about a function”s shape will prevent it from continuing forever up and down, then that function has a limited range.

• If the function has a horizontal asymptote at a certain y-value, then that value is excluded from the function”s range.

• If anything about a function”s shape will prevent it from continuing forever to the left and right, then that function has a limited domain.

• If a function has a vertical asymptote or hole at a certain x-value, then that value is excluded from the function”s domain.

• If you are asked to identify an asymptote, Plug In very large positive and negative numbers for x or y and see what values the other variable approaches. Try 1, 1,000, −1, −1,000, etc.

• Sometimes you can Plug In the answers (PITA) and see which values of x or y don”t make sense in the equation.

• Graphing the function on your calculator may be the easiest approach.

Drill

Test your understanding of range and domain with the following practice questions. The answers to these drills can be found in Chapter 12.

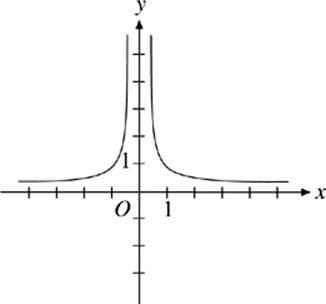
17. If the graph of y = f(x) is shown above, which of the following could be the domain of f ?

(A) {x : x ≠ 0}

(B) {x : x > 0}

(D) {x : x > 1}

(E) {x : x ≥ 1}

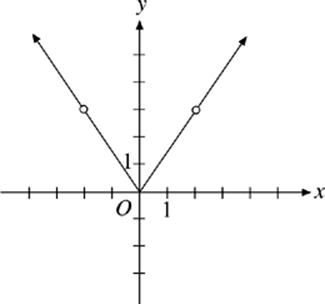
24. Which of the following could be the domain of the function graphed above?

(A) {x : x ≠ 2}

(B) {x : −2 < x <2}

(D) {x : |x| ≠ 2}

(E) {x : |x| > 2}

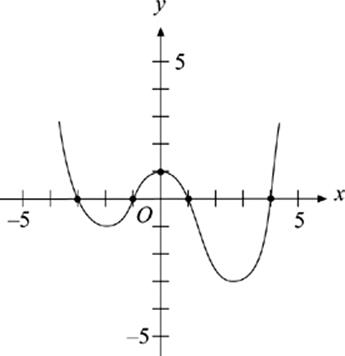
28. If y = g(x) is graphed above, which of the following sets could be the range of g(x) ?

(A) {y : y ≤ −1}

(B) {y : y ≥ −1}

(D) {y : −3 ≤ y ≤ −1}

(E) {y : y ≤ −3 or y ≥ −1}

37. Which of the following lines is an asymptote of the graph of y = 3e^−2x + 5 ?

(A) x = 0

(B) x = −2

(D) y = 0

(E) y = −6

48. Which of the following lines is an asymptote of the graph of y = ?

I. x = 2

II. y = −

III. y = −1

(A) I only

(B) II only

(D) I and II only

(E) I and III only

ROOTS OF FUNCTIONS IN GRAPHS

The roots of a function are the values that make the function equal to zero. Hence, the roots are also called zeros or solutions of the function. To find the roots of a function f(x) algebraically, you simply set f(x) equal to zero and solve for x. The values of x that you find are the roots of the function.

Graphically, the roots of a function are the values of x at which the graph crosses the x-axis, that is, the x-intercepts. That makes them easy to spot on a graph. If you are asked to match a function to its graph, it”s often helpful to find the roots of the function using algebra; then it”s a simple matter to compare the function”s roots to the x-intercepts on the graph. Take a look at this function:

f(x) = x³ + 3x² − 4x

If you factor it to find its roots, you get:

f(x) = x(x + 4)(x − 1)

The roots of f(x) are therefore x = −4, 0, and 1. You can expect the graph of y = f(x) to cross the x-axis at those three x-values.

DRILL

Try the following practice questions by working with the roots of functions. The answers to these drills can be found in Chapter 12.

16. Which of the following is a zero of f(x) = 2x² − 7x + 5 ?

(A) 1.09

(B) 1.33

(D) 2.50

(E) 2.75

19. The function g(x) = x³ + x² − 6x has how many distinct roots?

(A) 1

(B) 2

(D) 4

(E) It cannot be determined from the information given.

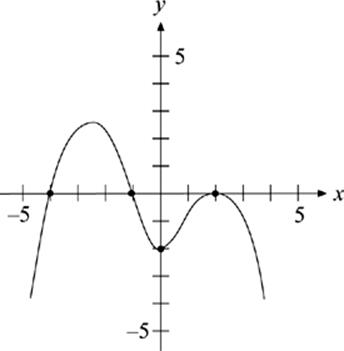
25. If the graph of y = f(x) is shown above, which of the following sets represents all the roots of f(x) ?

(A) {x = −2, 0, 2}

(B) {x = −4, −1, 0}

(D) {x = −4, −1, 2}

(E) {x = −4, −1}

SYMMETRY IN FUNCTIONS

Symmetry Across the y-Axis (Even Functions)

When a function contains exponents and fractions and you”re given an interval, you”ll have to take the question in two steps. First, Plug In the upper and lower limits of the domain of the function. Then use the range techniques from the previous section to see whether there are other limits on the function”s range. If the paper were folded along the y-axis, the left and right halves of the graph would meet perfectly. Functions with symmetry across the y-axis are sometimes called even functions. This is because functions with only even exponents have this kind of symmetry, even though they are not the only even functions. Look at the graph of y = cos x on the next page.

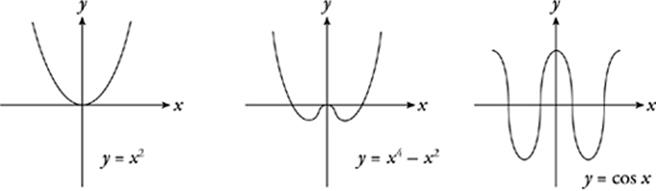
Even Functions

This is the algebraic definition of symmetry across the y-axis:

A function is symmetrical across the y-axis when

f(−x) = f(x)

This means that the negative and positive versions of any x-value produce the same y-value.

Origin Symmetry (Odd Functions)

A function has origin symmetry when one half of the graph is identical to the other half and reflected across the point (0, 0). Functions with origin symmetry are sometimes called odd functions, because functions with only odd exponents (as well as some other functions) have this kind of symmetry.

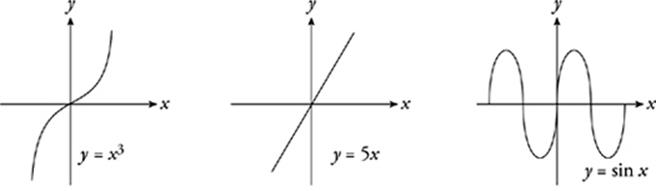
Odd Functions

This is the algebraic definition of origin symmetry:

A function has origin symmetry when

f(−x) = −f(x)

This means that the negative and positive versions of any x-value produce opposite y-values.

Symmetry Across the x-Axis

Some equations will produce graphs that are symmetrical across the x-axis. These equations can”t be functions, however, because each x-value would then have to have two corresponding y-values. A graph that is symmetrical across the x-axis automatically fails the vertical-line test.

Questions asking about symmetry generally test basic comprehension of these definitions. It”s also important to understand the connection between these algebraic definitions and the appearance of graphs with different kinds of symmetry.

DRILL

Try these practice questions. The answers to these drills can be found in Chapter 12.

6. Which of the following graphs is symmetrical with respect to the x-axis?

(A)

(B)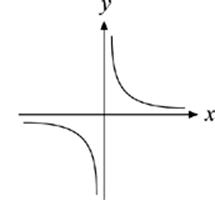

(C)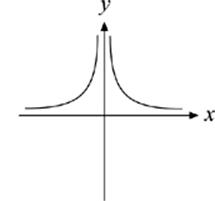

(D)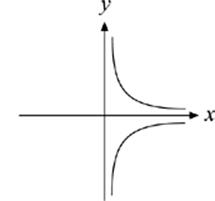

(E)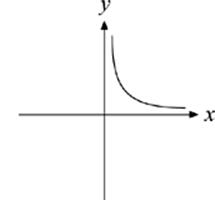

17. If an even function is one for which f(x) and f(−x) are equal, then which of the following is an even function?

(A) g(x) = 5x + 2

(B) g(x) = x

(D) g(x) = x³

(E) g(x) = −|x|

Periodic Functions

A periodic function is a function that repeats a pattern of range values forever. Always look for a pattern when you”re dealing with a periodic function.

Remember?

We also talked about
periodic functions in the
Trigonometry section.

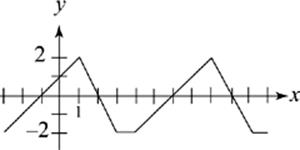
40. Two cycles of periodic function f are shown in the graph of y = f(x) above. What is the value of f(89) ?

(A) −2

(B) −1

(D) 1

(E) 2

Here”s How to Crack It

In this question, we need to find the period of the function, that is, how often it repeats its range values. Find the pattern. From peak to peak, it goes from x = 1 to x = 8. This means that the function repeats itself every 7 units (the period is 7). Where does 89 fall in this pattern? Well, you want to take away multiples of 7 from 89, to find out an equivalent range value on the graph above. So, f(89) = f(82) = f(75)…and so on. Since 89 ÷ 7 = 12 remainder 5, this means that f(89) = f(5). From the graph, f(5) = −1, and the answer is (B).

Movement of a Function

When giving you a function question, ETS may decide to fool around with the variable. Sometimes you”ll be asked how this affects the graph of the function. For example, ETS may show you f(x) and ask you about the graph of |f(x)|. You can either Plug In points or know the following rules.

In relation to f(x):

• f(x) + c is shifted upward c units in the plane

• f(x) − c is shifted downward c units in the plane

• f(x + c) is shifted to the left c units in the plane

• f(x − c) is shifted to the right c units in the plane

• −f(x) is flipped upside down over the x-axis

• f(−x) is flipped left-right over the y-axis

• |f(x)| is the result of flipping upward all of the parts of the graph that appear below the x-axis

Of course, you may have to combine these rules. If so, Plugging In some points may be the easiest way to go.

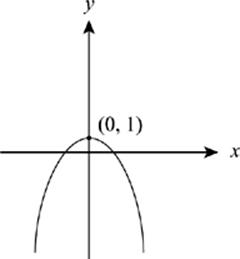
45. The graph of y = f(x) is shown above. Which of the following is the graph of y = −f(x + 1) ?

Mirror, Mirror on
the Axis

A function that seems
to have a mirror image
reflected in the y-axis is
symmetrical across the
y-axis.

(A)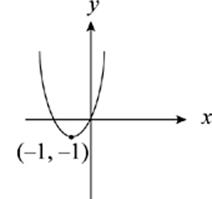

(B)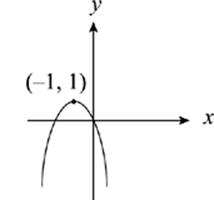

(C)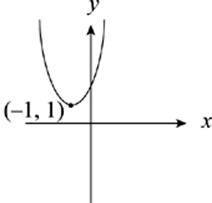

(D)

(E)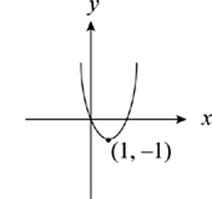

Here”s How to Crack It

To figure out what happens to the graph of f(x), just use the rules on this page. The x + 1 inside the parentheses shifts the graph one unit to the left. If this were the final answer, the vertex would be at (−1, 1). Now you have to take care of the negative sign outside the function. It reflects the entire function across the x-axis, so the vertex gets reflected to (−1, −1) and the parabola opens upward. If you reflected first and then shifted to the left, you”d get the same result. The answer is (A).

DEGREES OF FUNCTIONS

The degree of a polynomial is the highest degree of any term in the polynomial. The degree also determines at most how many distinct roots the polynomial will have. For example, the function p(x) = x³ − 4x² + 7x − 12 is a third-degree function. This means that p(x) has at most three distinct roots. These roots can be distinct or identical. A sixth-degree function can have at most 6 distinct roots. It can actually have anywhere from 0 to 6 distinct roots. Let”s take a look at two sixth-degree functions:

f(x) = x⁶

g(x) = (x − 1)(x − 2)(x − 3)(x − 4)(x − 5)(x − 6)

Getting the Third (or
Fourth or Fifth…)
Degree

The degree of a term in
a polynomial is the sum
of the exponents of the
variables in that term. So
if the term in a polynomial is
3xy², the degree of that
term is 3.

The function f(x) has six roots, but they”re all the same: f(x) = 0 when x = 0, which makes the function equal 0• 0• 0• 0• 0• 0. Basically, the function has six roots of zero—it has only one distinct root. The function g(x) has six distinct roots: g(x) = 0 when x = 1, 2, 3, 4, 5, or 6. Another example is that a function might have four roots of 2, a root of 3, and a root of 4, for a total of three distinct roots. The equation of this function would look like

f(x) = (x − 2)⁴(x − 3)(x − 4)

Math Vocab

Remember that distinct
means different.

This is still a sixth-degree function, and it has six roots. That”s the algebraic meaning of the degree of a function: It equals the maximum number of roots that the function has.

The degree of a function tells you a great deal about the shape of the function”s graph. Take a look at the graphs on the following pages.

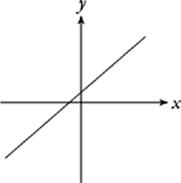
This is the graph of a first-degree function. All first-degree functions are linear functions, whose graphs are straight lines. A first-degree function has no extreme values—that is, it has no point which is higher or lower than all of the others.

An Important
Distinction

There is an important
distinction to make. The
shape of the graph of
f(x) = x⁶ will be very different
from the shape of the
graph of g(x) = x³. Even
though the root of each
is 0, it”s the degree that
determines the shape. So
these graphs would be
quite different. Take a look
at them on your graphing
calculator.

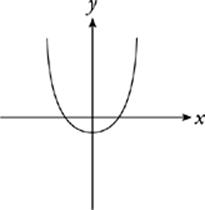
A second-degree function is usually a parabola. The function graphed above must be at least a second-degree function. A second-degree function has one extreme value, a maximum or minimum. This function”s extreme value is a minimum.

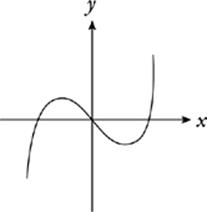
A third-degree function can have as many as two local extreme values. The function graphed above, which has a local maximum and a local minimum, must be at least a third-degree function. A “local” maximum (or minimum) means the values of the function are bigger (or smaller) than all of the surrounding values, but that the function may be bigger (or smaller) at some distant values of x.

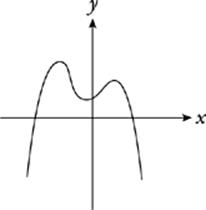
A fourth-degree function can have as many as three local extreme values. The function above has three extreme values, two local maxima and a local minimum between them. It must be at least a fourth-degree function.

By now, you should see the pattern. A fourth-degree function can have a maximum of three extreme values in its graph; a fifth-degree function can have a maximum of four extreme values in its graph. This pattern goes on forever. An nth-degree function has a maximum of n distinct roots and a maximum of (n − 1) extreme values in its graph. These two rules are the basis of a number of Math Level 2 questions. Take a look at the following practice questions.

DRILL

The answers to these drills can be found in Chapter 12.

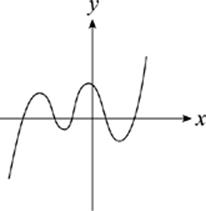
31. If the graph above is a portion of the graph of y = f(x), then which of the following could be f(x) ?

(A) ax + b

(B) ax² + bx + c

(D) ax⁴ + bx³ + cx² + dx + e

(E) ax⁵ + bx⁴ + cx³ + dx² + ex + f

35. If g(x) is a fourth-degree function, then which of the following could be the definition of g(x) ?

(A) g(x) = (x − 3)(x + 5)

(B) g(x) = x(x + 1)²

(D) g(x) = x(x + 8)(x − 1)²

(E) g(x) = (x − 2)³(x + 4)(x − 3)

Reviewing Functions Further

It”s impossible to cover every aspect of functions that may turn up on the Math Subject Tests; this is one of the most varied question categories on the tests. To be thoroughly prepared for function questions on the Math Subject Tests—particularly on the Math Level 2—you should read this chapter carefully and then take a cruise through your precalculus textbook.

Summary

· Algebraic functions are the functions with weird symbols. They tell you what to do. Just follow the directions of the function.

· Mathematical functions relate two sets of numbers: the domain and the range. Think of it like a machine. You put in one number, and the machine spits out another number.

· A compound function is a combination of two or more functions. It”s like having two machines. You put your number in one machine, and you take the result from that and put it into the second machine.

· Inverse functions are opposites. Here are a couple of specifics:

· An example of what inverse functions do is the following: If you put 5 into your first machine and get 12, then you put 12 into the inverse of that machine, you”ll get 5.

· Inverse functions will be symbolized either by f ⁻¹(x), or f(g(x)) = x.

· Inverse function questions can be solved, either by Plugging In or by replacing f(x) with y, switching x and y in the equation and solving.

· Domain is all the possible values of x in a given function. These are the numbers you put into the function. They are independent.

· Range is all the possible values of y (or f(x)) in a given function. These are the numbers you get out of the function. They are dependent.

· In order to figure out if a graph is a function, use the vertical line test. The line will touch only one point on the graph if the graph is a function.

· When answering domain and range questions with graphs, take a look to see what values x can”t be and what values y can”t be.

· The roots of a function will make the function equal to 0 when you substitute them for the independent variable. Graphically, a function crosses the x-axis at its root values.

· There are a few types of symmetry discussed in this chapter. An easy way to think about symmetry is this: If you physically folded your paper along the line of symmetry and all the points on both sides touched, the graph would be symmetrical along that line.

· A function is symmetrical across the y-axis when f(−x) = f(x). This is called an even function.

· A function has origin symmetry when f(−x) = −f(x). This is called an odd function.

· A graph that is symmetrical across the x-axis isn”t a function, because it fails the vertical line test.

· You may see questions that ask about the movement of a function. If the number is outside the parentheses of the function, the graph shifts along the y-axis. If it is inside the parentheses, the graph shifts along the x-axis.

· The following is only for people taking the Level 2 Subject Test:

· A periodic function is a function that repeats a pattern of range values forever.

· The degree of a term is the sum of the exponents in that term.