University Mathematics Handbook (2015)
VIII. Integral Calculus of Multivariable Functions
Chapter 6. Triple Integrals
6.1 Definition
Let function 
be defined above solid 
in three-dimensional space of volume 
. Let us divide into elementary solids 
, of volumes 
, respectively. Let's choose, in every 
, point 
and construct integral sum
If there exists 
, when the maximum diameter of solids tends to zero and the limit is independent of the partition of and the choice of points 
, then it is called triple integral of 
over and is denoted as either
or 
or 
6.2 Properties of Triple Integrals
The properties of triple integrals are similar to those of double integrals (see chap.2.2). Let us just mention the following:
a. Volume of solid is 
.
b. If function is integrable over , and holds 
for every 
, then
c. If function is integrable over , then 
is integrable in the same domain, and
6.3 Triple Integrals Calculation
a. If function is integrable over rectangular parallelepiped 
,
then 
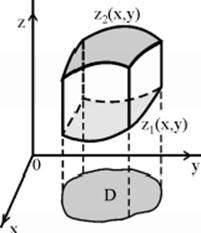
b. If function is integrable above cylindrical body bounded between two surfaces 
, 
above region 
on plane 
(Figure 1), then
|
|
|
|
Figure 1 |
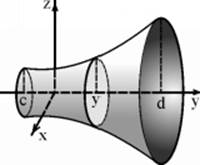
Figure 2 |
c. If body 
is between planes 
and 
, and for every constant 
of 
the plane parallel to these planes carves area 
from body 
(Figure 2), then
.
6.4 Change of Variables in Triple Integrals
a. If the system of functions 
, 
, 
, and 
, continuous and with continuous partial derivatives, maps 
to body with one-to-one correspondence and the Jacobian
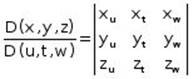
is different from zero, then
b. In cylindrical coordinates 
, 
, 
, the Jacobian is
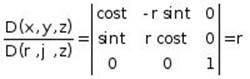
c. In spherical coordinates: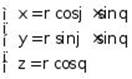 
,
the Jacobian is
6.5 Applications of Triple Integrals
a. Volume of the body: .
b. Mass of a body consisting of a material with specific gravity 
is 
.
c. Static moments of inertia 
, 
, 
in relation to planes 
, 
, and 
, respectively, is
, 
,
d. Center of mass 
of body :
when 
are static moment calculated using the formulas mentioned in paragraph c, and m is the mass of the body calculated by formula mentioned in paragraph b.