University Mathematics Handbook (2015)
X. Algebra
Chapter 1. Complex Numbers
1.1 Definition: Algebraic Operations in Complex Numbers
a. An ordered pair of real numbers 
is called a complex number.
b. 
, when 
, is the algebraic form of a complex number.
is called the real part of 
, and is denoted 
.
is called the imaginary part of , and is denoted 
.
c. 
is a conjugate to the number
d. Let 
and 
be two complex numbers:
1. Equality: 
if and only if 
and 
2. Addition: 
3. Multiplication: 
4. Powers of 
: , 
, 
5. Division: 
6. 
1.2 Geometric Description, Modulus and Argument
a. Any complex number 
can be described as point in plane 
or a vector beginning in the origin and ending at point 
.
Plane 
is called complex plane, when -axis is Real Axis and -axis is Imaginary Axis.
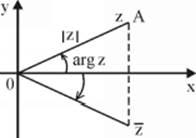
b. In the complex plane, 
is described by a vector symmetrical to about -axis.
c. The length of vector 
s called the modulus or absolute value of complex number 
and is denoted 
.
d. Angle 
between the vector corresponding to complex number and the positive direction of the real axis is called the argument of and is denoted as 
. It is measured counterclockwise, in radians.
Notice: For every complex number, the modulus is specified definitely, but an argument has countless values different from each other by an integer product of 
.
e. 
is the polar form of a complex number. To have its polar form, we should just take an argument value of 
, or, alternately, 
, since an addition of 
for does not change the values of 
and 
.
f. The relation between the algebraic form 
and the polar form 
of a complex number is:
g. Properties of absolute value (modulus)
h. Properties of the argument
1.3 Powers and Roots of
a. De Moivre’s Formula: For every natural 
,
b. The -th root of a complex number is a complex number 
holding 
. It is denoted 
.
c. For every complex number 
, 
there exist just different complex numbers 
for which 
, expressed by the formula
