One-Dimensional Wave Equation - Partial Differential Equations (PDE)

University Mathematics Handbook (2015)

XIV. Partial Differential Equations (PDE)

Chapter 5. One-Dimensional Wave Equation

(*)

when is the velocity of wave propagation.

If , then it is a homogeneous equations.

5.1 General Solution of Homogeneous Equation

a. , are characteristic lines.

b. By change of variables , we get the canonical form of a wave equation . Its solution is , when functions are arbitrary, continuous, and have partial derivatives continuous up to second order.

c. is a general solution of (*).

d. describes a (rightwards) forward wave at speed .

describes a (leftwards) backward wave at speed .

General solution is a superposition of an forward wave and a backward wave with speed .

5.2 Vibrations of an Infinite String. D'Alembert's
Formula

a. Equations system

(*)

(**)

describes the amplitude of an (ideal) elastic infinite string vibration. Initial conditions and are given functions describing amplitude and vibration velocity at time .

b. (*),(**) is called a Cauchy problem.

c. If and , then Cauchy problem (*),(**) has unique solution given by D'Alembert's formula

(***)

d. If is continuous, , are piecewise continuous, and and/or , then there are points where the first and second order derivatives of do not necessarily exist, and therefore, function given by (**) is not a solution of problem/ (*), (**).
In any point except these ones, is a solution of the wave problem. In this case, we construct a generalized solution of the wave problem, the following way:

Choose two sequences , , when , , uniformly converging to and , respectively, in .

Let the sequence be a solution of (*) holding.

Then, the sequence uniformly converges to the generalized solution, .

5.3 Non-Homogeneous Wave Equation

a. The equations system

(*)

(**)

describes a vibration of an infinite string constrained by an external force . String amplitude is dependent of initial conditions and initial velocity at time .

b. The characteristic triangle

Through point , we draw 2 characteristic lines:

forming, together with the -axis, a characteristic triangle (see illustration).

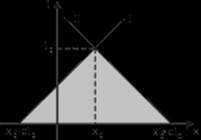
c. If, in (**), and , then, the solution of (*) is

d. If , and functions and are continuous on , , then the unique solution of Cauchy problem (*),(**) is

5.4 Vibrations of Semi-Infinite String

a. Homogeneous cauchy problem:

(*)

Initial condition:

(**)

Boundary condition:

(***)

The solution is

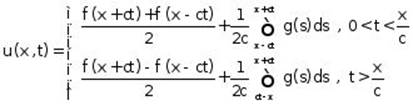
b. The solutions of non-homogeneous problem

with the same initial condition (**) or boundary condition (***) are

when is the solution of homogeneous problem (see a.) and

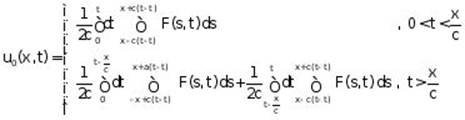
c. If, in a Cauchy problem, the boundary condition is non-homogeneous, that is, (***) is replaced by , then, by substituting , we get the non-homogeneous problem

5.5 Vibrationof a Finite String (Both Ends Fixed)

The finite string wave equation is

Initial condition is:

Boundary condition is:

To use D'Alembert’s formula (see 5.3), we extend functions , , on all -axis, through interval ends and , to odd and periodic functions with a period, that is