5 Steps to a 5 500 AP Physics Questions to Know by Test Day (2012)
ANSWERS
Chapter 1: Vectors
1. (C) (13.î - 6.ĵ) in which all the î components are added together to get the resultant vector î component and similarly with the ĵ component.
2. (C) They state a direction but not a magnitude.
3. (D) It states a magnitude but not a direction. Although it is one dimensional and has a direction of change, temperature is only a magnitude and, therefore, a scalar.
4. (D) Speed states only a magnitude, and velocity states a magnitude and direction. Although (B) is a true statement, it is not an explanation of the difference between the two terms.
5. (C) This is because magnitude is expressed by R, and direction is expressed by θ and.
6. (A) 1,520 is the correct answer when considering significant figures. Vector magnitude is the square root of the sum of the squared components.
7. (A) 9° is the correct answer when considering significant figures. The angle is given by taking the arctangent of the y component divided by the x component.
8. (C) |A| · |B| · cos θ.
9. (C) |A| · |B| · sin θ directed perpendicular to the plane of A and B. Because A is first in the equation, using the right-hand rule and sweeping A into B gives the direction from the plane containing A and B.
10. (D) Moles.
11. (D) 42 and 27 account for significant figures. x component = magnitude × cos (33°) and y component = magnituda × sin (33°).
12. (D) 42.î + 27.ĵ - 29.k. Using the magnitude, first calculate the z component and the component in the x-y plane. Then using the x-y plane and the x component, calculate the x and y components.
13. (B) 41.î + 10.ĵ + 98.k is obtained by adding the individual x, y, and z components.
14. (C) 0.1 mi î + 1.1 mi ĵ. While the hiker is 1.1 miles from his starting point, a vector quantity was requested.
15. (C) Force. All the others listed are scalar quantities.
16. (D) (A), (B), and (C) are just three of the many uses of vectors.
17. (E) 38.4°. First, the magnitude of the x - yplane component must be calculated; it is 67.6. Then, take the arctangent of the x component divided by the x y plane magnitude. The result is arcos (53/67.6) = 38.4°.
18. (B) 66.8°. Similar to Question 17, the magnitude of the vector must be calculated, which is 73.6. Then, take the arcos (29/73.6) = 66.8°.
19. (B) A vector.
20. (D) A scalar or a vector depending on whether the multiplication is the dot product or the cross product.
21. (B) −546.0. In this case, the dot product is the product of the two magnitudes.
22. (C) 0.0. In this case, the two vectors have a combined angle of 180°. Then, the magnitude of the cross product vector is |A| · |B| · sin θ = 0, with θ = 0°.
23. (D) It defines the positive or negative direction of the cross product vector.
24. (C) 0.0. The dot product is |A| · |B| · cos θ = 0, with θ = 90°.
25. (B) 546.0 k. The cross product vector is |A| · |B| · sin θ = 546, with θ = 90°, and a direction in the positive z direction.
26. (D) No, because the only information provided is a direction without a magnitude.
27. (B) A + B = B + A.
28. (D) The cross product gives a vector perpendicular to A and a cos 90° = 0.
29. A = 13 N î + 11 N ĵ + 17 N k and B = - 7.5 N î + 13 N ĵ + 15 N k. A · B = 300. N2. A × B −56 N î - 322 N î + 252 N k.
30. Using Earth and Alkaid as a reference direction, Merak is 25.6° from Alkaid. So, with that information we know two vector magnitudes and the angle between those vectors. Adding the two vectors gives us the distance from Alkaid to Merak. Then, 138 ly cos (25.6°) gives us the vector component along the reference line from Earth to Alkaid, and 138 ly sin (25.6°) gives us the vector component perpendicular to the reference line. Then, find the magnitude by adding the vector components and taking the square root of the squares of the components. This result is 210 light years between Alkaid and Merak.
Chapter 2: Free-Body Diagrams and Equilibrium
31. (A) The first, which mathematically states that Σ F = 0.
32. (D) According to Newton’s third law, it is the weight of the book and the pushback force of the table.
33. (C) When the object is on an inclined plane. The normal force is then a function of the slope of the inclined plane and will be less than the object’s weight. In the other cases, the object either has an equal or nonexistent normal force.
34. (C) A free-body diagram (FBD) of the string shows that an angle must exist between the string and a perfectly straight line to allow vertical forces to balance the weight of the string.
35. (E) Σ Fx = 0, Σ Fy = 0, Σ Fz = 0, Σ Mx = 0, Σ My = 0, and Σ Mz = 0 is the complete expression of Newton’s first law for the x, y, z coordinate system.
36. (C) A force applied to a body that causes the body to rotate. Some of the other answers do not completely explain the definition of torque.
37. (E) Generally, no. A rope can carry a compressive force if that force is applied perpendicular to the rope, but that is an extremely rare case.
38. (C) It is a force that is proportional to the normal force that acts in opposition to the direction of motion.
39. (C) An FBD shows the forces and accelerations and their locations acting on a body.
40. (D) The distance perpendicular to the line of action of the force from the pivot point.
41. (B) 200 pounds. The pulley simply redirects the force applied to the rope by the box.
42. (B) The answer is 498 N when using the proper significant figures. The calculated answer is 497.5, but it needs to be rounded to 498 to be correct.
43. (D) Tright = 1,610 N and Tleft = 2,630 N. There are two unknowns (i.e., the tensions in each rope), but there are two equations that define the x and y components of the tensions. Solving both equations will yield the above results when using significant figures.
44. (D) 1,000 N. Using the summation of moments about the tip yields the force applied 2 cm from the tip.
45. (C) 26° is found from the arctan, (0.5) = 26°.
46. (E) The astronaut moves in the direction of the force on the wrench. With no gravity to restrain him, the astronaut will move in response to the forces applied to him or those generated by him. In this case, the bolt cannot be loosened unless the astronaut is somehow fixed so he can apply force to the wrench. Otherwise, the force he applies will cause him to move in the direction of the force. The massive satellite is unlikely to rotate because of its high moment of inertia.
47. (B) 100 N is found by the summation of moments about the rear wheels. Account for significant figures.
48. (C) 1,633 N. A six-strand pulley has six supporting cables. Thus, the tension in the cable, which is continuous through the pulleys, is simply the total load divided by 6.
49. (B) Philosophiæ Naturalis Principia Mathematica, which was originally published in 1687.
50. (D) The weight of the object in the downward direction and the supporting force of the spring in the upward direction.
51. (E) The weight of the box, the resultant force of the plane on the box, and the friction force along the surface of the plane beneath the box. These are the only forces acting on the box. The others mentioned are components or they are misleading.
52. (A) 213 N is found by the summation of moments about the lift point.
53. (C) 1,760 N and 1,960 N. In (A) and (B), the buoyancy force caused by displacing the water acts opposite to the weight of the chest, so the force to pull up the chest is 1,760 N. Once out of the water, the full weight of the chest must be supported, so a force of 1,960 N is needed.
54. (C) 333 N is found by the summation of moments about the fulcrum. Since a vertical force is called for, accounting for the angle is unnecessary.
55. (D) 4.73 × 106 m from the Earth. This problem is similar to the question about the summation of moments, except that the masses are used instead of the weights.
56. (B) 682 N. The pulley effectively divides the weight of the block along the plane by 2.
57. (D) At the front center of the machine. That way, all three men are pushing the machine straight into the niche.
58. (B) 50 N. This problem depends on the given distances, which form a triangle with an angle of 0.5723° between the vertical rope position and the position where the bridge section is to be moved. The required force is the sin of that angle, then multiplied by the weight of the bridge section.
59. 1,048 N is the tension in the rope. This includes the weight along the plane, the friction force from the normal weight to the plane, and the pulley dividing the force by 2. This problem is similar to Question 26, but this question includes friction.
60. This is a simple summation of moments problem, but it is slightly obscured by the pulley and the use of significant figures. The answer is less than 26,000 N.
Chapter 3: Kinematics
61. (B) You know the height (120 m) and the initial velocity (0 m/s). The acceleration due to gravity (9.8 m/s2) is implied. Solve this equation for t:
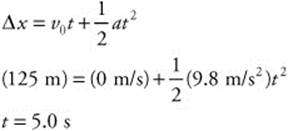
62. (D) You know the distance the car traveled (500 m), the initial velocity (0 m/s), and the final velocity (50 m/s). Solve this equation for a:
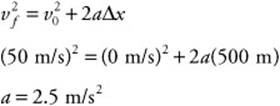
63. (C) The horizontal velocity of the package is the same as that of the plane (50.0 m/s). The height of the plane is 125.0 m. You must first find the time it takes for the package to reach the ground and use that time to calculate the horizontal distance that the package travels.
1. Solve for time:
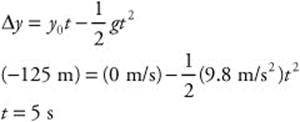
2. Solve for horizontal distance:
Δx=vxt
Δx=(50.0 m/s)(5s)
Δx=250m
64 (D) You know the angle of the kick (30°) and the initial velocity (10.0 m/s). You must find the vertical component of the velocity and solve for t when the ball hits the ground (y = 0).
1. Solve for vertical component of velocity:
vy = v sin θ
vy = (10.0 m/s)(sin 30°)
vy = 5.0 m/s
2. Solve for time:
65. (C) The object is at rest during the time interval of 3-4 s when the object’s position does not change.
66. (D) You know the car’s final velocity (30 m/s), the rate of acceleration (3.0 m/s2), and the time interval over which it accelerated (5.0 s). You can calculate the initial velocity:
vf = v0 + at
v0 = v0 - at
v0 = (30 m/s2)(5 s)
v0 = 15 m/s
67. (C) The airplane’s initial velocity was 0 m/s and it accelerated at 1.0 m/s2 for 5 min (300 s). You can calculate the distance:
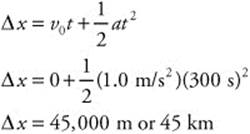
68. (B) By subtracting the echo time, you can calculate that the stone takes 8 s to reach the bottom of the well. Now, you can calculate the vertical distance of the well:
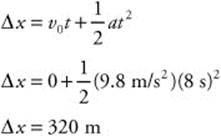
69. (E) At the maximum height, the velocity (vf) is zero. So, solve the equation vf = v0 + at for t.
70. (B) To get the velocity, take the derivative of x(t) = 4t2 + 6t + 2 and you will get v (t) = 8t + 6. At t = 6 s, v = 8(t) + 6 = 38 m/s. To find the original direction of motion, evaluate the expression for t = 0 s. You get v = 8(0) + 6 = 6 m/s.
71. (E) The initial velocity is 0 m/s, the height is 15 m, and the time is 1 s. You can calculate the acceleration due to gravity:
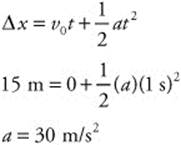
72. (A) You know the car’s initial velocity (0 m/s), the rate of acceleration (3.0 m/s2), and the distance of the track (150 m). You can calculate the final velocity:
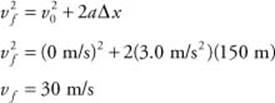
73. (D) The first derivative of a position-time function is a velocity-time function. The velocity at any instant in time is the slope of the line tangent to any point on the position-time graph. When the tangent line is horizontal (slope = 0), then the velocity is zero at that point. For this graph, that occurs at 1 s and 3 s.
74. (C) A projectile launched at an angle from the ground follows a parabolic path. The parabola is symmetrical, so the maximum height occurs at one-half of the total time in the air.
75. (D) It takes approximately 3 s for the stone to drop and the stone started from rest. So, we can calculate the approximate height of the cliff:
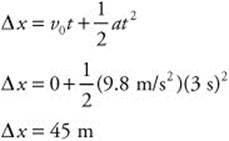
76. (D) The bicycle’s initial velocity was 5.0 m/s, and it slowed at an acceleration of −2.5 m/s2 to a stop (vf = 0). The time can be determined from this equation:
vf = v0 + at
(0 m/s) = (5.0 m/s) + (-2.5 m/s2)t
t = 2.0 s
77. (B) The final velocity of the car was zero and the rate of deceleration was −7.5 m/s2 across a distance of 60 m. You can calculate the initial velocity of the car when it started skidding:
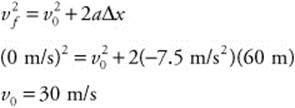
78. (A) To find the displacement, you must integrate the area under the curve to the t axis. This simply involves adding the areas of two trapezoids, one in the 0-6 s time interval and the other in the 6-10 s time interval.
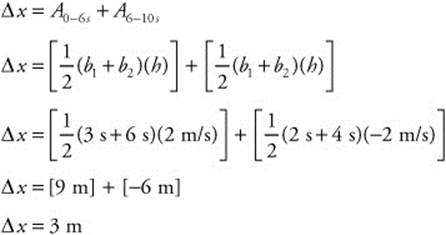
79. (B) The horizontal component of velocity is calculated by vx = v cos θ, while the vertical component is calculated by vx = v sin θ. For angles less than 45°, the cosine is larger than the sine. So, the horizontal component of velocity is larger than the vertical component.
80. (B) The dropped ball’s initial velocity was zero and it took 4 s to hit the ground. The height of the building can be calculated:
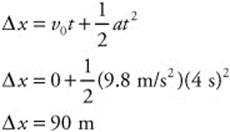
81. (D) If the positive direction is forward, then an object that is moving backward at a constant velocity would have a position-time graph that is linear with a negative slope.
82. (C) For projectiles launched at the same velocity, but at different angles (between 0° and 90°), those with complementary angles will have the same range.
83. (D) You know the initial velocity (0 m/s), the acceleration (20 m/s2), and the time (2 min = 120 s). Therefore:
vf = v0 + at
vf = (0 m/s)+(20 m/s2)(120 s)
vf = 2400 m/s
84. (B) The initial velocity of the car is 30 m/s, the final velocity is 0 m/s, and the acceleration is −9 m/s2. The distance the car traveled can be calculated:
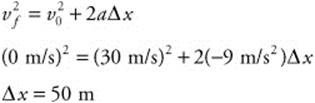
85. (C) The position in the graph is increasing nonlinearly in the positive direction. It is consistent with motion with a constant positive acceleration.
86. (B) The initial velocity of the ball is 0 m/s and the time is 2 s. The distance it travels can be calculated:
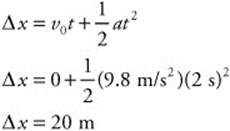
87. (D) The ice skater has an initial velocity of 10 m/s and a final velocity of 0 m/s. The time interval is 0.5 s. Calculate the rate of acceleration:
vf = v0 + at
(0 m/s) = (10 m/s) + a(0.5s)
a = −20 m/s2
88. (D) The position in the graph is increasing linearly in the positive direction. It is consistent with motion with a constant positive velocity and, hence, zero acceleration.
89. This is a projectile motion problem where v = 10.0 m/s, y = −45 m, and θ = 45°.
(a) The arrow follows a parabolic path. It first moves upward and away from the wall. It peaks and then moves downward and away from the wall until it hits the ground.
(b) The horizontal component of velocity is vx = v cos θ = (10.0 m/s) cos 45° = 7.1 m/s. The vertical component of velocity is vy = v sin θ = (10.0 m/s) sin 45° = 7.1 m/s. Because the cosine and sine of 45° are equal, the horizontal and vertical components are equal.
(c) The time it takes for the arrow to reach the ground can be calculated as follows:
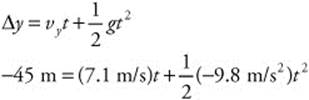
When you solve the quadratic equation by the quadratic formula, you get
t = 3.84s
(d) The range of the arrow can be calculated as follows:
Δx = vxt
Δx = (7.1 m/s)(3.84 s)
Δx = 27.3 m
90. Starting with this graph:
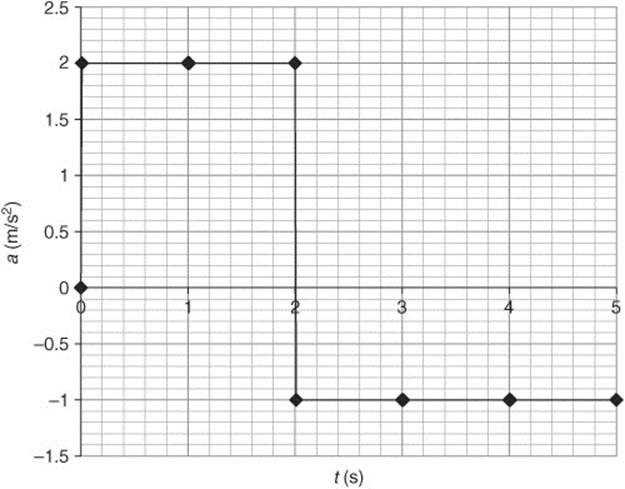
(a) Velocity is calculated by integrating the area under the curve of the acceleration-time graph (i.e., between the curve and the x axis).
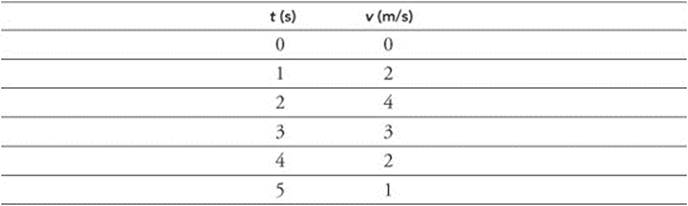
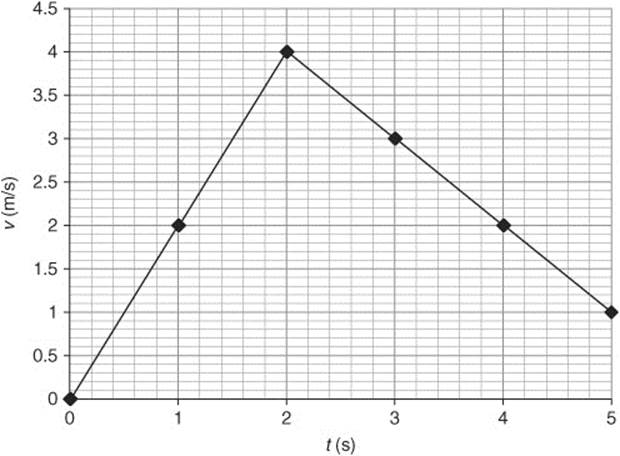
(b) The displacement intervals are calculated by integrating the area under the velocity-time graph. The position-time graph is plotted by adding the displacements.
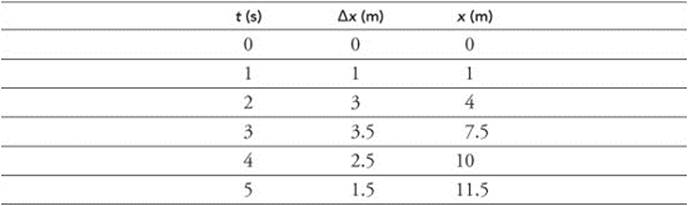
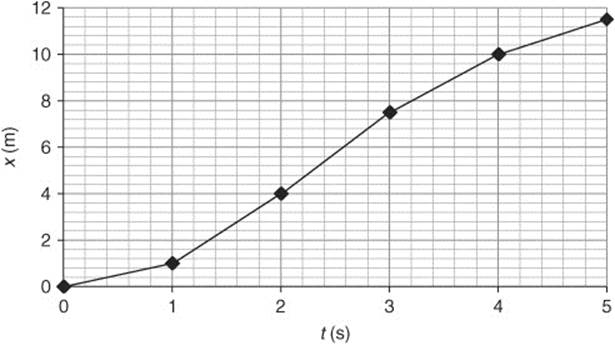
(c) The bicycle begins from rest at the starting point. It accelerates constantly for 2 s and the velocity increases linearly. The bicycle travels away from the starting point and the distance increases exponentially. From 2 to 5 s, the bicycle’s rate of acceleration decreases to a constant, but negative value. The bicycle’s velocity decreases. The bicycle continues to travel away from the starting line, but the distance gets smaller with time.
Chapter 4: Newton’s Second Law
91. (B) A 10.0-N force pushes the box to the right, while an 8.0-N force pushes it to the left. The mass of the box is 5 kg. Solve this equation for a:
Fnet = ma
(10.0 N-8.0 N) = (5 kg)a
a = 0.4 m/s2 to the right
92. (D) Remember that the force of gravity (mg) must be resolved into x and y components, and that the force of friction (Ff) is related to the normal force (FN) by Ff = μFN. The box does not move above or into the plane, so the forces in the y direction must be balanced. You can then apply Newton’s second law to both the x and y directions to come up with an expression for acceleration:
Fnety = 0
FN = mg cos θ = 0
FN = mg cos θ
Fnetx = ma
mg sin θ - Ff = ma
mg sin θ - μFN = ma
mg sin θ - μ(mg cos θ) = ma
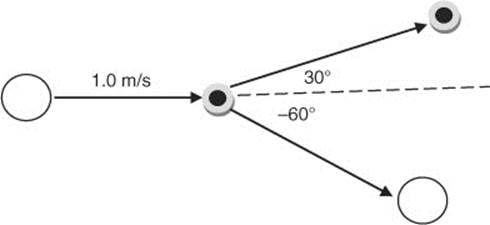
g sin θ - μ(g cos θ) = a
a = g(sin θ - μcosθ)
93. (E) The force that you exert on the rope is equal to the rope’s tension (T). The acceleration due to gravity is approximately 10 m/s2. The acceleration of the box is given at 10 m/s2 upward. Use Newton’s second law to calculate the downward force that you must apply to the rope:
Fnet = ma
T - mg = ma
T = ma + mg
T = m(a + g)
T = (10kg)(10 m/s2+10 m/s2)
T = 200 N
94. (A) You must resolve the jet’s thrust into horizontal and vertical components. Then enter the horizontal component of thrust, force of the wind, and the jet’s mass into Newton’s second law to find the acceleration:
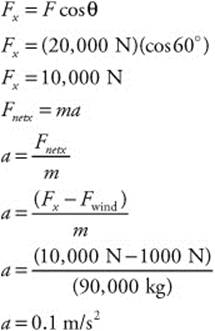
95. (C) The object accelerates only when the forces acting upon it are unbalanced. Of the choices of times listed, only 4 s and 8 s both have unbalanced forces.
96. (C) Acceleration is the second derivative of the position function. According to Newton’s second law, when acceleration is zero, there is no net force. So, calculate the acceleration function, set it to zero, and solve it for t:
First derivation: v(t) = t2-4t+3
Second derivative: a(t) = 2t-4
Set second derivative to zero and solve for t:
0 = 2t-4
2t = 4
t = 2 s
97. (D) The crate’s mass is 10 kg, one force is 10 N, and the rate of acceleration is 0.1 m/s2. You can solve for the second force by using Newton’s second law:
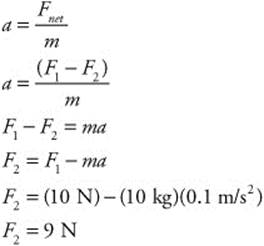
98. (C) By applying Newton’s second law to the inclined situation, you can derive an equation in which the crate’s acceleration depends only upon the coefficient of friction (μ = 0.1), acceleration due to gravity (g = 10 m/s2), and the angle of incline (θ = 45°).
Fnety = 0
FN - mg cos θ = 0
FN = mg cos θ
Fnety = ma
mg sinθ-Ff = ma
mg sinθ-μFN = ma
mg sinθ-μ(mg cosθ) = ma
g sinθ-μ(g cosθ) = a
a = g(sinθ-μ cosθ)
a = (10 m/s2)[sin 45°−(0.1)cos 45°]
a = (10 m/s2)[(0.707)−(0.1)(0.707)]
a = 6.4 m/s2
99. (B) The two masses are designated m = 5 kg and M = 10 kg. By applying Newton’s second law to the pulley system and using the direction of positive as counterclockwise, you can derive an equation for acceleration and solve the problem:
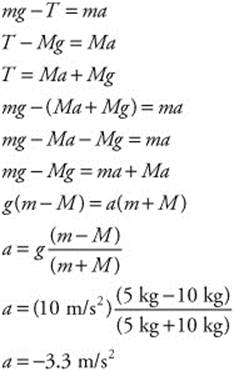
100. (A) From the graph, the acceleration at t = 1 s is −2 m/s2. The object’s mass is 5 kg. So, the net force can be calculated from Newton’s second law:
Fnet = ma
Fnet = (5 kg)(-2 m/s2)
Fnet = −10 N
101. (C) You must find the x component of the skier’s weight. The skier has a mass of 70 kg, the angle of the incline is 30°, and the skier pushes off with an applied force (FA = 105 N). Use Newton’s second law to find the rate of acceleration:
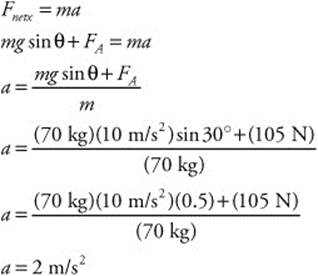
102. (B) You know the bullet’s initial velocity (0 m/s) and mass (0.010 kg). You must use Newton’s second law to calculate the rate of the bullet’s acceleration. The bullet uniformly accelerates over the distance of the musket barrel (1 m) to its final velocity:
103. (C) The second derivative of a position-time function is an acceleration-time function. When the acceleration is zero, there is no net force acting on the object. From a position-time graph, the inflection point (where the curve changes the direction of concavity) is where the acceleration is zero. For this graph that occurs at 2 s.
104. (C) The two masses are designated m = 10 kg and M = 30 kg. By applying Newton’s second law to the pulley system and using the direction of positive as counterclockwise, you can derive an equation for acceleration and solve the problem:
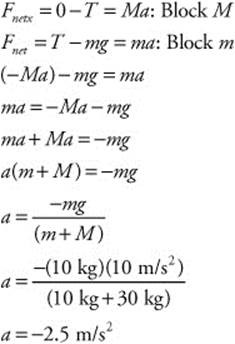
105. (C) The jet has a mass of 50,000 kg, the engines produce 20,000 N of thrust, and the acceleration is 0.3 m/s2. From Newton’s second law, you can calculate the force of the air resistance:
Fnet = ma
Fthrust - Fair resistance = ma
-Fair resistance = ma - Fthrust
-Fair resistance = Fthrust - ma
Fair resistance = (20,000 N)−(50,000 kg)(0.3 m/s2)
Fair resistance = 5,000 N
106. (E) The acceleration is the slope of a velocity-time graph. In this case, the slope of the graph yields an acceleration of 0.5 m/s2. The mass of the crate is 50 kg. From Newton’s second law, you can calculate the force applied:
Fnet = ma
Fnet = (50 kg)(0.5 m/s2)
Fnet = 25 N
107. (E) You know the initial velocity of the car (30 m/s), the final velocity of the car (0 m/s), and the distance over which the car uniformly decelerates (Δvx = 60 m). You can calculate the car’s acceleration. Once you know the acceleration and the car’s mass (1,000 kg), you can use Newton’s second law to calculate the net force on the car.
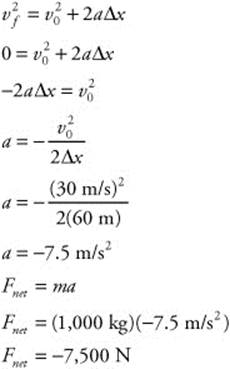
108. (D) You must first calculate the acceleration using Newton’s second law. The net force is 100 N and the mass of the ball is 5 kg. Next, you must calculate the final velocity when the ball starts from rest (v0 = 0 m/s) and the time interval is 1.5 s:
109. (B) The force of the opposing wind will cause the football to decelerate horizontally. So, the horizontal velocity will decrease. This would not be the case if there was no wind. Because the wind acts horizontally, the vertical components of the football’s path (e.g., velocity, height) will not be affected.
110. (B) The opposing forces acting upon the skydiver are gravity and air resistance. Initially, the net force is high (gravity > air resistance), the skydiver accelerates, and the velocity increases rapidly. Over time, the air resistance increases and the net force decreases. So, the acceleration decreases. At some point in time, there is no net force (gravity = air resistance), acceleration drops to zero, and the skydiver’s velocity is constant (e.g., terminal velocity).
111. (D) You know the box’s initial velocity (0 m/s) and mass (10 kg). You also know her applied force (50 N) and the force of friction opposing her (45 N). You must use Newton’s second law to calculate the rate of the box’s acceleration. The box uniformly accelerates to its final velocity of (2 m/s). You can calculate the time:
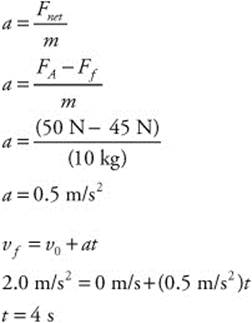
112. (E) The rocket goes from rest (v0 = 0 m/s) to 9.6 km/s (vf = 9600 m/s) in 8 min (t = 480 s). The rocket’s mass is 8.0 × 106 kg. First, determine the rate of acceleration and then use Newton’s second law to determine the net force:
vf = v0 + at
9,600 m/s = 0 m/s+a(480 s2)t
a = 20 m/s2
Fnet = ma
Fnet = (8.0 × 106 kg)(20 m/s2)
Fnet = 9.6×107 N
113. (A) The car travels at constant velocity (its value is irrelevant). So, the net force acting on the car is zero. Therefore, the force of friction is equal to the thrust of the engine (1,000 N). The mass of the car is 1,000 kg. So calculate the coefficient of friction:
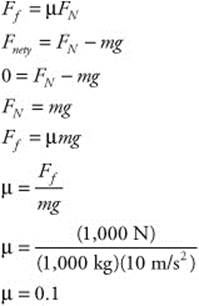
114. (B) The initial velocity of the car is 30 m/s, the final velocity is 0 m/s, and the net force acting on the car is 9,000 N. The car’s mass is 1,000 kg. Use Newton’s second law to calculate the rate of acceleration (negative as implied by deceleration). The distance the car traveled can be calculated:
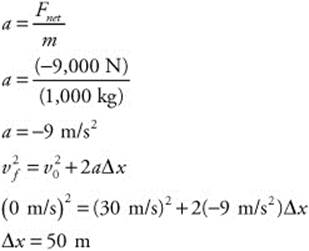
115. (D) The position in the graph is increasing linearly in the positive direction. It is consistent with motion with a constant positive velocity. The constant velocity means that acceleration is zero. According to Newton’s second law, when acceleration is zero, there is no net force acting upon it.
116. (D) The initial velocity of the runner is 0 m/s, the final velocity is 10 m/s, and the time is 0.5 s. The runner’s mass is 70 kg. First, calculate the acceleration and use Newton’s second law to find the net force:
vf = v0 + at
(10 m/s) = (0 m/s)+a(0.5 s)
a = 20 m/s2
Fnet = ma
Fnet = (70 kg) (20 m/s2)
Fnet = 1,400 N
117. (B) The ice skater has a mass of 50 kg. The force of friction acts opposite of her direction of motion (Ff = −1,000 N). Her deceleration is uniform to a final velocity of 0 m/s in 0.5 s, so you can calculate her acceleration from Newton’s second law and then find her initial velocity:
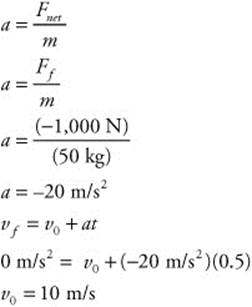
118. (C) According to Newton’s second law, the forces acting upon an object are balanced when the acceleration is zero. As shown in the graph, this occurs at 2 s.
119. This is a projectile motion problem where v = 10.0 m/s, 1y = −45 m, and θ = 45°. The arrow (m = 0.05 kg) travels against a wind in the x direction with a force of −0.05 N.
(a) The horizontal component of velocity is vx = vcos θ = (10.0 m/s) cos 45° = 7.1 m/s. The vertical component of velocity is vy = vsin θ = (10.0 m/s) sin 45° = 7.1 m/s. Because the cosine and sine of 45° are equal, the horizontal and vertical components are equal.
(b) The time it takes for the arrow to reach the ground can be calculated as follows:
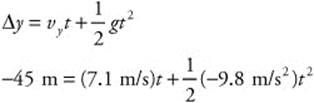
When you solve the quadratic equation by the quadratic formula, you get:
t = 3.84s
(c) While in flight, the wind exerts a constant net force of −0.05 N against the arrow. This will cause the arrow to slow down in the horizontal direction. You can calculate the arrow’s acceleration using Newton’s second law:
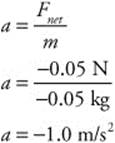
You can calculate the final velocity of the arrow:
vf = v0 + at
vf = (7.1 m/s)+(-1.0 m/s2)(3.84 s)
vf = 3.26 m/s
(c) The range of the arrow can be calculated as follows:
Δx = vxt
Δx = (3.26 m/s)(3.84 s)
Δx = 12.5 m
(d) Without the wind, the arrow would travel in the x direction with a constant velocity of 7.1 m/s. So, the range can be calculated as follows:
Δx = vxt
Δx = (7.1 m/s)(3.84 s)
Δx = 27.3 m
Therefore, in the absence of a head wind, the arrow would travel 14.8 m farther.
120. (a) The free-body diagram of this situation looks like this.
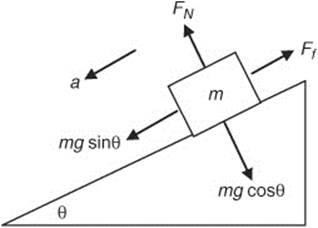
(b) We can calculate the force of friction by applying Newton’s second law:
Fnety = 0
FN - mg cos θ = 0
FN = mg cos θ
Ff = μFN
Ff = μmg cosθ
Ff = (0.1)(10 kg)(9.8 m/s2)cos 30°
Ff = (0.1)(10 kg)(9.8 m/s2)(0.87)
Ff = 8.49 N
(c) The box’s acceleration can be calculated by applying Newton’s second law:
Fnety = 0
FN - mg cos θ = 0
FN = mg cos θ
Fnetx = ma
mg sinθ - Ff = ma
mg sinθ - μFN = ma
mg sinθ - μ(mg cosθ) = ma
g sinθ - μ(g cosθ) = a
a = g(sinθ - μ cosθ)
a =(9.8 m/s2)(sin 30° - (0.1)cos 30°)
a =(9.8 m/s2){(0.5)−(0.1)(0.87)}
a =4.05 m/s2
(d) The box started from rest and accelerated down the plane for 2 s. You can calculate the final velocity:
vf = v0 + at
vf = (0)+(4.05 m/s2)(2 s)
vf = 8.1 m/s
(e) You can calculate the distance that the box moved:
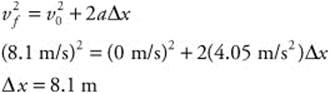
or
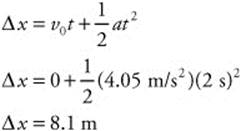
Chapter 5: Momentum
121. (E) The mass of the man is 70 kg and his velocity is 2 m/s. You can calculate his momentum as follows:
p = mv
p = (70 kg)(2 m/s)
p = 140 kg.m/s
122. (A) The force (F) applied to the hockey puck is 10 N. The time interval (Δ t) is 0.1 s. So the impulse, which is equal to the change in momentum Δp), can be calculated as follows:
Δp = FΔt
Δp = (10 N)(0.1 s)
Δp = 1.0 kg.m/s
123. (A) The mass of the car is 1,000 kg. It’s moving at a constant velocity (v = 11.0 m/s). It comes to a complete stop. So, the change in velocity (Δv = −11 m/s) occurs over a time interval (Δt = 2.0 s). You can use the impulse-momentum theory to calculate the force acting upon the car:
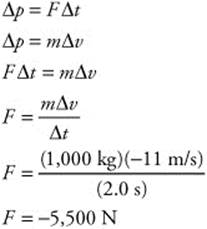
124. (B) The ball has a mass of 1.0 kg. It moves at 10 m/s. When it hits the wall, the collision is perfectly elastic. So, the ball’s direction of motion is changed and its velocity is now 10 m/s. You can calculate the ball’s momentum as follows:
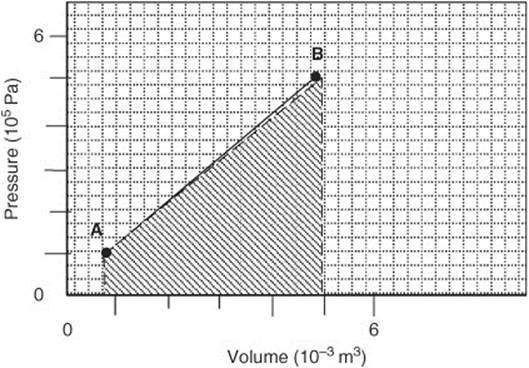
Δp = mv
Δp = (1.0 kg)(-10 m/s)
Δp = −10 kg.m/s
125. (C) The mass of the box is 10 kg and the box’s change in velocity is −10 m/s. The force applied to the box is constant at −10 N. Use the impulse-momentum theory to calculate the time it takes the box to stop:
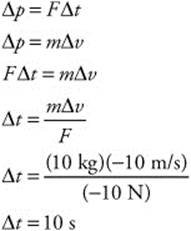
126. (D) The balls are of equal mass (mA = mB). Initially, Ball A moves at a velocity (vA) of 10 m/s, while Ball B moves at a velocity (vB) of −5 m/s. After the collision, Ball B moves with a velocity (v′B) of 3 m/s. You can calculate the final velocity of Ball A by conservation of momentum in a perfectly elastic collision:
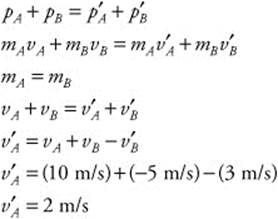
127. (D) The mass of the fullback (mA) is 140 kg, while the mass of the defender (mB) is 70 kg. Initially, A is moving at 10 m/s and B at −5 m/s. They collide inelastically because the defender wraps his arms around the fullback and they travel together. So, you can use conservation of momentum for inelastic collisions to find their combined velocity after contact:
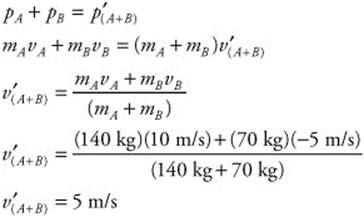
128. (E) The mass of Ball A equals the mass of Ball B, which is 200 g (mA = mB = 0.2 kg). Initially, Ball A travels at a velocity (vA) of 1.0 m/s, while Ball B is at rest (VB = 0 m/s). After the collision, Ball A is at rest (V′A = 0 m/s). The collision is perfectly elastic, so you can calculate Ball B’s velocity after the collision by conservation of momentum:
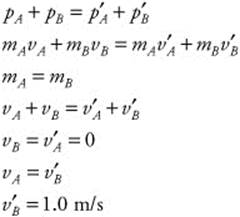
129. (E) The bullet’s mass was 50 g (0.05 kg). Its momentum was 25 kg m/s. You can calculate the bullet’s velocity as follows:
130. (C) Object 1 (m1 = 10 kg, x1 = 2.0 m) and Object 2 (m1 = 20 kg, x2 = 6.0 m) move around a common reference point. You can calculate the center of mass (xcm) of the system as follows:
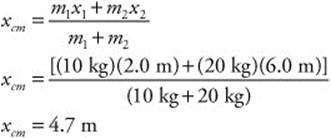
131. (A) The two masses (mA, mB) are 150 kg and 50 kg, respectively. The velocity of the halfback (vA) is 5 m/s. You must calculate the velocity that the receiver (vB) must have to stop the two of them after contact (v′A+B = 0). You can do this by using the conservation of momentum for inelastic collisions:
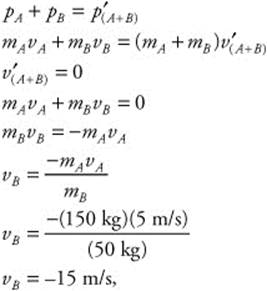
Yes, the receiver can stop the halfback.
132. (B) The bat exerts a force of 10.0 N over a time of Δt = 0.005 s when it strikes a 145-g baseball (m = 0.145 kg). You can calculate the baseball’s change in velocity by the impulse-momentum theory:
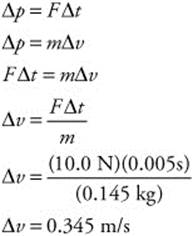
133. (D) The mass of an electron is 9.1 × 10−31 kg. The speed of light is 3.0 × 108 m/s, so 90% of the speed of light is 2.7 × 108 m/s. The momentum can be calculated as follows:
p = mv
p = (9.1 × 10−31 kg)(2.7×108 m/s)
p = 2.5 × 10−22 kg.m/s
134. (D) The mass of the cue ball is 260 g (mA = 0.26 kg), and the mass of the numbered ball is 150 g (B = 0.15 kg). The initial velocity of the cue ball is 1.0 m/s and the final velocity is zero. The initial velocity of the numbered ball is zero. The velocity of the numbered ball after the elastic collision can be found by conservation of momentum:
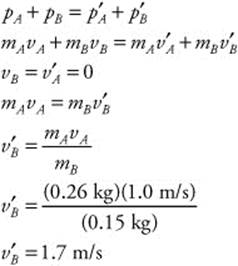
135. (A) The mass of the aircraft is 750 kg. The plane’s velocity increases from 100 m/s to 120 m/s (Δv = 20 m/s). The wind blows for 2 min (t = 120 s). You can find the force by the impulse-momentum theorem:
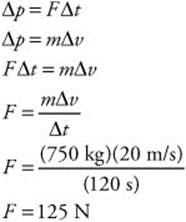
136. (C) The first derivative of a momentum-time graph is force. This is the slope of the line. In this case the slope of the line is 2. So, the force on the box is a constant 2 N.
137. (B) The force was 2.0 N and was applied for 100 m/s (ΔTt = 0.1 s). The object’s change in velocity (Δv) was 1.0 m/s. You can calculate the mass of the object by the impulse-momentum theorem:
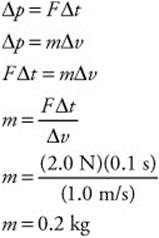
138. (D) To answer this you must find the 70-kg stuntman’s velocity when he hits the air bag. He has been free falling for 5 s, so his ν = 5t 25 m/s. He comes to a complete stop (Δv = 25 m/s) after a time interval of 2 s (2t = 2 s). You can use the impulse-momentum theorem:
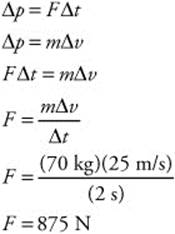
139. (B) Two railroad cars (mA = mB = 2 × 104 kg) are traveling in the same direction along a railroad track. The cars are moving at different velocities (vA = 14 m/s, vB = 10 m/s). The collision is inelastic and the velocity of the combined cars (v′A+B) can be calculated by conservation of momentum:
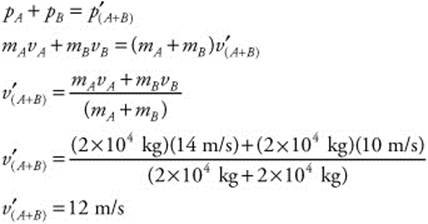
140. (C) The first derivative of a momentum-time graph is the force on the object. In this case, the derivative is a straight line with a positive slope. So, the force on the object is increasing at a constant rate.
141. (B) The masses of the skaters are 70 kg (mA) and 50 kg (mB), respectively. The total momentum before the push-off was 0. The velocity (vB) of the woman after the push-off is 2.5 m/s. You can calculate the man’s velocity by the conservation of momentum:
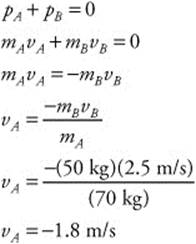
142. (D) The object’s momentum is 10 kg.m/s and its mass is 0.5 kg. You can find the object’s velocity from the definition of momentum equation:
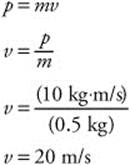
143. (E) A cue ball (mA = 250, g = 0.25 kg) travels at 1.0 m/s (Vx = 1.0 m/s, Vy = 0 m/s) and hits a numbered ball (mB = 170, g = 0.17 kg) at rest (Vx = Vy = 0 m/s). The balls move off at angles. The numbered ball moves off at 45°, while the cue ball moves off at −45°. You need to apply the law of conservation of momentum to the x components and the y components of momentum. You will get two equations that you can solve simultaneously to get each ball’s velocity:
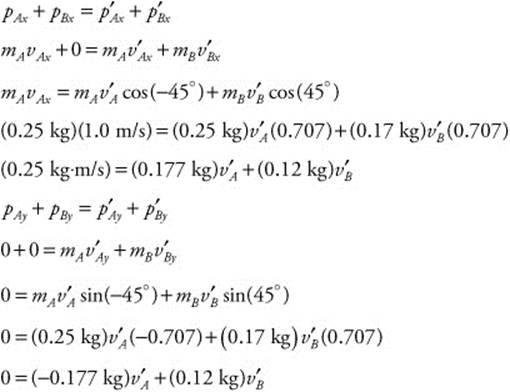
Add the two equations:
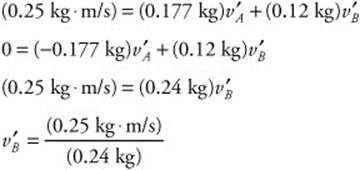
, Now substitute this value into one of the above equations:
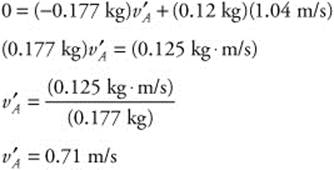
144. (E) The mass of the airplane is 2,000 kg and the velocity is 343 m/s. You can calculate the momentum:
p = mv
p = (2000 kg)(343 m/s)
p = 6.9 × 105 kg.m/s
145. (A) The mass of the handgun (mA) is 1.2 kg and the mass of the bullet (mB) is 7.5 g (0.0075 kg). The bullet travels away at a velocity (vB) of 365 m/s. You can calculate the recoil velocity of the handgun by conservation of momentum:
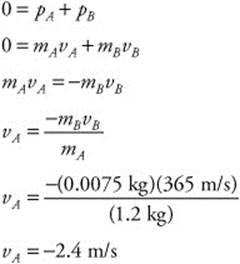
146. (D) The two cars have equal masses (mA = mB = 0.5 kg). Car A moves at 0.1 m/s and Car B is at rest (vB = 0 m/s). The two cars collide and interlock. This is an inelastic collision. You can find the velocity of the combined cars (v′A+B) by conservation of momentum:
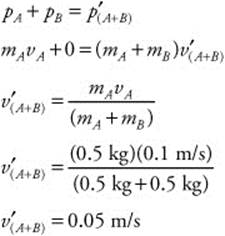
147. (C) The bullet’s mass is 4 g (0.004 kg) and its velocity is 950 m/s. The time interval that the rifle exerts on the bullet is (Δt = 0.1 s). You can find the force from the impulse-momentum theorem:
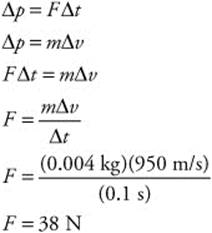
148. (C) The masses of the cannon (mA = 1,000 kg) and cannonball (mB = 15 kg) are known. The recoil velocity of the cannon (vA) is −1.5 m/s. You can calculate the velocity of the cannonball (vB) by conservation of momentum:
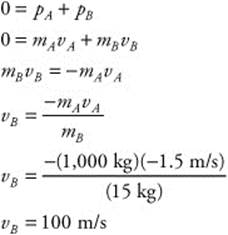
149.
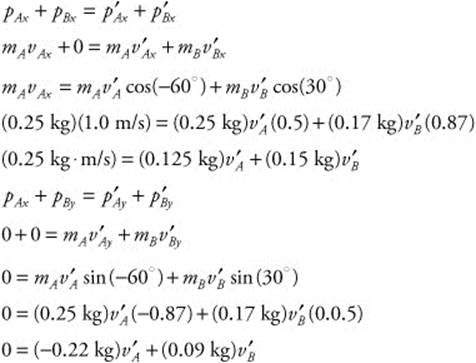
Add the two equations:
, Now substitute this value into one of the above equations:
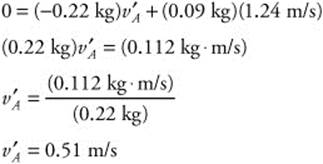
150. (a) Let’s designate Car B as the 800-kg car (vB = 25.5 m/s) and Car A as the 1,000-kg car (vA = 34.7 m/s). The two cars collide in an inelastic collision. You can find the combined velocity (v′A+B) by the conservation of momentum:
(b) Ff = μkFN
FN = (mA + mB)g
Ff = μk(mA + mB)g
Ff = (0.7)(1,000 kg + 800 kg)(9.8 m/s2)
Ff = 1.23×104 N
(c) The force of friction is negative because it opposes motion. You can calculate the time (Δt) it takes for the interlocked cars to stop (Δv = −30.6 m/s) by using the impulse-momentum theorem:
Chapter 6: Energy Conservation
151. (D) The mass of the man is 70 kg and his velocity is 2 m/s. You can calculate his kinetic energy as follows:
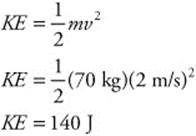
152. (D) The force (F) applied to the box is 10 N in the direction of motion. The force is applied over a 10-m distance. So the work can be calculated as follows:
W = Fd
W = (10N)(10 m)
W = 100 J
153. (C) The mass of the car is 1,000 kg. Its initial velocity is 0 m/s. The net force is 500 N and it acts constantly over a distance (d) of 100 m. You can use the work-energy theorem to calculate the car’s final velocity:
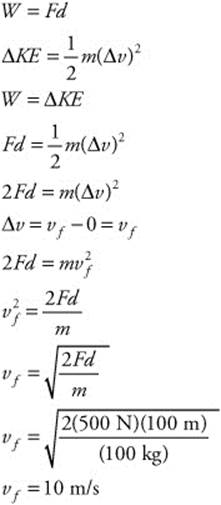
154. (C) The piano has a mass of 500 kg. Its change in height (h) is 10 m. You can calculate the piano’s change in potential energy (ΔPE) as follows:
ΔPE = mgh
ΔPE = (500 kg)(10 m/s2)(10 m)
ΔPE = 5×104 J
155. (D) The force on the box is 10 N at an angle (θ = 60°) over a distance (d) of 50 m. Only the component of force in the horizontal direction contributes to the work done on the box. You must find the x component of force and use it to calculate the work:
W = Fxd
Fx = F cosθ
W = F cosθd
W = (10 N)(cos 60°)(50 m)
W = 250 J
156. (C) The mass of the ball is 5 kg, but this information is irrelevant. The height of the hill (h) is 10 m. The ball starts from rest and reaches an unknown final velocity (v). So the ball’s change in velocity is equal to its final velocity (Δv = vf). The ball’s change in potential energy is equal to its change in kinetic energy. So, you can calculate the ball’s final velocity from conservation of energy:
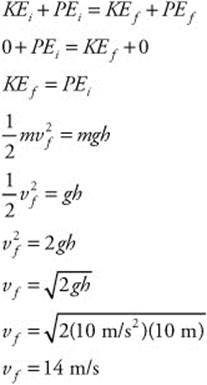
157. (C) The mass of the arrow (m) is 20 g or 0.02 kg. The archer exerts a force (F = 450 N) to pull the bowstring back (d = 1.5 m). You can calculate the final velocity of the arrow by using the work-energy theorem:
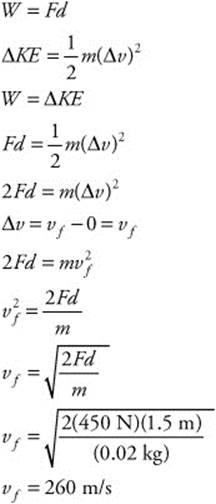
158. (E) The mass of the car is 1,000 kg. The change in velocity (v = −30 m/s) occurs over a distance (d) of 10 m. You can calculate the force by the work-energy theorem:
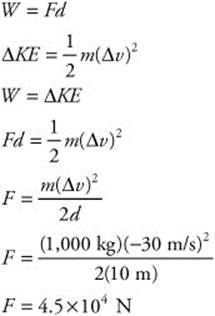
159. (E) The bullet’s mass was 7.5 g (0.0075 kg). The block’s mass was 2.50 kg. It swung to a height of 0.1 m. When the bullet strikes the wood, it is an inelastic collision. The kinetic energy of the bullet and the block get converted to potential energy. You can calculate the bullet’s velocity as follows:
First, calculate the initial velocity of the block and bullet by conservation of energy:
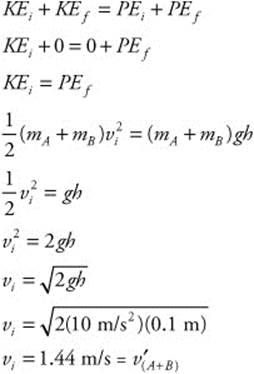
Now, use conservation of momentum for an inelastic collision to calculate the bullet’s initial velocity:
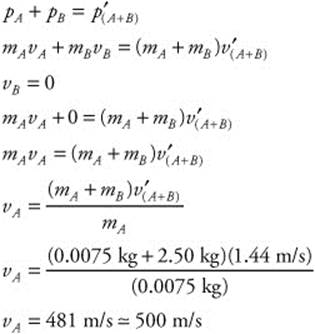
160. (B) Potential energy is the integral of force on a force versus displacement graph. By using trapezoidal integration for each 0.5-m interval, you can calculate the total potential energy:
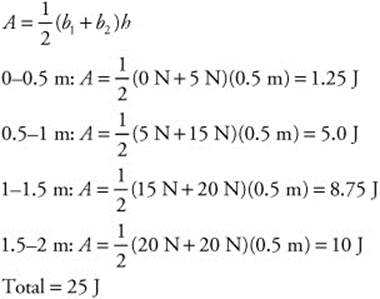
161. (C) A spring’s constant (k) is 300 N/m. The spring is stretched (x) by 0.5 m. You can calculate the force on the spring by Hooke’s law:
F = kx
F = (300 N/m)(0.5 m)
F = 150 N
162. (A) A spring’s constant (k) is 400 N/m. The spring is stretched (x) by 0.5 m. You can calculate the potential energy on the spring:
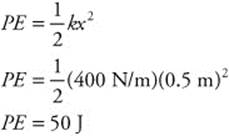
163. (D) The spring has a constant of 100 N/m and is compressed (x = −0.2 m). The mass of the block is 1 kg. You can calculate the block’s velocity as it passes equilibrium by conservation of energy:
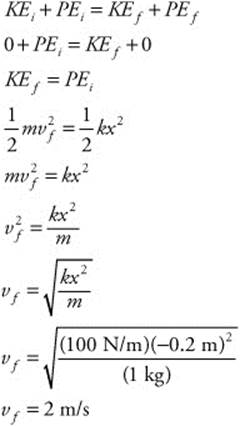
164. (C) Both cannons fire balls of the same mass (m) and use the same amount of powder to supply identical forces (F). The length of Cannon 2 (d2) is two times longer than that of Cannon 1 (d1). You can solve this problem by applying the work-energy theorem to both cannons:
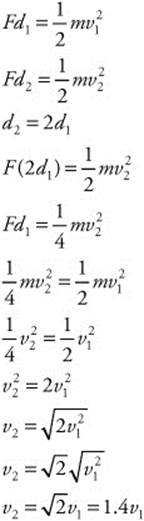
165. (A) The mass of the aircraft is 750 kg. The plane’s velocity increases from 100 m/s to 120 m/s (Δv = 20 m/s). The wind blows for 1,200 m (Δd). You can find the force by the work-energy theorem:
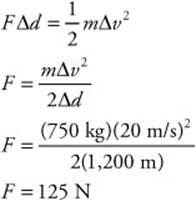
166. (D) The first derivative of a potential energy-distance graph is force. This graph has a quadratic function, so the first derivative is a straight line. From the shape of this graph, the slope of the line is positive. Therefore, the force is changing linearly with a positive slope.
167. (D) The force was 2.0 N and was applied for 5.0 m. The object’s change in velocity (Δv) was 1.0 m/s. You can calculate the mass of the object by the work-energy theorem:
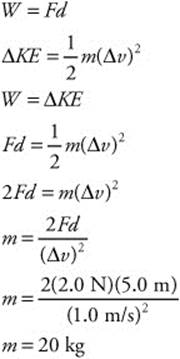
168. (C) According to conservation of energy, the potential energy of the stuntman gets converted to kinetic energy as he falls. The maximum kinetic energy occurs when he hits the airbag. The airbag must do work to stop the stuntman’s kinetic energy. So, you can solve this by applying conservation of energy and the work-energy theorem to the situation:
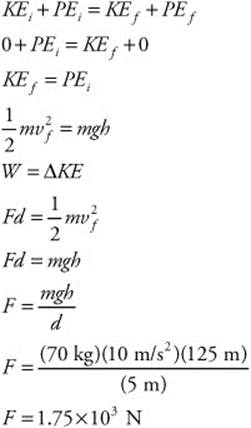
169. (E) The force exerted by the man is 100 N in the direction of motion. The mass of the box is 100 kg, which is irrelevant to the solution. The distance is 60 m and the time interval is 2 min (Δt = 120s). You can calculate the power as follows:
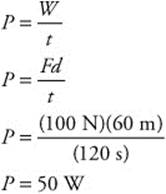
170. (E) Points A and C are at the same height and would have the same potential energy.
171. (E) The car will move the fastest at the point with the most kinetic energy, which is the lowest point, E.
172. (E) The total energy is the sum of the kinetic energy and potential energy. It is the same at all points.
173. (A) The man exerts a component (Fx) of the 20 N force (F) in the horizontal by applying the force at an angle (θ = 60°). The lawn mower moves a horizontal distance (d) of 100 m in a time interval (Δt) of 5 min (300 s). Only the horizontal component of force does work, so you must resolve the force into components and use that to calculate the power:
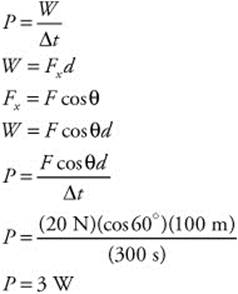
174. (D) The mass of the airplane is 2,000 kg and the velocity is 343 m/s. You can calculate the kinetic energy:
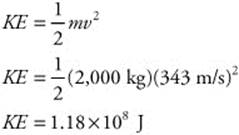
175. (D) The handgun does work on the bullet and gives it kinetic energy. All the kinetic energy (ΔKE = 500 J) is lost as heat. The length of the gun barrel is 125 mm (d = 0.125 m). You can calculate the force that the handgun exerts on the bullet using the work-energy theorem:
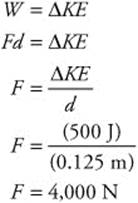
176. (D) The two cars have equal masses (mA = mB = 0.5 kg). Car A moves at 0.2 m/s and Car B is at rest (vB = 0 m/s). The two cars collide in an elastic collision. Both cars move away at 0.1 m/s. You must calculate the kinetic energies of the cars before and after the collision. Since you know that energy must be conserved, the difference between the kinetic energies before and after represents energy lost as heat. (No cars have potential energy because they are at the same height on the track.)
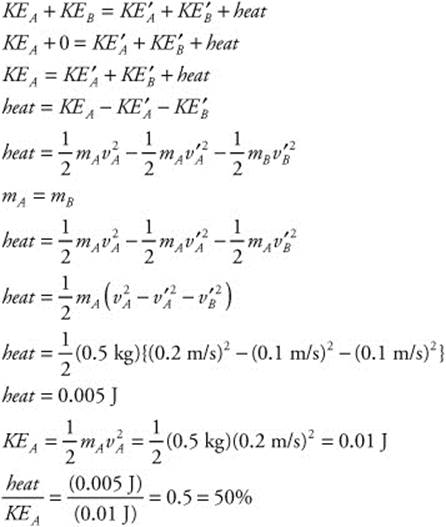
177. (C) The bullet’s mass is 4 g (0.004 kg) and its velocity is 950 m/s. The length of the rifle barrel is 1.01 m. You can find the force from the work-energy theorem:
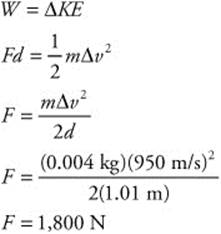
178. (C) The mass of the cannon is irrelevant. The mass of the cannonball is known (m = 11 kg). The powder charge exerts a force of 2.24 × 104 N over the length of the cannon’s barrel (d = 2.44 m). You can calculate the velocity of the cannonball (v) by using the work-energy theorem:
179. (a) You must find the height of the ramp and use conservation of energy to find the velocity of the ball:
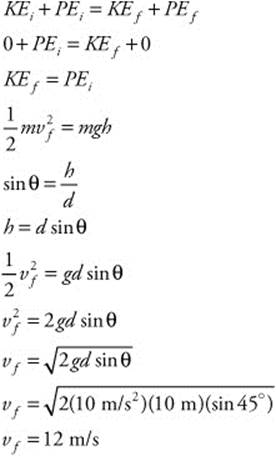
(b) Now that you know the velocity, you can calculate the ball’s kinetic energy:
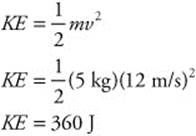
(c) The force of friction works on the ball constantly to bring it to a stop. You must first calculate the force of friction and then use the work-energy theorem to find the distance the ball travels:
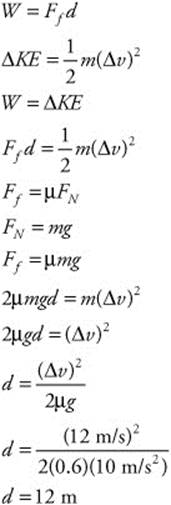
(d) You know the change in velocity of the ball and the force of friction, so you can calculate the time it takes to stop by the impulse-momentum theorem:
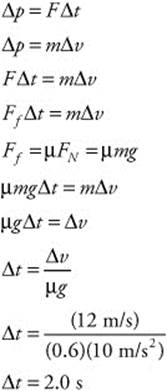
180. (a) You can determine the change in velocity of the ship by performing the following calculations:
(b) By knowing the change in velocity and the mass of the ship, you can calculate the ship’s change in kinetic energy:
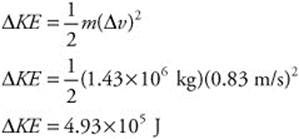
(c) First, you have to calculate the component of the force of the wind acting in the ship’s direction of motion. Then, use that to calculate the force of the wind:
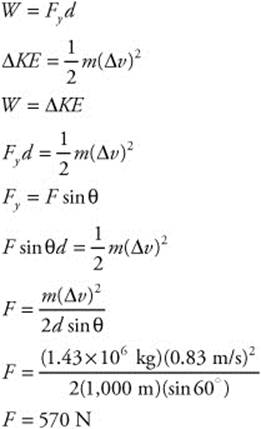
Chapter 7: Gravitation and Circular Motion
181. (C) You are given the tangential velocity of 30 m/s and the radius of the circle of 10 m. You are asked to calculate the centripetal acceleration, which is toward the center.
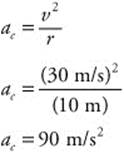
182. (D) The force of friction is what holds the car in the circular motion and is equal to the centripetal force. You calculated the centripetal acceleration in Question 181. By knowing the mass of the car (1,000 kg), you can now calculate the centripetal force, which acts toward the center.
Fc = mac
Fc =(1,000 kg)(90m/s2)
Fc =90,000 N
183. (D) You know the masses of the satellite (100 kg) and Earth (6 × 1024 kg) and the radius of the satellite’s orbit (100 km + radius of the Earth = 100,000 m + 6.4 × 106 m = 6.5 × 106 m). The value of G (6.7 × 10−11 N · m2/kg2) is implied, but it is not stated. Use Newton’s law of gravitation to find the force of gravity:
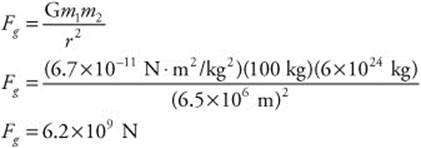
184. (E) You must compare the gravitational force on Satellite A to Satellite B using the equations of Newton’s law of universal gravitation. Note that the radius of Satellite B is twice that of Satellite A.
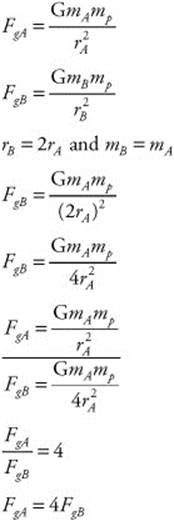
185. (A) You know the mass of the astronaut (70 kg), the mass of the spacecraft (5 × 104 kg), and the distance between them (10 m). Use Newton’s law of gravitation to calculate the force of attraction between them:
186. (A) The centripetal acceleration on the car is 1 × 105 m/s2 and the radius of the turn is 10 m. You can use the centripetal acceleration equation to find the car’s velocity:
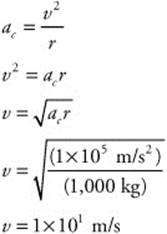
187. (A) You know the diameter of the ice rink (20 m), so you can calculate its circumference. From the circumference and the time it takes her to go around the rink once (62.8 s), you can calculate the velocity. Using the velocity, the radius, and acceleration due to gravity, you can calculate the coefficient of friction of the ice:
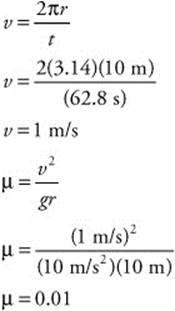
188. (C) You know the mass of the payload (1,000 kg), and the Earth (6 × 1024 kg), the Earth’s radius (6.4 × 106 m), and the height of the orbit (150 km). You can calculate the gravitational potential energy of the payload when it reaches orbit:
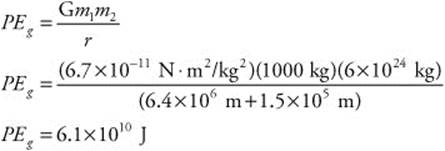
189. (B) The warrior spins a slingshot in a horizontal circle above his head at a constant velocity. When it is released, the stone will fly off at that velocity. You know the stone’s mass (50 g = 0.05 kg) and the sling’s radius (1.5 m). The tension in the string is equal to the centripetal force (3.3 N), so you can calculate the velocity:
190. (C) An acceleration of 1 G is approximately 10 m/s2. So a “3-G acceleration” would be approximately 30 m/s2. On the graph this corresponds to a radius of approximately 3 m.
191. (C) From the graph, you can see that a radius of 5 m results in an acceleration of 20 m/s2, or approximately 2 Gs. Since you know the astronaut’s mass (70 kg), you can calculate the magnitude of the centripetal force:
Fc = mac
Fc =(70 kg)(20 m/s2)
Fc =140 N
192. (D) Kepler’s third law states that the square of the period of a planet’s orbit (T) is proportional to the distance from the Sun (a) cubed. When the period is expressed in Earth years and the orbital radius in AU, then the law is T2= a3. You know that Jupiter’s orbital distance is 5 AU, so you can use Kepler’s third law to calculate its orbital period:
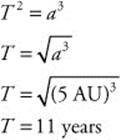
193. (C) You know the satellite’s altitude (200 km), the mass of the Earth (6 × 1024 kg), and the Earth’s radius (6.4 × 106 m). You must convert the satellite’s altitude to m and add the Earth’s radius to it to get the satellite’s orbital radius. Then, you can calculate the satellite’s velocity:
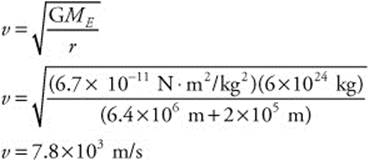
194. (D) The two masses are designated m = 10 kg and M = 30 kg. The distance between them is 2 m. So, you can use Newton’s law of universal gravitation to determine the gravitational force between them:
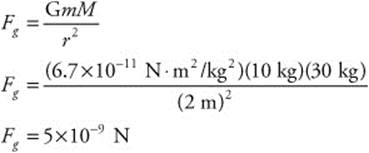
195. (E) The car’s mass is 1,000 kg, the centripetal force is 1.8 × 105 N, and the speed is 30 m/s. You can calculate the radius from the equation for centripetal force:
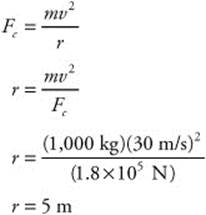
196. (E) The skater’s arm length (1 m) is the radius. She spins with a tangential velocity of 5 m/s. You can calculate the centripetal acceleration:
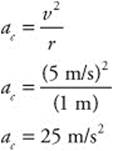
197. (B) Mars’s orbital distance is 2.3 × 1011 m. The mass of the Sun is 2 × 1030 kg and the mass of Mars is 6.4 × 1023 kg. Use Newton’s law of universal gravitation to calculate the gravitational force that the Sun exerts on Mars:
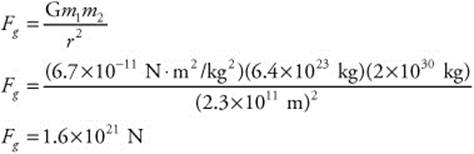
198. (D) All the coins complete a circle of rotation in the same time period. Coin D traverses the greatest circumference, so it is traveling with the fastest tangential velocity.
199. (E) If the centripetal acceleration on the space shuttle remains the same, then the orbital radius will increase with the square of the velocity. So, if the velocity triples, then the orbital radius will increase by a factor of nine.
200. (D) Pick any two points on the graph and calculate the centripetal acceleration. You must square the velocity and divide it by the radius. You will find that all of them have the same centripetal acceleration, i.e., 10 m/s2.
201. (D) The Moon’s mass is 7.4 × 1022 kg and its radius is 1.7 × 106 m. The force of gravity experienced by a 70-kg astronaut standing on the lunar surface can be calculated with Newton’s law of universal gravitation:
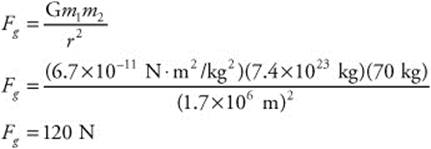
202. (B) The velocity of the wheel is its circumference divided by the period (T = 1.6 s). The wheel’s radius is 0.5 m. You can then calculate the wheel’s centripetal acceleration. Using the acceleration and the pebble’s mass (10 g = 0.01 kg), you can calculate the centripetal force on the pebble:
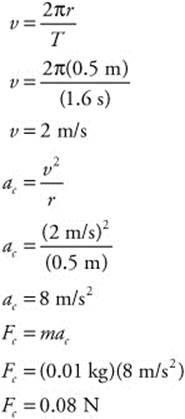
203. (B) The Moon’s mass is 7.4 × 1022 kg and its distance from the Earth is 3.8 × 108 m. The Earth’s mass is 6 × 1024 kg. You can calculate the gravitational potential energy of the Moon:
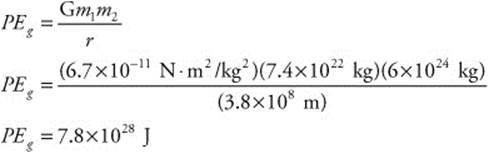
204. (D) Saturn has an orbital period of 29 Earth years. Use Kepler’s third law to determine its orbital distance:
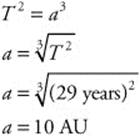
205. (B) The coefficient of friction between the rubber tires of a car and dry concrete is μ = 0.64. The radius of the turn is 10.0 m. You can calculate the maximum velocity of the car:
206. (D) The radius of the top is 2 cm. The period of the top’s spin is 0.06 s. Calculate the velocity first and then the centripetal acceleration:
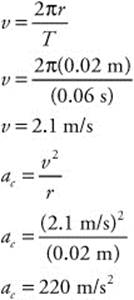
207. (B) You know the mass (100 g = 0.1 kg), the radius of the circle (2 m), and the speed (12 m/s). You can calculate the centripetal force:
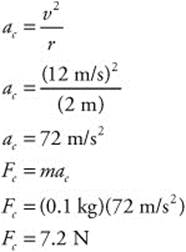
208. (B) If you apply Newton’s law of universal gravitation to each planet and the equations for each planet have constant terms, G, and the mass of the star (Ms), you find the following data about relative gravitation:
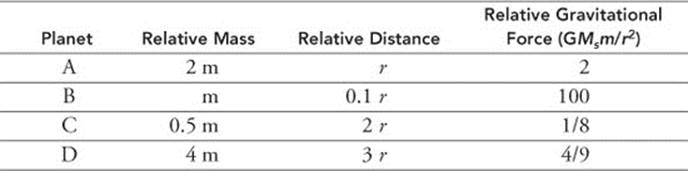
The planet with the highest gravitational attraction is Planet B.
209. You know the mass of the satellite (1,000 kg), the altitude of the orbit (1,000 km), the Earth’s mass (6.0 × 1024 kg), and the Earth’s radius (6.4 × 106 m). Use this information in Newton’s law of universal gravitation.
(a) The force of gravity on the satellite is the centripetal force on the satellite. The two are equal. The magnitude of the force of gravity is calculated as follows:
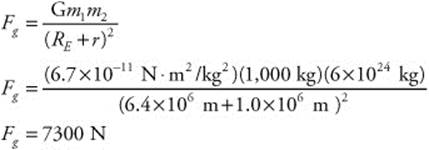
(b) Here is the magnitude of the satellite’s tangential velocity:
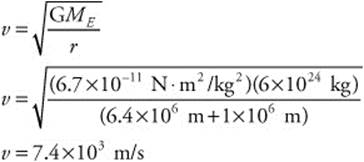
(c) Calculate the gravitational potential energy of the satellite:
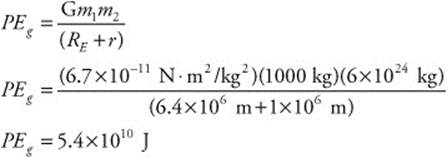
(d) Here is the value of the acceleration due to gravity (g′) at this altitude:
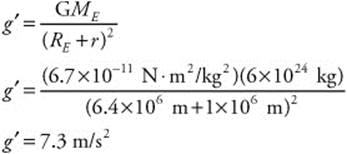
210. (a) The free-body diagram of this situation looks like the following figure:
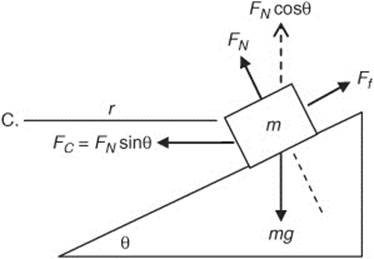
(b) We can calculate the car’s maximum velocity by applying Newton’s second law to the situation. The car’s centripetal force is provided by the horizontal component of normal force (Fc = FN sin θ = mv2/r), which is provided by the road surface. The car does not move on or off the surface of the road, so the vertical component of the normal force must balance the weight of the car (mg = FN cos θ). By dividing these two equations, we get an equation that we can solve for velocity:
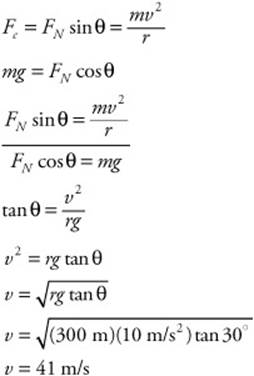
(c) Calculate the centripetal force on the car:
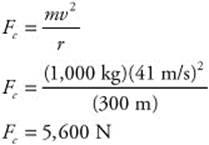
Chapter 8: Rotational Motion (For Physics C Students Only)
211. (B) R, θ, Z are the radial coordinates in a plane and the axis perpendicular to that plane.
212. (D) Rotational equivalent of mass depends on the distribution of mass and is equated to the resistance to change in angular velocity.
213. (B) Calculating its center of mass will show whether the star is rotating about its center of gravity or the center of mass of the system of one or more companions.
214. (E) The radial component of the Earth’s acceleration adds a slight amount to the gravitational attraction everywhere but the poles.
215. (C) The planets’ orbits are ellipses with the Sun at one focus.
216. (C) Mass is replaced by moment of inertia. All the equations are analogous, except that the moment of inertia replaces mass in rotational motion.
217. (D) Given that the moment of inertia of a slender rod is ML2/3, the large mass of negligible size must be included to give the total moment of inertia of the system. So the total moment of inertia is then mL2/3 + ML2. Note that the masses of the individual parts of the system are (m) and (M), and the formula for the slender rod is a general formula.
218. (A) Like balancing a seesaw, the masses must be balanced about the center of mass. So m × R1 = M × R2 applies along with L = R1 + R2. Solving these two equations yields the correct answer.
219. (D) Angular momentum must be conserved in the system, so as the skater draws his arm in to his body, he is decreasing his moment of inertia. Thus his angular velocity must increase to conserve his angular momentum.
220. (B) Unlike degrees, which are arbitrarily determined, radians are based on the properties of a circle.
221. (D) The ball flies off tangent to the circle because the string is no longer holding the ball to the circular path; therefore, the ball has a velocity tangent to the circle. At the instant the string is cut, the velocity of the ball at that moment dictates how the ball will move.
222. (B) I = m × R2. All of the mass elements are the same distance from the axis R.
I = ∫ R2dm
I = R2∫dm
I = mR2
223. (D) Although some of the other units are units of angular rotation, radians/s is the generally accepted unit.
224. (E) 7,770 m/s is given by the formula, v = R × ω, in which v is the orbital velocity, R is the radius of the junk’s orbit, and ω is the angular rotation of the junk or 2π/(90 × 60) radians/s.
225. (E) Kinetic energy of the orbiting body is dependent on the mass, its speed, and its moment of inertia. The kinetic energy = one-half × m × v2 + one-half × I × ω2. In this case, I = mR2 because the mass is small and can be considered a point mass.
226. (C) A torque is a vector because it is the cross product of a force vector and a position vector.
227. (D) We want the Earth and space platforms to be moving with the same velocity. Velocity is R × ω and set VEarth to Vspace. Solving this equation indicates that the platform should be moving at 6 radians/day, so it will remain above the Earth platform moving at 2π radians/day.
228. (C) Newton’s first law has six equations: the three for summation of forces along the three axes and the three summations of moments about the three axes.
229. (E) Using the right-hand rule, the force vector creating the torque is crossed into the position vector of the force, which gives the torque’s magnitude and direction.
230. (C) When a body is moving in circular motion, the types of acceleration acting on it are radial acceleration, tangential acceleration, and angular acceleration.
231. (D) The velocity for this case is given by 
in which v is the speed, μ is the coefficient of friction, G is the acceleration of gravity, and R is the radius of the curve. Note that the speed does not depend on the mass of the car.
232. (C) The bead’s position is a function of the speed of revolution. No matter how fast the wire spins, the bead will not get half way up the wire. The bead can move to positions below that point if the speed is fast enough. If the speed is slow enough, the bead will slide to the bottom of the axis of rotation.
233. (D) A formula for speed in circular motion is v = 2 × π × R / T in which v is the speed, R is the radius of the circle, and T is the time taken to make one circuit of the circle. Inserting all the givens into this formula yields the answer.
234. (B) At the bottom of the loop it will be moving the fastest and at the top the slowest. Gravity slows the car at the top of the loop and speeds the car to its fastest speed at the bottom of the loop.
235. (E) Gravity and radial acceleration act on the rider’s weight to produce the stated effect.
236. (C)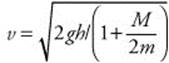 
is obtained by conservation of energy when considering the movement of the winch, the height of the anchor above the ocean floor, and the falling speed of the anchor.
237. (C) MR2/2 + MR2 uses the formula of a solid cylinder around its central axis, MR2/2. The parallel-axis theorem then adds MR2 to account for the new axis.
238. (D) 6.16 × 106 W is the result when using the power and torque formula, P = ω × τ, in which P is power, τ is the angular velocity, and τ is the torque produced by the blades.
239. In this problem, angular momentum is conserved, so the momentum of the BBs is m × v × d, where m is the mass of the BBs, v is the velocity, and d is the moment arm. This gives 0.001 kg m2/s. The target’s momentum after the hit is I × ω, in which I is the target’s moment of inertia and ω is the moment of inertia to be found. So ω = 0.001/0.015 rad/s or 0.067rad/s.
240. In this problem, the normal force of the car against the road and the weight of the car are the forces acting on the car. The car also has a radial acceleration toward the center of the curve. Newton’s second law applies to this question, so Σ Fx = m × arad and Σ Fy = 0. The normal force (N) can be broken into its x and y components based on the bank angle, B. So Newton’s equations become: N × sin B = m × arad and N × cos B + (-m × g) = 0. Solving for B, we find B = arctan arad/g or v2/(R × g) in which v is the car’s speed and R is the radius of the curve. In this case, B = 49°.
Chapter 9: Simple Harmonic Motion
241. (D) The spring’s opposing force is the vector along the incline, Mg*cosine θ. Then, from the mass/spring period formula, 
is the period of oscillation.
242. (E) The restoring force is due to the inertia of the small mass or mass ratio. The rod has a rotational spring constant of C. Then, similar to a coiled spring, the period of oscillation is 
243. (D) The pendulum swings and eventually causes the spring to oscillate. This cycle repeats in a frictionless system.
244. (B) The period of rotation is 27.3 days. Since the frequency is the inverse of the period, the period is F = 1 ÷ 27.3 days or 0.037 revolutions/day.
245. (C) Because the bell and clapper have the same period, they move as one when rung.
246. (D) The period of a pendulum depends on its length. So, by making the clapper longer, its period would be longer and out of phase with the bell. Therefore, the bell will ring with a longer clapper.
247. (E) By raising your center of gravity, you add potential energy to the system, and this causes the swing to go higher. By kicking out to the top of the swing, kinetic energy is added to the system.
248. (D) It swings in one plane. As the Earth moves under the pendulum, the pendulum demonstrates that the Earth rotates.
249. (D) It will swing until its potential energy is equal to the original potential energy, i.e., the horizontal or 180°.
250. (C) The kinetic energy in the raised ball is transferred through the balls to the only ball that can move. Thus, it rises.
251. (B) Because the pendulum’s mass moves in response to gravity, the restoring force is a function of the mass and gravity.
252. (E) The acceleration of the ship provides an artificial gravity as long as it is accelerating.
253. (A) Yes, it is moving periodically.
254. (E) It will move in a straight line tangential to where it was released and curve downward because of gravity.
255. (C) The water tank is 180° out of phase with the ship’s hull so the rolling of the ship is cancelled by the rolling of the water in the tank.
256. (B) Using the formula for the period of a pendulum, 
, the period is 16.43 seconds and the frequency is the inverse of the period or 0.06 cycles/s.
257. (D) is found by using the formula for the period of a mass spring system, 
, and by using the formula for two springs in parallel, keg = k1 + k2.
258. (B) is found by using the formula for the period of a mass spring system, , and by using the formula for two springs in series, 1/keg = 1/k1 + 1/k2.
259. (D) is found by using the formula for the period of a mass spring system, , and by using the formula for two springs in parallel, keg = k1 + k2.
260. (B) is found by using the formula for the period of a mass spring system, , and by using the formula for two springs in series, 1/keg = 1/k1 + 1/k2.
261. (D) 4.4 s for both cases. It is found by using the formula for the period of a mass spring system, 
, and knowing that both cases are frictionless.
262. (A) Determine the answer by using the formula for the period of a mass and spring system, . You also know that the three springs are parallel, so keq = k1 + k2 + k3.
263. (D) The spring constant determines the stretch of the spring, = M × g/k, and the period of a mass spring system, 
.
264. (A) The springs are supporting the compressor in parallel. Then, use the formula of frequency, 
. (Remember to convert the mass to weight.)
265. (D) Using the formula for the period of a pendulum, 
, solve for L given that T = 3.
266. (B) To answer this question, you must know the speed of light, which is 299,800 m/s. From the frequency formula, we get the period of the vibration, which is 1/6.662 × 10−11 or 1.502 × 10−12 s. This is the time it takes the light to move 1 wavelength. Multiply this period by the speed of light.
267. From the falling body equations, -x0 = v0 × t+0.5×a × t2, where x0 is zero, v0 is zero, a is the acceleration of gravity, and t is one-half of the period of the periodic motion. Because the collision of the ball with the plate is elastic, the full energy of the dropped ball is returned to the ball. So inserting t = 1 into the falling body equation and solving for x we get x = 4.9 m.
268. (D) This will allow the pendulum to oscillate and not fall over because the plate is providing a restoring force to the pendulum’s bob, which counteracts gravity.
269. Yes, it will be periodic because of conservation of energy. The ball will drop down the hole until it reaches its maximum velocity at the sphere’s center. So, its original potential energy at the surface is equal to its kinetic energy at the center. Then, its kinetic energy will carry it to the surface where its velocity will be zero and the gravitational pull of the sphere with cause the ball to fall back into the hole and so on. The ball drops 6,400 km, or 6.4 million m, to the center of the sphere. From the falling-body equations, -x0 = v0 × t+0.5×a × t2, where x0 is zero, v0 is zero, a is the acceleration of gravity, and t is one-half of the period of the periodic motion. Solving this gives T = 2586 s or 38 min.
270. The maximum and minimum amplitudes will occur when ωt is π/2 and 3π/2. The time constant is 
, which is also related to the period and frequency. Therefore, ω = 0.0005 radians/s. Using this in the period formula, T = 281 s, and the inverse of the period is the frequency, or f = .004 Hz. The maximum and minimum are equal to 20 cos π/2 and 20 cos 3π/2 or 20 cm and −20 cm.
Chapter 10: Thermodynamics
271. (D) The initial length of the railroad section is 1.0 m. The change in temperature is 15°C. The coefficient of thermal linear expansion for iron is 1.2 × 10−5°C−1. So:
ΔL = αL0ΔT
ΔL = (1.2 × 10−5°C−1)(1.0 m)(15°C)
ΔL = 1.8 × 10−4 m = 0.18mm
272. (B) You have 20 moles of a gas. The volume of the container is 1 m3 container. The temperature of the gas is 125°C. Use the ideal gas law to determine the pressure. Remember that 1 atm = 1 × 105 N/m2.
273. (C) You know the number of moles of gas (2), the temperature (25°C = 300 K), and the universal gas constant (8 J/mol · K). You can calculate the internal energy of the gas (U):
274. (D) You know the mass of an oxygen atom (5 × 10−26 kg), the temperature (25°C = 300 K), and the Boltzmann constant (1.4 × 10−23 J/K). You can find the average speed (vrms) of an oxygen molecule:
275. (B) In an adiabatic process, 0.5 moles of gas at 1,000 K expands to reach a final temperature of 500 K. You know that the process was adiabatic, so Q = 0. You also know the gas expanded and the temperature dropped, so work was done by the gas and the work value should be negative. You can calculate the work from the first law of thermodynamics:
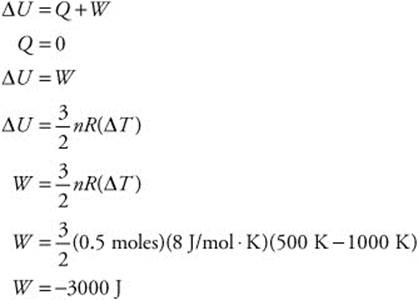
276. (C) The heat source of the engine is 5,000 J of thermal energy. The work done by the engine is 2,500 J. You can calculate the efficiency of the engine:
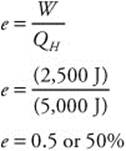
277. (C) An ideal heat engine has an efficiency of 20%. The heart reservoir has a temperature of 200°C. You can calculate the temperature of the heat sink from the ideal heat engine equation:
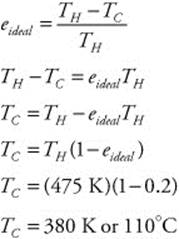
278. (B) Work is 500 J and atmospheric pressure is constant at 1 × 105 N/m2. Because work was done on the gas, the value of work must be positive. Also, because pressure was constant, the change in volume must be negative:
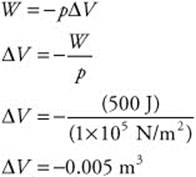
279. (A) On a pressure-volume diagram, the work done is the area under the curve; in this case, it is a trapezoid. The work was done by the gas as stated in the question, so the sign of the work must be negative:
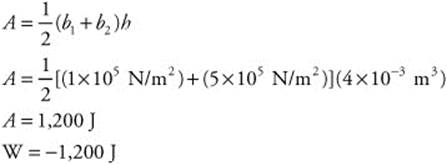
280. (D) In an isochoric process, there is no change in volume. Therefore, there is no work done on or by the gas.
281. (A) A copper rod has a diameter of 2 cm and a length of 0.5 m (the area is 3 × 10−4 m2). The rod’s temperature increases from 25°C to 50°C. The thermal conductivity of copper is 390 J/s·m·°C. You can calculate the rate of heat transfer into the copper rod:
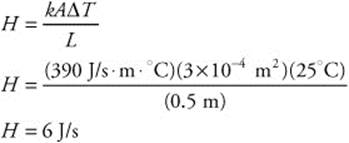
282. (A) The mass of the crate is 20 kg, the initial velocity is 0.5 m/s, the final velocity is 0 m/s, and the time is 25 s. Calculate the change in energy as the block moves, then use this value to calculate the rate of energy transfer or power:
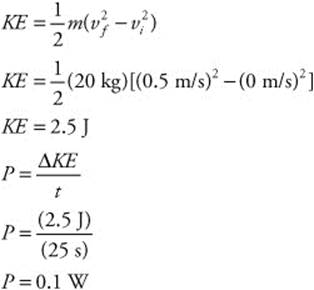
283. (D) One kJ of thermal energy (1,000 J) is transferred to a gas in a cylinder with a movable piston. At the same time, 200 J of work is done on the system. You can calculate the change in internal energy of the system from the first law of thermodynamics:
ΔU = Q + W
ΔU = (1,000 J)+(200 J)
ΔU = 1,200 J
284. (C) In an isothermal process, ΔU is zero. So, if thermal energy is added to the gas, then an equal amount of work must be done by the gas:
ΔU = Q + W
0 = Q + W
W = −Q
W = −(500 J)
W = −500 J, The gas does work as indicated by the negative sign.
285. (B) Use the following equation to determine the material that the rod is made of:
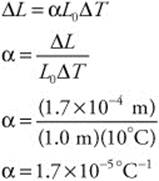
From the table, the value matches copper.
286. (D) Two moles of oxygen gas are in a container with a movable piston. The temperature is 25°C. The pressure is 6,400 Pa. Use the ideal gas equation to find the volume of the gas:
287. (E) You have 1 mole of hydrogen gas with an internal energy of 4.3 kJ (4,300 J). You can calculate the temperature of the gas:
288. (D) The engine has a 20% efficiency rating and the input thermal energy is 2 kJ (2,000 J). Use the efficiency equation to calculate the work done by the engine:
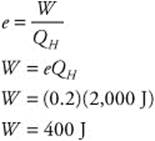
289. (E) The heat source for an ideal heat engine has a temperature of 1,000°C (1,273 K). The temperature of the heat sink is 100°C (373 K). Calculate the engine’s efficiency with the ideal heat engine equation:
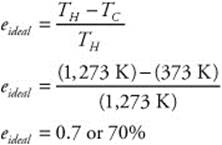
290. (A) You change the temperature of one mole of nitrogen gas from 25°C to −175°C. You can calculate the change of the gas’ internal energy. The change in energy must be negative since the temperature decreases:
291. (A) The temperature changes from 20°C to 40°C. The coefficient of thermal linear expansion for concrete is 1.2 × 10−5 °C-1. You can find the percentage change in the length of the slab:
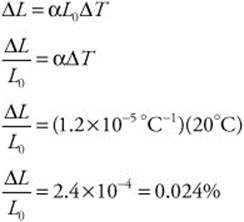
292. (C) The volume of the gas increases threefold when at a constant pressure. According to W = -pΔV, the sign of the work must be negative. This indicates the gas does work at a threefold increase.
293. (B) The volume of the cylinder is 0.001 m3, the pressure is 2,500 N/m2, and the temperature is 25°C (300 K). You can calculate the number of molecules from the Boltzmann version of the ideal gas law:
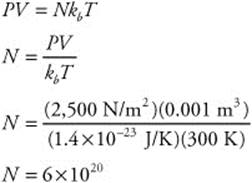
294. (E) Use the following equation to solve the question:
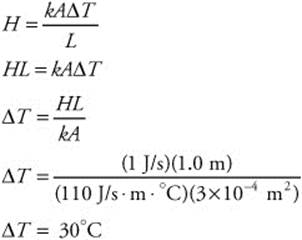
295. (E) The internal energy change during an isochoric process is 1,000 J. In an isochoric process, work is zero. Calculate how much heat was transferred using the first law of thermodynamics:
ΔU = Q + W
W = 0
ΔU = Q
W = 1,000 J
W = −500 J, the gas does work as indicated by the negative sign.
296. (E) The temperature of steam is 125°C (400 K). You can calculate the mass of a water molecule (3 × 10−26 kg) from the formula weight of water and Avogadro’s number:
297. (E) The force is 2,000 N, the piston moves 1 m, and the change occurs adiabatically (Q = 0). You can calculate the change in internal energy of the gas by using the first law of thermodynamics:
ΔU = Q + W
Q = 0
ΔU = W
W = Fd
W = (2,000 N)(1 m)
ΔU = W = 2,000 J
298. (C) An air conditioner must have work done to remove thermal energy from a cold sink to a hot reservoir.
299. (a) Work is the area under the curve (indicated on the graph).
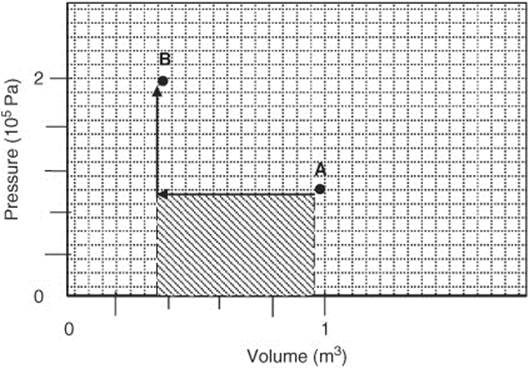
(b) First arrow indicates an isobaric compression:
W = −pΔV
W = −(1 × 105 N/m2)(0.4 m3- 1.0 m3
Second arrow indicates isochoric change in pressure
∴ W = 0
The total work is −6 × 104 J.
(c) ΔU = Q + W
Q = 0 for adiabatic process
ΔU = W
ΔU = −6 × 104 J
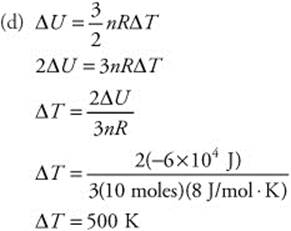
(e) ΔT = Tf - Ti
Tf = Ti + ΔT
Tf = (50 K) + (500 K)
Tf = 550 K
300. (a) ΔL = αL0ΔT
ΔL = (1.9 × 10−5°C−1)(0.1 m)(200°C)
ΔL = 3.8×10−4 m=0.38 mm
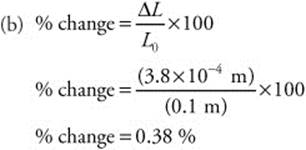
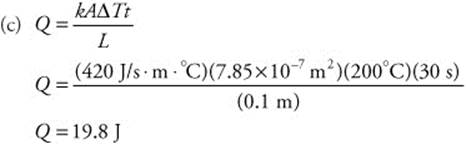
Chapter 11: Fluid Mechanics
301. (B) Using the formula of pressure = force/area, the force is 1 N, and the area is π × (0.02 m)2/4. So, the pressure in the syringe is 3,180 Pa (N/m2).
302. (C) 270,000 Pa is found from the static pressure head formula, P = δ × G × h. P is the static pressure, δ is the density of water (or 1,000 kg/m3), G is the acceleration of gravity (9.8 m/sec2), and h is the height of the water column from the top of the water level to the point of outlet, or 27.5 m.
303. (D) 620 Pa is found from the pressure formula, P = F/A, where F is the weight of the manhole cover or 50 kg × 9.8 N m/s2, and A is the area of the manhole cover or 1 m2 × π/4.
304. (D) The glass will overflow because the ice floats but displaces a volume of water to float. Since the glass is full, adding ice will overflow water from the glass.
305. (C) When Torricelli took the barometer into the mountains, the lower air density at those heights caused the mercury column to decrease. When he returned to Faenza, a low-pressure front with its usual rains had moved into Faenza. This caused the barometer to read the same as it did in the mountains.
306. (C) 18,600 N is found by multiplying the cross-sectional area of the sphere by the difference between the inside and outside air pressures. Assuming standard air pressure of 101,325 Pa, then π ×.2552× (101,325 - 10,132.5) = 18,600 N.
307. (B) When the rock is in the boat, the water level will increase because the weight of the boat and rock equals the weight of the displaced water. When the rock is dumped into the water, only the volume of the rock is displaced. Because the rock is denser than water, the water level in the pool will fall because it is only supporting the boat.
308. (A) 50,400,000 N is obtained from Archimedes’ principle wherein the buoyant force is equal to the liquid’s density multiplied by the volume submerged and the acceleration of gravity. The buoyant force must be counteracted by adding a weight that is equal to or greater than the buoyant force.
309. (D) 1.3 m is calculated using Archimedes’ principle. The salvage ship displaces 75 m3/0.5 m on the load line. So 75,600 N (volume submerged × density of sea water × acceleration of gravity) are displaced for each 0.5 m on the load line. The total load of caryatids is 200,000 N. Dividing the load by the displacement weight tells us that 2.6 displacement weights are needed to support the caryatids. On the load line this equals 2.6 × 0.5 m, or the ship rides 1.3 m lower in the water with the caryatids on board.
310. (B) A pitot tube is an instrument used to measure flow. Because of continuity, if there is 50,000 L/s at the outlet, there must be 50,000 L/s flowing anywhere in the pipeline. The velocity of the flow is affected by the diameter of the pipe. So, 50,000 L/s = 50 m3/s. Divide this by the areas of the three points in the pipe: 7.07, 3.14, 38.48 m2.
311. (D) The pump moves 5 cc of oil with each stroke. The jack cylinder is 3 cm in diameter with an area of 7 cm2. Dividing 5 cc by 7 cm2 gives the height raised with each stroke.
312. (B) 270,000 N divided by 2 m2 is 140,000 Pa.
313. (D) Use Torricelli’s law: v = h, where h is 2.75 m, and gis 9.8 m/s2. Then, the velocity is 7.3 m/s.
314. (D) Torricelli’s law can also be expressed as 
. Using the velocity from the previous problem, 7.3 m/s2, and the water’s density, 1,000 kg/m3, we solve for P, which turns out to be 27,000 Pa. The force needed to cap the outlet will be F = P/A, where A is the outlet’s area. So, the force needed to cap the pipe is 6,700,000 N, which could not be applied by a man.
315. (C) Using 
again, P is the maintained pressure, 690 kPa, and δ is the density of water, 1,000 kg/m3. Then, v is 40 m/s.
316. (B) For every 1,000 m, the water drops 0.3 m. So, 15 × 0.3 gives a pressure head of 4.5 m. Then, using the two formulas of Torricelli’s law, 
and , we can solve for P, which is 0.04 Pa.
317. Standard air pressure is 101,325 N/m2. So, the height of each column of liquid is balanced by the height of liquid in the tube. Patm = h × δ. The column heights are 10.33 m, 13.1 m, and 5.642 m, respectively.
318. (B) First, find the volume of each object from the equation, Vobj = Wobj ÷ δobj. Then, the buoyant force is the weight of the displaced water: F = Vobj × δwater
319. (D) In the same manner as Question 318, the buoyant force is 20 N × 9,807 N/m3/70,600 N/m3 or 2.8 N. Then, the amount of force needed to pull the skillet up is 20 N - 2.8 N = 17.2 N.
320. (E) Once running, there is more liquid on the downstream side than on the upstream side. The extra weight helps pull the liquid through the siphon. Some liquids can be siphoned in a vacuum.
321. (E) Once the pressure is reduced enough to allow bubbles of the liquid’s vapor to form in the siphon, then the stream is broken and it will stop.
322. (C) Water from the tank causes the water level to be above the toilet’s siphon bend and starts siphoning.
323. (D) Use the Torricelli and Bernoulli equations, h = P ÷ (δ×g), where h is the height the stream can reach, P is the pressure in the hose, δ is the mass density of the water, and g is the acceleration of gravity.
324. (E) Gravitational effects are negligible, but water vapors change throughout the atmosphere.
325. (E) The wind is funneled between the buildings and the flow is continuous, but Bernoulli’s equation of conservation of energy explains why the wind speeds up between the buildings.
326. (C) Pressure on the higher side forces the mercury up to a level at which the column’s weight equals the pressure difference. Convert 200 mm to 0.2 m. The pressure difference is then 0.2 m × 133,000 N/m3, which equals 27,000 N/m2 or 27,000 Pa.
327. (D) This can be calculated when the various accelerations are known.
328. (C) The pressure varies from 1 m to 1.25 m. So, the average depth of the porthole is 1.12 m. The pressure at this depth is h × δ × g, or 11,000 Pa. The porthole should hold under this small pressure.
329. The frequency is 
, where δ is the mass density of the water, g is the acceleration of gravity, A is the cross section of the log, and m is the mass of the log. Effectively, the log is supported by a spring that is the buoyant force on the log, or Fb = δgAh. In this case, Ah is the submerged volume of the log. Rewrite the buoyant force formula, Fb = (δgA)h, in which (δgA) is the spring constant. Then, use the formula for frequency: 
330. The liquid in a U tube oscillates around the mean level when the height of the liquid is the same on both sides. So, the displacement about the mean in a U tube is l/2 where l is the height difference used to start the oscillation. Then, use the formula for the frequency of a pendulum, 
Chapter 12: Electrostatics
331. (D) The electric charge of a proton is 1.6 × 10−19 C. The object has a charge of 8.0 × 10−19 C. So, it has five more protons than electrons.
332. (C) Only charged particles are affected by electric fields. Protons travel in the direction of the field, while neutrons travel opposite the direction of the field. So, the electron will be deflected to the left, the proton will be deflected to the right, and the neutron will pass through the field.
333. (D) The charge on an electron is −1.0 × 10−19 C and the strength of the electric field is 100 N/C. So, the force on the electron can be calculated:
F = qE
F = (-1.60 × 10−19 C) (100 N/C)
F = −1.60 × 10−19 C
The negative sign indicates that the electron moves opposite the direction of the field (i.e., to the left).
334. (D) An electron will be attracted toward the positive charge, so it takes work to move the electron from the 20-V equipotential line to the 40-V equipotential line. The work is the difference between the electrical potential at the two lines. The distance is irrelevant.
W = ΔPE =qΔV q(V2 - V1)
W = (1.6×10−19 C)(40V - 20V)
W = 3.2×10−19 J
335. (D) The charge on a proton is 1.6 × 10−19 C. The distance between them is 1 × 10−6 m. The protons have the same charge, so the force will be repulsive. Use Coulomb’s law to find the magnitude of the force:
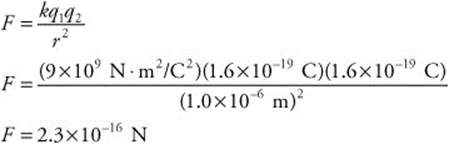
336. (E) The change in electrical potential energy (ΔEPE = PEB-PEA) is −5.0 × 10−5 J, and the magnitude of the test charge is 1 μC (1 × 10−6 C). You can calculate the voltage difference between Points A and B. Because the ΔEPEis negative, Point A must have a higher electrical potential energy than Point B:
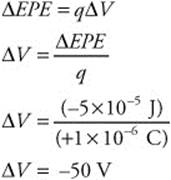
337. (D) Test Charge D is the closest to the positive point charge, so it has the greatest force acting on it.
338. (E) Charge E is the farthest away from the positive charge, so it has the greatest electrical potential energy.
339. (B) Charges A and C occupy the same equipotential line, so they have the same electrical potential energy.
340. (E) Moving Charge D to Charge E requires the most work because the force of attraction at D is the greatest.
341. (E) The separation between the parallel plates is 1 mm or 1 × 10−3 m. The voltage across the plates is 9.0 V. You can calculate the magnitude of the electric field:
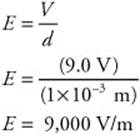
342. (A) The mass of the crate is 20 kg, the initial velocity is 0.5 m/s, the final velocity is 0 m/s, and the time is 25 s. Calculate the change in energy as the block moves, and use this value to calculate the rate of energy transfer or power:
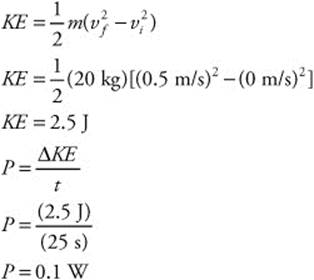
343. (B) The capacitance is 1 μF or 1 × 10−6 F. The voltage is 12.0 V. You can calculate the charge as follows:
Q = CV
Q = (1×10−6 F)(12 V)
Q = 1×10−5 C
344. (A) The area of the plates is 1 cm2 (1 × 10−4 m2), and they are separated by a distance of 1 mm (1 × 10−3 m). The permittivity of free space (ε0) is 8.9 × 10−12 C/Vm. So, you can calculate the capacitance:
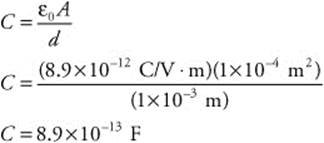
345. (C) When wires are cut through a magnetic field, the maximum flux occurs in those that are perpendicular to the direction of the field, and zero will occur in those that are parallel to the field. All others will have intermediate components based on their angle (the greater the angle, the greater the flux). In this diagram, the order of wires from least to greatest is C < E < D < A < B.
346. (D) The charge is 0.1 C and the distance is 3 m. You can calculate the voltage:
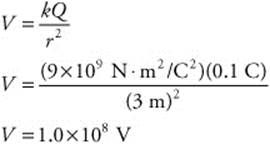
347. (E) You know the charge is 0.2 C and the force is 100 N. You can calculate the field strength:
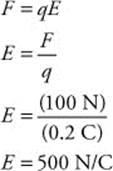
348. (E) The negatively charged object induces a charge in the neutral object. The negatively charged object repels negative charges in the neutral object to the opposite side. The remaining positive charges attract the negatively charged object.
349. (C) When placed in a uniform electric field directed to the right, only the proton will move to the right. The neutron and hydrogen atom will be unaffected, while the electron and antiproton will move to the left.
350. (D) The potential energy of the 0.05 C charge in the field is 100 J. You can calculate the voltage:
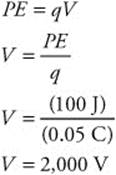
351. (B) The electric field is 900 N/C and the distance in the field from the point charge is 10 m. You can calculate the magnitude of the charge:
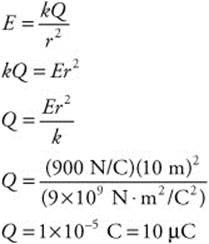
352. (B) The voltage is 120 V and the strength of the field is 1.2 × 106 V/m. You can calculate the distance (d) of separation between the plates:
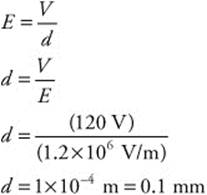
353. (B) The capacitor is 100 μF (1 × 10−4 F) and the voltage is 1.5 V. You can calculate the charge on the plates of the capacitor:
Q = CV
Q = (1 × 10−4 F)(1.5 V)
Q = 1.5 × 10−4 C
354. (B) You must first calculate the weight of the proton. Next, use the weight of the proton as the force in the electric field, and the charge on the proton to calculate the strength of the field necessary to equal gravity. The direction of the field must be upward.
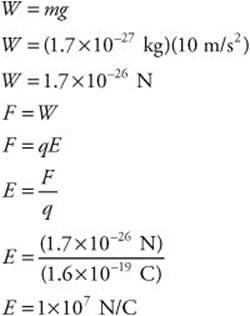
355. (C) The capacitance is 1 μF (1 × 10−6 F), the distance is 0.2 mm (2 × 10−4 m), and ε0 = 8.9 × 10−12 C/Vm.
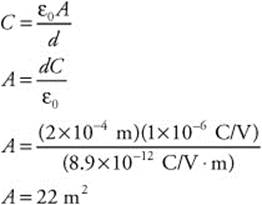
356. (D) The two electric fields will deflect any charged particles. Of the particles listed, only neutrons are uncharged and will not be affected by the electric fields. Therefore, only neutrons will hit the target.
357. (E) The electric field (10 N/C to the right) exerts a force on the charged object (q = −0.5 C, m = 1.00 × 10−3 kg). The negatively charged object will accelerate to the left. You can calculate the force on the object and then use Newton’s second law to find the acceleration:
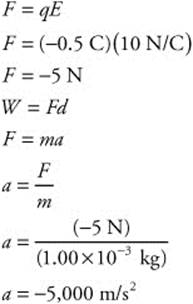
The negative sign indicates the direction of motion is opposite the direction of the electric field (to the left).
358. (C) The force on the electron is (1 × 106 N) opposite the direction of the field. The charge of an electron is (−1.7 × 10−19 C). You can calculate the magnitude of the electric field:
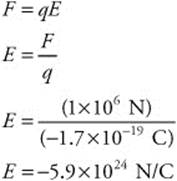
Ignore the sign of the field; it only indicates direction.
359.
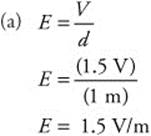
(b) F = qE
F = (1.60 × 10−19 C)(1.5 N/C)
F = 2.4 × 10−19 N
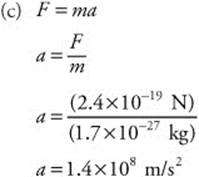
(d) vf = vi + at
vf = (0 m/s)+(1.4×108 m/s2)(1×10−6 s)
vf = 140 m/s
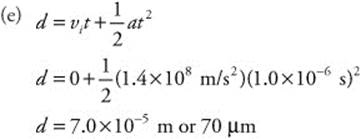
360.
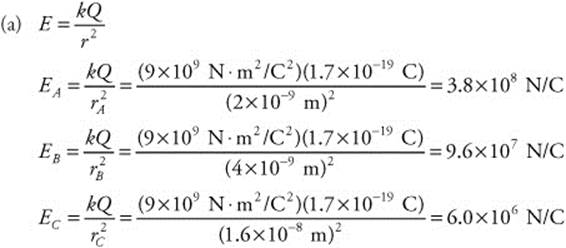
The greatest field is experienced by electron A.
The lowest voltage is experienced by electron C.
All the electrons experience attractive forces toward the protons. The greatest force is experienced by electron A.
Chapter 13: Circuits
361. (C) The electric charge is 240 C and the time interval is 10 s. Here is the current:
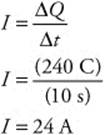
362. (A) The voltage is 9.0 V and the resistance is 10 Ω. Use Ohm’s law to find the current:
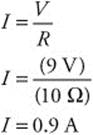
363. (E) The voltage is 9 V and the current is 3 A. You can find the power dissipated by the resistor:
P = IV
P = (3 A)(9 V)
P = 27 J
364. (C) To find the equivalent resistance of resistors in series, add all the resistances together:
Req = R1 + R2 + R3
Req = 20 Ω + 150 Ω + 500 Ω
Req = 670 Ω
365. (B) First find the equivalent resistance of the resistors by adding the resistances. Then, use Ohm’s law to find the current:
Req = R1 + R2 + R3
Req = 3 Ω + 1 Ω + 2 Ω
Req = 6 Ω
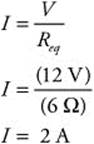
366. (E) In a series circuit, the current is equal in all parts of the circuit. However, the voltage drops across each resistor follow Ohm’s law. Since R1 has the greatest resistance, it has the greatest voltage drop across it.
367. (D) The total power dissipated by the resistors is the product of the total voltage drop (12 V) and the current (2 A):
P = IV
P = (2 A)(12 V)
P = 24 W
368. (C) Once you have found the equivalent resistance and the total current, use Ohm’s law to calculate the voltage drop across the third resistor (2 Ω):
Req = R1 + R2 + R3
Req = 3 Ω + 1 Ω + 2 Ω
Req = 6 Ω
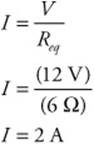
ΔV3 = IR3
ΔV3 = (2 A)(2 Ω)
ΔV3 = 4 V
369. (C) In all parts of a series circuit with different resistors, the resistances are different, the voltage drops are different, and the current is the same.
370. (D) When one light in a string of lights goes out and then they all go out, it means the lights are wired in series.
371. (D) In a parallel circuit, the current gets divided among the branches. The amount of current flow is inversely proportional to the resistance.
372. (D) The equivalent resistance of a parallel circuit is calculated as follows:
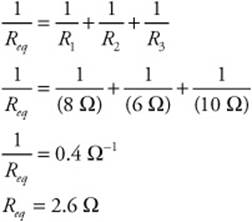
373. (B) Once you have calculated the equivalent resistance, use Ohm’s law to find out the total current:
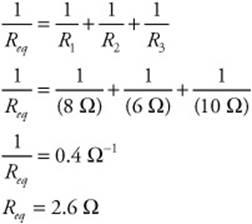
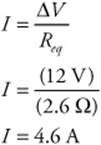
374. (B) First find the current flowing through the third resistor by using Ohm’s law and then calculate the power:
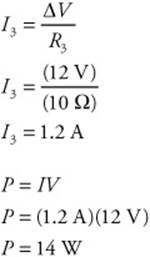
375. (C) This is a resistor-capacitor (RC) circuit. First, calculate the percent charge on the capacitor. Next, determine the time constant of the circuit, which is the product RC. Compare the percent charge to the time constant. A capacitor charges to 63% in one time constant and 87% in two time constants.
This amount of charge occurs in one time constant (RC):
τ = RC
τ = (1.00×105 Ω)(2.00×10−4 F)
τ = 20 s
376. (C) You calculate the equivalent capacitance of capacitors in series in a manner similar to calculating equivalent resistance for resistors in parallel:
377. (E) You calculate the equivalent capacitance of capacitors in parallel in a manner similar to calculating equivalent resistance for resistors in series:
Ceq = C1 + C2 + C3
Ceq = 5 µF + 4 µF + 2 µF
Ceq = 11 µF
378. (A) The voltage is 9 V and the capacitance is 10 μF. Calculate the charge on the capacitor as follows:
Q = CV
Q = (1.0×10−5 F)(9.0 V)
Q = 9.0×10−5 C
379. (C) First, calculate the current from the charge and time. Then, find the voltage from Ohm’s law:
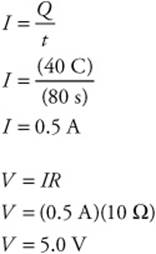
380. (E) Use Ohm’s law to find the resistance:
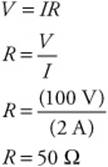
381. (C) Combine Ohm’s law and the power equation and then solve for the resistance:
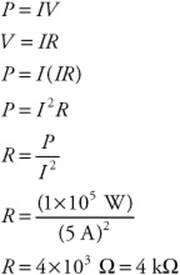
382. (A) According to Kirchoff’s laws, the sum of all the voltages around a closed loop is zero. The battery provides a 9.0 V, while the voltage decreases across each resistor [(−2.7 V) + (−4.2 V) + (−2.1 V) = −9.0 V].
383. (D) The capacitor is 10.0 μF (1 × 10−5 F). The capacitor discharges to 37% remaining charge in time constant, τ. You can calculate the resistance from the time constant:
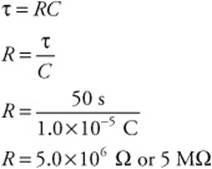
384. (E) You must first calculate the equivalent resistance of the resistors in series. Then, use Ohm’s law to find the value of the battery voltage:
Req = R1 + R2 + R3
Req = 20 Ω + 10 Ω + 30 Ω
Req = 60 Ω
V = IReq
V = (2 A)(60 Ω)
V = 120 V
385. (D) Use Ohm’s law to calculate the voltage drop across the third resistor (30 Ω) when the current is 5 A:
ΔV3 = IR3
ΔV3 = (5 A)(30 Ω)
ΔV3 = 150 V
386. (A) According to Kirchoff’s laws, the sum of all the voltages around a closed loop is zero.
387. (B) First, you must calculate the equivalent resistance of the parallel branch of the circuit 
. Then, use that to calculate the equivalent resistance of the series circuits:
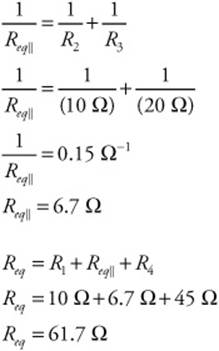
388. (B) Once you have calculated the equivalent resistance of the resistors R2, R3, and the parallel branch 
, use Ohm’s law to calculate the current moving through the circuit. That current must be equal between the first resistor, the parallel branch of resistors, and the final resistor. So, the current leaving the parallel branch must be the same as that which entered it (Kirchoff’s law):
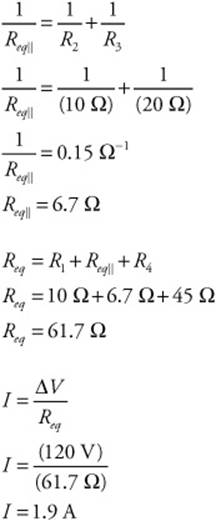
389. (a) You must calculate the equivalent resistance of the parallel branch of the circuit , then use that to calculate the equivalent resistance of the series circuits:
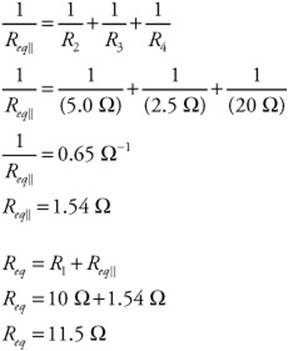
(b) Use Ohm’s law, the voltage, and the equivalent resistance to calculate the current flowing through the circuit:
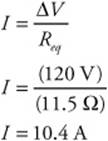
(c) ΔV = IR
ΔV1 = IR1 = (10.4 A)(10 Ω) = 104 V
ΔV2 = ΔV3 = ΔV4 (Req||) = (10.4 A)(1.54 Ω) = 16 V
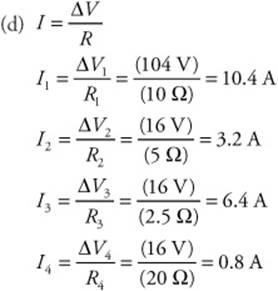
390. (a) The equivalent resistance increases linearly as you increase the number of resistors in series. In contrast, the equivalent resistance decreases exponentially as you increase the number of resistors in parallel.
(b) The total current decreases exponentially as you increase the number of resistors in series. In contrast, the current increases linearly as you increase the number of resistors in parallel.
(c) The total voltage put out by the battery remains the same as you add resistors either in series or in parallel.
(d) In the series circuit, the power decreases exponentially with increasing number of resistors. The current behaves the same way. In contrast, in the parallel circuit, the power increases linearly with the number of resistors. The current behaves the same way.
(e) As the number of light bulbs in the string increases in the series string of lights, both the current and the power of the circuit decrease. The lights appear dimmer as the number of bulbs increases. For a parallel string of lights, both the current and the power of the circuit increase as the number of light bulbs in the string increases. The lights appear brighter as the number of bulbs increase (although this happens within limits).
Chapter 14: Magnetism
391. (B) The charge of an electron is 1.6 × 10−19 C, the electron’s velocity is 1 × 107 m/s, and the strength of the magnetic field is 1.0 T. You can calculate the force as follows:
F = qvB
F = (1×10−19 C) (1×107 m/s)(1.0 T)
F = 1.6×10−12 N
392. (A) For a magnetic field to exert a force on a moving electron, the direction of the electron’s movement must have components that are perpendicular to the direction of the magnetic field. Of the angles listed, the electron moving at 0° has no component that is perpendicular to the direction of magnetic field. Therefore, the magnetic field exerts no force upon it.
393. (C) The proton moves at an angle of 30° and a speed of 5 × 106 m/s relative to the magnetic field. The field exerts a force of 4.8 × 10−13 N on the proton. You can calculate the strength of the magnetic field as follows:
394. (C) The magnetic field is directed into the paper and the velocity vector of the charge is to the right. If you apply right-hand rule no. 1, you will see that the magnetic field exerts an upward force on the charge.
395. (A) First find the equivalent resistance of the resistors by adding the resistances. Then, use Ohm’s law to find the current.
F = qvB
F = (1×10−6 C)(5×103 m/s)(10 T)
F = 5×10−2 N or 0.05 N
396. (D) If the charge shown in the figure was negative instead of positive, then the magnetic field would exert a force on the charge in the opposite direction (i.e., downward).
397. (B) By applying right-hand rule no. 1 to the charge at various positions in the circle, you can see that the magnetic field exerts a centripetal force on the charge.
398. (A) The magnetic field is directed down and the current vector is out of the paper. If you apply right-hand rule no. 1, you will see that the magnetic field exerts a force to the right on the wire.
399. (C) If the current is 10 A, the magnetic field strength is 10 T, and the length of wire inside the magnetic field is 1 cm or 0.01 m, then you can calculate the magnitude of the force:
F = ILB
F = (10 A)(0.01 m)(10 T)
F = 1.0 N
400. (D) By applying right-hand rule no. 1 to the situation, the magnetic field will exert a force on the water to the right. Newton’s third law indicates that the reaction force (thrust) is the opposite of the magnetic force. So, the thrust will be to the left.
401. (E) By applying right-hand rule no. 2 to the diagram, you see that the magnetic field comes out of the paper to the left of the wire and goes into the paper to the right of the wire.
402. (E) The point that is closest to the center of the wire (i.e., the shortest radius) will experience the strongest magnetic field. In the figure, Point E is closest to the wire’s center.
403. (C) The current in the wire is 5 A, the radius from the center of the wire is 5 mm (5 × 10−3 m), and the permeability of free space is 4π × 10−7 T · m/A. The strength of the magnetic field can be calculated:
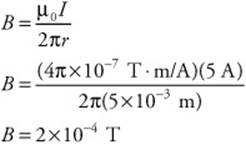
404. (B) The charge is 1 μC (1 × 10−6 C) at a distance of 5 mm (5 × 10−3 m) from the center of the wire. It is moving at 5 m/s in the same direction as the current (5 A). You can calculate the magnitude of the force:
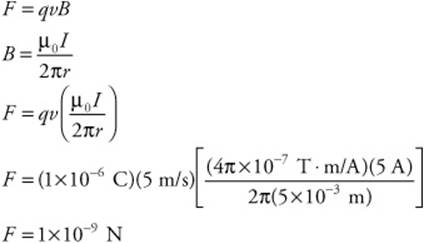
405. (C) If the solenoid has 100 coils/m and the wire carries 10 A of current, then you can calculate the strength of the magnetic field:
B = µ0nI
B = (4π×10−7 T · m/A)(100 m−1)(10 A)
B = 1.3×10−3 T
406. (D) The conducting rod (L = 2.0 m) moves at a velocity of 10 m/s. The magnetic field is 2T. You can calculate the magnitude of the electromagnetic field (EMF; e):
ε = vBL
ε = (10 m/s)(2 T)(2.0 m)
ε = 40 V
407. (A) The magnetic field is 0.5 T, and the area that it passes through is 6.3 cm2 (6.3×10−4 m2).
ϕ = BA
ϕ = (0.5 T)(6.3×10−4 m2)
ϕ = 3.2×10−4 Wb
408. (D) The number of coils (N) on one side of a transformer was 100. The magnetic flux changed at a rate of 10 Wb/s. The direction of the change was not specified, so you can only calculate the magnitude of the change using Faraday’s law:
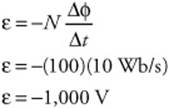
Because the direction of the changing magnetic flux was not specified, the magnitude of ε = 1,000 V.
409. (D) The magnetic field is 1 × 10−4 T. The point is 5 cm (5 × 10−2 m) away from the wire. You can calculate the current in the wire:
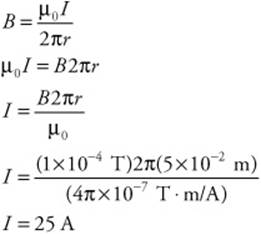
410. (C) Apply right-hand rule no. 2 to the wire on the left and you will see the direction of the magnetic field as shown in this figure. Now, the magnetic field of the left wire exerts a force on the right wire. You can determine the direction of this force by applying right-hand rule no. 1 to the left wire. You will find that the left wire exerts a force on the right wire, pushing it to the right as shown in the figure. According to Newton’s third law, the right wire’s magnetic field will push the left wire to the left. The result is that the two wires will repel each other.
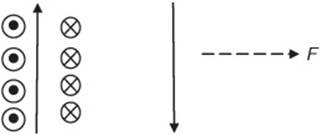
411. (B) The current is 2 A, the length of wire in the field is 10 cm (0.1 m), and the force is 0.1 N. You can calculate the strength of the magnetic field:
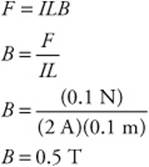
412. (A) The strength of the magnetic field is 1.0 × 1010 T and it exerts a force of 1.6 × 10−3 N on the charge. The charge is moving at 1 × 106 m/s perpendicular to the field. You can calculate the magnitude of the charge:
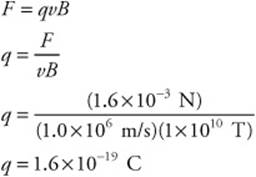
413. (A) The magnetic field produced by a wire-wrapped torus is zero everywhere outside the torus.
414. (A) By applying right-hand rule no. 2 to the figure, you can determine that the current is moving up the wire.
415. (D) The strength of the magnetic field is 5 × 10−3 T at 1 mm (1 × 10−3 m) away. You can calculate the magnitude of the current:
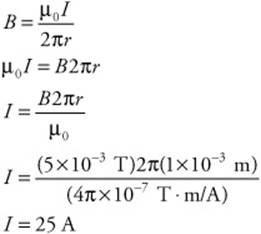
416. (D) The charge is 1 μC (1.0 × 10−6 C). It moves opposite the direction of the current at 1 cm (1 × 10−2 m) away from the center of the wire. The charge moves at a velocity of 5 m/s. You can calculate the magnitude of the force exerted on the charge by the wire’s magnetic field:
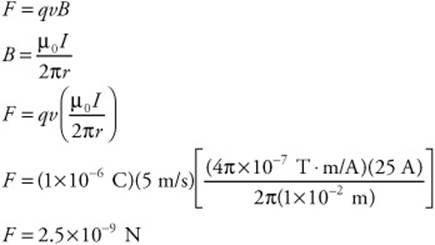
You can calculate the direction of the force exerted by the magnetic field with right-hand rule no. 1 and determine that it is away from the center of the wire.
417. (E) You can use right-hand rule no. 1 to determine the direction of the force exerted upon the charge. Remember, this is a negative charge, so the direction of the force will be opposite the palm of your hand. In this case the direction is 315°.
418. (C) The −1 μC (−1 × 10−6 C) charge moves at an angle of 45° and a velocity of 10 m/s. The strength of the magnetic field is 10 T. You can calculate the magnitude of the force exerted on the charge (ignore the sign):
F = qvB sinθ
F = (1×10−6 C)(10 m/s)(10 T)sin45°
F = (1×10−6 C)(10 m/s)(10 T)(0.71)
F = 7×10−5 N
419(a) Here’s how to calculate the magnitude of the induced EMF (ε):
ε = vBL
ε = (5 m/s)(2 T)(2.0 m)
ε = 20 V
(b) Use Ohm’s law to calculate the current flowing through the circuit:
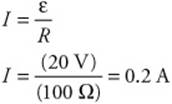
(c) The power dissipated by the light bulb can be calculated as follows:
P = Iε
P = (0.2 A)(20 V)
P = 4 W
(d) The energy used by the light bulb in 60 s can be calculated as follows:
E = Pt
E = (4 W)(60 s)
E = 240 J
420. (a) The time constant of the circuit is the time when 63% of the total current has built up (0.63 × 1.2 A = 0.76 A). Now, read the time when the current is 0.76 A to get the time constant. The value is 5 ms.
(b) Calculate the value of the inductance, L, from the time constant (5 ms or 5 × 10−3 s) and the value of the resistance (10 Ω):
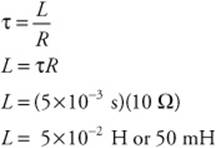
(c) Read the current from the graph at 2 τ (10 ms). The current is 1.04 A.
(d) Calculate the voltage drop across the resistor at 10 ms using Ohm’s law where the current is 1.04 A and the resistance is 10 Ω:
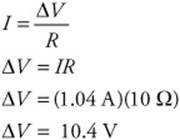
Chapter 15: Waves
421. (C) Of the waves listed, only sound is an example of a longitudinal wave in which the particles vibrate in the direction of the wave.
422. (E) The amplitude of a wave is the distance between the crest and the horizontal axis, or the trough and the horizontal axis.
423. (B) The period of a wave whose frequency is 100 Hz can be calculated as follows:
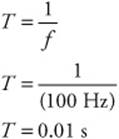
424. (D) Here’s how to calculate the velocity of a wave with a frequency of 100 Hz and a wavelength of 1.0 m:
v = fλ
v = (100 Hz)(1.0 m)
v = 100 m/s
425. (D) A sound wave travels at 343 m/s. The wavelength of the sound wave is 17.2 cm (1.72 × 10−2 m). You can calculate the frequency:
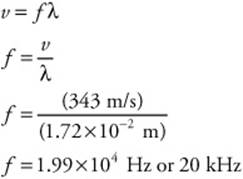
426. (C) The sound wave broadcast through the headphones is 180° out of phase with the one from the jackhammer. The two waves interfere with each other and cancel out. The result is that the operator does not hear the jackhammer noise. This is an example of destructive interference.
427. (D) The length of the open tube is 0.5 m. The speed of sound at 20°C is 343 m/s. You can calculate the fundamental frequency of the tube (n = 1):
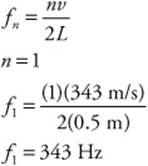
428. (B) The wavelength is 475 nm or 4.75 × 10−7 m. The spacing in the diffraction grating is 0.5 mm or 5 × 10−4 m. The screen is 2 m away. Here’s how to calculate the distance from the center spot (x):
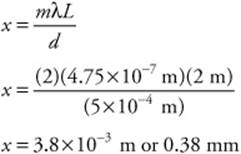
429. (C) The wavelength of light entering the material is 510 nm, while the wavelength of light within the material is 638 nm. You can calculate the index of refraction of the material:
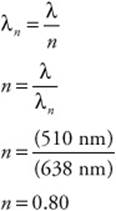
430. (D) Maxwell’s third equation is Faraday’s law.
431. (D) The two waves will add together and the resulting wave will have the amplitude 2A/3.
432. (C) The figure depicts the phenomenon of destructive interference.
433. (D) After the waves meet, they will travel on as depicted in the diagram. One wave (+A) will travel to the right, while one wave (−A/3) will travel to the left.
434. (B) The frequency of the tuning fork is 440 Hz. At the temperature specified, the speed of sound is 343 m/s. We are looking for the length, L, of the air column when the first (n = 1) resonance sound is heard.
435. (C) The tsunami wave’s velocity is 720 km/h (200 m/s). The period of the wave is 10 min (600 s). You can calculate the wavelength:
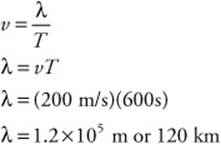
436. (E) According to Maxwell, only accelerating charged particles will produce an electromagnetic wave (i.e., light). An accelerating proton is such a particle.
437. (B) The wavelength of light entering the gasoline is 590 nm. The index of refraction of gasoline is 1.4. You can calculate the wavelength of light within the gasoline:
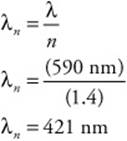
438. (B) The speed of light, c, in a vacuum is 3.0 × 108 m/s. The index of refraction, n, of the glass is 1.5. You can calculate the speed of the light wave within the glass:
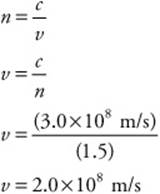
439. (B) A monochromatic light wavelength of 500 nm passes through a 5-μm slit and produces an interference pattern on a screen. You can calculate the angle from the slit where you would find the fifth spot (m = 5) from the center:
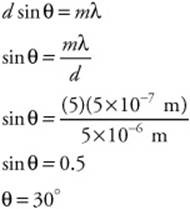
440. (B) Of the EMF waves listed, radio waves have the lowest frequency and longest wavelengths.
441. (A) The speed of a radio wave is the speed of light (3 × 108 m/s) and the frequency is 100 MHz (1 × 108 Hz). You can calculate the wavelength of the radio wave:
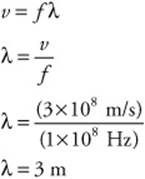
442. (D) The change in frequency of a wave emitted from a moving object as that object passes you is called the Doppler effect.
443. (A) The pipe length is 3 m and is closed at one end. You can calculate the frequency of the third harmonic (n = 3):
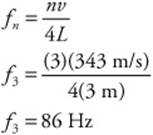
444. (B) The beat frequency is the difference between the two frequencies of the tuning forks (440 Hz - 320 Hz = 120 Hz).
445. (A) The medium above the top surface of the soap film and that below the bottom surface are identical. In this instance, there is only one phase reversal in the waves that are reflected from the top and bottom surfaces of the film. So, constructive interference occurs when the extra distance traveled by the ray through the film is one-half the wavelength of within the film (λn). Therefore, with an index of refraction, n, of 1.5 and a wavelength of 600 nm perpendicular to the film, solve for the minimum thickness of the film at which constructive interference occurs:
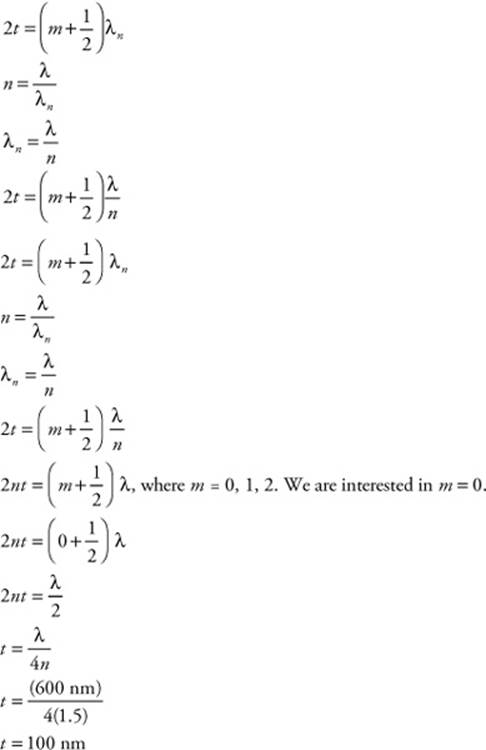
446. (C) The two waves will add together and the resulting wave will have the amplitude 3A/2.
447. (E) A wavelength can be measured either from crest to crest or trough to trough.
448. (C) The light travels through the water at a velocity of 2.26 × 108 m/s. You can calculate the index of refraction of the water:
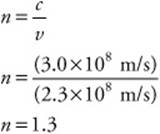
449. (a) The relationship between the order number and the distance from the center of the spot is linear (this is shown in all of the graphs). For any given wavelength and slit spacing, the interval between each spot is constant.
(b) As you increase the spacing between the slits, the distance of the spots from the center decreases (i.e., the spots get closer together). This relationship is shown in Experiment 1. The slit spacing is probably the most influential factor in determining the separation of the spots.
(c) As you increase the wavelength, the spacing between the spots increases. This is shown in Experiment 2.
(d) The data from Experiment 1 shows that decreasing the slit spacing will increase the spacing between diffraction bands (spots for lasers). For example, a diffraction grating with a small spacing (on the order of 1-100 μm) will give a good separation.
450. As the light ray passes through the oil film, there are two phase reversals, one between air and oil and the other between oil and glass. So, destructive interference occurs (i.e., the blue light gets subtracted out) when the extra distance traveled by the ray through the film is one-half the wavelength of within the film (λn). Therefore, with an index of refraction, n, of 1.3 and a wavelength of 475 nm perpendicular to the film, solve for the minimum thickness of the film at which constructive interference occurs:
Chapter 16: Optics
451. (D) Red, orange, yellow, green, blue, and violet.
452. (C) With the indices the same, light is not refracted, and the glass is not seen.
453. (A) 50 cm is obtained from f = R/2.
454. (D) The focal length is one-half of the radius of curvature or 4 km. The reflected light would have to be focused on the ships at sea 2 km away. Given the ancient Greeks’ knowledge of geometry, they could very likely make such mirrors.
455. (B) This type of lens would move the eye’s focal point back toward the retina from inside of the eye.
456. (C) This can be done using two lenses of different refractivity such as a convex-convex crown glass lens mated with a concave-concave flint glass lens.
457. (D) Because of the law of reflection, the reflected beam comes off at the same angle as the incident beam.
458. (D) A matte surface would diffuse the laser beam and minimize the likelihood of burning something or causing an injury.
459. (C) This is because the line of sight of the fish bends slightly away from normal when it moves from water to air.
460. (D) It should be lower than that of the fiber so that total reflection can take place.
461. (D) All of the answers are correct.
462. (E) The magnification is found from dividing the object lens’s focal length by the eyepiece’s focal length, so that the magnification = 980/50 = 19.6.
463. (E) Newton’s telescope did not eliminate spherical aberration.
464. (D) The lack of atmospheric aberration contributes to the clarity of the image.
465. (D) It is above much of the atmosphere and has low light pollution, but it only views the Southern Hemisphere. It is also in a desert with low humidity and is electronically connected to far-away astronomers.
466. (E) Shorter wavelengths are refracted more than longer wavelengths.
467. (B) An image in a mirror will appear as far behind the mirror as the object in front of it. Theoretically, there should be an infinity of images with two parallel mirrors going into the distance in the mirror. But, because of the resolution power of the eyes, there will be a point at which the reflected image will be too small to be seen.
468. (B) Using the mirror formula, 1/p + 1/q = 1/f = 2/R, p is considered to be infinity and thus the star images will appear at the focal length 200 cm.
469. (C) This lens will bring the eye’s focal point back to the retina from behind the eye.
470. (E) A cylindrical lens is asymmetric and can be used to correct for aspherity in the eye.
471. (E) A one-way mirror works because the observers’ room is darkened, the person being observed is brightly lit, and the observer side of the mirror is only partially silvered. All three conditions must be met. Glass does have a large index of refraction.
472. (C) Drops of water act like lenses and focus the sun on the leaf. Thus causing it to burn and turn brown.
473. (B) A cat’s eyes are mirrored.
474. From the geometry, the observer’s line of sight when the cup is empty forms the hypotenuse of a right triangle with sides, d (depth of cup), and 6 cm (diameter of the cup). The hypotenuse also forms the angle, α, with the side of the cup. Similarly, when the cup is filled with water, the observer’s line of sight is refracted by the water and forms the hypotenuse of another triangle with sides d and 3 cm. Let the refracted angle with the wall of the cup be β. Then, use the Pythagorean theorem, sin 
and sin
. Then, use the laws of refraction, sin
. When this ratio equals 1.333, the refractive index of water, d, is 3.05 cm.
475. Using the lens equation, 1/dobj + 1/dim = 1/f, f and dobj are known and so dim can be found. They are respectively 30 cm, 40 cm, ∞, −20 cm, and −6.7 cm.
Chapter 17: Atomic and Nuclear Physics
476. (C) Divide the critical mass by the density to get the volume. Find the diameter of the sphere from the formula for the volume of a sphere.
477. (A) The naturally occurring radioactive elements are: technetium, promethium, polonium, astatine, radon, francium, radium, actinium, thorium, protactinium, uranium, and neptunium. The manmade elements are plutonium, americium, curium, berkelium, californium, einsteinium, fermium, mendelevium, nobelium, lawrencium, rutherfordium, dubnium, seaborgium, bohrium, hassium, meitnerium, darmstadtium, roentgenium, copernicium, ununtrium, ununquadium, ununpentium, ununhexium, ununseptium, and ununoctium.
478. (B) They make up a helium nucleus, an electron, and a photon.
479. (B) A helium nucleus, an electron, and a photon.
480. (E) 15 × 108 J is found from E = mc2.
481. (D) 92, 92, 143 in which the atomic number, 92, provides the number of electrons and protons, and the atomic number subtracted from the isotope number yields the number of neutrons.
482. (D) The energy in a photon is given by the equation h × c/λ, in which h and c are constants. The wavelength, λ, is the only variable. The frequency, while variable, also depends on the wavelength.
483. (C) Half-life is the period of time it takes for a substance undergoing decay to decrease by half. A simple formula for this is:
N is the quantity of the substance that varies with time, t is the variable time, and t1/2 is the half-life of the substance.
484. (A) Alpha particles contain two protons and two neutrons. To reduce the atomic weight from 238 to 206, eight alpha particles must be emitted, which remove 32 neutrons and protons.
485. (B) 2.02 eV is found by using the equation for the energy of a photon, E = h × c/λ, and noting significant figures.
486. (D) The slow neutron has no charge and can hit the nucleus to cause fission, while a slow proton has a positive electric charge and is repulsed by the much larger positive charge of the uranium nucleus.
487. (D) Most elements are a mix of isotopes with more or less neutrons than predicted by the atomic number subtracted from the amu. The neutrons account for the fractional amus.
488. (E) The electron and positron are of opposite charge and annihilate each other by emitting two photons to conserve energy.
489. (B) An alpha particle is 2helium4 with no electrons. When 7nitrogen14 is bombarded, the elementary particles are conserved and usually stable isotopes are produced. In this case, 1hydrogen1 is produced so the remaining neutron and proton must go to produce 8oxygen17. 1hydrogen3 is radioactive 1tritium3; 1hydrogen2 is radioactive 1deuterium2, making (A) and (C) wrong. In (D) and (E) the numbers do not add up correctly.
490. (D) The energies are calculated from the energy of a photon equation: E = h × c/λ, while 1 eV = 1.6 × 10−19 J/eV accounts for the units.
491. (D) There are 6.022 × 1023 atoms/mol of substance. The mass of 1 mol equals the atomic mass of the element, in this case 235 g or 0.235 kg. One eV is equal to 1.6 × 10−19 J. Then the number of atoms, multiplied by the energy emitted, divided by the atomic mass gives the result when units are accounted for.
492. (B) One eV is equal to 1.6 × 10−19 J/eV. An electron has a mass of 9.11× 10−31 kg. The kinetic energy of the electron is 1.6 × 10−19 J. From the kinetic energy the velocity can be calculated by kinetic energy = one-half × m × v2. Solving for v yields 5.93 × 105 m/s when accounting for the units.
493. (B) A photon is a quantum of energy, which allows the effect.
494. (C) Although it also was related to the other answers, (C) was the most important.
495. (C) Light behaves like a wave or a particle depending on which property is being examined. This is a mathematical construct to allow examination of the phenomenon of light and its interaction with the natural world.
496. (D) Neutrons hitting atoms cause fissions. These can be regulated by neutron absorbers.
497. (D) Most elements can be split, but some like hydrogen and helium cannot because they do not have the proper number of particles to cause alpha-particle emission.
498. (E) In beta decay, the atom’s charge and kinetic energy must be conserved. So depending on the type of beta decay, a neutron turns into a proton with emission of an electron. Similarly in beta decay in which a positron is emitted, a proton turns into a neutron to maintain the proper charge. During beta decay a neutrino and an antineutrino are emitted to conserve the system’s kinetic energy.
499. We are given the radius of the universe shortly after the Big Bang: converted to centimeters it is 1.5 × 1013 cm. The volume of a sphere is 0.75 × Π × r3, where r is the radius of the sphere, which in this case is 1.5 × 1013 cm. So, the volume is 3.53 × 10−30 cm3. We can calculate the average mass of the three particles, (P + N + e)/3, or, when converted to grams, (1.67 × 10−30 g + 1.67 × 10−30 g + 9.11 × 10−33 g)/3 = 1.11 × 10−30. We were given the mass density of the sphere shortly after the Big Bang to be 1015 g/cm3. Finally, we can divide the mass density by the average particle mass to get the number of particles in the sphere, or 1.41 × 1049/1.11 × 10−30 = 1.27 × 1079.
500. 9.4 × 1019 fissions/s and 2.88 × 10−3 kg/day. A watt is a J/s. So, 3.000 × 106 J/s = X number of fissions, × 200 × 106 eV per fission, × 1.6 × 10−19 J/eV yields: 9.4 × 1019 fissions/s. From E = mc2, 3.000 × 109 J/s = X kg × (3.00 × 108)2. Solving for X = 3.000 × 109 J/s 60 s/m × 60 s/m × 60 m/hr × 24hr/day/ (3.00 × 108)2 yields 2.88 × 10−3 kg/day.