5 Steps to a 5: AP Physics 2: Algebra-Based 2024 - Jacobs Greg 2023
STEP 2 Determine Your Test Readiness
5 Test Yourself: AP Physics 2 Question Types
IN THIS CHAPTER
Summary: In the last chapter you analyzed your basic content knowledge. In this chapter you will test yourself with the types of questions you will encounter on the AP Physics 2 exam itself. If you have taken the AP Physics 1 exam, you will already have some experience with these types of questions. Practice makes perfect. A complete key to the practice questions can be found at the end of the chapter.
Key Ideas
Content knowledge is only the first step. You need to know how questions will be organized and what they expect.
Some question types will be new to you. Become familiar with their format.
This self-assessment, and the fundamentals self-assessment from Chapter 4, will help you develop a study plan that matches your unique needs (Chapter 3).
AP Physics 2 Question-Types Self-Assessment
The AP Physics 2 exam has many different question types including:
• Descriptive problems
• Calculation problems
• Ranking tasks
• Experimental description and analysis questions
• Multiple questions referring to the same stem
• Multiple-correct questions
• Experimental design free-response questions
• Qualitative-quantitative free-response questions
• Paragraph length argument free-response questions
Some of these may look familiar, while others will seem new or perhaps even odd. I don’t want you to be surprised while taking the AP exam. Practice these problems to find which are easy for you and which ones are a struggle. Adjust your study plan accordingly (Chapter 3). Chapters 6—8 give strategies for handling the question types you will encounter.
Descriptive Problems (No Numbers)
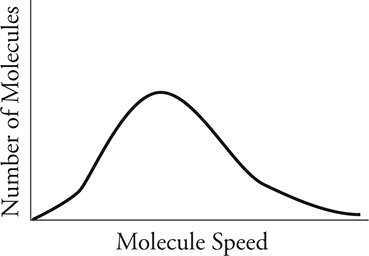
1. The graph shows the distribution of speeds for 1 mole of helium at temperature T, pressure P, and volume V. How would the peak of the graph change if the sample was changed from 1 mole of helium to 1 mole of hydrogen at the same temperature, pressure, and volume?
(A) The peak will shift to the left.
(B) The peak will shift upward and to the left.
(C) The peak will shift to the right.
(D) The peak will shift downward and to the right.
2. Four equally spaced charges of the same magnitude are arranged as shown in the figure. At which location is the electric field directed to the right?
Semiquantitative Reasoning (No Numbers but the Relationships in an Equation Will Show You the Way to the Solution)
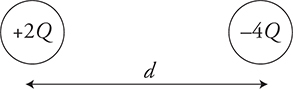
3. Two metal spheres with the same radius have charges of +2Q and −4Q. They are separated by a distance d, which is much larger than their radius, as shown in the figure. The two spheres exert a force F on each other. The spheres are brought into contact and again are placed a distance d apart. What is the new force between the spheres?
(A) 
(B) 
(C) 
(D) 
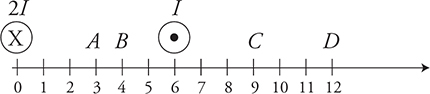
4. Two long wires carry current perpendicular to the page in opposite directions as shown in the figure. The left wire has twice the current of the right wire. At which location will the magnetic field be closest to zero?
(A) A
(B) B
(C) C
(D) D
Calculation Problems
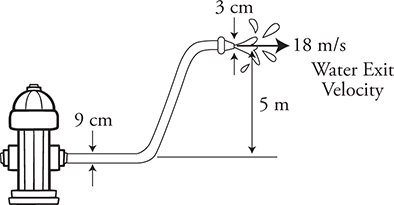
5. A firehose has a 3-cm diameter exit nozzle and a 9-cm diameter supply line from the hydrant that is 5 m below the nozzle as shown in the diagram. What pressure must be supplied at the hydrant to produce an exit velocity of 18 m/s? (Assume the density of water is 1000 kg/m3 and the exit pressure is 1 × 105 Pa.)
(A) 1.6 × 105 Pa
(B) 2.1 × 105 Pa
(C) 2.9 × 105 Pa
(D) 3.1 × 105 Pa
6. In an LED, electrons are made to drop across an electric potential and emit a photon of light. What must be the voltage drop to produce a blue light of 500 nm?
(A) 1 eV
(B) 1.5 eV
(C) 2 eV
(D) 2.5 eV
Ranking Tasks
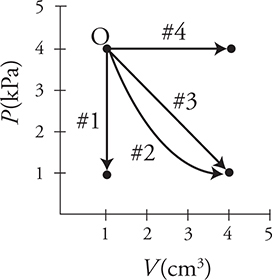
7. A gas beginning at point O on the graph can be taken along four paths to different ending conditions. Which of the following properly ranks the paths for change in temperature of the gas from most positive to most negative?
(A) ΔT4 > ΔT3 > ΔT2 > ΔT1
(B) ΔT4 > ΔT3 = ΔT2 > ΔT1
(C) ΔT4 = ΔT1 > ΔT3 = ΔT2
(D) ΔT3 = ΔT2 > ΔT4 = ΔT1
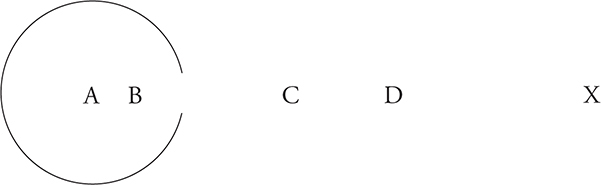
8. A large, hollow metal sphere with a small hole has a positive charge, as shown. A proton is released at rest from points A, B, C, and D. Assume that all protons, if they move, will move toward point X. Rank the velocity of the proton as it reaches point X from highest to lowest.
(A) A > B > C > D
(B) A = B > C > D
(C) D > C > B > A
(D) C > D > A = B
Experimental Description and Analysis
9. Students are asked to determine the number of molecules in a small, sealed pressurized cylinder of some unknown gas. There is a gauge on the cylinder that reads the internal pressure. What additional information and equipment will the students need to accomplish their task?
(A) a ruler and thermometer
(B) a ruler and type of gas inside the cylinder
(C) a thermometer, and type of gas inside the cylinder
(D) the type of gas in the cylinder and the average speed of the molecules
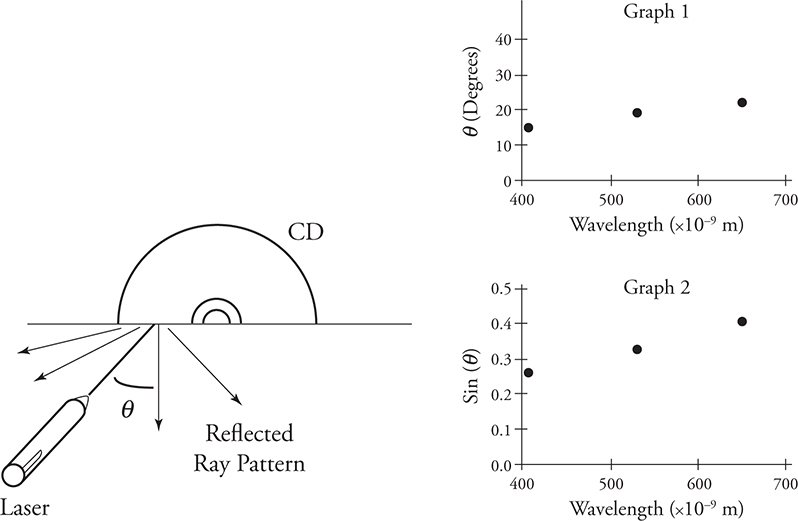
10. Students are attempting to calculate the narrow track spacing etched onto a CD. During the experiment, students shine a laser onto the surface of the CD to produce an interference pattern of reflected rays. The students measure the angle θ between the central ray and the first ray to the side as shown in the figure. This process is repeated for a red, green, and blue laser, and the data is presented in two graphs. Which of the following will be equal to the track spacing of the CD?
(A) the slope of the best-fit line for graph 1
(B) the slope of the best-fit line for graph 2
(C) the inverse of the slope of the best-fit line for graph 1
(D) the inverse of the slope of the best-fit line for graph 2
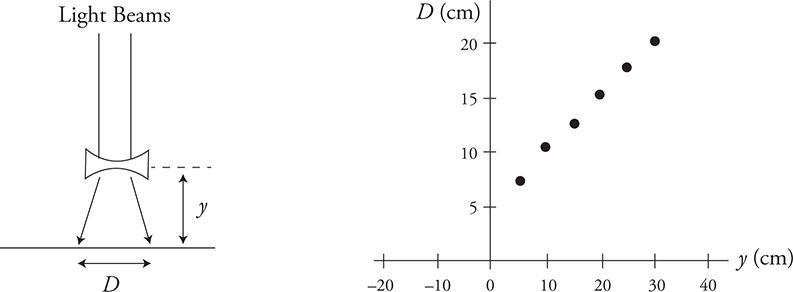
11. Two parallel light beams pass directly through a diverging lens producing two dots on a tabletop as shown in the figure. The spacing between the dots D is measured. This process is repeated for several distances y between the lens and the tabletop and the data is plotted. Using this information, determine the focal length of the lens.
(A) 0.5 cm
(B) 5.0 cm
(C) 10 cm
(D) −10 cm
Multiple Questions Referring to the Same Stem
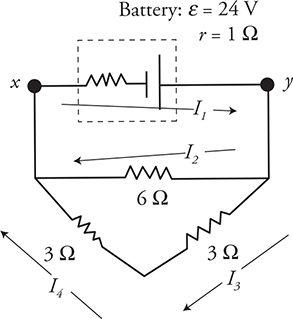
Questions 12—14 refer to the following material.
The circuit shown in the figure has a battery with an emf of 24 V and internal resistance of 1 Ω and three external resistors. The arrows show the currents I1, I2, I3, and I4 through each resistor.
12. What is the equivalent resistance of the three external resistors?
(A) 12 Ω
(B) 3.0 Ω
(C) 2.3 Ω
(D) 1.2 Ω
13. Which of the following correctly ranks the currents I1, I2, I3, and I4?
(A) I1 = I2 > I3 = I4
(B) I1 > I2 = I3 = I4
(C) I1 > I2 > I3 = I4
(D) I1 > I2 > I3 > I4
14. When operating as shown, what is the voltage difference VXY of the battery?
(A) ε
(B) ε − I1(1 Ω)
(C) ε + I1(1 Ω)
(D) I2(6 Ω) + I3(3 Ω) + I4(3 Ω)
Multiple-Correct Questions
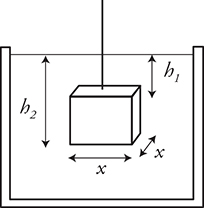
15. A mass m is suspended in a fluid of density ρ by a string as shown in the figure. The tension in the string is FT. Which of the following are correct mathematical statements? (Select two answers.)
(A) Fb = x2ρgh2
(B) Fb = x2ρg(h2 — h1)
(C) Fb = mg
(D) Fb = mg — FT
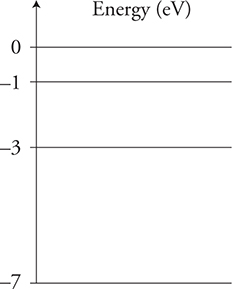
16. An energy-level diagram for an atom is shown in the diagram. Which of the following would be possible for this atom with an electron in the first excited state? (Select two answers.)
(A) absorption of an 8 eV photon
(B) absorption of a 1 eV photon
(C) emission of a 2 eV photon
(D) emission of a 4 eV photon
Experimental Design Free Response
17. In a laboratory experiment, your teacher has asked you to experimentally find the index of refraction of a clear rectangular block of glass. On the supply table are laser pointers (red, green, and blue) and other commonly available lab equipment.
(a) List the equipment you would choose to successfully carry out your investigation.
(b) Sketch the setup for your investigation. Indicate all the items you will be using. Clearly label and show the measurements you would take.
(c) Outline the experimental procedure you would use to gather the necessary data. Make sure the outline contains sufficient detail so that another student could follow your procedure.
(d) The table shows data taken by another group for a clear plastic block. Using this data, what quantities would you plot that would produce a straight line that could be used to determine the index of refraction of the plastic block?
(e) Using your answer from (d), plot the data and determine the index of refraction using a best-fit line.
(f) Your teacher tells you that your glass block has a larger index of refraction than the other group’s plastic block. Sketch what your data might look like on the graph from part (e).
Qualitative-Quantitative Transition Free Response
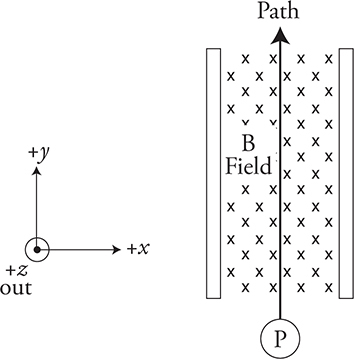
18. A proton traveling at a velocity v in the upward (+y) direction passes undeflected through a capacitor as shown. The capacitor plates are separated by a distance d = 0.05 m, have an area of A = 0.004 m2, and a constant potential difference of ΔV = 20,000 V. A uniform magnetic field B = 0.40 T directed into the page (−z direction) completely covers the area between the plates. Assume the effects of gravity are negligible compared to other forces.
(a) Which capacitor plate has the highest electric potential? Explain how you came to this conclusion.
(b) Derive an algebraic expression for the velocity of the proton so that it maintains an undeflected path through the capacitor plates. Use your expression to calculate a numerical value for the velocity.
(c) The proton is replaced with an electron with the same velocity and launched upward through the plates. Compare the motion of the electron with that of the proton. Justify your response using your answer to (b).
(d) The electron is now given twice the velocity of the proton and travels upward through the plates. On the figure, sketch the path of this electron. Justify your answer.
(e) Derive an algebraic expression for the acceleration of the double-speed electron. Use your expression to calculate a numerical value for the acceleration.
Paragraph-Length Argument Free Response
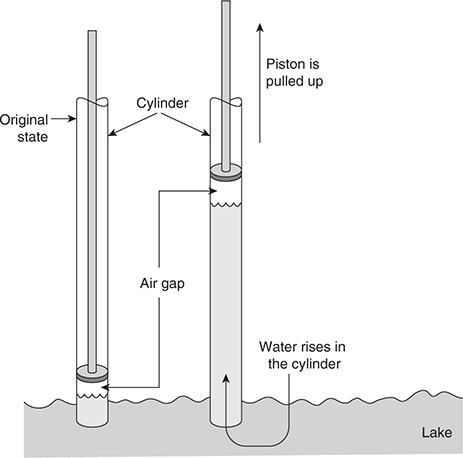
19. A very tall cylinder with a movable piston is placed in a lake. The piston is pulled up, drawing lake water in and upward, as shown in the figure. In a clear, coherent, paragraph-length response, explain why the lake water moves up the cylinder when the piston is pulled upward. In your explanation include what is happening to the air gap above the water in the piston.
Answers to AP Physics 2 Question-Types Assessment
1. D—Both samples have the same temperature and average molecular kinetic energy. Hydrogen is less massive and must move faster on average to have the same average kinetic energy. This means the peak will shift to the right. Since both samples have the same number of moles of gas, the area under the graph must be the same. This means the peak must also shift downward as it shifts to the right.
2. B—At location B the two charges on the left create an electric field directed to the right that is much larger than the leftward-directed electric fields created by the two other positive charges, because they are farther away.
3. A—When the spheres touch, they share the combined charge by conduction. This leaves a net charge of —2Q that will be equally distributed on each sphere. Thus, each sphere ends up with a final charge of —Q. This means that the left charge has decreased by a factor of 2 and the right charge has decreased by a factor of 4. Using Coulomb’s law, we get a final force of one-eighth the original:
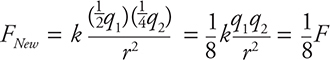
4. D—Using the right-hand rule for magnetic fields around current carrying wires, we determine that the magnetic field rotates clockwise around the left wire and counterclockwise around the right wire. Thus, choices A and B cannot be correct, as the two B-fields add in the downward direction. Thus, the choice is between C and D.
Using the equation: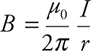 
we see that the left wire, with twice the current, must also have twice the radius in order to produce the same size B-field as the right wire: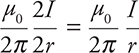 
Point D satisfies this condition.
5. D—Using the conservation of mass/continuity equation, we see that the water at the hydrant must be going slower than at the nozzle: A1v1 = A2v2.
The area of the hose is proportional to the diameter squared: πr12v1 = πr22v2. This gives a velocity at the hose of 2 m/s.
Using conservation of energy/Bernoulli’s equation:
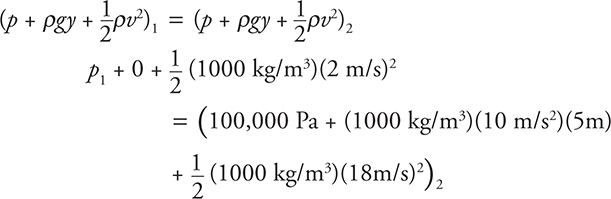
Plugging in the values, we get a required pressure of 3.1 × 105 Pa at the hydrant.
6. D—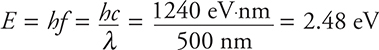
7. B—Temperature is directly related to the PV value. The starting position has a PV value of 4PV. Path 4 takes the gas to a PV value of 16PV, so ΔT is positive. Paths 2 and 3 take the gas to a PV, value of 4PV so ΔT is zero. Path 1 takes the gas to a lower final PV value so ΔT is negative.
8. D—Inside a charged conductor, the electric field is zero and the electric potential is constant. Thus, the charges inside the sphere do not experience a force and will not move at all. Outside of the sphere, the positive charges are repelled to the right. The electric potential decreases as the charges move away from the sphere. Since charge C will experience the largest change in potential, it will gain more kinetic energy than D.
9. A—With a ruler, the volume of the cylinder can be calculated. Knowing the volume, temperature, and pressure, the number of moles and number of molecules of gas can be calculated using the ideal gas law.
10. D—The independent variable is wavelength and the dependent variable is angle. Solving the interference pattern equation (d sin θ = mλ) for the independent variable, we get: 
, where m equals 1 because the students measure the angle to the first order maxima. Thus, to find the track spacing, we need to find the slope of graph 2 and take the inverse of it.
11. D—Extrapolating the data to where the parallel light beams would cross, we get a focal length of −10 cm.
12. B—The two 3 Ω resistors are in series giving 6 Ω, which adds in parallel with the 6 Ω resistor to give a total resistance of 3 Ω.
13. B—I1 is in the main line and must be the largest. I1 splits into I2 and I3, which must be the same because the resistance in each line is 6 Ω. I3 = I4. They are the same because there are no branching lines.
14. B—Between points X and Y the battery contributes +ε = +24 V while the internal resistance consumes —ΔV = —Ir = —I1 (1 Ω).
15. B and D—Fb = ρVg = x2ρg(h2 — h1) where x2(h2 — h1) is the volume of the mass. Since the mass is stationary, the forces on it must cancel out: Fb + FT = mg.
16. A and D—From the first excited state, the electron could absorb the 8 eV photon, which will ionize the atom sending the electron away with 5 eV of kinetic energy. The atom could also emit a 4 eV photon, which would send the electron down to the −7 eV energy level.
17. (a) Start with the equation that models refractive behavior, Snell’s law: ni sin θi = nr sin θr. You will need a way to measure angles. This could be accomplished with a protractor, or just a ruler if you choose to use trig functions to calculate the angle. You will also need a light source (one of the lasers) and a method for tracing the angles, like a piece of paper, pencil, and ruler.
(b) See sketch.
(c) Place the glass block on a piece of paper and trace the outline. Shine a laser into the block and trace its path. Mark the exit location of the beam on the other side of the block. Remove the block from paper and use exit marks to trace the ray’s path inside the glass. Draw the normal line at the entry point of the ray into the glass, and then measure the angles of incidence and refraction as shown in the picture. Repeat for multiple angles.
(d) This is called linearizing the graph. Plot sin θr as a function of sin θi to create a straight line. The slope will equal 1/nr. (You could also swap the axis, but I plotted the independent variable on the x-axis and the dependent variable on the y-axis. As you should!) We will discuss more about linearization in Chapter 6.
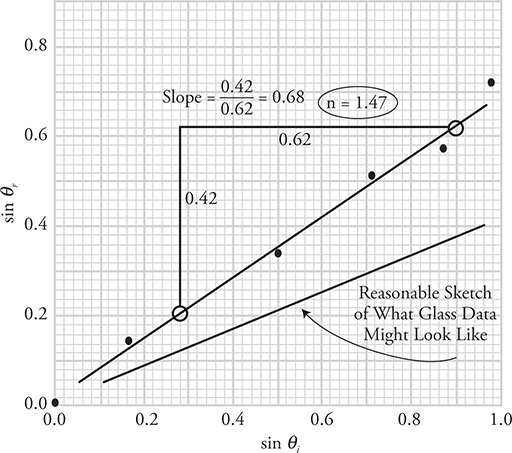
(e) Notice how the best fit line represents the average of the data and does not even go through any of the data points! Do not use the data points to calculate the slope. Pick two convenient points from the best-fit line as shown in the figure. The slope is 0.68 = 1/nr. Invert and get nr = 1.47.
(f) Since the slope of the graph is the inverse of the index of refraction, and the glass block has a larger index of refraction, the graph for the glass block should have a shallower slope and still pass through zero. (See the graph.)
18. (a) The left plate. Using the right-hand rule for magnetic forces on moving charges, we see that the magnetic force will be directed to the left. Therefore, we need an electric force to the right. Since the proton is positively charged, we need an electric field to the right to accomplish this, and thus, the left plate must be positive and the right plate negative.
(b) For a charged particle to pass undeflected straight through crossed perpendicular magnetic and electric fields, the electric and magnetic forces on the charge must cancel.
Note that since the velocity is perpendicular to the magnetic field: sin θ = sin (90°) = 1. Therefore, E = vB when the charge travels in a straight line through the fields.
(c) The electron also passes through the plates undeflected. The charge canceled out of the equation derived in (b) 
.
(d) The electron will curve to the right between the plates. The magnitude of the electric force does not change. However, the increased velocity of the electron causes the magnetic force to become larger. Using the right-hand rule for forces on moving charges, we can see that the increased magnet force causes the electron to accelerate to the right.
(e) 
19. As the piston is pulled upward, the volume of the air gap increases. This decreases the pressure in the air gap as shown by the ideal gas law: PV = nRT. This causes a decrease in the water pressure at the bottom of the cylinder as shown by the static pressure equation: P = P0 + ρgh. The atmospheric pressure on top of the lake is still the same. Therefore, there is a greater pressure in the lake water than in the water at the bottom of the cylinder. Therefore, water is pushed up the cylinder until the pressure at the bottom of the cylinder is in equilibrium with the water pressure of the lake. Note that water is NOT sucked up the tube.