AP Physics C Exam
Part IV
Content Review for the AP Physics C Exam
3 Vectors
4 Kinematics
5 Newton’s Laws
6 Work, Energy, and Power
7 Linear Momentum
8 Rotational Motion
9 Laws of Gravitation
10 Oscillations
11 Electric Forces and Fields
12 Electric Potential and Capacitance
13 Direct Current Circuits
14 Magnetic Forces and Fields
15 Electromagnetic Induction
16 Solutions to the Chapter Review Questions
Chapter 3
Vectors
INTRODUCTION
Vectors will show up all over the place in our study of physics. Some physical quantities that are represented as vectors are: displacement, velocity, acceleration, force, momentum, and electric and magnetic fields. Since vectors play such a recurring role, it’s important to become comfortable working with them; the purpose of this chapter is to provide you with a mastery of the fundamental vector algebra we’ll use in subsequent chapters. For now, we’ll restrict our study to two-dimensional vectors (that is, ones that lie flat in a plane).
DEFINITION
A vector is a quantity that involves both magnitude and direction and obeys the commutative law for addition, which we’ll explain in a moment. A quantity that does not involve direction is a scalar. For example, the quantity 55 miles per hour is a scalar, while the quantity 55 miles per hour to the north is a vector. Other examples of scalars include: mass, work, energy, power, temperature, and electric charge.
Vectors can be denoted in several ways, including:
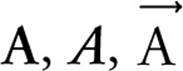
In textbooks, you’ll usually see one of the first two, but when it’s handwritten, you’ll see the last one.
Displacement (which is the difference between the final and initial positions) is the prototypical example of a vector:
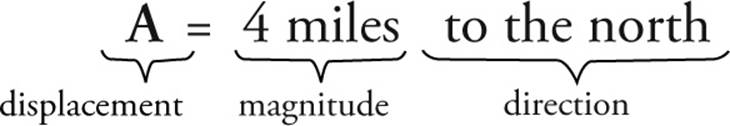
When we say that vectors obey the commutative law for addition, we mean that if we have two vectors of the same type, for example another displacement,
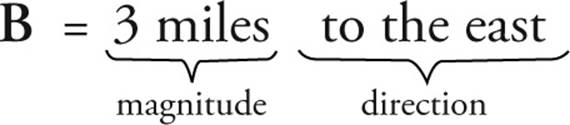
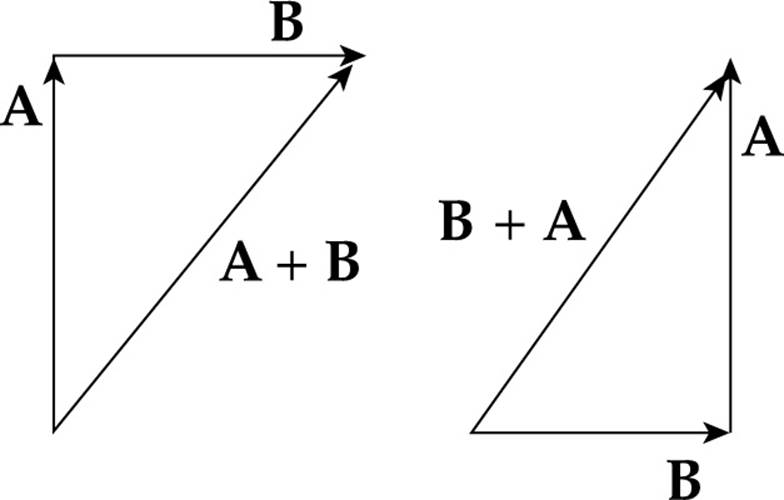
then A + B must equal B + A. The vector sum A + B means the vector A followed by B, while the vector sum B + A means the vector B followed by A. That these two sums are indeed identical is shown in the following figure:
Two vectors are equal
if they have the same
magnitude and the same
direction.
VECTOR ADDITION (GEOMETRIC)
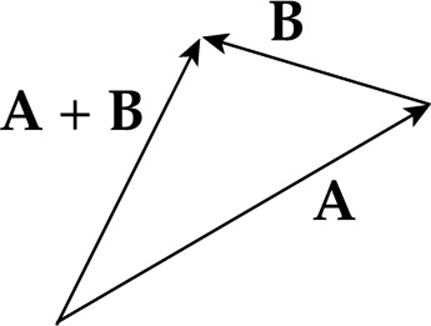
The figure above illustrates how vectors are added to each other geometrically. Place the tail (the initial point) of one vector at the tip of the other vector, then connect the exposed tail to the exposed tip. The vector formed is the sum of the first two. This is called the “tip-to-tail” method of vector addition.
Example 1 Add A + B using the two following vectors:

Solution. Place the tail of B at the tip of A and connect them:
SCALAR MULTIPLICATION
A vector can be multiplied by a scalar (that is, by a number), and the result is a vector. If the original vector is A and the scalar is k, then the scalar multiple kA is as follows:
magnitude of kA = |k| × (magnitude of A)
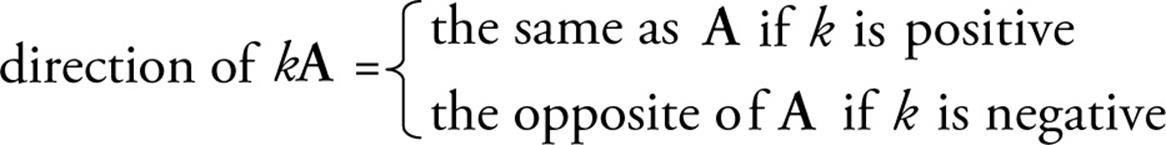
Example 2 Sketch the scalar multiples 2A, ![]() A, –A, and –3A of the vector A:
A, –A, and –3A of the vector A:

Solution.

Keep in mind that when you multiply a vector times a scalar of k, the vector becomes k times longer.
VECTOR SUBTRACTION (GEOMETRIC)
To subtract one vector from another, for example, to get A – B, simply form the vector –B, which is the scalar multiple (–1)B, and add it to A:
A – B = A + (–B)
Example 3 For the two vectors A and B, find the vector A – B.
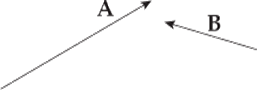
Solution. Flip B around—thereby forming –B—and add that vector to A:
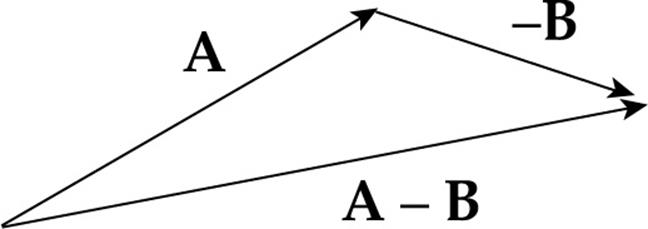
It is important to know that vector subtraction is not commutative: you must perform the subtraction in the order stated in the problem.
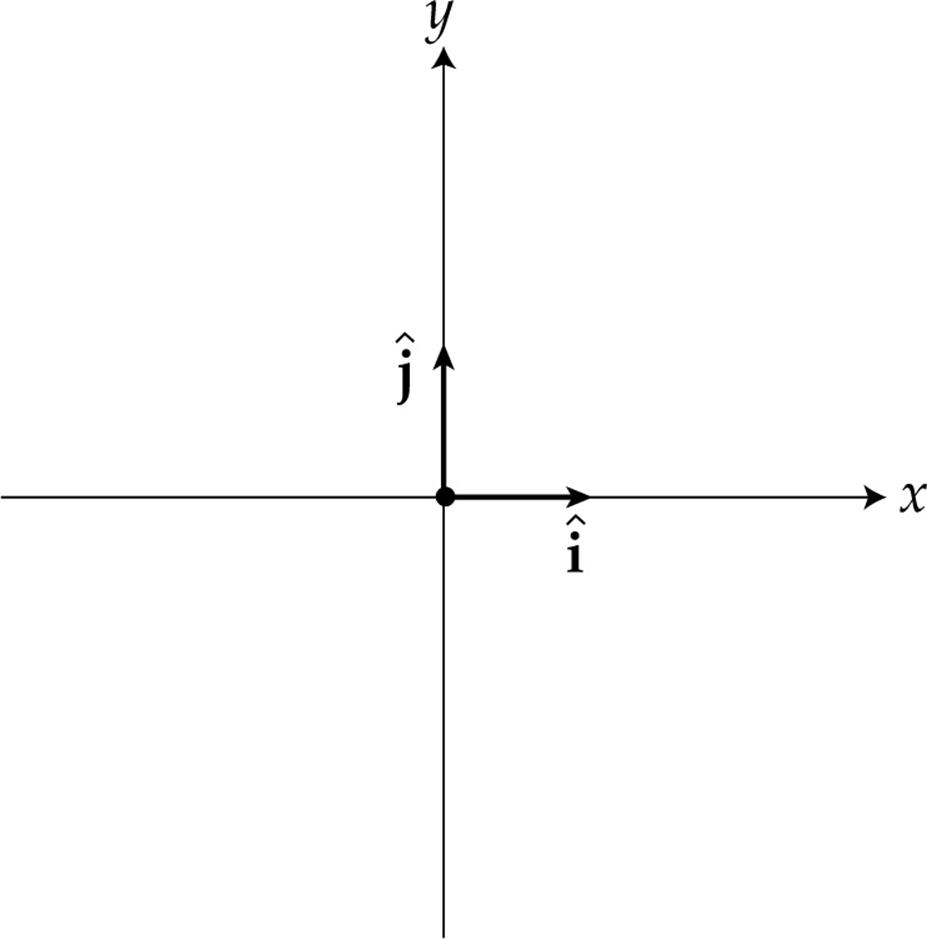
STANDARD BASIS VECTORS
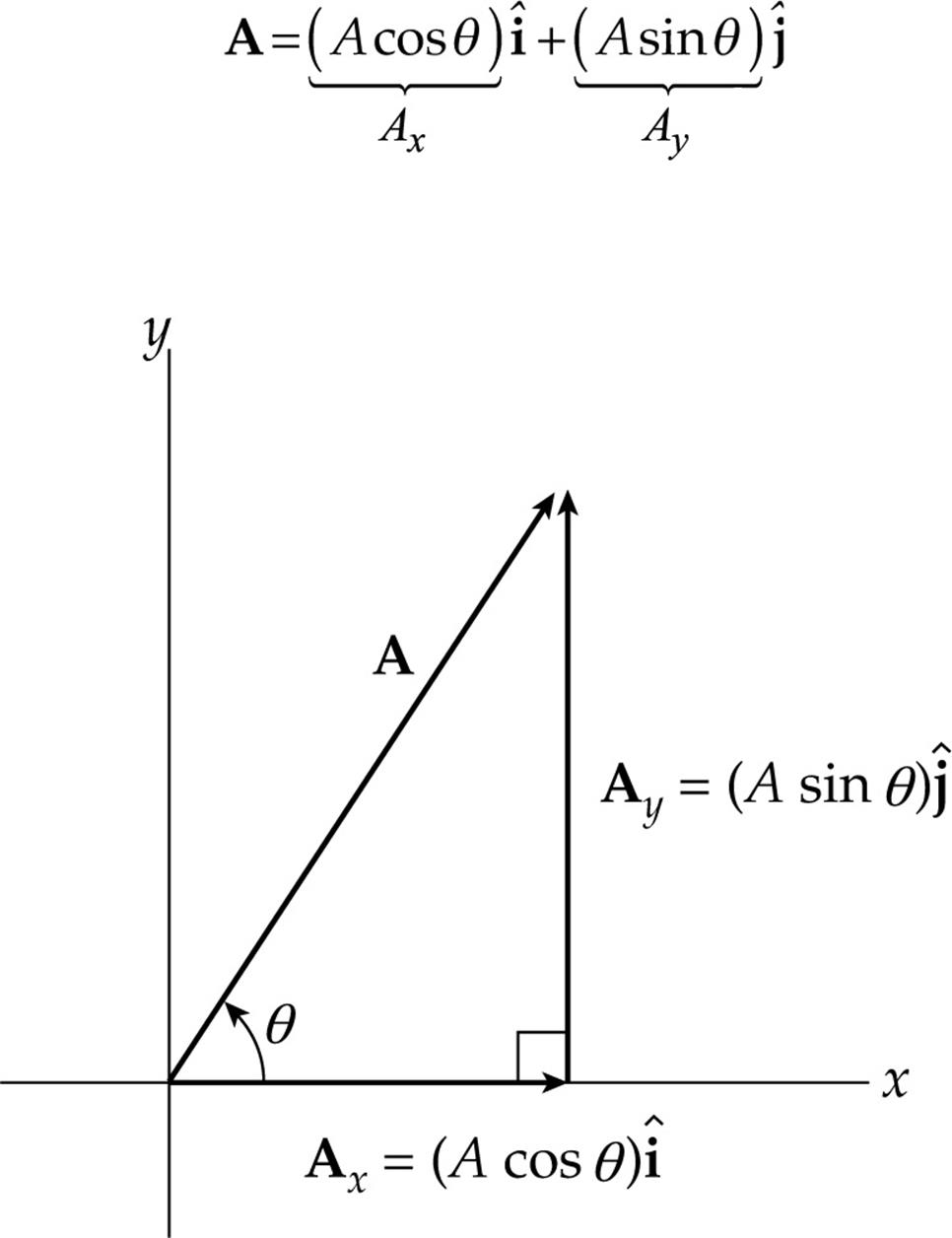
Two-dimensional vectors, that is, vectors that lie flat in a plane, can be written as the sum of a horizontal vector and a vertical vector. For example, in the following diagram, the vector A is equal to the horizontal vector B plus the vertical vector C:

The horizontal vector is always considered a scalar multiple of what’s called the horizontal basis vector, i, and the vertical vector is a scalar multiple of the vertical basis vector, j. Both of these special vectors have a magnitude of 1, and for this reason, they’re called unit vectors. Unit vectors are often represented by placing a hat (caret) over the vector; for example, the unit vectors i and j are sometimes denoted ![]() and
and ![]() , or
, or ![]() and
and ![]() .
.
For instance, the vector A in the figure below is the sum of the horizontal vector B = 3![]() and the vertical vector C = 4
and the vertical vector C = 4![]() .
.
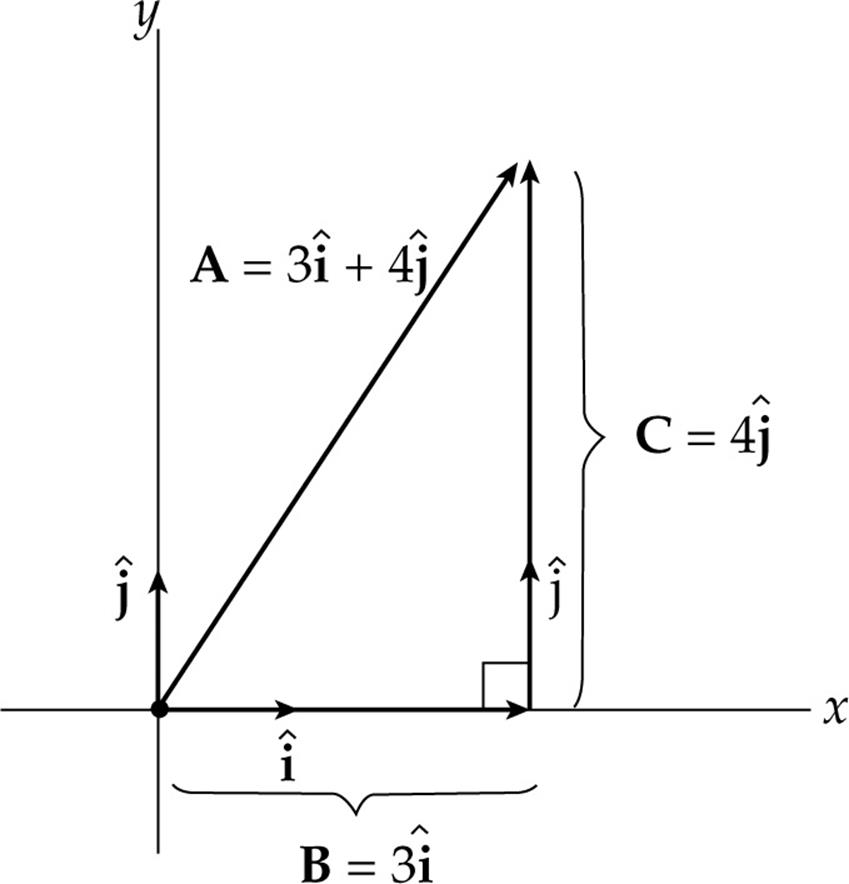
The vectors B and C are called the vector components of A, and the scalar multiples of ![]() and
and ![]() which give A—in this case, 3 and 4—are called the scalar components of A. So vector A can be written as the sum Ax
which give A—in this case, 3 and 4—are called the scalar components of A. So vector A can be written as the sum Ax![]() + Ay
+ Ay![]() , where Ax and Ay are the scalar components of A. The componentAx is called the horizontal scalar component of A, and Ay is called the vertical scalar component of A.
, where Ax and Ay are the scalar components of A. The componentAx is called the horizontal scalar component of A, and Ay is called the vertical scalar component of A.
VECTOR OPERATIONS USING COMPONENTS
The use of components makes the vector operations of addition, subtraction, and scalar multiplication pretty straightforward.
Vector addition: Add the respective components
A + B = (Ax + Bx)![]() + (Ay + By)
+ (Ay + By)![]()
Vector subtraction: Subtract the respective components
A – B = (Ax – Bx)![]() + (Ay – By)
+ (Ay – By)![]()
Scalar multiplication: Multiply each component by k
kA = (kAx)![]() + (kAy)
+ (kAy)![]()
Example 4 If A = 2![]() – 3
– 3![]() and B = –4
and B = –4![]() + 2
+ 2![]() , compute each of the following vectors: A + B, A – B, 2A, and A + 3B.
, compute each of the following vectors: A + B, A – B, 2A, and A + 3B.
Solution. It’s very helpful that the given vectors A and B are written explicitly in terms of the standard basis vectors ![]() and
and ![]() :
:
A + B = (2 – 4)![]() + (–3 + 2)
+ (–3 + 2)![]() = –2
= –2![]() –
– ![]()
A – B = [2 – (–4)]![]() + (–3 –2)
+ (–3 –2)![]() = 6
= 6![]() – 5
– 5![]()
2A= 2(2)![]() + 2(–3)
+ 2(–3)![]() = 4
= 4![]() – 6
– 6![]()
A + 3B = [2 + 3(–4)]![]() + [–3 + 3(2)]
+ [–3 + 3(2)]![]() = –10
= –10![]() + 3
+ 3![]()
MAGNITUDE OF A VECTOR
The magnitude of a vector can be computed with the Pythagorean theorem. The magnitude of vector A can be denoted in several ways: A or |A| or ||A||. In terms of its components, the magnitude of A = Ax![]() + Ay
+ Ay![]() is given by the equation
is given by the equation
A = 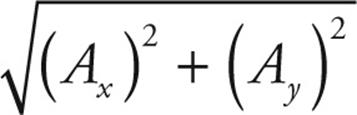
which is the formula for the length of the hypotenuse of a right triangle with sides of lengths Ax and Ay.
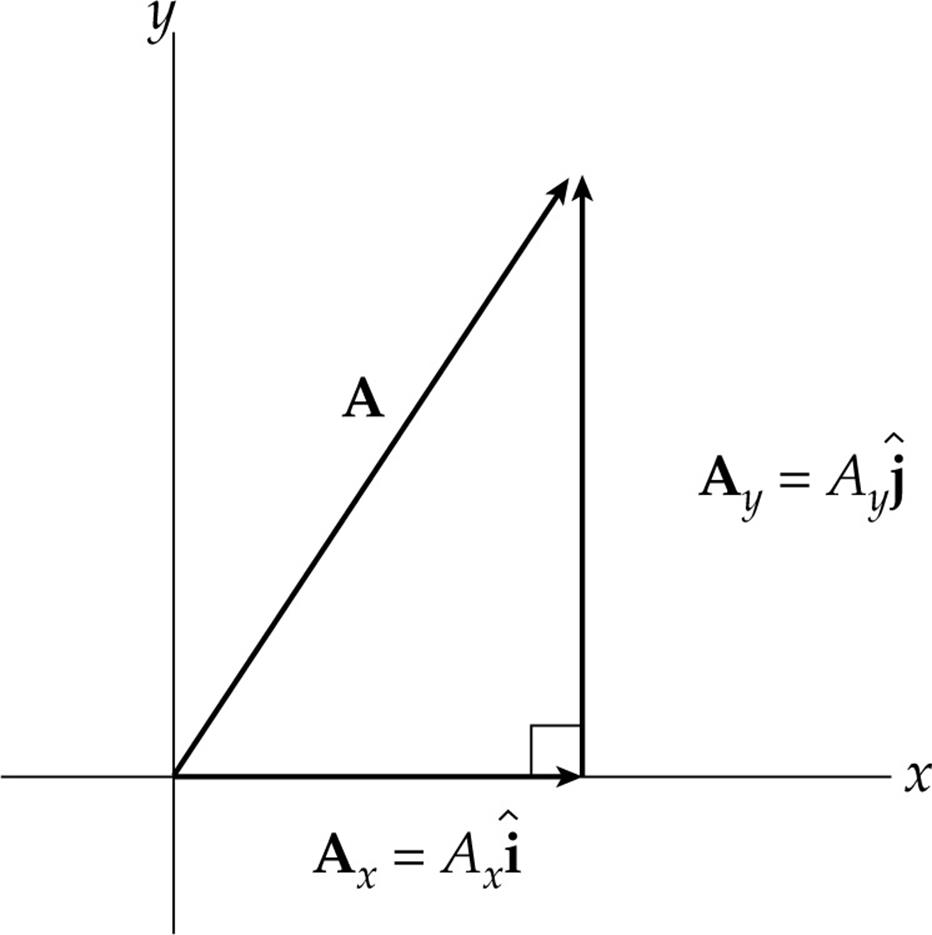
DIRECTION OF A VECTOR
The direction of a vector can be specified by the angle it makes with the positive x-axis. You can sketch the vector and use its components (and an inverse trig function) to determine the angle. For example, θ if denotes the angle that the vector A = 3![]() + 4
+ 4![]() makes with the +x axis, then tanθ = 4/3, so θ = tan–1(4/3) = 53.1°. Make sure your calculator is in the correct mode, either radian or degree, when using trig functions.
makes with the +x axis, then tanθ = 4/3, so θ = tan–1(4/3) = 53.1°. Make sure your calculator is in the correct mode, either radian or degree, when using trig functions.

If A makes the angle θ with the +x axis, then its x- and y-components are A cos θ and A sin θ, respectively (where A is the magnitude of A).
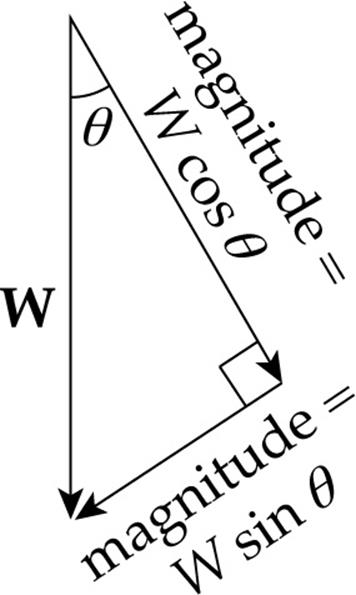
In general, any vector in the plane can be written in terms of two perpendicular component vectors. For example, vector W (shown below) is the sum of two component vectors whose magnitudes are W cos θ and W sin θ:
THE DOT PRODUCT
A vector can be multiplied by a scalar to yield another vector, as you saw in Example 2. For instance, we can multiply the vector A by the scalar 2 to get the scalar multiple 2A. The product is a vector that has twice the magnitude and, since the scalar is positive, the same direction as A.
Additionally, we can form a scalar by multiplying two vectors. The product of the vectors in this case is called the dot product or the scalar product, since the result is a scalar. Several physical concepts (work, electric and magnetic flux) require that we multiply the magnitude of one vector by the magnitude of the component of the other vector that’s parallel to the first. The dot product was invented specifically for this purpose.
Consider these two vectors, A and B:
In order to find the component of B that’s parallel to A, we do the following:
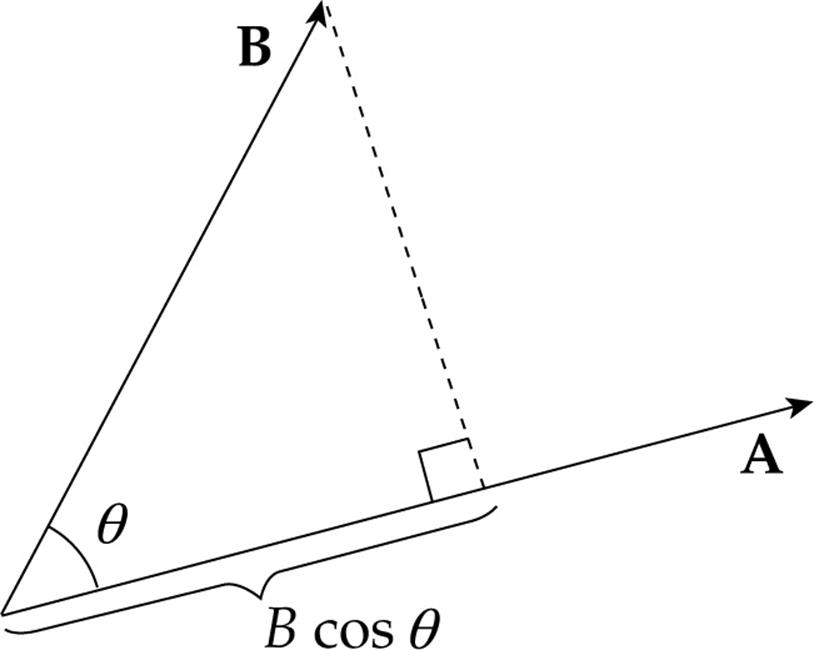
As this figure shows, the component of B that’s parallel to A has the magnitude B cos θ. So if we multiply the magnitude of A by the magnitude of the component of B that’s parallel to A, we would form the product A(B cos θ). This is the definition of the dot product of the vectors A andB
A • B = AB cos θ
where θ is the angle between A and B. Notice that the dot product of two vectors is a scalar.
The angle between the vectors is crucial to the value of the dot product. If θ = 0, then the vectors are already parallel to each other, so we can simply multiply their magnitudes: A • B = AB. If A and B are perpendicular, then there is no component of B that’s parallel to A (or vice versa), so the dot product should be zero. And if θ is greater than 90°,
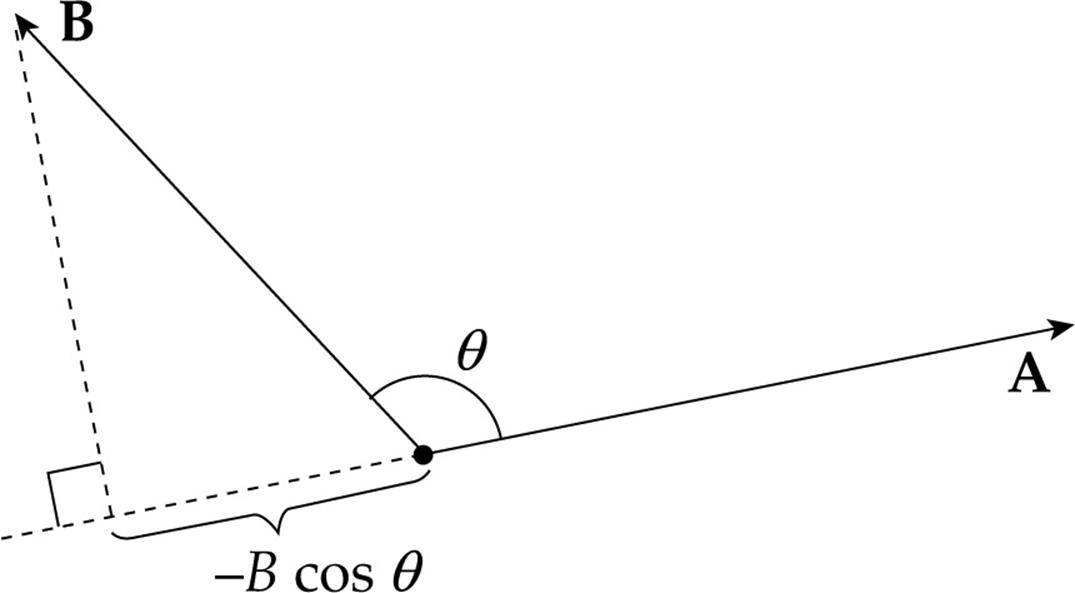
then the component of one that’s parallel to the other is actually antiparallel (backwards), and this will give the dot product a negative value (because cos θ < 0 if 90° < θ < 180°).
The value of the dot product can, of course, be figured out using the definition above (AB cos θ) if θ is known. If θ is not known, the dot product can be calculated from the components of A and B in this way:
A • B =(Ax![]() + Ay
+ Ay![]() ) • (Bx
) • (Bx![]() + By
+ By![]() ) = AxBx + AyBy
) = AxBx + AyBy
This means that, to form the dot product, simply add the product of the scalar x components and the product of the scalar y components.
Example 5
(a) What is the dot product of the unit vectors ![]() and
and ![]() ?
?
(b) What is the product of the unit vectors ![]() and
and ![]() ?
?
Solution.
(a) Since ![]() and
and ![]() are perpendicular to each other (θ = 90°), their dot product must be zero, because cos 90° = 0. (In fact, unless A or B already has magnitude zero, it’s also true that two vectors are perpendicular to each other when their dot product is zero.)
are perpendicular to each other (θ = 90°), their dot product must be zero, because cos 90° = 0. (In fact, unless A or B already has magnitude zero, it’s also true that two vectors are perpendicular to each other when their dot product is zero.)
(b) Because ![]() and
and ![]() are parallel to each other, their dot product is just the product of the magnitudes, which is 1 • 1 = 1.
are parallel to each other, their dot product is just the product of the magnitudes, which is 1 • 1 = 1.
Example 6 If A= –2![]() + 4
+ 4![]() and B= 6
and B= 6![]() + By
+ By![]() , find the value of By such that the vectors A and B will be perpendicular to each other.
, find the value of By such that the vectors A and B will be perpendicular to each other.
Solution. Two vectors are perpendicular to each other if their dot product is zero. The dot product of A and B can be determined as follows: Multiply the scalar x components, (–2)(6) = –12, multiply the scalar y components, (4)(By), and add them: –12 + 4By. Setting this equal to 0, we see that By must equal 3.
THE CROSS PRODUCT
Some physical concepts (torque, angular momentum, magnetic force) require that we multiply the magnitude of one vector by the magnitude of the component of the other vector that’s perpendicular to the first. The cross product was invented for this specific purpose.
Consider these two vectors A and B:
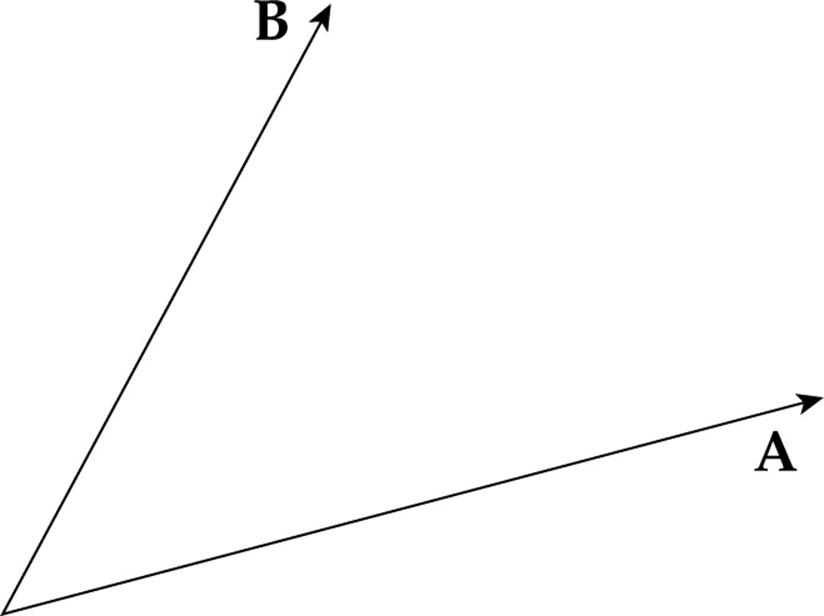
In order to find the component of one of these vectors that’s perpendicular to the other one, we do the following:
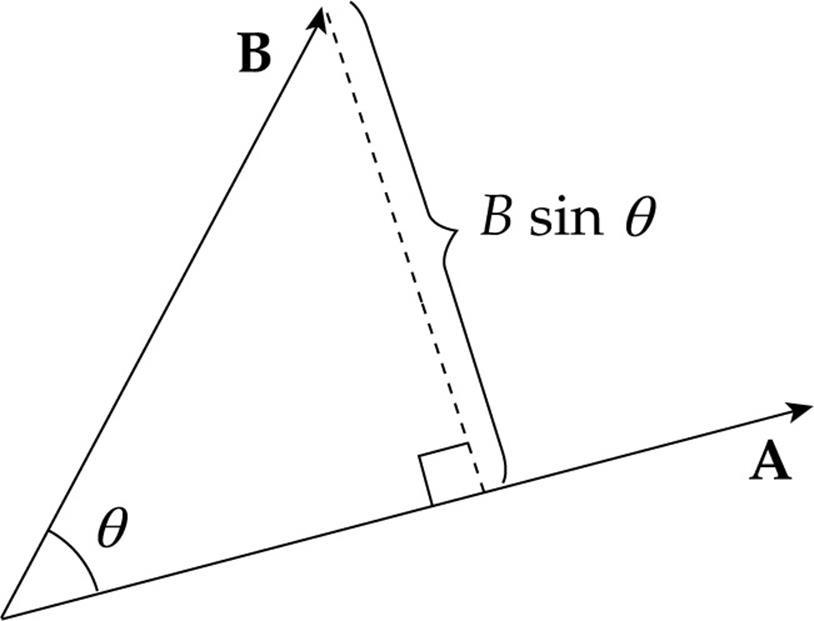
As this figure shows, the component of B that’s perpendicular to A has magnitude B sin θ. Therefore, if we multiply the magnitude of A by the magnitude of the component of B that’s perpendicular to A, we form the product A(B sin θ). This is the magnitude of what’s called the cross product of the vectors A and B, denoted A × B:
|A × B| = AB sin θ
where θ is the angle between A and B (such that 0° ≤ θ ≤ 180°).
The equation above gives the magnitude of the cross product. The cross product of two vectors is another vector that’s always perpendicular to both A and B, with its direction determined by a procedure known as the right-hand rule. The direction of A × B is perpendicular to the plane that contains A and B, but this leads to an ambiguity, since there are two directions perpendicular to a plane (one on either side; they point in opposite directions). The following description resolves this ambiguity.
Make sure you are using your right hand. Point your index finger in the direction of the first vector, A, then point your middle finger in the direction of the second vector, B, and your thumb now points in the direction of the cross product, A × B.
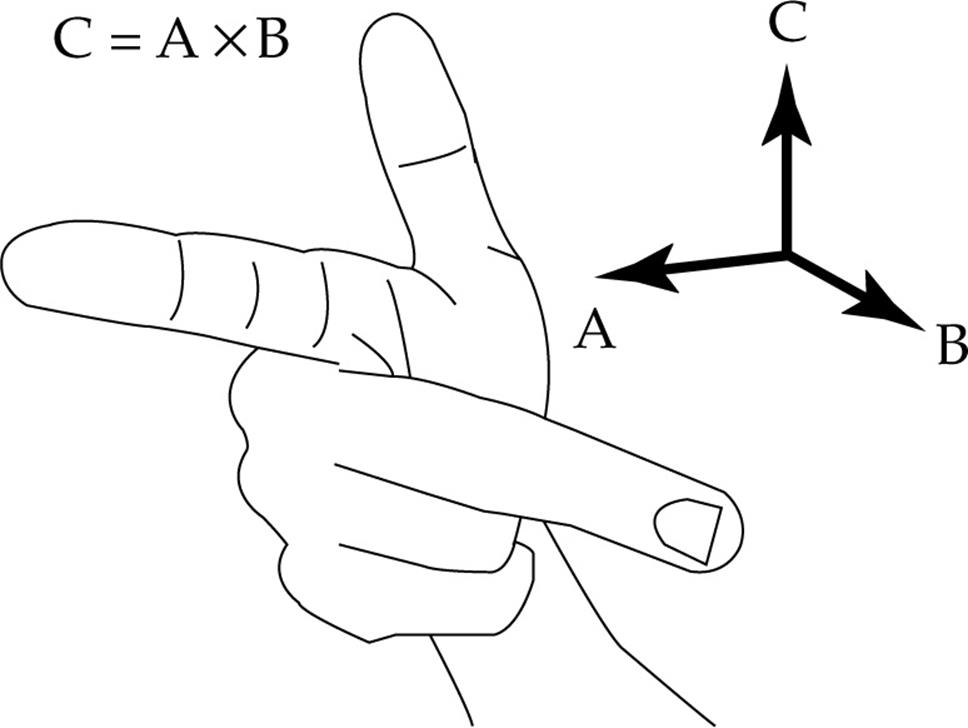
This is called the right-hand rule.
You know that the standard basis vectors ![]() and
and ![]() can be used to write any two-dimensional vector, but now that we have introduced the cross product we need a third basis unit vector to write three-dimensional vectors. This third unit vector is denoted
can be used to write any two-dimensional vector, but now that we have introduced the cross product we need a third basis unit vector to write three-dimensional vectors. This third unit vector is denoted ![]() and, like
and, like ![]() and
and ![]() , it points along the direction of a coordinate axis. The vector
, it points along the direction of a coordinate axis. The vector ![]() is the unit vector that points along the x-axis,
is the unit vector that points along the x-axis, ![]() along the y, and now
along the y, and now ![]() along the z. The three basis vectors are mutually perpendicular:
along the z. The three basis vectors are mutually perpendicular:
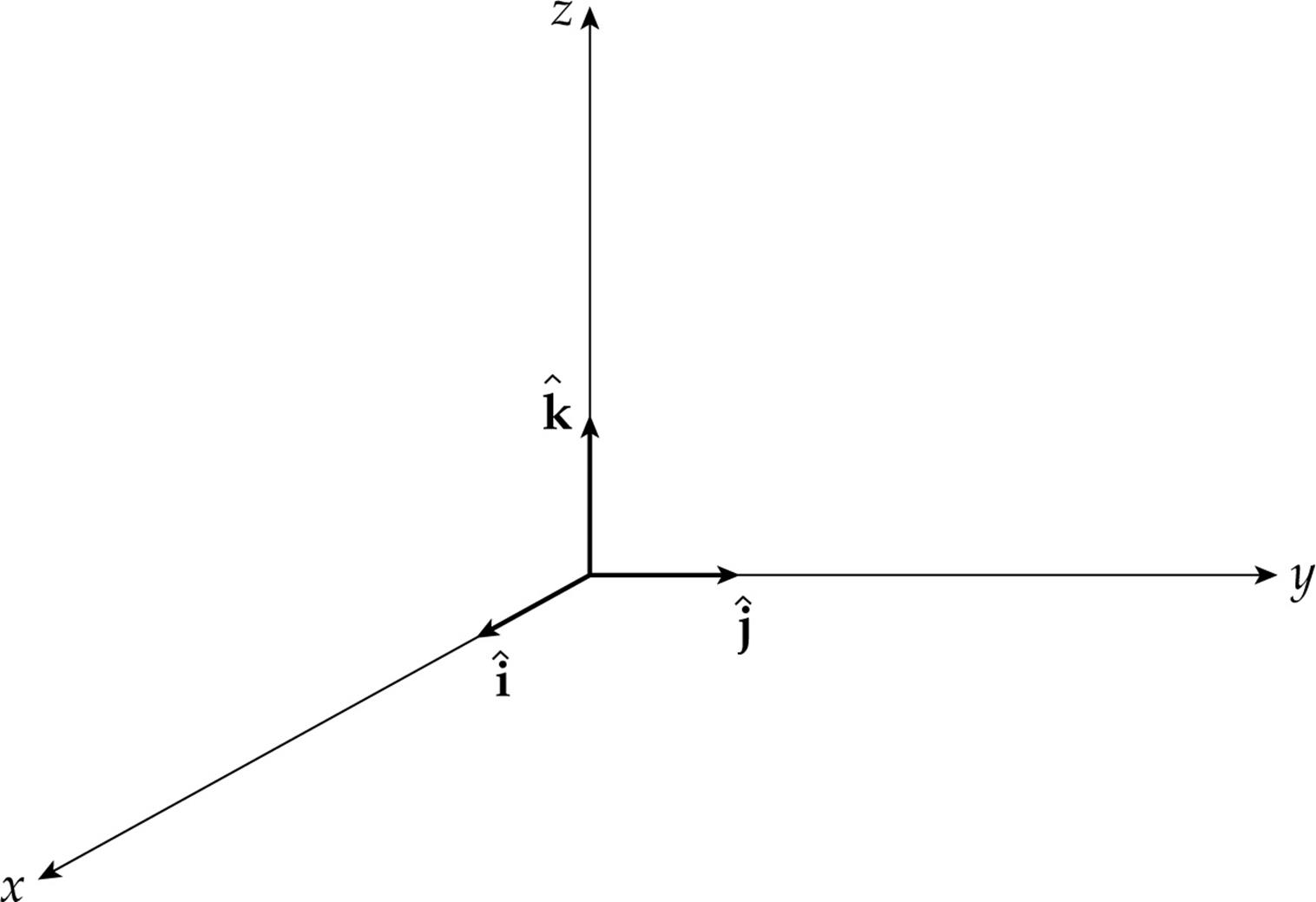
The coordinate axes shown define a right-handed coordinate system, because the directions of the x, y, and z axes obey the right-hand rule. That is, ![]() ×
× ![]() points in the direction of
points in the direction of ![]() . In fact,
. In fact, ![]() ×
× ![]() actually equals
actually equals ![]() , since the magnitude of
, since the magnitude of ![]() ×
× ![]() is 1. As a right-handed coordinate system,
is 1. As a right-handed coordinate system, ![]() ×
×![]() =
= ![]() and
and ![]() ×
× ![]() =
= ![]() .
.
Unlike the dot product, the cross product is not commutative; A × B is not equal to B × A. This is because applying the right-hand rule to determine the direction of B × A would give a vector that points in the direction opposite to that of A × B. Therefore, B × A = –(A × B).
The cross product can be computed directly from the scalar components of A and B without first determining the angle θ, as follows: If A = Ax![]() + Ay
+ Ay![]() + Az
+ Az![]() and B = Bx
and B = Bx![]() + By
+ By![]() + Bz
+ Bz![]() , then the cross product (magnitude and direction) of A and B is
, then the cross product (magnitude and direction) of A and B is
A × B = (AyBz – AzBy)![]() + (AzBx – AxBz)
+ (AzBx – AxBz)![]() + (AxBy – AyBx)
+ (AxBy – AyBx)![]()
This formula requires a lot of memorization. Another method for determining the cross product is to realize that the cross product is the determinant of the following 3 × 3 matrix.
A×B = 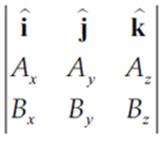 =
= 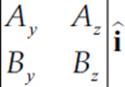 −
− 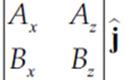 +
+ 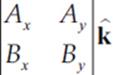
By taking the determinant of each 2 × 2 matrix you will realize that you get the same formula as shown above. This may appear to be equally difficult to memorize; however, you can just memorize two facts. Each 2 × 2 matrix is missing the column associated with the basis vector that multiplies it and the terms alternate in sign.
Example 7 Calculate the cross product of the vectors A = 2![]() + 3
+ 3![]() and B = –
and B = – ![]() +
+ ![]() + 4
+ 4![]() , and verify that it’s perpendicular to both A and B.
, and verify that it’s perpendicular to both A and B.
Solution. First we figure out the cross product:
A × B = [(3)(4) – (0)(1)]![]() – [(2)(4) – (0)(–1)]
– [(2)(4) – (0)(–1)]![]() + [(2)(1)– (3(–1)]
+ [(2)(1)– (3(–1)]![]() = 12
= 12![]() – 8
– 8![]() + 5
+ 5![]()
Using the determinant method
A×B = 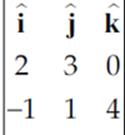 =
= 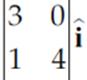 −
− 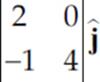 +
+ 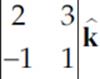
A×B = [(3)(4)−(0)(1)]![]() −[(2)(4)−(0)(1)]
−[(2)(4)−(0)(1)]![]() +[(2)(1)−(3)(−1)]
+[(2)(1)−(3)(−1)]![]()
A×B = 12![]() −8
−8![]() +5
+5![]()
Now, to verify that this vector is perpendicular to both A and B, we use the property of the dot product: Two vectors are perpendicular to each other if their dot product is zero. Extending the computation of the dot product in terms of the scalar components to three dimensions, we get:
(A × B) · A= (12![]() – 8
– 8![]() + 5
+ 5![]() ) · (2
) · (2![]() + 3
+ 3![]() ) = (12)(2) + (–8)(3) + (5)(0) = 0
) = (12)(2) + (–8)(3) + (5)(0) = 0
(A × B) · B= (12![]() – 8
– 8![]() + 5
+ 5![]() ) · (–
) · (– ![]() +
+ ![]() + 4
+ 4![]() ) = (12)(–1) + (–8)(1) + (5)(4) = 0
) = (12)(–1) + (–8)(1) + (5)(4) = 0