AP Physics B Exam
13 Magnetic Forces and Fields
INTRODUCTION
In Chapter 10, we learned that electric charges are the sources of electric fields and that other charges experience an electric force in those fields. The charges generating the field were assumed to be at rest, because if they weren”t, then another force field would have been generated in addition to the electric field. Electric charges that move are the sources of magnetic fields, and other charges that move can experience a magnetic force in these fields.
MAGNETIC FIELDS
Similar to our discussion about electric fields, the space surrounding a magnet is permeated by a magnetic field. The direction of the magnetic field is defined as pointing out of the north end of a magnet and into the south end of a magnet as illustrated below.
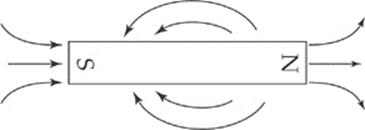
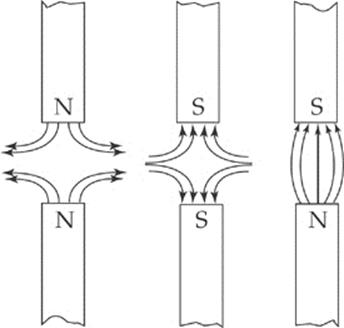
When two magnets get near each other the magnetic fields interfere with each other and can be drawn as follows. Note that, for simplicity”s sake, only the field lines closest to the poles are shown.
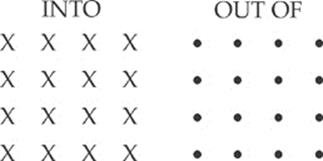
Notice there is a curve to the above fields. We call the field uniform if the field lines are parallel and of equal strength. It is easy to recognize a uniform magnetic field to the right, left, top of the page, or bottom of the page. But you will also see a field going into or out of the page. A field into the page looks as if there were a north pole of a magnet above the page pointing down at the south pole of a magnet that is below the page. It is represented by an area with X”s going into the page. A field coming out of the page looks as if there were a north pole of a magnet below the page pointing up at the south pole of a magnet that is above the page. It is represented by an area with dots (•) coming out of the page.
THE MAGNETIC FORCE ON A MOVING CHARGE
If a particle with charge q moves with velocity v through a magnetic field B, it will experience a magnetic force, FB, with magnitude:
FB = |q|vB sin θ (1)
where θ is the angle between v and B. From this equation, we can see that if the charge is at rest, then v = 0 immediately gives us FB = 0. This tells us that magnetic forces only act on moving charges. Also, if v is parallel (or antiparallel) to B, then FB = 0 since, in either of these cases, sin θ = 0. So, only charges that cut across the magnetic field lines will experience a magnetic force. Furthermore, the magnetic force is maximized when v is perpendicular to B, since if θ = 90°, then sin θ is equal to 1, its maximum value.
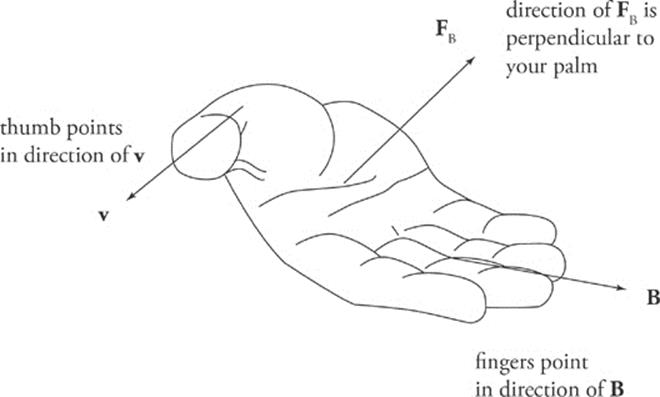
The direction of FB is always perpendicular to both v and B and depends on the sign of the charge q and the direction of v × B (which can be found by using the right-hand rule).
If q is positive, use your right hand and the right-hand rule.
If q is negative, use your left hand and the left-hand rule.
Whether you use the right-hand rule or the left-hand rule, you will always follow these steps:
1. Orient your hand so that your thumb points in the direction of the velocity v.
2. Point your fingers in the direction of B.
3. The direction of FB will then be perpendicular to your palm.
Think of your palm pushing with the force FB; the direction it pushes is the direction of FB.
Right-Hand Rule:
For determining the direction of the magnetic force, FB, on a positive charge
Note that there are fundamental differences between the electric force and magnetic force on a charge. First, a magnetic force acts on a charge only if the charge is moving; the electric force acts on a charge whether it moves or not. Second, the direction of the magnetic force is always perpendicular to the magnetic field, while the electric force is always parallel (or antiparallel) to the electric field.
Example 13.1 For each of the following charged particles moving through a magnetic field, determine the force acting on the charge.
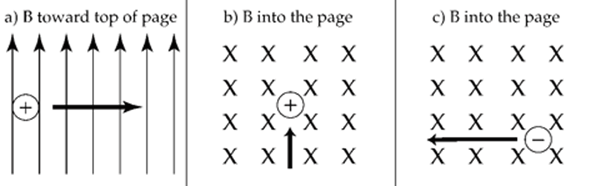
Solution.
a) If you point your fingers to the top of the page and thumb to the right of the page, your palm should point out of the page. The force is out of the page.
b) If you point your fingers into the page and thumb to the top of the page your palm should point to the left of the page. The force is to the left of the page.
c) If you point your fingers into the page and thumb to the left of the page, your palm should point to the bottom of the page. The force of a positive charge would be toward the bottom of the page, but because this is a negative charge, the force points up.
The SI unit for the magnetic field is the tesla (abbreviated T) which is one newton per ampere-meter. Another common unit for magnetic field strength is the gauss (abbreviated G); 1 G = 10–4 T.
Example 13.2 A charge +q = +6 × 10–6 C moves with speed v = 4 × 105 m/s through a magnetic field of strength B = 0.4 T, as shown in the figure below. What is the magnetic force experienced by q?
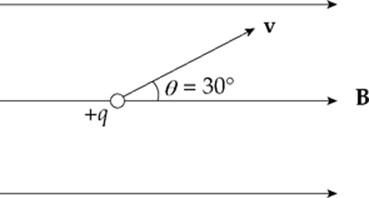
Solution. The magnitude of FB is
FB = qvB sin θ = (6 × 10–6 C)(4 × 105 m/s)(0.4 T) sin 30° = 0.48 N
By the right-hand rule, the direction is into the plane of the page, which is symbolized by ×.
Example 13.3 A particle of mass m and charge +q is projected with velocity v (in the plane of the page) into a uniform magnetic field B that points into the page. How will the particle move?
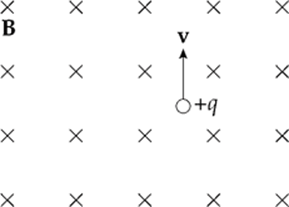
Solution. Since v is perpendicular to B, the particle will feel a magnetic force of strength qvB, which will be directed perpendicular to v (and to B) as shown:
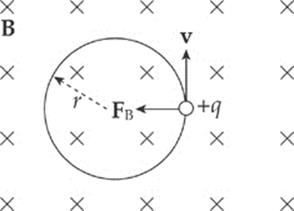
Since FB is always perpendicular to v, the particle will undergo uniform circular motion; FB will provide the centripetal force. Notice that, because FB is always perpendicular to v, the magnitude of v will not change, just its direction. Magnetic forces alone cannot change the speed of a charged particle, they can only change its direction of motion. The radius of the particle”s circular path is found from the equation FB = FC:
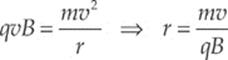
Example 13.4 A particle of charge –q is shot into a region that contains an electric field, E, crossed with a perpendicular magnetic field, B. If E = 2 × 104 N/C and B = 0.5 T, what must be the speed of the particle if it is to cross this region without being deflected?
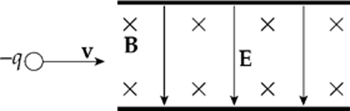
Solution. If the particle is to pass through undeflected, the electric force it feels has to be canceled by the magnetic force. In the diagram above, the electric force on the particle is directed upward (since the charge is negative and E is downward), and the magnetic force is directed downward by the right-hand rule. So FE and FB point in opposite directions, and in order for their magnitudes to balance, qE must equal qvB, so v must equal E/B, which in this case gives
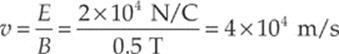
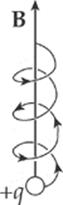
Example 13.5 A particle with charge +q, traveling with velocity v, enters a uniform magnetic field B, as shown below. Describe the particle”s subsequent motion.

Solution. If the particle”s velocity were parallel to B, then it would be unaffected by B. If v were perpendicular to B, then it would undergo uniform circular motion (as we saw in Example 13.2). In this case, v is neither purely parallel nor perpendicular to B. It has a component (v1) that”s parallel to B and a component (v2) that”s perpendicular to B.
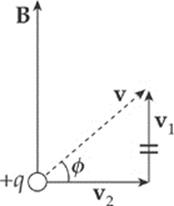
Component v1 will not be changed by B, so the particle will continue upward in the direction of B. However, the presence of v2 will create circular motion. The superposition of these two types of motion will cause the particle”s trajectory to be a helix; it will spin in circular motion while traveling upward with the speed v1 = v sin φ:
THE MAGNETIC FORCE ON A CURRENT-CARRYING WIRE
Since magnetic fields affect moving charges, they should also affect current-carrying wires. After all, a wire that contains a current contains charges that move.
Let a wire of length ![]() be immersed in magnetic field B. If the wire carries a current I, then the magnitude of the magnetic force it feels is
be immersed in magnetic field B. If the wire carries a current I, then the magnitude of the magnetic force it feels is
FB = BI![]() sin θ
sin θ
where θ is the angle between ![]() and B. Here, the direction of
and B. Here, the direction of ![]() is the direction of the current, I. The direction of FB can be found using the right-hand rule and by letting your thumb point in the direction in which the current flows.
is the direction of the current, I. The direction of FB can be found using the right-hand rule and by letting your thumb point in the direction in which the current flows.
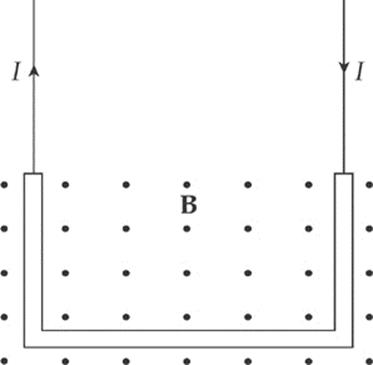
Example 13.6 A U-shaped wire of mass m is lowered into a magnetic field B that points out of the plane of the page. How much current I must pass through the wire in order to cause the net force on the wire to be zero?
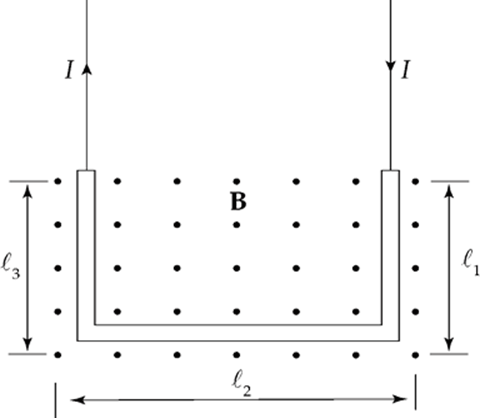
Solution. The total magnetic force on the wire is equal to the sum of the magnetic forces on each of the three sections of wire. The force on the first section (the right, vertical one), FB1, is directed to the left (applying the right-hand rule, and the force on the third piece (the left, vertical one), FB3, is directed to the right. Since these pieces are the same length, these two oppositely directed forces have the same magnitude, I![]() 1B = I
1B = I![]() 3B, and they cancel. So the net magnetic force on the wire is the magnetic force on the middle piece. Since I points to the left and B is out of the page, the right-hand rule tells us the force is upward.
3B, and they cancel. So the net magnetic force on the wire is the magnetic force on the middle piece. Since I points to the left and B is out of the page, the right-hand rule tells us the force is upward.
Since the magnetic force on the wire is I![]() 2B, directed upward, the amount of current must create an upward magnetic force that exactly balances the downward gravitational force on the wire. Because the total mass of the wire is m, the resultant force (magnetic + gravitational) will be zero if
2B, directed upward, the amount of current must create an upward magnetic force that exactly balances the downward gravitational force on the wire. Because the total mass of the wire is m, the resultant force (magnetic + gravitational) will be zero if
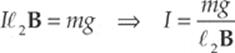
Example 13.7 A rectangular loop of wire that carries a current I is placed in a uniform magnetic field, B, as shown in the diagram below and is free to rotate. What torque does it experience?
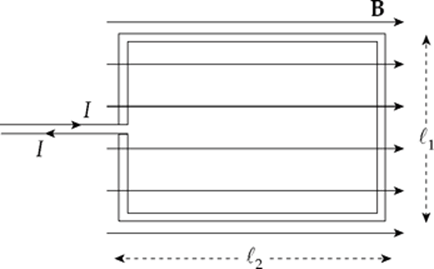
Solution. Ignoring the tiny gap in the vertical left-hand wire, we have two wires of length ![]() 1 and two of length
1 and two of length ![]() 2. There is no magnetic force on either of the sides of the loop of length
2. There is no magnetic force on either of the sides of the loop of length ![]() 2, because the current in the top side is parallel to B and the current in the bottom side is antiparallel to B. The magnetic force on the right-hand side points out of the plane of the page, while the magnetic force on the left-hand side points into the plane of the page.
2, because the current in the top side is parallel to B and the current in the bottom side is antiparallel to B. The magnetic force on the right-hand side points out of the plane of the page, while the magnetic force on the left-hand side points into the plane of the page.
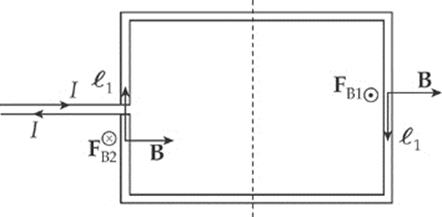
If the loop is free to rotate, then each of these two forces exerts a torque that tends to turn the loop in such a way that the right-hand side rises out of the plane of the page and the left-hand side rotates into the page. Relative to the axis shown above (which cuts the loop in half), the torque ofFB1 is
![]()
and the torque of FB2 is
![]()
Since both these torques rotate the loop in the same direction, the net torque on the loop is
τ1 + τ2 = I![]() 1
1![]() 2B
2B
MAGNETIC FIELDS CREATED BY CURRENT-CARRYING WIRES
As we said at the beginning of this chapter, the sources of magnetic fields are electric charges that move; they may spin, circulate, move through space, or flow down a wire. For example, consider a long, straight wire that carries a current I. The current generates a magnetic field in the surrounding space, of magnitude
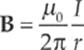
where r is the distance from the wire. The symbol µ0 denotes a fundamental constant called the permeability of free space. Its value is:
![]()
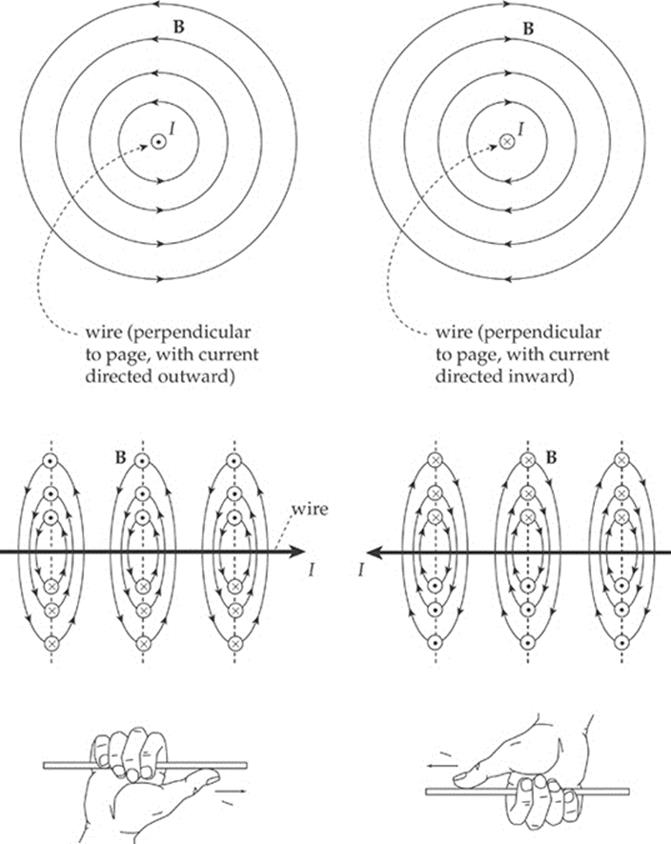
The magnetic field lines are actually circles whose centers are on the wire. The direction of these circles is determined by a variation of the right-hand rule. Imagine grabbing the wire in your right hand with your thumb pointing in the direction of the current. Then the direction in which your fingers curl around the wire gives the direction of the magnetic field line.
Example 13.8 The diagram below shows a proton moving with a speed of 2 × 105 m/s, initially parallel to, and 4 cm from, a long, straight wire. If the current in the wire is 20 A, what”s the magnetic force on the proton?

Solution. Above the wire (where the proton is), the magnetic field lines generated by the current-carrying wire point out of the plane of the page, so v0 × B points downward. Since the proton”s charge is positive, the magnetic force FB = q(v0 × B) is also directed down, toward the wire.
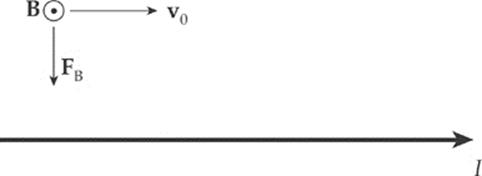
The strength of the magnetic force on the proton is
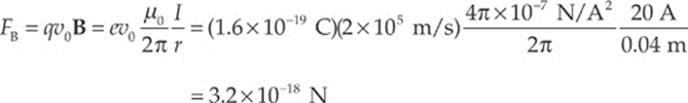
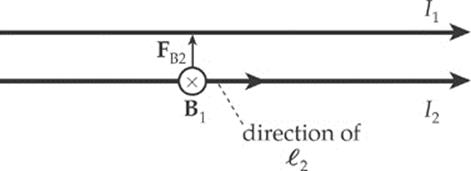
Example 13.9 The diagram below shows a pair of long, straight, parallel wires, separated by a small distance, r. If currents I1 and I2 are established in the wires, what is the magnetic force per unit length they exert on each other?

Solution. To find the force on Wire 2, consider the current in Wire 1 as the source of the magnetic field. Below Wire 1, the magnetic field lines generated by Wire 1 point into the plane of the page. Therefore, the force on Wire 2, as given by the equation FB2 = I2(![]() 2 × B1), points upward.
2 × B1), points upward.
The magnitude of the magnetic force per unit length felt by Wire 2, due to the magnetic field generated by Wire 1, is found this way:
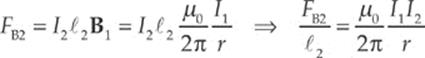
By Newton”s Third Law, this is the same force that Wire 1 feels due to the magnetic field generated by Wire 2. The force is attractive because the currents point in the same direction; if one of the currents were reversed, then the force between the wires would be repulsive.
CHAPTER 13 REVIEW QUESTIONS
Solutions can be found in Chapter 18.
SECTION I: MULTIPLE CHOICE
1. Which of the following is/are true concerning magnetic forces and fields?
I. The magnetic field lines due to a current-carrying wire radiate away from the wire.
II. The kinetic energy of a charged particle can be increased by a magnetic force.
III. A charged particle can move through a magnetic field without feeling a magnetic force.
(A) I only
(B) II and III only
(C) I and II only
(D) III only
(E) I and III only
2. The velocity of a particle of charge +4.0 × 10–9 C and mass 2 × 10–4 kg is perpendicular to a 0.1-tesla magnetic field. If the particle”s speed is 3 × 104 m/s, what is the acceleration of this particle due to the magnetic force?
(A) 0.0006 m/s2
(B) 0.006 m/s2
(C) 0.06 m/s2
(D) 0.6 m/s2
(E) None of the above
3. In the figure below, what is the direction of the magnetic force FB?
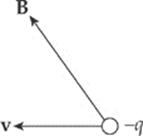
(A) To the right
(B) Downward, in the plane of the page
(C) Upward, in the plane of the page
(D) Out of the plane of the page
(E) Into the plane of the page
4. In the figure below, what must be the direction of the particle”s velocity, v?
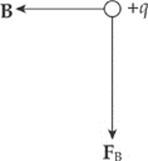
(A) To the right
(B) Downward, in the plane of the page
(C) Upward, in the plane of the page
(D) Out of the plane of the page
(E) Into the plane of the page
5. Due to the magnetic force, a positively charged particle executes uniform circular motion within a uniform magnetic field, B. If the charge is q and the radius of its path is r, which of the following expressions gives the magnitude of the particle”s linear momentum?
(A) qBr
(B) qB/r
(C) q/(Br)
(D) B/(qr)
(E) r/(qB)
6. A straight wire of length 2 m carries a 10-amp current. How strong is the magnetic field at a distance of 2 cm from the wire?
(A) 1 × 10–6 T
(B) 1 × 10–5 T
(C) 2 × 10–5 T
(D) 1 × 10–4 T
(E) 2 × 10–4 T
7. Two long, straight wires are hanging parallel to each other and are 1 cm apart. The current in Wire 1 is 5 A, and the current in Wire 2 is 10 A, in the same direction. Which of the following best describes the magnetic force per unit length felt by the wires?
(A) The force per unit length on Wire 1 is twice the force per unit length on Wire 2.
(B) The force per unit length on Wire 2 is twice the force per unit length on Wire 1.
(C) The force per unit length on Wire 1 is 0.0003 N/m, away from Wire 2.
(D) The force per unit length on Wire 1 is 0.001 N/m, toward Wire 2.
(E) The force per unit length on Wire 1 is 0.001 N/m, away from Wire 2.
8. In the figure below, what is the magnetic field at the Point P, which is midway between the two wires?
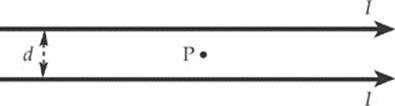
(A) 2µ0I/(πd), out of the plane of the page
(B) 2µ0I/(πd), into the plane of the page
(C) µ0I/(2πd), out of the plane of the page
(D) µ0I/(2πd), into the plane of the page
(E) Zero
9. Here is a section of a wire with a current moving to the right. Where is the magnetic field strongest and pointing INTO the page?
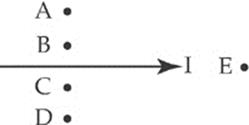
(A) A
(B) B
(C) C
(D) D
(E) E
10. What is the direction of force acting on the current-carrying wire as shown below?
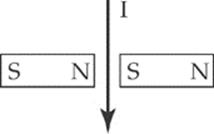
(A) to the top of the page
(B) to the bottom of the page
(C) into the page
(D) out of the page
(E) to the right of the page
SECTION II: FREE RESPONSE
1. The diagram below shows a simple mass spectrograph. It consists of a source of ions (charged atoms) that are accelerated (essentially from rest) by the voltage V and enter a region containing a uniform magnetic field, B. The polarity of V may be reversed so that both positively charged ions (cations) and negatively charged ions (anions) can be accelerated. Once the ions enter the magnetic field, they follow a semicircular path and strike the front wall of the spectrograph, on which photographic plates are constructed to record the impact. Assume that the ions have mass m.
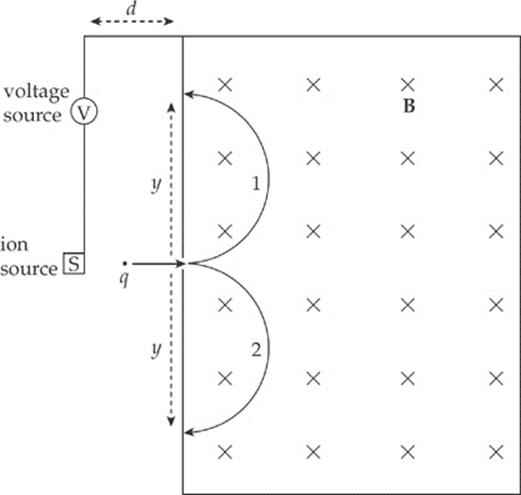
(a) What is the acceleration of an ion of charge q just before it enters the magnetic field?
(b) Find the speed with which an ion of charge q enters the magnetic field.
(c) (i) Which semicircular path, 1 or 2, would a cation follow?
(ii) Which semicircular path, 1 or 2, would an anion follow?
(d) Determine the mass of a cation entering the apparatus in terms of y, q, B, and V.
(e) Once a cation of charge q enters the magnetic field, how long does it take to strike the photographic plate?
(f) What is the work done by the magnetic force in the spectrograph on a cation of charge q?
2. A particle accelerator has a collision that results in a photon, an anti-bottom quark, and a charm quark. The magnetic field is 6.00 × 10–8 T and can be described as into the page. A photon has no charge and has an upper theoretical mass of 3.6 × 10–52 kg. The charm quark has a mass of 2.23 × 10–27 kg, a charge of 1.07 × 10–19 C and velocity of 40.1 m/s. The anti-bottom quark has a mass of the 7.49 × 10–27 kg and orbits with a radius of 92.7 m at a velocity of 41.5 m/s in a clockwise manner.
(a) What is the orbital radius of the photon?
(b) What is the orbital radius of the charm quark?
(c) What is the charge of the anti-bottom quark?
SUMMARY
· Charges moving though a magnetic field experience a force whose magnitude is given by FB = qvB sin θ and whose direction is given by the right-hand rule.
· Because the force is always perpendicular to the direction of velocity, the charge may experience uniform circular motion. It would then follow all the appropriate circular motion relationships and orbit in a radius given by r = ![]() .
.
· Because wires have charges moving though them, a wire will experience a force if placed in a magnetic field. This is expressed by FB = BI![]() sin θ. Also, a current-carrying wire will produce a magnetic field whose strength is given by B =
sin θ. Also, a current-carrying wire will produce a magnetic field whose strength is given by B = ![]() , where µ0 = 4π × 10–7 T · m/A, I is the current through the wire, and r is the radial distance from the wire.
, where µ0 = 4π × 10–7 T · m/A, I is the current through the wire, and r is the radial distance from the wire.