Homework Helpers: Physics
1 Kinematics
Answer Key
The actual answers will be shown in brackets, followed by an explanation. If you don”t understand an explanation that is given in this section, you may want to go back and review the lesson that the question came from.
Lesson 1–1 Review
1. [displacement]—You can”t completely describe an object”s displacement without indicating the direction.
2. [98 m]—The direction that she traveled is not important, because the question only asks us for the distance that she traveled (33 m + 42 m + 23 m = 98 m).
3. [36 m at 66° north of east]—This question asks for a displacement, so we must indicate the change of position and the direction. We can find the overall change in position using the Pythagorean theorem:
![]()
which we will round to 36 m
To find the direction, we find the angle formed between the resultant vector and the displacement to the east.
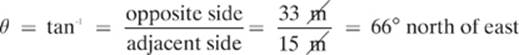
Lesson 1–2 Review
1. [velocity]—Remember: Velocity is a vector. Speed is scalar.
2. [yes]—When an object changes direction, the velocity will change, even if the speed is constant.
3. [130 m/s at 16° west of south]—We can find the magnitude of the velocity using the Pythagorean theorem,
![]()
and the direction with the inverse tangent,
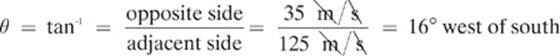
Lesson 1–3 Review
1. 
2. 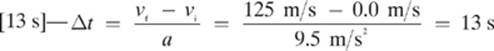
3. [yes]—If an object with a negative velocity experiences a negative acceleration, it speeds up. The negative sign simply implies a direction.
4. [yes]—Remember: Acceleration is defined as a change in velocity and velocity is a vector quantity. This means that if the car changes its direction, it is changing its velocity. By definition, this requires acceleration.
5. [9.25 m/s]—vf = + vi + aΔt = 18.0m/s + (–2.50m/s2)(3.50s) = 9.25m/s
Lesson 1–4 Review
1. ![]()
2. 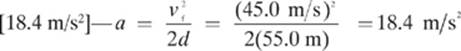
3. 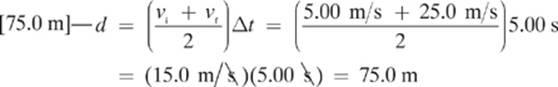
Note, the 2 in the denominator of our equation is considered a counting number, not a measurement, so we don”t use it for determining the number of significant digits in our answer.
Lesson 1–5 Review
1. [free fall]—True free fall only occurs when the only unbalanced force acting on it is gravity.
2. [The velocity will equal zero; the acceleration will equal g.]—Remember that the velocity decreases as the ball goes up, until it reaches zero at the top of its flight. The velocity will then increase on the way down. The acceleration is constant. During the entire flight, the ball experiences the acceleration due to gravity, –9.81 m/s2.
3. ![]()
Lesson 1–6 Review
1. [velocity]—Remember: We find the slope of the line by dividing the change in the y-axis by the change in the x-axis. Because the y-axis on this type of graph represents position and the x-axis represents time, we are really finding the displacement over the change in time, or velocity, when we take the slope.
2. [a line segment with a negative slope]—Remember to always subtract the initial position from the final position (Δy = yf – yi) when using the slope formula. This way, you get a negative value for the change in position when you should.
3. [a straight line segment]—Only a horizontal line represents an acceleration of zero, but any straight line segment shows uniform acceleration.
Lesson 1–7 Review
1. [zero]—We ignore air resistance, so the only unbalanced force acting on the object, after the initial projection, is gravity. In other words, the projectile is in free fall.
2. [Neither. They would hit the ground at the same time.]—The first bullet only appears to be in the air longer because it travels a great distance in the y dimension. Remember: Both bullets are in free fall, with an initial velocity of zero in the y dimension. The amount of time that each bullet will be in the air can be found with the same calculation.
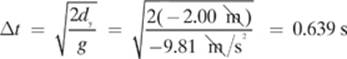
3. [6.54 m/s]—viy = vi sinθ = (12.0 m/s)(sin 33.0°) = 6.54 m/s
Chapter 1 Examination
1. [e. scalar]—A scalar quantity, such as speed or distance, requires that no direction be specified.
2. [g. mechanics]—Classical, or Newtonian, mechanics deals with the motion of relatively large objects; quantum mechanics deals with the motion of particles.
3. [c. velocity]—Velocity is the vector counterpart to speed.
4. [i. component vector]—Remember: “Component” vectors “combine” to form resultant vectors.
5. [f. acceleration]—Remember that unlike the common definition for acceleration, in physics, an object can accelerate without changing its speed, because a change in direction is also a change in velocity.
6. [d. free fall]—An object such as a parachute that is being slowed by significant air resistance is not in free fall.
7. [a. distance]—You can describe the distance you walked without mentioning a direction. A person may say, “I ran 5 miles today!” and you know what he or she means.
8. [c. m/s2]—Velocity is measured in m/s, and a change in time is measured in seconds.
![]()
9. [b. speed up]—An acceleration is a change in velocity, so answers A and D don”t make sense. Answer c makes no sense because how can an object at rest slow down? The object will speed up, increasing its velocity in the direction that has been designated as negative.
10. [a. 11.0 m]—To find the total distance, we simply add all of the individual distances. 3.0 m + 6.0 m + 2.0 m = 11.0 m.
11. [b. 0.0 m]—The dog ends up in exactly the same spot, so its displacement is zero.
12. [d. position]—An object at constant speed or velocity is still in motion, provided the speed is not zero. An object with an acceleration of zero can certainly be in motion. Only the position of an object in motion needs to change.
13. [a. –2.0 × 101 m/s]—
vf = vi + gΔt = 0.0 m/s + (–9.81 m/s2)(2.0 s) = – 2.0 × 101 m/s.
Remember: The negative sign indicates that the velocity is downward.
14. ![]()
15. ![]()
16. [4 m/s]—You must find the slope of the line at that point. You can select any two points from the straight-line segment and use the slope formula.
![]()
17. [12 m]—We can look at the y-axis and see that the car went from 0 m to 12 m during this period of time.
18. [3 s]—A slope of zero represents a velocity of zero. The slope becomes zero at 3 s.
19. [6 s to 9 s]—From 6 seconds to 9 seconds, the slope of the line is negative, as shown by the slope formula.
![]()
20. [8 m]—Tracing back to the y-axis, we can see that the car has a displacement of 8 m.
21. [0.33 s, 0.50 m]—First, convert the height of the table to meters.

22. 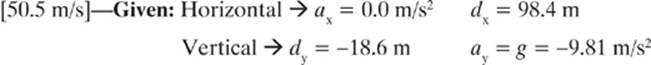
First, let”s figure out how long the car was in the air.
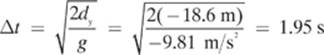
It traveled 98.4 m in this time, so its initial velocity was
![]()
23. [13.2 m]—First, we will resolve the initial velocity into its x and y components.

Now, we use the viy to find out how long the ball spends going up.
![]()
The ball spends an equal amount of time coming down, so the total time of flight is 2 × 0.792 s = 1.58 s.
Finally, we use this time of flight and the velocity in the horizontal to determine how far the ball flies.
![]()
24. 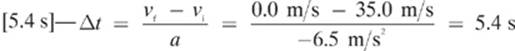
25. ![]()
The answer to our calculation was negative because we solved for the displacement of the balloon, which fell approximately 40 meters in the downward direction. However, the question asked about the height of the building, so we answer with the absolute value.