Homework Helpers: Physics
2 Forces and the Laws of Motion
Lesson 2–5: Motion Along a Horizontal Surface
In this lesson we get to cover some of my favorite problems. I always enjoy teaching this section because, at this point, the problems start getting sophisticated enough to make them pretty interesting. To solve these problems involving motion on a horizontal surface, students need to make use of a number of skills that they practiced earlier. It becomes necessary to move away from the mechanical type of problem-solving that may feel “safe,” to the more challenging type of problem-solving, which requires logic and understanding.
Invariably, when students get to this lesson they want a formula that they can use in all situations. Unfortunately, although most of these problems all come down to Newton”s second law, there is no “master formula” that can be used for every situation. You need to learn to analyze each particular situation and choose the appropriate formulas. It is analogous to a mechanic or carpenter choosing the appropriate tool for a given situation. In this way, each new formula that you learn is like a new tool that you can add to your mental toolbox, for use when you need it.
Coefficient of Friction
Let”s add another tool to that box right now. Have you ever been walking on a driveway and you suddenly step on a patch of ice and slip? What is the difference between the two surfaces? There is less friction between your foot and the ice. Your foot slips more freely, and you fall as a result.
But what is friction? We did an example of a problem with friction in Lesson 2–1, but we didn”t really go into much detail. Friction is a force between two objects that are in contact with each other, exerted parallel to the surface of contact. When the two objects are not moving relative to each other, this force is called static friction. When one object is moving relative to the other, this force is called kinetic friction. You may recall a situation where you have noticed the difference between these two kinds of friction. Have you even needed to push a heavy object, say a desk or dresser, across a floor? Did you notice that it is hard to start the object moving, but once the object is in motion, it takes less effort to keep the object moving? This is because the force of kinetic friction is always less than the force of static friction, so the force you needed to overcome to get the object moving is less than the force that you need to overcome to keep it moving.
What determines the magnitude of the friction between two objects? The first thing, as you might imagine from our examples involving ice, is the nature of the materials in contact. The second has to do with the normal (perpendicular) force between the objects, which you might think of as how hard the objects are pressed together. If you touch your hands lightly together and rub them back and forth, they slide more freely than if you press them together harder. In the same way, there is more friction between a heavy desk and a wood floor than there would be if you emptied the drawers of the desk and made it lighter.
When you divide the force of static friction by the normal force between two stationary objects that are in contact, you get the coefficient of static friction, as shown here:
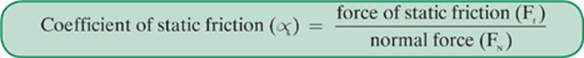
When you divide the force of kinetic friction by the normal force between objects that are in contact and motion relative to each other, you get the coefficient of kinetic friction, as shown here:
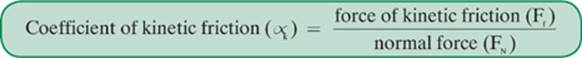
The greater the force of friction between two objects, the higher the coefficient of friction will be.
Let”s try a couple examples that deal with coefficient of friction.
Example 1
A desk with a mass of 75.0 kg sits on a floor, and the coefficient of static friction between the two surfaces is 0.40. How much force must someone apply in a direction horizontal to the surface of the floor to get the desk moving?
Can you see how to solve this problem? We will use the mass of the desk and the acceleration due to gravity to find the weight of the desk. The magnitude of this weight will be equal to the normal force. We will then use the normal force and the coefficient of static friction to determine the maximum value of the force of static friction. The force required to move the desk will be greater than this maximum value for the force of static friction.
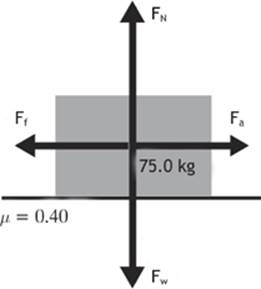
Figure 2.6
Given: m = 75.0 kg g = 9.81 m/s2 μs= 0.40
Find: FN and then Ff
Solution:
Normal force = FN = –Fw = –mg
= –(75.0 kg)(–9.81 m/s2)
= 736 N
Static friction = Ff = μs FN
= (0.40)(736 N) = 290 N
The desk will begin to slide if a force that is greater than this maximum value of the force of static friction is applied, so our answer is greater than 290 N.
Now let”s try a slightly more complicated problem.
Example 2
A boy exerts a horizontal force of 12.0 N on a 20.0 N box to slide it across a table where the coefficient of kinetic friction between the surfaces is 0.34. Find the acceleration on the box.
Given: Fw = –20.0 N g = –9.81 m/s2 Fa = 12.0 N μk = 0.34
FN = –FW = 20.0N
Find: a
Can you come up with a plan to solve this problem? It asks for the acceleration, so we can use Newton”s second law (Fnet = ma) for that. We will need to find the mass of the box, but that will be as easy as dividing the weight of the box by the acceleration due to gravity (g). The normal force is easy as well, because in this case it will be equal to the magnitude of the weight of the box. To find the net force (Fnet) we will first need to find the force of friction (Ff) using the coefficient of kinetic friction and the normal force. We give the friction a negative sign because it opposes the motion of the box. If we gave the force of friction the same sign as the applied force, the friction would actually help the boy accelerate the box!
Solution:
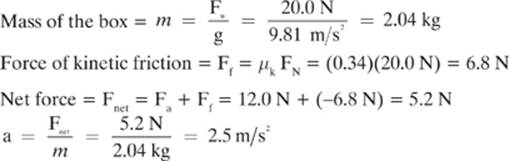
The fact that the acceleration has the same sign and therefore the same direction as the applied force means that the box will speed up. If the applied force were less than the force of kinetic friction, the box would slow down.
Now that we have gone over the basics, let”s try a more difficult problem. Let”s imagine a situation where a girl is dragging a sled over the ground by exerting a force on a rope that makes an angle above the horizontal. In such a situation, not all of the force that the girl is exerting is parallel to the ground, opposite to the friction. We must resolve the original applied force into its x and y components. The x component of the force will be working against the force of friction, while the y component of the applied force will work against the weight of the sled, decreasing the normal force, which will, in turn, decrease the force of friction.
Example 3
A girl is pulling a sled with a mass of 16.0 kg across a level patch of grass by exerting a force of 22.0 N along a rope that forms an angle of 33.0° above the ground. If the coefficient of kinetic friction between the sled and the grass is 0.25, find the acceleration of the sled.
Given: m = 16.0 kg Fa = 22.0 N at 33.0° above the horizontal μk = 0.25
Find: a
As I mentioned in the introduction to this lesson, there is a lot to some of these problems. You can”t just look up a formula and plug in the given information. You need to slow down, think, and formulate a plan for solving them. This problem asks us to find the acceleration of the sled, so we know that we will be using Newton”s second law. That means that we will need to find the net force on the sled. In our previous example, the force of weight and the normal force were equal and opposite, leaving us with a net force of zero in the vertical, so we only considered the force parallel to the ground. Finding the net force in this problem is a bit more complicated, because now we must consider an extra vertical force, the y component of the applied force. As the girl pulls on the rope, she is taking on some of the weight of the sled, decreasing the force it will exert on the ground, and the normal force. We will still end up with a net force of zero perpendicular to the ground, but we must take into account how the vertical component of the applied force affects the force of kinetic friction.
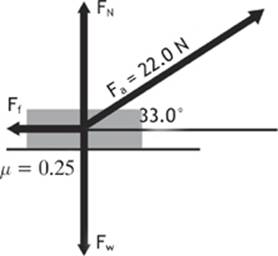
Figure 2.7
Solution:
Let”s begin by finding the x and y components of the applied force, using the trigonometry functions with which you should now be familiar.
Force applied in the
x = Fax = Fa cos θ = (22.0 N)(cos 33.0°)
= 18.5 N
Force applied in the
y = Fay = Fa sin θ = (22.0 N)(sin 33.0°)
= 12.0 N
Now let”s find the normal force. Remember: The force of weight is directed downward, and the vertical component of the applied force is directed upward. When we add these forces let”s make the weight negative, so they work against each other.
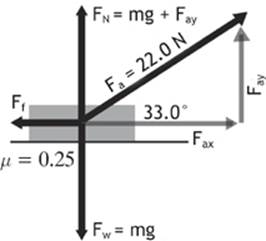
Figure 2.8
Normal force = FN = –(Fw + Fay) = –(mg + Fay)
= –(16.0 kg)(–9.81 m/s2) + (12.0 N) = 145 N
We can use the normal force and the coefficient of kinetic friction to find the force of kinetic friction.
Force of kinetic friction = Ff = μk FN = (0.25)(145 N) = 36.3 N
We will add the force applied in the x to the force of friction to find the net force acting on the sled. Of course, because the force of friction is working against the applied force, we will make it negative.
Net force = Fnet = Fax + Ff = 18.5 N + (–36.3 N) = -17.8 N
Remember: The negative value of our answer tells us that the force of friction is greater than the force the girl is applying in the horizontal, and in the opposite direction. This means that the sled is going to be slowing down. We find the acceleration here:
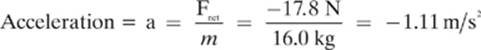
Will the sled stop? That depends on whether or not the girl can apply a greater force, or if she moves off the grass onto another surface. What would happen if she changes the angle of the rope instead of changing the force she exerts? Decreasing the angle would increase the component of the force along the horizontal, but it would also decrease the force exerted in the vertical. Decreasing the force exerted in the vertical will actually increase the normal force and the force of friction! Would decreasing the angle between the rope and the ground make it easier or harder for the girl to pull the sled over the grass? Let”s see what happens if she changes the angle between the rope and the horizontal to 10.0°. This would be a good opportunity for you to try the problem on paper, and check your answer against mine.
Example 4
A girl is pulling a sled with a mass of 16.0 kg across a level patch of grass by exerting a force of 22.0 N along a rope that forms an angle of 10.0° above the ground. If the coefficient of kinetic friction between the sled and the grass is 0.25, find the acceleration of the sled.
Given: m = 16.0 kg Fa = 22.0 N at 10.0° above the horizontal μk = 0.25
Find: a
Solution:
Force applied in the x = Fax = Fa cos θ = (22.0 N)(cos 10.0°) = 21.7 N
Force applied in the y = Fay = Fa sin θ = (22.0 N)(sin 10.0°) = 3.82 N
Normal force = FN = –(Fw + Fay) = –(mg + Fay)
= –((16.0 kg)(–9.81 m/s2)) + (–3.82 N) = 153 N
Force of kinetic friction = Ff = μk FN = (0.25)(153 N) = 38.3 N
Net force = Fnet = Fax + Ff = 21.7 N + (–38.3 N) = -16.6 N
![]()
The sled is still slowing down, but at a lesser rate. So decreasing the angle between the rope and the ground would benefit the girl.
You may want to practice this problem a few times, changing the angle of the rope or the applied force each time. Keep in mind that the acceleration will not always be the unknown. Sometimes the coefficient of friction is the unknown and the acceleration is given. You need to learn to adapt your train of thought to the given situation.
When you feel ready, go on to the review problems.
Lesson 2–5 Review
1. _______________ is the force of friction between two objects that are not in motion relative to each other.
2. _______________ is the ratio of the force of static or kinetic friction to the normal force.