Homework Helpers: Physics
2 Forces and the Laws of Motion
Answer Key
The actual answers will be shown in brackets, followed by an explanation. If you don”t understand an explanation that is given in this section, you may want to go back and review the lesson that the question came from.
Lesson 2–1 Review
1. [net force]—You may also see the terms resultant force or total force used interchangeably with net force.
2. [5.5 N]—The weight of the book and the normal force exerted by the table on the book will add up to 0 N in the vertical (y) dimension. In the horizontal, we have an applied force of 12.0 N and a force of friction of 6.5 N. Because friction opposes the motion of the book, I will make it negative as I add the forces.
Fnet = Fa + Ff = 12.0 N +(–6.5 N) = 5.5 N.
3. [9.43 N]—The question only asks for the magnitude of the force, which means that we don”t need to report direction. Because the two component forces act at right angles to each other, we can solve for the resultant force using the Pythagorean theorem.
![]()
Lesson 2–2 Review
1. [Inertia]—To be sure that you understand the concept of inertia, think of some real-life situations where your own inertia is apparent.
2. [There is a net force on the rock.]—An object”s inertia will allow it to maintain uniform, straight-line, motion unless acted upon by an unbalanced force. The fact that the rock is changing direction means that it is accelerating and must have a net force on it. The force exerted along the string is an example of what is called a centripetal or “center seeking” force.
3. [A 35.0 kg boy]—More massive objects have greater inertia. Inertia can be used to measure mass.
Lesson 2–3 Review
1. [Weight]—Remember: The formula for weight (Fw = mg) is really just a specific application of Newton”s second law (F = m a).
2. 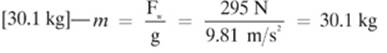
3. ![]()
4. [One newton is the amount of force required to accelerate a mass of one kilogram at a rate of one meter per second squared.]—
1.0 N = 1.0 kg × 1.0 m/s2
Lesson 2–4 Review
1. [24.0 N]—Because the question only asks for the magnitude of the force exerted on the rock by the driveway, we don”t need to worry about signs. The normal force will be equal to the weight of the rock.
FN = –FW = –mg = –(2.45 kg)(–9.81 m/s2) = 24.0 N
2. [no]—Newton”s third law tells us that the force that the car exerts on the garbage can will be equal and opposite to the force that the garbage can exerts on the car. The two objects have very different masses, so they will experience very different accelerations, as given by Newton”s second law:
![]()
3. [The thin ice is incapable of exerting a force that is equal and opposite to the person”s weight, so there is an unbalanced downward (net) force. Therefore, the person accelerates down through the ice.]—The unbalanced downward force before the ice breaks would be equal to the force of weight (Fw) + the force that the ice exerts on the person (Fice). Fnet = Fw + Fice. The Fice would be upwards (positive) and the Fw would be downward (negative).
Lesson 2–5 Review
1. [Static friction]—Static means “unchanging” or “unmoving.”
2. [Coefficient of friction]—Rough surfaces will have greater coefficients of friction than smooth surfaces.
Chapter 2 Examination
1. [c. friction]—You may have selected “d. contact force,” but this definition was more specific. Friction was a better answer because it is a specific type of contact force.
2. [e. weight]—You may have selected “g. field force” but that answer is too general.
3. [b. net force]—The term resultant force is sometimes referring to the same thing.
4. [h. inertia]—Because of inertia, an object at rest tends to remain at rest and an object in motion tends to remain in motion.
5. [a. 1 N]—We need to use Newton”s second law, F = ma, to solve this one.
However, notice that they give us the weight of the object, rather than the mass. So we need to use Fw = mg to find the mass of the object first.

6. ![]()
7. ![]()
8. 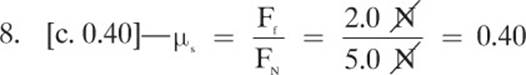
9. [c. the same]—Newton”s third law tells us that the forces will be equal and opposite.
10. [b. 1.4 N]—Fx = F cosθ = (2.8 N)(cos 60.0°) = 1.4 N
11. [a. 3.0 × 102 N]—To get the desk moving, we must apply a force equal in magnitude to the maximum static friction.
F = Ff = μs FN = (0.45)(670 N) = 301.5 N = 3.0 × 102 N
12. [b. 9.22 N]—The two component forces are acting perpendicular to each other, so the resultant vector of 11.0 N will form the hypotenuse of the right triangle. We can solve this problem with the Pythagorean theorem.
![]()
13. [a. 0°]—At 45° or 90°, only a component of one force will be added to the other. At 180°, the students will be working against each other.
14. [a. 11.0 N]—If the angle between them is 180°, then they are working against each other. We make one negative and then add them together.
16.0 N + (–5.0 N) = 11.0 N
15. [11.3 m/s2]—We want to use Newton”s second law of motion, Fnet = ma, to find the acceleration of the book. In order to do this, we need to find the net force in the x dimension. The only forces acting in the x dimension are the applied force (Fa) and the force of friction (Ff). We have the applied force, but we don”t yet have the force of friction. We do, however, have the coefficient of friction (μk) and we can assume that the normal force will be equal in magnitude to the weight of the book (Fw), because the surface is horizontal.
force of friction (Ff) = μk FN = μk FW = (0.35)(10.0 N) = 3.5 N
Remember that the force of friction opposes the applied force, so I will give it a negative sign in the next formula.
net force (Fnet) = Fa + Ff = 15.0 N + (–3.5 N) = 11.5
Now we can find the mass of the book in kilograms.
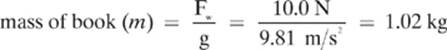
We now have everything we need to find the acceleration of the book.
![]()
Note: You may have ended up with an answer of 11.6 m/s2if you solved the problem with one equation or maintained more significant digits at each step.
16. [0.650]—If you don”t think that you have enough information to solve this problem, then you probably missed an important “implied given.” When we said that the wood block is sliding with “uniform velocity,” meaning with an acceleration of zero, we are implying that the net force parallel (Fnetx) to the surface of the incline must also be zero. Because the only two forces acting parallel to the surface are the force of friction (Ff) and the parallel component of the weight of the block (Fwx), they must be equal and opposite in order to add to zero.
Fnetx = Fwx + Ff = 0 N
So, our plan should be to find the components of the weight and use the parallel component (Fwx) to find the force of friction (Ff) and the perpendicular component (Fwy) to find the normal force (FN). We will then have enough to solve for the coefficient of friction.
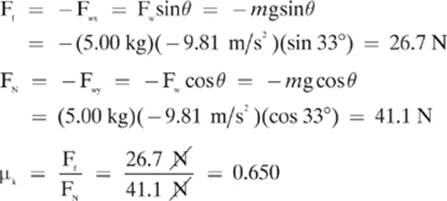
17. [133 N]—F wx = mg sin θ = (22.0 kg)(9.81 m/s2)(sin38°) = 133 N
18. [1.47 m/s2]—From Newton”s second law, we know that a ![]() .
.
We can find the net force by adding the applied force to the force of friction, where we make friction negative.
Fnet = Fa + Ff = 50.0 N + (–20.0 N) = 30.0 N
We can find the mass of the couch by dividing its weight by the acceleration due to gravity.
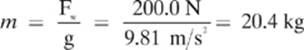
Putting it all together, we get:

19. [1,090 N]—It is important to note that the elevator is accelerating. A scale shows the normal force (FN) that the spring in it is exerting in reaction to the force that is being exerted on it. If the elevator were moving with constant velocity, the man would be exerting a force equal to his weight (Fw) on the scale, and the scale would exert an equal and opposite (FN = –Fw) force. Because the elevator is accelerating, the scale is sort of being pushed into the man”s feet. We need to multiply the acceleration of the elevator (ae) by the mass of the man, and add that to the force of weight.
The mass of the man will be:
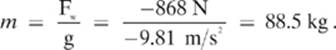
The force shown by the scale will be:
FN = –FW + mae = 868 N + (88.5 kg)(2.50 m/s2) = 1,090 N
Note: It is easy to become confused by the sign conventions involved in this type of problem and, in fact, some people might take issue with the way that I used signs in my solution. The important thing to remember is that the forces work together in this problem, resulting in a total force that is greater than the weight of the man. This matches what you experience in real life. As an elevator starts moving (accelerating) upward, you feel as though you are being pressed into the floor.
20. [532 N]—FN = –FW + mae = 868 N + (88.5 kg)(–3.8 m/s2) = 532 N