Homework Helpers: Physics
3 Work, Energy, Power, and Momentum
Lesson 3–2: Energy
In the last lesson, we introduced work by first defining energy as the ability to do work. Now that you understand the concept of work better, you may also have a better understanding of energy. A moving car has energy, and it can do work (exert a force over a distance) on an object that it strikes. A compressed spring has energy, and it can exert a force and displace an object as it expands. A heavy chandelier has energy, and it can fall off the ceiling and do work on objects it lands on, exerting a force and displacing it downward. Objects with energy can do work, and whenwe do work on objects, we can give them energy. Work and energy are intimately linked. So much so, in fact, they are both measured in the same units: joules.
Gravitational Potential Energy
Toward the end of our last lesson, we went over an example involving a crane lifting an object. When we lift objects, we use energy to do work on them. Where does the energy that we use go? The energy used gets stored by the object, in a form called gravitational potential energy. Gravitational potential energy is the stored energy that an object has due to its own mass and its position above a reference point.
Gravitiational Potential Energy
The stored energy that an object possesses due to its mass and its height above a reference point.
Gravitational Potential Energy = mass × acceleration due to gravity × height P.E.g = mgh
When determining the gravitational energy that an object has, it is important to pay attention to the reference point from which the height is being measured. For example, if you have a can of paint on a shelf and the shelf is on the third floor of a building, you could measure the height of the can with respect to the floor of the room, or to the ground outside the building.
Let”s look at an example of a problem that will clearly illustrate the relationship between work and gravitational potential energy.
Example 1
A girl lifts a 5.00 kg toy to a height of 0.75 meters in order to place it on a shelf. Determine (a) how much work (W) the girl does on the toy to lift it, and (b) how much gravitational potential energy (P.E.g) the toy has while resting on the shelf, with reference to the floor.
Given: m = 5.00 kg h = 0.75 m g = 9.81 m/s2
Find: W and P.E.g
Solution:
Work done on toy (W) = Fd = FW h = mgh
= (5.00 kg)(9.81 m/s2)(0.75 m) = 37 J
Gravitational Potential Energy of toy (P.E.g) = mgh
= (5.00 kg)(9.81 m/s2)(0.75 m) = 37 J
As you can see, the girl did 37 joules of work on the toy, and the toy gained 37 joules of gravitational potential energy.
Elastic Potential Energy
Another type of potential energy called elastic potential energy, can be found in springs. When a spring is compressed or stretched, it has the ability to do work in order to restore itself to its equilibrium (rest) position. Have you ever tested the shock absorbers on a car? You push down on the hood of the car, exerting a force. You do work on the car as you exert a force over a distance, pushing the front of the car down. This work gets stored as elastic potential energy, which is used to restore the car to its normal position, after you stop applying a force.
Another example of this type of energy is found when you shoot a rubber band. You stretch a rubber band over one of your fingers. As you stretch the rubber band, you are doing work on it, exerting a force over a distance. The energy that you expend is stored in the rubber band as elastic potential energy. When you release the rubber band, this energy is converted to kinetic energy, causing the band to launch toward your intended victim.
Different rubber bands and springs require different amounts of force to stretch or compress them. In each case, however, the distance that they are compressed or stretched is proportional to the force applied. The ratio of the force applied to a spring and the distance it is stretched or compressed gives us the proportionality constant (k), which is appropriately called the spring constant. The “stiffer” a spring is, the more force is required to stretch or compress it by a certain distance, the higher the value is for k. We can determine the spring constant for a spring by determining how much it will be stretched by a certain force.
If we know the spring constant of a spring, we can use a relationship called Hooke”s law to determine the force the spring will exert when it has been displaced by a certain distance.
Hooke”s Law
Elastic force = −(spring constant × displacement)
Felas = −kx
Example 2
A mass of 5.0 kg is attached to a hanging vertical spring. The spring stretches 4.0 cm beyond its equilibrium position before coming to a rest. Determine the spring constant for the spring.
Convert:
First, let”s convert centimeters to meters.
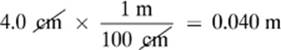
Now we find the displacement of the mass.
x = xf – xi = 0.00 m – 0.040 m = –0.040 m
Let us also find the weight of the object on the spring, which will be the force applied.
Fw = mg = (5.0 kg)(–9.81 m/s2) = 49.05 N = –49 N
Because the mass is at rest, we know that the elastic force (Felas), the force being exerted by the spring on the mass, must be equal and opposite to the force of weight.

Figure 3.2

This is a very high spring constant, indicating a very stiff spring. This makes sense for our example because a mass of 5.0 kg (weighing about 11 pounds) only stretched this imaginary spring 4.0 centimeters.
Example 3
How much force would a spring with a spring constant of 22 N/m exert when it has been compressed 0.25 m from its equilibrium (rest) position?
Given: k = 22 N/m x = 0.25 m
Find: Felas
![]()
The negative sign in our answer simply indicates that the spring will exert a force in the direction opposite to the displacement. For this reason, you will sometimes see this elastic force referred to as a restorative force.
The amount of elastic potential energy (P.E.elas) stored in a spring can be determined with the following formula.

Example 4
Calculate the elastic potential energy stored in a spring with a spring constant of 45 N/m that has been compressed 1.2 m from its equilibrium position.
Given: k = 45 N/m x = 1.2 m
Find: P.E.elas
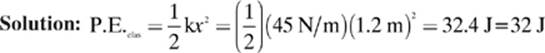
Kinetic Energy
Work doesn”t always increase the potential energy of an object. For example, if you do work on a hockey puck horizontal to the surface of the ice, you won”t increase the height or gravitational potential energy of the object. You will, however, increase the kinetic energy of the hockey puck. The kinetic energy is the energy that an object has due to its motion. Like work and gravitational potential energy, kinetic energy is measured in joules. The formula for kinetic energy is ![]()
Kinetic Energy
The energy of an object due to its motion.
![]()
Example 5
Calculate the kinetic energy of a rolling ball with a mass of 5.00 kg and a velocity of 2.50 m/s.
Given: m = 5.00 kg v = 2.50 m/s
Find: K.E.
![]()
Example 6
A toy car with a mass of 3.5 kg has 63 J of kinetic energy as it drives along the straight part of a racetrack. Calculate the velocity of the toy car.
Given: K.E. = 63 J m = 3.5 kg
Find: v

Lesson 3–2 Review
1. _______________ is the energy that an object possesses due to its motion.
2. Calculate the elastic potential energy stored in a spring with a spring constant of 25 N/m that has been compressed 0.874 m from its equilibrium position.
3. Calculate the kinetic energy of a 1.20 × 103 kg car with a velocity of 35.0 m/s.
4. Calculate the gravitational potential energy that a 6.0 kg bowling ball would have at a height of 3.0 m from the ground.