Homework Helpers: Physics

4 Rotational and Circular Motion

In Lesson 4–1 we talked about the example of children riding on a merry-go-round. We described the motion of the merry-go-round in terms of rotational motion, as it rotated around its axis. The children riding on the merry-go-round experience circular motion, as they trace out a circular path around the center of the merry-go-round.

If you were asked to describe the angular speed of the children as demonstrated in Lesson 4–1, you would find that both children would have the same angular speed, regardless of where they sat on the merry-go-round, because they complete one 360° (or 6.28 rad) circle in the same amount of time. Experience tells us that our apparent speed does depend on where we sit on these types of rides. When you ride further out from the center of the circle, you have a greater tangential speed. The tangential speed of an object is its instantaneous linear speed along the tangent to its circular path.

If a line were drawn from each child to the center of the merry-go-round, you would get the radius of the circular path in which each child travels. We can mathematically determine the tangential speed of two different children sitting on the merry-go-round and show that they can be traveling at different speeds, despite being on the same ride.

In order to explain why the two children on the same ride can have different tangential speeds, let us recall that the formula for linear speed:

It takes each child the same amount of time to complete one circular path. This amount of time is referred to as the period (T) and it is measured in seconds. In that period, each child covers a different distance. The distance that each child covers is equal to the diameter of the circle (2πr) that he or she travels around. And because the radius measured from each child to the center of the merry-go-round is different, the children will travel different distances in a given amount of time. The tangential speed of each child will be equal to the rate at which the child travels around the circle.

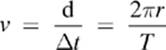
Example 1

A boy and a girl sit on a merry-go-round with a period of 3.5 seconds. The boy and girl sit 0.75 m and 0.35 m from the center of the merry-go-round, respectively. Calculate the tangential speed of each child.

As you can see from Example 1, two children sitting on the same ride can have different tangential speeds. The tangential speed (or velocity) of a child will be proportional to his or her distance from the center of rotation. The next time that you ride on a carousel, think about how your selection of a horse will influence your tangential speed.

There is a convenient formula showing the relationship between angular speed and tangential speed.

or

You can use this formula when you want to find the tangential speed of a passenger on a rotating object with a known angular speed. Or we could use the formula to find the angular speed of the merry-go-round described in Example 2 by isolating the angular speed.

Example 2

A girl sitting 0.35 m from the center of a spinning merry-go-round has a tangential speed of 0.63 m/s. Find the angular speed of the merry-go-round.

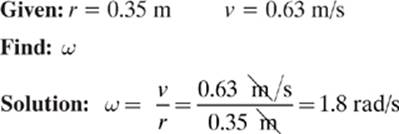
Lesson 4–3 Review

1. _________________ is the instantaneous linear speed of an object in circular motion along the tangent to its circular path.

2. A girl swings a yo-yo over her head in uniform horizontal circles with a tangential speed of 12.5 m/s. The radius of the circular path is 0.566 m. Find the period of the yo-yo.

3. Find the tangential speed of a girl sitting 0.994 m from the center of a merry-go-round with a angular speed of 4.50 rad/s.