Homework Helpers: Physics
5 Electric Charges, Forces, and Fields
Lesson 5–6: Potential Difference
A bowling ball on a shelf has more gravitational potential energy sitting on a high shelf than sitting on a low shelf. In much the same way, a charged particle will have more electric potential energy at one point in an electric field than it will have in another. If we take the difference in the electric potential energy that a test charge has between two points in the electric field and then divide by the charge on our test charge, we get the quantity known as potential difference, which is often called voltage.

or

Because electric potential energy is measured in joules and charge is measured in coulombs, potential difference is measured in J/C. An equivalent derived unit called the volt (V) has been introduced.
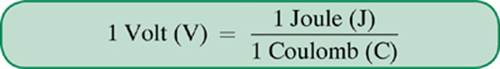
Example 1
Find the change in electrical potential energy as a proton moves through a potential difference of 1.5 V.
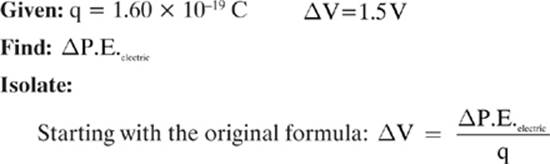
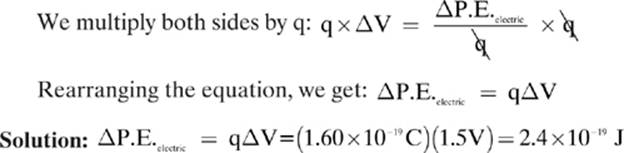
Our answer for Example 1 is so small that I”m sure you”ll understand why the unit called the electron volt (eV) is introduced. An electron volt is defined as the energy required to move an electron between two points that have a difference of potential of 1 volt. We can find the value of 1 electron volt using the same equation that we used for Example 1.
ΔP.E.electric = qΔV = (1.60 × 10–19C)(1.0V) = 1.6 × 10–19 J
So, 1 eV = 1.6 × 10–19 J
If we were asked to convert our answer for Example 1 into electron volts, we could convert as shown here:
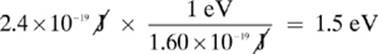
Of course, this answer makes perfect sense when you think about it. The proton has the same charge as an electron, and the potential difference in Example 1 was 1.5V, so we would need 1.5 eV to move the proton.
When we talk about batteries or cells in terms of voltage, we are really talking about the difference in potential between the positive and negative terminals. When we discuss circuits in the next chapter, you will see that we often talk about the voltage or potential difference “across” a component. In these situations we are talking about the difference in potential between a point before the current enters the component and at another point after the current leaves the component.
Combining the equation for potential difference with the relationship between electric potential energy from last lesson, ΔP.E.electric = –W, we can see how work relates to potential difference.

or
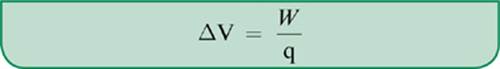
Example 2
How much work is required to move a charge of 3.0 coulombs across a potential difference of 9.0 V?
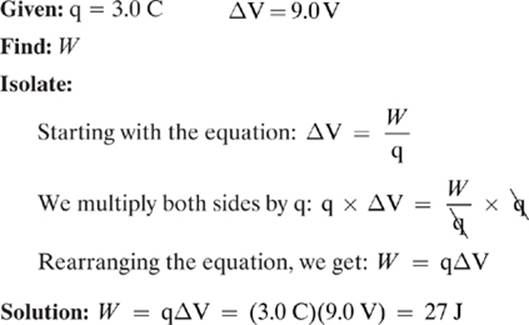
Lesson 5–6 Review
1. _______________ the energy required to move an electron between two points that have a difference of potential of 1 volt.
2. Find the change in electrical potential energy, in electron volts, as a proton moves through a potential difference of 4.5 V.
3. An alpha particle has a charge of 3.20 × 10–19 C. If it takes 3.84 × 10–18 J to move the alpha particle between two points in an electric field, find the potential difference between the two points.
Lesson 5–7: Capacitance
When I was a young teacher, with perhaps three years of experience, a couple of other teachers and I brought a group of students on a trip to Washington, D.C. At one point the students had some time to go shopping at the mall. Later, at dinner, one of the students wanted to show me the “novelty” lighter he had purchased. Some of the other students warned me not to press the button on the lighter, explaining that it produced a shock. I had experience with another novelty toy, the “joy buzzer,” which also supposedly produced a shock, but really only produced a mild vibration instead. Expecting a similar painless “shock,” I confidently pressed the button on the novelty lighter. Well, my whole arm instantly went numb, and my hand dropped as I lost control of the muscles in my arm! The lighter actually contained a powerful capacitor, capable of delivering a very real and painful shock!
Capacitors are devices that can be used to store energy in the form of separated charges. A typical capacitor consists of two parallel metallic plates, separated by an insulating material called a dielectric. When the capacitor is connected to a source of potential difference, one plate takes on a net positive charge and the other takes on a net negative charge, and the capacitor is said to be “charged.” The charged state of a capacitor will only last until a connection is made, which allows the charges to flow again. When a connection is made between the two plates of a capacitor, an electric current results, as the charges flow to reestablish equilibrium and the capacitor is discharged. As I was reminded from my run-in with the novelty lighter, a charged capacitor can be a source of potential energy.
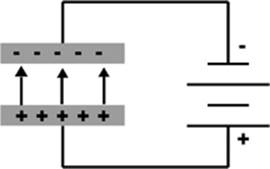
Figure 5.12

![]()
Example 1
Calculate the electrical potential energy stored in a capacitor with a magnitude of charge of 4.5 µC on each plate, and a potential difference of 1.5 V across its plates.
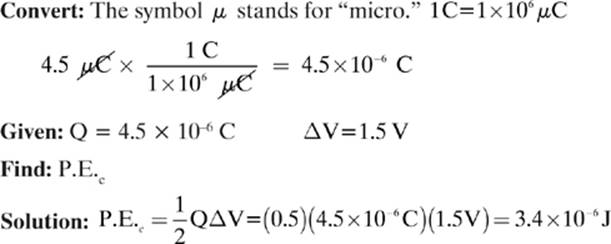
The flash in a standard camera is operated by a capacitor. The battery in the camera charges the capacitor. When a picture is taken, the capacitor discharges through the flashbulb, allowing it to get quite bright for a short time. The capacitor needs a brief period to recharge as the battery separates the charges on the plates once more.
A defibrillator, which you have probably seen on TV, if not in real life, also makes use of capacitors. The medical professional holds the two paddles of the defibrillator together until they are properly charged. He or she then yells, “Clear!” and applies the paddles to the body of the patient. A quick discharge sends electrical current into the body of the patient in an attempt to cause the heart to resume beating normally.
The ability of a capacitor to store a large amount of charge per volt is called capacitance.

or
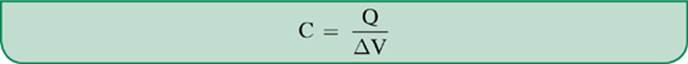
Capacitance is measured in units called farads (f), where 1 farad is equal to 1 coulomb/volt.
Example 2
Each plate on a 6.0 µf capacitor has a charge with a magnitude of 1.2 × 10–3 C on it. What is the potential difference across its plates?

If we take our last formula and isolate charge (Q), we get: Q = CV.
We can take this value for Q and substitute it into the formula we used to solve Example 1 to derive another useful formula.
![]()
Example 3
How much energy is stored in a 3.5 µf capacitor when it is connected to a 3.0 V battery?
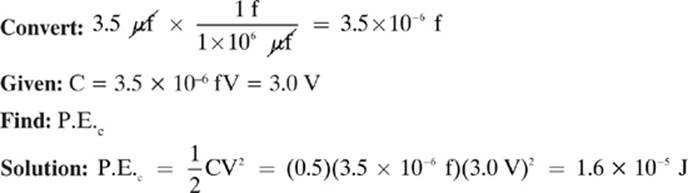
The capacitance of a capacitor is based on several factors, including the material of the plates, the dielectric material in between the plates, the size and shape of the plates, and the distance between the plates. You should remember that the capacitance of a capacitor is directly proportional to the area of one of the metal plates, and inversely proportional to the distance between them.

or
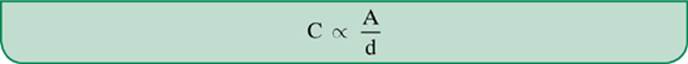
Example 4
If you double the area of both plates of a capacitor, and then double the distance between the plates, what will happen to the capacitance of the capacitor?

You would be multiplying both the denominator and numerator by 2, so the capacitance will remain the same.
A proportionality constant called the permittivity of free space, or vacuum permittivity (ε0), can be used to set the sides of the equation equal to each other.
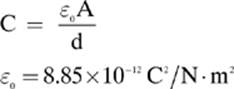
Example 5
A capacitor is made up of two parallel plates separated by a distance of 0.004 m with a vacuum between them. The area of each plate is 0.050 m2. Find the capacitance of this capacitor.
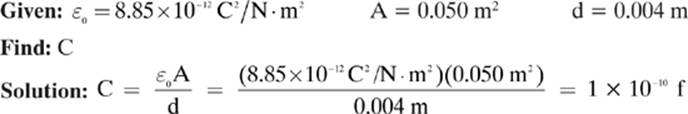
The permittivity of air is so close to that of vacuum that we use the same value for both. When a different substance, such as paper, is used as the dielectric between the plates of the capacitor, you will need to multiply the permittivity of free space by the dielectric constant (k) for that particular material, making the formula:
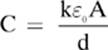
Lesson 5–7 Review
1. If you increase the distance between the charged plates of a capacitor, what will happen to its capacitance?
2. Find the capacitance of a capacitor with a potential difference of 9.0 V across its plates when each plate has a charge with a magnitude of 1.6 µC.
3. Calculate the electrical potential energy stored in a capacitor with a magnitude of charge of 2.5 µC on each plate, and a potential difference of 6.0 V across its plates.