Homework Helpers: Physics
1 Kinematics
Lesson 1–4: Constant Acceleration
In situations where the acceleration of an object is constant (including when the acceleration is zero) we can use the following group of equations to find a missing variable, such as displacement or change in velocity. These equations are so important and useful that you should become very familiar with them. Even if your instructor doesn”t require you to memorize them, you will want to make sure that you can isolate any of the potential unknowns in each of them. Many problems begin with the object at rest, in which case you can use the simplified version of the equations on the right in the table on page 42.
The ability to select a proper formula for a given situation is critical. Beginners will often wonder, Which formula do I use? The answer is really quite simple. First, you look at which quantities you are given in the situation and which quantity is your unknown. Then, you select a formula for which you have all of the variables except for the quantity that you want to solve for. You will encounter many situations where a problem can be approached from different angles and solved with different formulas, but the key will always be in identifying a formula that will bring you closer to where you want to get.
Let”s go over our first example.

Example 1
A car with an initial velocity of 8.00 m/s accelerates at a constant rate of 3.00 m/s2 until it reaches a velocity of 24.0 m/s. How far does the car travel in this time?
Before you start searching for the proper formula for solving the problem, slow down and take the time to make note of which quantities you have been given, and what the unknown is. Some students feel like this step is a waste of time at first, but they come to realize that it actually saves them time by giving them a systematic approach to solving any problem. You must be careful to interpret the word problems correctly in order to accurately identify the given quantities. In these situations, knowing which units are associated with each quantity (for example, acceleration is measured in m/s2) can be a big help.
Once you have a list of the quantities involved in the problem, selecting the proper formula should be easy, as shown here:
Given: vi = 8.00 m/s vt = 24.0 m/s a = 3.00 m/s2
Find: d
Based on what we have been given and what we want to find, the formula we select should be ![]() . For some, isolating the unknown is a challenge, so I will show the isolation for displacement.
. For some, isolating the unknown is a challenge, so I will show the isolation for displacement.
Isolation:
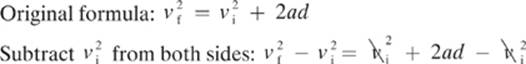

Now, let”s show a couple of more examples. Try to solve each of the following problems on your own, before checking my solutions.
Example 2
A rocket sled starts from rest and experiences a uniform acceleration of 22.5 m/s2 for 4.00 s. What will be the final velocity of the sled after this period of time?
Given: vi = 0.0 m/s a = 22.5 m/s2 Δt = 4.00s
Find: vf
![]()
Example 2 is a problem with what I call an “implied” given. When a problem states that an object “starts from rest,” what it really tells us is that the initial velocity is equal to zero. Look for this common phrase when you search a word problem for the given information.
Also, notice that we used one of the formulas for when the initial velocity is zero. If you started with the version of the formula that included the initial velocity, you would have ended up with the same answer, because the value for it was zero, as shown here.
![]()
Starting with the version of the formula where the initial velocity has been removed simply saves you a step.
Example 3
A bus has an initial velocity of 19.0 m/s. The driver slams on the brakes and the bus experiences a uniform acceleration until it comes to a stop. If the stopping distance (d) of the bus is 25.0 m, find its acceleration.
Given: vi = 19.0m/s vf = 0.00m/s d = 25.0 m
Find: a
Isolation:

The negative sign in our answer shows that the acceleration is in the direction opposite to the initial velocity, which makes sense because the bus was slowing down. Let”s try one more example together, before you move onto the practice problems.
Example 4
A go-cart with an initial velocity of 1.0 m/s accelerates uniformly at a rate of 0.25 m/s2 for a period of 12.0 s. What distance will the go-cart travel during this time?
Given: vi = 1.0 m/s a = 0.25m/s2 Δt = 12.0 s
Find: d
Solution:
![]()
Try these review problems.
Lesson 1–4 Review
1. A bus starts at rest and accelerates at a rate of 4.5 m/s2. What will be the velocity of the bus after 3.8 s?
2. An airplane starts at rest and experiences uniform acceleration until it reaches 45.0 m/s. If it travels 55.0 m during this time, find the acceleration.
3. A car with an initial velocity of 5.00 m/s accelerates uniformly to 25.0 m/s in a period of 5.00 s. How far does the car travel during this period of time?