Homework Helpers: Physics

7 Magnetism

Your experiences with magnets have likely shown you that not only do magnets come in different shapes and sizes, they also vary in a variety of “strengths.” A typical bar magnet may only be strong enough to pick up a couple of nails, but the electromagnets used in junkyards are capable of picking up cars. Just as a relatively massive planet such as Jupiter has a stronger gravitational field than one with a smaller mass, such as Mercury, each magnet has its own magnetic field strength. The strength of a magnetic field (B) at a particular point can be measured by a test charge moving through it. The magnitude of the force that a charged particle experiences as it moves perpendicularly through a magnetic field is the product of its charge, its velocity, and the strength of the magnetic field.

Force (F) =
charge of particle (q) × velocity of particle (v) × strength of magnetic field (B)
or
F = qvB

When the velocity of the charged particle is not perpendicular to the direction of the field, we must also include the sine of the angle between the velocity and field strength in our formula.

F = qvsin θ

Because the sine of a 90° angle = 1, we can use the simple formula for dealing with right angles. Note that sine 0° = 0 and sine 180° = 0, so when a charged particle moves parallel to the magnetic field, it experiences no force.

If we isolate the magnetic field strength (B) in the previous formula, we find that it is proportional to the force and inversely proportional to the charge and velocity of the particle.

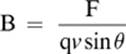
Magnetic field strength (B) is measured in derived units called tesla (T), where 1 tesla = 1 N × s/C × m = 1N/A × m.

Example 1

A proton with a velocity of 1.50 × 10⁶ m/s toward the top of the page experiences a force with a magnitude of 1.80 × 10^-13 N as it moves perpendicularly through a magnetic field. Calculate the strength of the magnetic field.

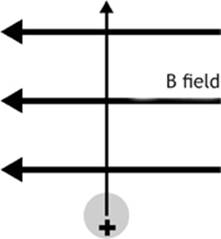
Figure 7.8

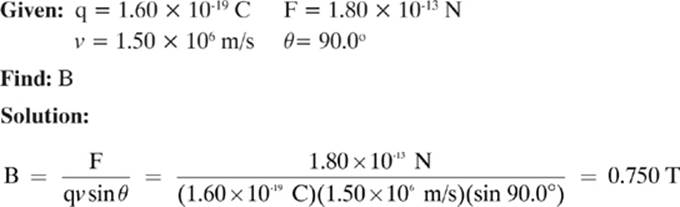
Example 2

An oxide ion travels with a velocity of 4.40 × 10⁵ m/s at an angle of 120.0° through a magnetic field with an intensity of 1.50 T. Determine the magnitude of the force acting on the ion.

Find: F

Solution: F = qvBsin θ

= (3.20 × 10^-19 C)(4.40 × 10⁵ m/s)(1.50 T)(sin 120.0°)

= 1.83 × 10^-13 N

I removed the negative sign in front of the charge on the ion because the question only asked for the magnitude of the force. If we included the sign for the charge, we would get a negative value for the force, indicating that the direction of the force would be the opposite of the force that the particle would have experienced if it had a positive charge.

Notice that the tesla is equivalent to N/A × m. We know that newtons (N) measure force and amps (A) measure current, but what would the meters (m) refer to? Because charged particles in motion experience a force when moving perpendicularly through a magnetic field, it should come as no surprise that a current-carrying wire will experience a force in a magnetic field, provided the direction of the current is not parallel to the field.

Force (F) = current (I) × length of wire (L) × magnetic field strength (B) × sin of angle between the current and the field.
or
F = ILBsin θ

As with the case of individual charged particles, when the current (I) is perpendicular to the magnetic field (B), we can use a simplified formula.

F = ILB

When the current is parallel to the magnetic field (θ = 0°), the force will equal zero.

Example 3

A wire segment with a length of 1.50 m has a steady current of 3.50 A through it. What is the magnitude of the force it would experience in a magnetic field measuring 1.20 × 10^-2 T if the wire is orientated 20.0° to the magnetic field?

Find: F

Solution:

F = ILBsin θ = (3.50 A)(1.50 m)(1.20 × 10^-2 T)(sin 20.0°) = 0.0215 N

Direction of the Force

Now that we know how to calculate the magnitude of the force experienced by charges moving through a magnetic field, let”s talk about how to determine the direction in which the force will act. You might assume that the force will be in the direction of the magnetic field, or even in the direction of the particle”s velocity, but that is not the case. The direction of the force experience by a charged object is actually perpendicular to both its motion and the direction of the magnetic field.

We use a variation of the right-hand rule, which we will call the “extended right-hand rule,” to determine the direction of the force, when we know the directions of both the field and the charges. A variety of questions may be asked to test your knowledge of this extended right-hand rule. Fortunately, these questions are likely to be limited to charges that move perpendicular to the magnetic field.

1. Point the thumb of your right hand in the direction of the velocity (v) of a positive charge. If the picture shows a negative charge, point your thumb in the opposite direction of its motion.

2. Point the index finger of your right hand in the direction of the magnetic field (B).

3. Point the middle finger of your right hand in a direction that is perpendicular to both the thumb and index finger of your right hand. The middle finger gives you the direction of the force (F).

Example 4

Look at Figure 7.9 and use the right-hand rule to determine the direction of the force experienced by a charged object moving through a magnetic field.

Step 1: Point the thumb of your right hand in the direction of the velocity (v) of a positive charge. If the picture shows a negative charge, point your thumb in the opposite direction of its motion.

The picture in Figure 7.9 shows a positive charge moving toward the top of the page, so point your thumb toward the top of the page.

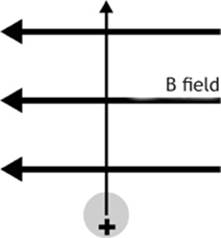
Figure 7.9

Step 2: Point the index finger of your right hand in the direction of the magnetic field (B).

The picture shows the magnetic field is directed toward the left side of the page, so point your index finger in that direction.

Step 3: Point the middle finger of your right hand in a direction that is perpendicular to both the thumb and index finger of your right hand. The middle finger gives you the direction of the force (F).

Following this instruction, your middle finger should be pointing away from, or out of, the page. If this is not the case, go through the steps again and see if you can get it.

Answer: The magnetic force is directed out of the page.

Example 5

Look at Figure 7.10 and determine the force experienced by the current carrying wire.

We handle wires in the same way that we handle individual charges.

Step 1: Point the thumb of your right hand in the direction of the velocity (v) of a positive charge. If the picture shows a negative charge, point your thumb in the opposite direction of its motion.

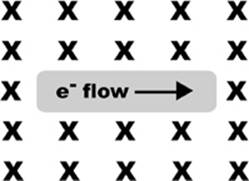
Figure 7.10

The picture shows the electron flow (negative charges) is to the right of the page, so reverse your thumb and point it to the left side of the page.

Step 2: Point the index finger of your right hand in the direction of the magnetic field (B).

The X symbols indicate that the magnetic field (B) is directed into the page, so point your index finger into the page.

Step 3: Point the middle finger of your right hand in a direction that is perpendicular to both the thumb and index finger of your right hand. The middle finger gives you the direction of the force (F).

Following this instruction, your middle finger should be pointing down, toward the bottom of the page.

Answer: The force is directed toward the bottom of the page.

Notice that our answers must be specific. Avoid using “up” or “down” as answers, because these terms aren”t specific enough on their own, and your instructor or grader won”t know if you mean “up, toward the top of the page” or “up, out of the page.” Your answer must be specific and clear.

Notice that positively charged particles will experience a force that is in the opposite direction as the force experienced by a negatively charged particle with the same velocity. This allows physicists to use magnetic fields to separate particles. As a group of particles enter a magnetic field, positive charges will be deflected one way, negatively charged particles will be deflected in the opposite direction, and neutral particles will go straight through.

Lesson 7–3 Review

1. Imagine a magnetic field directed toward the left-hand side of the page, and a positive charge moving toward the bottom of the page. What would be the direction of the force experienced by this charge?

2. A 3.50 m wire segment with a steady current of 2.30 A through it experiences a force with a magnitude of 1.12 N when positioned perpendicular to a magnetic field. What is the magnitude of the magnetic field strength?

3. A charged particle with a velocity of 1.34 × 10⁴ m/s experiences a force of 12.5 N as it travels through a magnetic field with a strength of 2.748 × 10^-15 T at an angle of 45.0°. What is the charge on the particle?