Homework Helpers: Physics

8 Waves and Light

When light strikes an object, some portion of it is absorbed and some is reflected off the surface. Some objects absorb most of the light striking their surface, and they appear dark-colored to our eyes. When an object appears to be light-colored or white, much of the light is being reflected off the surface.

What is the difference between an object that appears to be a brilliant white, and an object with a reflective surface, such as a mirror? The surface of a mirror is so smooth that it produces a regular reflection. A regular reflection occurs when light goes toward the surface in parallel,incident rays, and bounces off the surface in parallel, reflected rays. A brilliant white object can reflect as much or nearly as much light as a mirror, but the surface is not as smooth, so the reflected rays will not be parallel. Such a reflection is called an irregular, or diffuse, reflection.

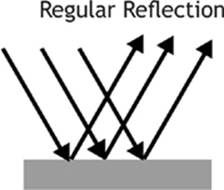
Figure 8.3

It is important to remember that it is the nature of the surface, not the nature of the light striking the surface, that determines the type of reflection that occurs. All light rays follow what is called the law of reflection. The law of reflection states that the angle of incidence will always be equal to the angle of reflection. The angle of incidence is formed between the incident (incoming) ray of light and the normal (perpendicular) to the medium boundary. The angle of reflection is the angle between the reflected (outgoing) ray and the normal.

A diffuse reflection still follows the law of reflection; however, because the surface is rough, the normal to the surface will be different at each point, resulting in the reflected rays being scattered.

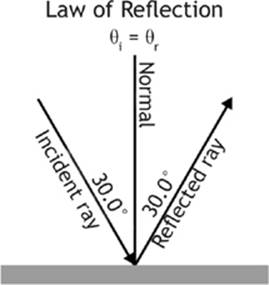
Figure 8.4

The light striking curved mirrors must also follow the law of reflection, but just as with our rough surface, the normal to the mirror will be different at every spot. The resultant reflections off such mirrors are distorted in ways that depend on a number of factors, such as the focal length of the mirror and the distance of the object from the mirror.

Two types of curved mirrors that you are likely to study this year are the concave (converging) and convex (diverging) mirrors. Both of these mirrors are curved, but the shiny surface is on the inner curve of a concave mirror and the outer curve of a convex mirror. Looking at the inside of a shiny metal spoon is similar to looking into a concave mirror. Looking at the back of a shiny metal spoon is similar to looking at a convex mirror. Concave, or “converging,” mirrors are used in searchlights because they help focus the rays of light into smaller and, therefore, brighter areas. Convex, or “diverging,” mirrors are used for side-view mirrors and in convenience stores because they reflect light from a wide area, resulting in a larger field of view.

If you imagine the curved mirror as being a slice taken from a large sphere or ball, the center of curvature (C) would represent the center of that sphere. This places the center of curvature in front of a concave mirror, and behind a convex one. The center of curvature is located at a distance that is twice the focal length of a particular mirror.

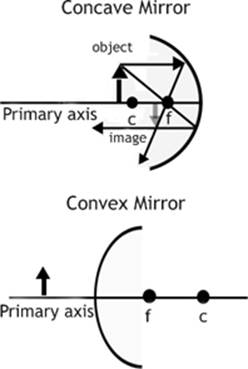
Figure 8.5

Halfway between the center of curvature and the actual vertex, or center of the mirror, lies the focal point (f). Again, this places the focal point for a concave mirror in front, and for a convex mirror, behind. A line drawn through the center of curvature, focal point, and the vertex of the mirror is called the primary axis. For a concave mirror, the focal point represents the point that all light that comes in parallel to the primary axis gets reflected through. For a convex mirror, the focal point is where the reflected light seems to radiate from.

Curved mirrors are capable of producing a variety of images, depending on how far from the mirror the reflected object is placed. Some images are upright, meaning right-side-up. Other images are inverted, or upside-down. Some images are enlarged or bigger, others are reduced or smaller, and still others appear to be the same size as the original object. Some images, which are formed by converging rays of light, are called real images. Other images, formed by diverging rays of light, are called virtual images.

1. When you place an object beyond the center of curvature, the image that is produced will be real, inverted, and smaller than the object.

2. If you place the object at the center of curvature, the image will still be real and inverted, but it will appear to be the same size of the object.

3. If you place the object at a distance that is between the center of curvature and the focal point, the object will be real, inverted, and larger than the object.

4. If you place the object at the focal point, the reflection will appear as a blur. No image is formed. You can use this effect to locate the focal length of a mirror.

5. If you place the object between the focal point and the surface of the mirror, the image will be virtual, upright, and larger than the object.

All images formed by convex mirrors are virtual, upright, and smaller than the object.

Sometimes, drawing a ray diagram, such as the one shown in Figure 8.5, is the most convenient way of determining the type of image that will be formed in a specific situation. However, sometimes you will be asked to find out more specific information, such as the actual distance that the image will be formed from the mirror, the height of the image, or the focal length of the mirror. In such situations, the following equations come in handy.

or

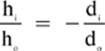
2. Distance Equation →

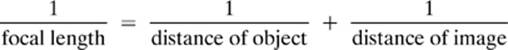
or

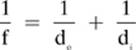
The signs involved with these equations can be somewhat tricky, so you will want to pay attention to the following sign conventions.

Concave (Converging) Mirror

The focal length (f) is always positive.

The distance of the object (d_o) is always positive.

The distance of the image (d_i) is positive for a real image, formed in front of the mirror, and negative for a virtual image, formed behind the mirror.

The height of the image (h_i) will be positive if the image is upright, and negative if it is inverted.

Convex (Diverging) Mirror

The focal length (f) is always negative.

The distance of the object (d_o) is always positive.

The distance of the image (d_i) is always negative, because only a virtual image can be formed by this type of mirror.

The height of the image (h_i) will always be positive, because all images formed by this mirror will be upright.

Example 1

A candle is placed 14.0 cm in front of a concave mirror with a focal length of 10.0 cm. Find the distance from the mirror that the image will be formed.

The first thing that we do is go back and check our sign conventions for concave mirrors, to see if we need to make any of our “givens” negative. The check reveals that for concave mirrors, both of our givens should be positive.

Given: d_o = 14.0 cm f = 10.0 cm

Find: d _i

Checking back to our sign conventions for concave mirrors, we can see that our positive value for the image distance describes a real image, formed in front of the mirror. It will be inverted, because all real images are inverted, and it will be enlarged as well, because it is formed beyond the object.

Example 2

How far away from a convex mirror should an object with a height of 6.0 cm be placed in order to form a virtual image with a height of 4.0 cm at a distance of 2.0 cm behind the mirror?

The question didn”t need to tell us that the image was virtual, because convex mirrors only form virtual images. Checking our sign conventions for convex mirrors, we are reminded that the distance of the image (d_i) formed by these mirrors will always be negative, because they are formed behind the mirror.

Given: h_o = 6.0 cm h_i = 4.0 cm d_i = –2.0 cm

Find: d_o

The positive value of our answer indicates that the object is placed in front of the mirror.

Example 3

A candle with a height of 3.5 cm is placed at a distance of 12.0 cm in front of a concave mirror that has a focal length of 10.0 cm. Find the distance that the image is formed from the mirror and the height of the image.

Checking my sign conventions for a concave mirror, I don”t see anything that needs to be given a negative value.

The negative sign for our second answer indicates that the image is inverted.

Lesson 8–5 Review

1. A _______________ is an image that appears to be formed by diverging rays of light.

2. A lightbulb with a height of 8.5 cm is placed at a distance of 8.0 cm in front of a concave mirror that has a focal length of 14.0 cm. Find the distance that the image is formed from the mirror and the height of the image.

3. A candle with a height of 5.0 cm is placed at a distance of 22.0 cm in front of a convex mirror that has a focal length of 8.0 cm. Find the distance that the image is formed from the mirror and the height of the image.