Homework Helpers: Physics

9 Heat and Thermodynamics

Your study of physics may include a study of the gas laws that you should recall from chemistry. Such overlap is only natural in these sciences, as matter is a concern of both chemists and physicists. Fortunately, if you learned these gas laws well in chemistry class, then a brief review may be all that you need now.

The Kinetic Theory of Gases

The kinetic theory of gases explains the behaviors of gases in terms of their molecules. The theory assumes that:

1. All gases are made up of individual particles (atoms and/or molecules) that are in constant motion. These particles obey Newton”s laws of motion, so they move in random straight lines, unless acted upon by an unbalanced force.

2. All collisions between these particles are considered perfectly elastic, so there is no net loss of momentum or kinetic energy.

As you study the gas laws, you will encounter the term ideal gases. An ideal gas is an imaginary gas with the following characteristics:

1. The particles of an ideal gas are treated as point masses, which means that they are treated as if they take up no space. The entire sample of the gas takes up space, but the space occupied by the individual particles is assumed to be insignificant.

2. The particles of an ideal gas are assumed to exert no attraction on each other.

The model of the ideal gas has been developed to avoid dealing with the unmanageable number of variables involved in real-life samples of gases. Working with “ideal gases” is similar to what you do when you ignore friction in projectile motion problems. Real gas samples can approach ideal conditions, especially when the temperature of the sample is high and the pressure on the sample is low, but they never truly reach the ideal. However, the calculations that we do here are still valid, as your results will closely approximate what you would experience in the real world.

The ideal gas laws are cumulatively concerned with the following characteristics of gas samples:

Pressure (P)—The amount of force exerted per unit of area.

Volume (V) —How much space the gas occupies.

Temperature (T) —The average kinetic energy of the particles of the gas.

Moles (n)—A measure of the amount of particles in the sample, where 1 mole = 6.02 × 10²³ particles.

Molar mass (M)—The mass of one mole of a substance.

Three constants can come into play during gas law calculations:

Universal gas law constant (R)—R = 8.31 J/mol × K

Boltzmann”s constant (k_B)—k_B = 1.38 × 10^–23 J/K

Standard atmospheric pressure (atm) —1 atm = 1.0 × 10⁵ N/m²

Boyle”s Law

First, let”s review Boyle”s law, which shows the relationship between the pressure and volume of an ideal gas

The pressure and volume of a gas at constant temperature are inversely proportional to each other.

P₁ V₁ = P₂ V₂

In physics, pressure is often measured in pascal (Pa), where 1 Pa = 1 N/m². You might also encounter the unit atmosphere (atm): 1 atm = 1.013 × 10⁵ Pa.

Example 1

A 3.50 L sample of hydrogen gas exerts a pressure of 2.00 × 10⁵ Pa at 295 K. If the temperature remains the same, and the gas is allowed to expand to 7.00 L, what pressure will the sample of hydrogen exert?

Given: V₁ = 3.50 L P₁ = 2.00 × 10⁵ Pa V₂ = 7.00 L

Find: P ₂

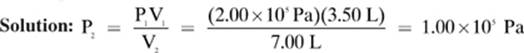
Notice that the volume of the gas was doubled and the pressure exerted by the gas was halved. That is what we meant when we defined Boyle”s law, stating that the pressure and volume of a gas at constant temperature are inversely proportional to each other. As you double one, you halve the other. If you divide one by five, you multiply the other by five. Many questions that you will encounter are designed to test if you understand this relationship between the pressure and volume of an ideal gas.

Example 2

What happens to the volume of an ideal gas at constant temperature if you triple the pressure on it? (Assume the temperature is constant.)

The pressure and volume are inversely proportional to each other. If you triple one, you divide the other variable by three.

Answer: The volume is reduced to one third the original volume.

Charles”s Law

The volume of an ideal gas at constant pressure varies directly with its kelvin temperature.

The important thing to remember when working with Charles”s law is to make sure that you do your calculations in kelvin. The Celsius scale includes zero and negative values, which would result in negative values for volume. This, obviously, wouldn”t make sense, as nothing could be smaller than zero! If the temperature is given to you in Celsius, convert to kelvin as we discussed earlier in this chapter.

Example 3

A sample of neon gas occupies 2.0 L at 22.0°C. How much space would this sample occupy at 68.0°C, assuming the pressure remains constant?

Convert: T₁ = 22.0°C = (22.0 + 273) = 295 K

 T₂ = 68.0°C = (68.0 + 273) = 341 K

Given: T₁ = 295 K T₂ = 341 K V₁ = 2.0 L

Find: V₂

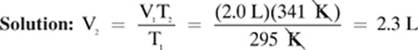
Example 4

A sample of argon gas occupies 352 cm³ at 345 K. At what temperature would this sample of gas occupy 291 cm³? (Assume pressure is constant.)

Given: T₁ = 345 K V₁ = 352 cm³ V₂ = 291 cm³

Find: T₂

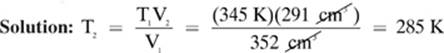
Ideal Gas Law

The ideal gas law shows the relationship between the temperature, volume, and pressure of an ideal gas. There are several versions of the formula that can be derived from one another. I won”t go over the derivations here, but I will go over several examples of problems.

Example 5

How many moles of hydrogen gas would occupy 3.75 dm³ at 42.0°C and 3.00 atm of pressure?

Remember: The units of the constant dictate the units that you must use when solving the problem. Once you realize that you are going to use a formula involving the universal gas constant (R), you should make the necessary conversions to match the units it comes with. Look at the constant and the equivalent units:

R = 8.31 J/mol × K = 8.31 dm³ × kPa/mol × K

= 8.31 (1 × 10^–3 m³) × Pa/mol × K.

It seems to me that, based on our original given units, it makes sense to use the second value for R (8.31 dm³ × kPa/mol × K), as that will result in the least number of conversions.

Example 6

The molecular mass of helium is 4.003 g/mol. How fast do helium molecules in a gas sample with a temperature of 32.0 °C travel?

Lesson 9–4 Review

1. _______________ states that the volume of an ideal gas at constant pressure varies directly with its kelvin temperature.

2. A sample of nitrogen gas occupies 6.65 cm³ at 24.0°C and 2.0 atm of pressure. If the gas is heated to 49.0°C and compressed to a volume of 5.00 cm³, how much pressure would the gas exert in atmospheres?

3. How many molecules of carbon dioxide can be found in a 1.20 m³ sample at a temperature of 25.0° and a pressure of 3.4 × 10⁵ Pa?