SAT Physics Subject Test
Chapter 2 Kinematics
PROJECTILE MOTION
In general, an object that moves near the surface of the earth will not follow a straight-line path; think of a baseball hit by a bat, a golf ball struck by a club, or a tennis ball hit from the baseline. If we launch an object at an angle other than straight upward, and consider only the effect of acceleration due to gravity, then the object will travel along a parabolic trajectory.
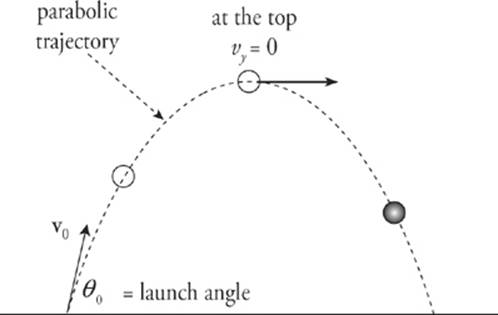
The force of gravity causes an object to fall but does not affect the object”s horizontal motion. To simplify the analysis of parabolic motion, we analyze the horizontal and vertical motions separately, using the Big Five. This is the key to doing projectile motion problems. Calling down the negative direction, we have

The Skinny on Projectile Motion
The perpendicular components of motion (horizontal and vertical) are independent of each other. Work them out separately.
Horizontal
A projectile launched with horizontal velocity (v0x) maintains that velocity. There are no accelerations in the horizontal force, so the x-velocity is constant.
Vertical
The only vertical acceleration is 10 m/s2 downward, so the vy consistently decreases by this magnitude. At the top of the object”s trajectory, vy = 0, and when the object reaches the same height from which it was thrown, vy = –v0y.
The angle of launch determines the relationship of v0y and v0x.
If θ > 45°, then v0y > v0x.
If θ < 45°, then v0y < v0x.
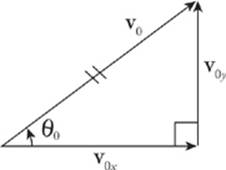
The quantity v0x, which is the horizontal (or x) component of the initial velocity, is equal to v0 cosθ0, where θ0 is the launch angle, the angle that the initial velocity vector, v0, makes with the horizontal. Similarly, the quantity v0y, the vertical (or y) component of the initial velocity, is equal tov0 sinθ0.
![]()
16. An object is thrown horizontally with an initial speed of 10 m/s. How far will it drop in 4 seconds?
Here”s How to Crack It
The first step is to decide whether this is a horizontal question or a vertical question, since you must consider these motions separately. The question “How far will it drop?” is a vertical question, so we”ll use the set of equations listed above under vertical motion. Next, “how far …?” implies that we will use the first of the vertical-motion equations, the one that gives vertical displacement, ∆y.
Free Fall vs.
Horizontal Projection
The time it takes an
object dropped from rest
to fall a certain distance
is the same as if it were
projected horizontally with
any speed.
Since the object is thrown horizontally, there is no vertical component to its initial velocity vector v0; that is, v0y = 0. So
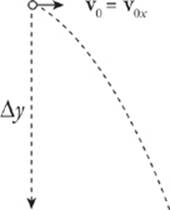
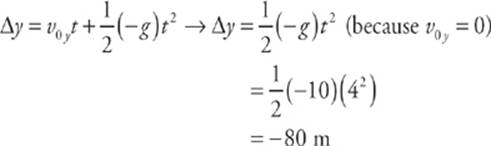
The fact that ∆y is negative means that the displacement is down. Also, notice that the information given about v0x is irrelevant to the question.
![]()
![]()
17. From a height of 100 m, a ball is thrown horizontally with an initial speed of 15 m/s. How far does it travel horizontally in the first 2 seconds?
Here”s How to Crack It
The question “How far does it travel horizontally …?” immediately tells us that we should use the first of the horizontal-motion equations listed on the previous page.
∆x = v0xt = (15 m/s)(2 s) = 30 m
The information that the initial vertical position is 100 m above the ground is irrelevant (except for the fact that it”s high enough that the ball won”t strike the ground before the 2 seconds have elapsed).
![]()
![]()
18. A projectile is traveling in a parabolic path for a total of 6 seconds. How does its horizontal velocity 1 s after launch compare to its horizontal velocity 4 s after launch?
Here”s How to Crack It
The only acceleration experienced by the projectile is due to gravity, which is purely vertical, so there”s no horizontal acceleration. If there”s no horizontal acceleration, then the horizontal velocity cannot change during flight, and the projectile”s horizontal velocity 1 s after it”s launched is the same as its horizontal velocity 3 s later.
No Horizontal Change
Once a projectile is
launched, its horizontal
velocity remains constant
during the entire flight.
![]()
![]()
19. An object is projected upward with a 30° launch angle and an initial speed of 60 m/s. How many seconds will it be in the air? How far will it travel horizontally?
Here”s How to Crack It
The total time the object spends in the air is equal to twice the time required to reach the top of the trajectory (because the parabola is symmetrical). So, as we did in the previous example, we can find the time required to reach the top by setting vy equal to 0, and then double that amount of time:
![]()
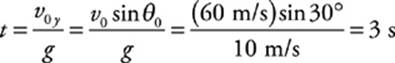
Therefore, the total flight time (that is, up and down) is T = 2t = 2 × (3 s) = 6 s.
Now, using the first horizontal-motion equation, we can calculate the horizontal displacement after 6 seconds.
∆x = v0x T = vo cosθo)T = [(60 m/s) cos 30°](6 s) = 310 m
By the way, the full horizontal displacement of a projectile is called the projectile”s range.
![]()