SAT Physics Subject Test
Chapter 5 Linear Momentum
COLLISIONS
Conservation of linear momentum is routinely used to analyze collisions. Although the objects involved in a collision exert forces on each other during the impact, these forces are only internal (they occur within the system), and the system”s total linear momentum is conserved.
The Skinny on Collisions
Elastic Collision: In an isolated system, momentum and kinetic energy are conserved.
Inelastic Collision: Momentum is conserved and kinetic energy is NOT conserved.
Perfectly or Totally Inelastic Collision: Momentum is conserved, kinetic energy is NOT conserved, and the objects stick together.
Collisions are classified into two major categories: (1) elastic and (2) inelastic. A collision is said to be elastic if kinetic energy is conserved. Ordinary collisions are never truly elastic because there is always a change in energy due to energy transferred as heat, deformation of the objects, or the sound of the impact. However, if the objects do not deform very much (for example, two billiard balls or a hard glass marble bouncing off a steel plate), then the loss of initial kinetic energy is small enough to be ignored, and the collision can be treated as virtually elastic. Inelasticcollisions, then, are ones in which the total kinetic energy is different after the collision. An extreme example of inelasticism is completely (or perfectly or totally) inelastic. In this case, the objects stick together after the collision and move as one afterward. In all cases of isolated collisions (elastic or not), conservation of linear momentum states that
total pbefore collision = total pafter collision
![]()
8. Two balls roll toward each other. The red ball has a mass of 0.5 kg and a speed of 4 m/s just before impact. The green ball has a mass of 0.3 kg and a speed of 2 m/s. After the head-on collision, the red ball continues forward with a speed of 2 m/s. Find the speed of the green ball after the collision. Was the collision elastic?
Here”s How to Crack It
First remember that momentum is a vector quantity, so the direction of the velocity is crucial. Since the balls roll toward each other, one ball has a positive velocity while the other has a negative velocity. Let”s call the red ball”s velocity before the collision positive; then vred = +4 m/s, andvgreen = –2 m/s. Using a prime (´) to denote after the collision, conservation of linear momentum gives us the following:
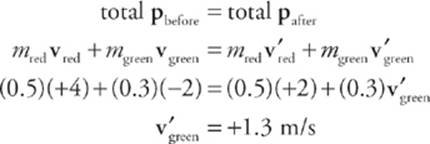
Notice that the green ball”s velocity was reversed (from – to +) as a result of the collision; this typically happens when a lighter object collides with a heavier object. To see whether the collision was elastic, we need to compare the total kinetic energies before and after the collision. In this case, however, we don”t need to do a complicated calculation, since both objects experienced a decrease in speed as a result of the collision. Kinetic energy was lost, so the collision was inelastic; this is usually the case with collisions between ordinary size objects. Most of the lost energy was transferred as heat; the two objects are both slightly warmer as a result of the collision.
![]()
![]()
9. Two balls roll toward each other. The red ball has a mass of 0.5 kg and a speed of 4 m/s just before impact. The green ball has a mass of 0.3 kg and a speed of 2 m/s. If the collision is perfectly inelastic, determine the velocity of the composite object after the collision.
Here”s How to Crack It
If the collision is perfectly inelastic, then, by definition, the masses stick together after impact, moving with a velocity, v. Applying conservation of linear momentum, we find
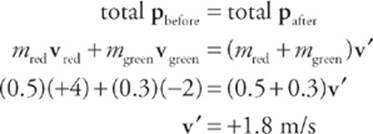
![]()
![]()
Questions 10-11
A block of mass M = 4 kg is moving with velocity V = 6 m/s toward a target block of mass m = 2 kg, which is stationary (v = 0). The objects collide head-on, and immediately after the collision, the speed of block m is 4 times the speed of block M.
10. What is the speed of block M after the collision?
11. Is the collision elastic?
Here”s How to Crack It
10. If we let V´ be the speed of block M immediately after the collision, then the speed of block m will be 4V´. By applying conservation of linear momentum, we find that
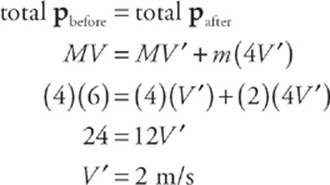
Therefore, the speed of block M immediately after the collision is 2 m/s (and the speed of block m immediately after the collision is 8 m/s).
11. A collision is elastic if the total kinetic energy is conserved. Since
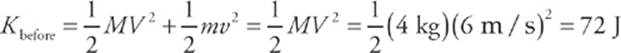
and
![]()
Kbefore = Kafter, so the collision is elastic.
![]()
In the case of two dimensional collisions (e.g. two cars colliding at an intersection or two billiard balls colliding and moving off at angles), remember that there are two conservation of momentum equations.
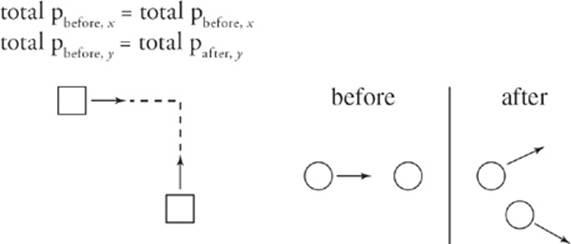
Examples of Two-Dimensional Collisions