SAT Physics Subject Test
Chapter 6 Curved and Rotational Motion
TORQUE
Torque is the quantity that measures how effectively a force causes rotation. Consider a uniform rod that pivots around one of its ends. For simplicity, let”s assume that the rod is at rest. What effect, if any, would each of the four forces in the figure below have on the potential rotation of the rod?
The Skinny on Torque
Torque isn”t actually a force, but it acts like one. Think of torque as a turning force; it causes objects to rotate either in a clockwise or counterclockwise direction.
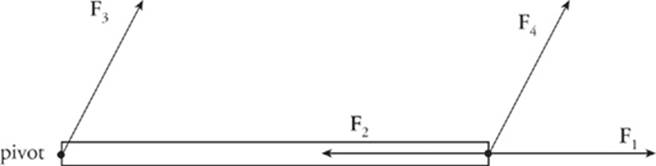
Our intuition tells us that F1, F2, and F3 would not cause the rod to rotate, but F4 would. What”s different about F4? It has torque. Just like a force is a vector quantity that produces linear acceleration, a torque is a vector quantity that produces angular acceleration. A torque can be thought of as positive if it produces a counterclockwise rotation and negative if it produces a clockwise rotation. To find the net torque acting on an object, simply sum the torques exactly as you would forces.
The torque of a force can be defined as follows. Let r be the distance from the pivot (axis of rotation) to the point of application of the force F, and let θ be the angle between vectors r and F.
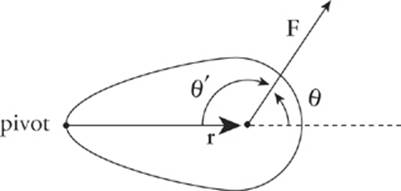
Then the magnitude of the torque of F, denoted by τ(tau), is defined as
τ = rF sin θ.
In the previous figure, the angle between the vectors r and F is θ. Imagine sliding r over so that its initial point is the same as that of F.
The angle between two vectors is the angle between them when they start at the same point.
However, we can use the supplementary angle θ” in place of θ in the definition of torque. This is because torque depends on sin θ, and the sine of an angle and the sine of its supplement are always equal. Therefore, when figuring out torque, use whichever of these angles is most convenient.
Let”s see if this mathematical definition of torque proves what we suspected about forces F1, F2, F3, and F4.
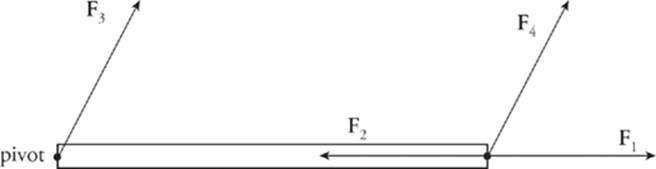
The angle between r and F1 is 0, and θ = 0 tells us that sin θ = 0, so by the definition of torque, τ = 0 as well. The angle between r and F2 is 180°, and θ = 180° gives us sin θ = 0, so τ = 0. For F3, r = 0 (because F3 acts at the pivot, so the distance from the pivot to the point of application ofF3 is zero); since r = 0, the torque is 0 as well. However, for F4, neither r nor sin θ is zero, so F4 has a nonzero torque. Of the four forces shown in that figure, only F4 has torque and would produce rotational acceleration.
There”s another way to determine the value of the torque. Of course, it gives the same result as the method given above, but this method is often easier to use. Look at the same object and force.
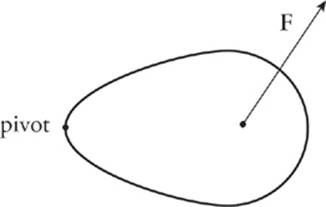
Instead of determining the distance from the pivot point to the point of application of the force, we will now determine the (perpendicular) distance from the pivot point to what”s called the line of action of the force. This distance is the lever arm (or moment arm) of the force F relative to the pivot and is symbolized by l.
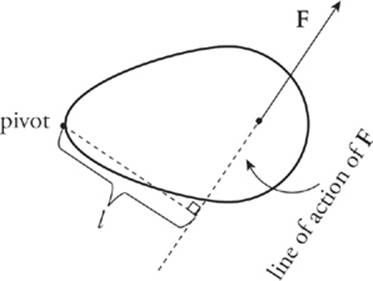
The torque of F is defined as the product
τ = lF
(Just as the lever arm is sometimes called the moment arm, the torque is also called the moment of the force.) The fact that these two definitions of torque, τ = rFsin θ and τ = lF, are equivalent follows from the fact that l = r sin θ.
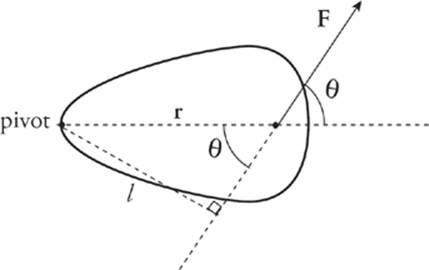
Since l is the component of r that”s perpendicular to F, it is also symbolized by r⊥ (“r perp”). So the definition of torque can be written as τ = r⊥F.
These two equivalent definitions of torque make it clear that only the component of F that”s perpendicular to r produces torque. The component of F that”s parallel to r does not produce torque. Notice that τ = rFsin θ = rF⊥, where F⊥ (“F perp”) is the component of F that”s perpendicular tor.
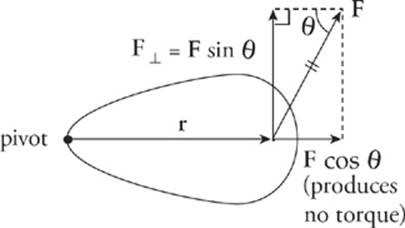
So the definition of torque can also be written as τ = rF⊥.
![]()
9. A student pulls down with a force of 40 N on a rope that winds around a pulley of radius 5 cm.
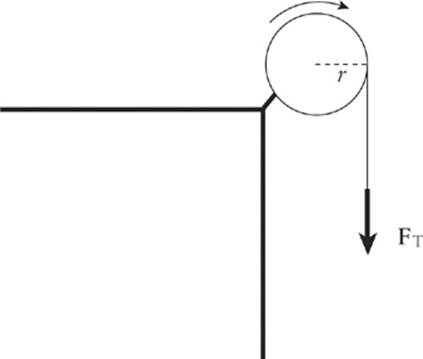
What”s the torque of this force?
Here”s How to Crack It
Since the tension force, FT, is tangent to the pulley, it is perpendicular to the radius vector r at the point of contact.
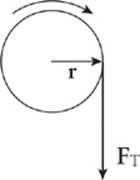
Therefore, the torque produced by this tension force is
τ = rFT = (0.05 m)(40 N) = 2 N × m
![]()
![]()
10. The cylinder below is free to rotate around its center. What is the net torque on the cylinder?
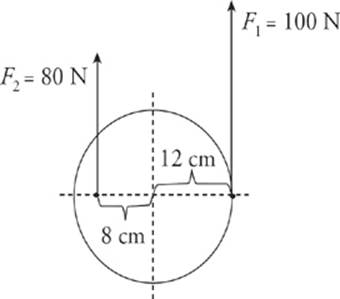
Here”s How to Crack It
Each of the two forces produces a torque, but these torques oppose each other. The torque of F1 is counterclockwise, and the torque of F2 is clockwise.
The net torque is the sum of all the torques. Counting a counterclockwise torque as positive and a clockwise torque as negative, we have
τ1 = +r1F1 = +(0.12 m)(100 N) = +12 N × m
and
τ2 = –r2F2 = –(0.08 m)(80 N) = –6.4 N × m
so
τnet = Σ τ = τ1 + τ2 = (+12 N·m) + (–6.4 N·m) = +5.6 N × m
![]()