SAT Physics Subject Test

Chapter 2 Kinematics

SPEED AND VELOCITY

When we”re in a moving car, the speedometer tells us how fast we”re going; it gives us our speed. But what does it mean to have a speed of, say, 10 m/s? It means that we”re covering a distance of 10 meters every second. What if the car changes its speed as it drives (say, it stops at a traffic light)? We can look at a quantity that gives us information about the entire trip. By definition, average speed is the ratio of the total distance traveled to the time required to cover that distance.

average speed =

The car”s speedometer doesn”t care in what direction the car is moving. You could be driving north, south, east, or west, the speedometer would make no distinction: 55 miles per hour, north and 55 miles per hour, east register the same on the speedometer as 55 miles per hour. Speed is a scalar quantity.

However, we also need to include direction in our descriptions of motion. We just learned about displacement, which takes both distance (net distance) and direction traveled into account. The vector that embodies both speed and direction is called velocity, symbolized v, and the definition of average velocity is:

average velocity =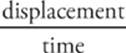

(The bar over the v means average.) Because ∆s is a vector, is also a vector, and because ∆t is a positive scalar, the direction of v is the same as the direction of ∆s. The magnitude of the velocity vector is called the object”s speed and is expressed in units of meters per second (m/s).

The Skinny on Velocity

Since velocity is defined as the change in position per second, we can say the following (for motion along the x- or y-axis):

If v is positive, then the displacement is positive: The object is traveling in a positive direction.

If v is negative, then the displacement is negative: The object is traveling in a negative direction.

If v = 0, then the displacement is zero: The object is motionless.

Notice the distinction between speed and velocity. In everyday language, they”re often used interchangeably. However, in physics, speed and velocity are technical terms with different definitions.

Speed has no direction and is always taken as a positive.

Velocity is speed and direction.

The magnitude of the average velocity is not called the average speed. Average speed is the total distance traveled divided by the elapsed time. Average velocity is the net distance traveled divided by the elapsed time.

Average Velocity vs. Average Speed

Average speed is not the magnitude of the average velocity unless the object has moved in a straight line.

3. Assume that the runner in sample question 3 completes the race in 1 minute and 20 seconds. Find her average speed and the magnitude of her average velocity.

Here”s How to Crack It

Average speed is total distance divided by elapsed time. Since the length of the track is 500 m, the runner”s average speed was (500 m)/(80 s) = 6.3 m/s. However, since her displacement was zero, her average velocity was zero also: v = ∆s/∆t = (0 m)/(80 s) = 0 m/s.

4. Is it possible to move with constant speed but not constant velocity? Is it possible to move with constant velocity but not constant speed?

Here”s How to Crack It

The answer to the first question is yes. For example, if you set your car”s cruise control at 55 miles per hour but turn the steering wheel to follow a curved section of road, then the direction of your velocity changes (which means your velocity is not constant), even though your speed doesn”t change.

The answer to the second question is no. Velocity means speed and direction; if the velocity is constant, then that means both speed and direction are constant. If speed were to change, then the velocity vector”s magnitude would change (by definition), which immediately implies that the vector changes.