SAT Physics Subject Test
Chapter 8 Electric Forces and Fields
THE ELECTRIC FIELD
Objects on Earth (and those in orbit) experience a gravitational force directed toward the earth”s center. For objects located outside the earth, this force varies inversely with the square of the distance and directly with the mass of the gravitational source. A vector diagram of the gravitational field surrounding the earth looks like the following:
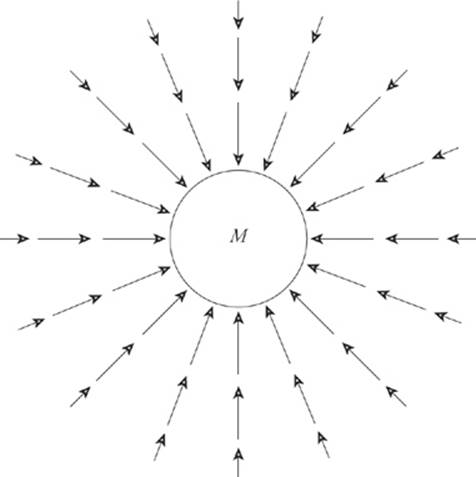
We can think of the space surrounding the earth as permeated by a gravitational field that”s created by the earth. Any mass that”s placed in this field experiences a gravitational force due to this field.
The same process is used to describe the electric force. Rather than having two charges reach out across empty space to each other to produce a force, we can instead interpret the interaction in the following way: The presence of a charge creates an electric field in the space that surrounds it. Another charge placed in the electric field created by the first charge will experience a force due to the field.
Consider a point charge Q in a fixed position and assume that it”s positive. Now imagine moving a tiny positive test charge q around to various locations near Q. At each location, measure the force that the test charge experiences, and call it Fon q. Divide this force by the test charge q; the resulting vector is the electric field vector, E, at that location.
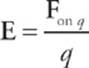
The reason for dividing by the test charge is simple. If we were to use a different test charge with, say, twice the charge of the first one, then each of the forces F we”d measure would be twice as much as before. But when we divided this new, stronger force by the new, greater test charge, the factors of 2 would cancel, leaving the same ratio as before. So this ratio tells us the intrinsic strength of the field is due to the source charge, independent of whatever test charge we may use to measure it.
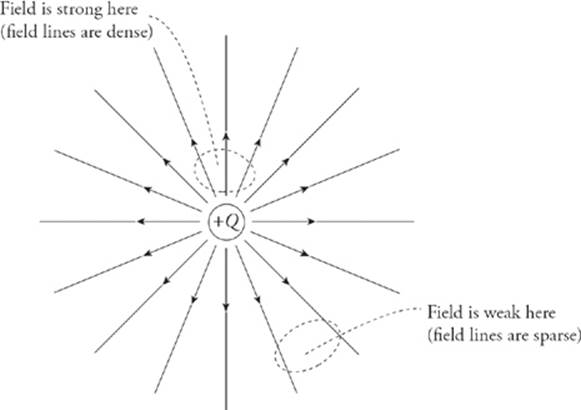
What would the electric field of a positive charge Q look like? Since the test charge is always assigned to be positive in electrostatics, every electric field vector would point radially away from the source charge. If the source charge is positive, the electric field vectors point away from it; if the source charge is negative, then the field vectors point toward it. Since the force decreases as we get farther away from the charge (as 1/r2), so does the electric field. This is why the electric field vectors farther from the source charge are shorter than those that are closer.
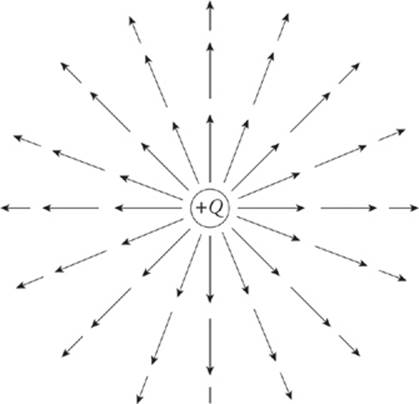
Since the force on the test charge q has a strength of kqQ/r2, when we divide this by q, we get the expression for the strength of the electric field created by a point-charge source of magnitude Q.
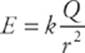
To make it easier to sketch an electric field, we can draw lines through the vectors such that the electric field vector is tangent to the line everywhere it”s drawn.
Now, your first thought might be that obliterating the individual field vectors deprives us of information, since the length of the field vectors told us how strong the field was. Well, although the individual field vectors are gone, the strength of the field can be figured out by looking at the density of the field lines. Where the field lines are denser, the field is stronger.
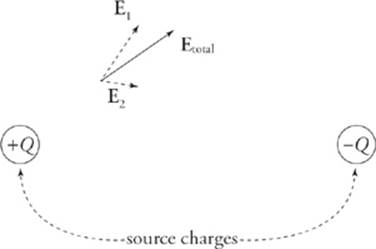
Electric field vectors can be added like any other vectors. If we had two source charges, their fields would overlap and effectively add; a third charge wandering by would feel the effect of the combined field. At each position in space, add the electric field vector due to one of the charges to the electric field vector due to the other charge: Etotal = E1 + E2. (This is superposition again.) In the diagram below, E1 is the electric field vector at a particular location due to the charge +Q, and E2 is the electric field vector at that same location due to the other charge, –Q. Adding these vectors gives the overall field vector Etotal at that location.
If this is done at enough locations, we can sketch the electric field lines.
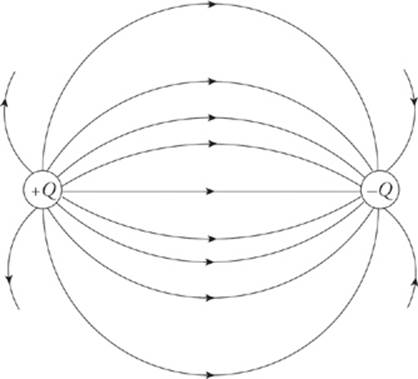
Notice that, as with electric field vectors, electric field lines always point away from positive source charges and toward negative ones. Two equal but opposite charges, like the ones shown in the diagram above, form a pair called an electric dipole.
If a positive charge +q were placed in the electric field above, it would experience a force that is tangent to, and in the same direction as, the field line passing through +q”s location. After all, electric fields are sketched from the point of view of what a positive test charge would do. However, if a negative charge –q were placed in the electric field, it would experience a force that is tangent to, but in the direction opposite from, the field line passing through –q”s location.
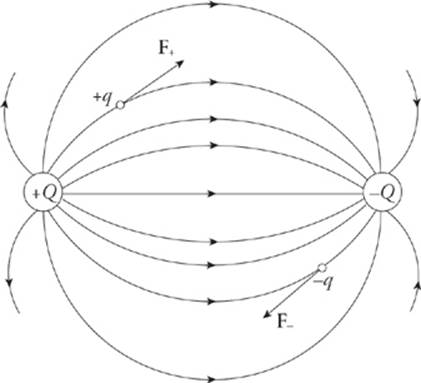
Finally, notice that electric field lines never cross.
![]()
4. A charge q = +3.0 nC is placed at a location at which the electric field strength is 400 N/C. Find the force felt by the charge q.
Here”s How to Crack It
From the definition of the electric field, we have the following equation:
Fon q = qE
Therefore, in this case, Fon q = qE = (3 × 10–9 C)(400 N/C) = 1.2 10–6 N.
![]()
![]()
5. A dipole is formed by two point charges, each of magnitude 4.0 nC, separated by a distance of 6.0 cm. What is the strength of the electric field at the point midway between them?
Here”s How to Crack It
Let the two source charges be denoted +Q and –Q. At Point P, the electric field vector due to +Q would point directly away from +Q, and the electric field vector due to –Q would point directly toward –Q. Therefore, these two vectors point in the same direction (from +Q to –Q), so their magnitudes would add.
The Skinny on the Electric Field
For an Electric Field produced by a charge, it points away from positives and toward negatives.
A charge feeling a force due to an existing ![]() will want to move in the direction of
will want to move in the direction of ![]() if it is positive and opposite
if it is positive and opposite ![]() if it is negative.
if it is negative.
Using the equation for the electric field strength due to a single point charge, we find that
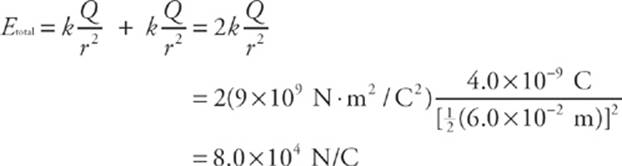
![]()
![]()
6. If a charge q = –5.0 pC were placed at the midway point described in the previous example, describe the force it would feel. (“p” is the abbreviation for “pico-,” which means 10–12.)
Here”s How to Crack It
Since the field E at this location is known, the force felt by q is easy to calculate.
Fon q = qE = (–5.0 × 10–12 C)(8.0 × 104 N/C to the right) = 4.0 × 10–7 N to the left.
![]()
![]()
7. What can you say about the electric force that a charge would feel if it were placed at a location at which the electric field was zero?
Here”s How to Crack It
Remember that Fon q = qE. So if E = 0, then Fon q = 0. (Zero field means zero force.)
![]()