SAT Physics Subject Test
Chapter 13 Waves
Waves make up approximately 20 percent of the SAT Physics Subject Test. But what are they, exactly? Imagine holding the end of a long rope in your hand, with the other end attached to a wall. Move your hand up and down, and you”ll create a wave that travels along the rope, from your hand to the wall. This is the basic idea of a mechanical wave: a disturbance transmitted by a medium from one point to another, without the medium itself being transported. In the case of water waves, wind or an earthquake can cause a disturbance in the ocean, and the resulting waves can travel thousands of miles. No water actually makes that journey; the water is only the medium that conducts the disturbance.
TRANSVERSE TRAVELING WAVES
Let”s return to our long rope. Someone standing near the system would see peaks and valleys actually moving along the rope, in what”s called a traveling wave.
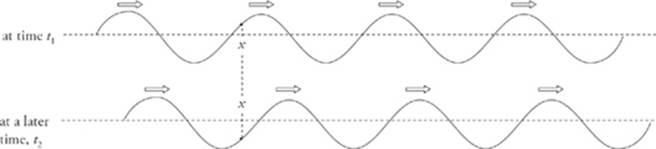
At any point (x) along the rope, the rope has a certain, and varying, vertical displacement. It”s this variation in the vertical displacement that defines the shape of the wave. In the figure above, one particular location along the rope—marked x—is shown. Notice that, at time t1, the vertical position y of the rope at x is slightly positive (it”s above the horizontal). But at a later time, t2, the vertical position of the rope at this same x is slightly negative (it”s below the horizontal). It”s clear that for a traveling wave, the displacement y of each point depends not only on x but also on t. An equation that gives y must therefore be a function of both position (x) and time (t). Because y depends on two independent variables, wave analysis can be difficult. But there”s a way of looking at waves that simplifies things.
Instead of looking at a wave in which both variables (x and t) are changing, we”ll allow only one of the variables to change. We”ll use two points of view.
Point of View #1: x varies, t does not
Point of View #2: t varies, x does not
Point of View #1: x Varies, t Does Not
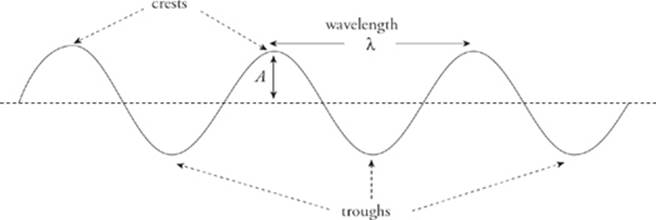
To keep t from varying, we must freeze time. How do we do this? By imagining a photograph of the wave. In fact, the figure above shows two snapshots: one taken at time t1 and the second taken at a slightly later time, t2. All the x”s along the rope are visible (that is, x varies), but t does not. What features of the wave can we see in this point of view? Well, we can see the points at which the rope has its maximum vertical displacement above the horizontal; these points are called crests. The points at which the rope has its maximum vertical displacement below the horizontal are called troughs. These crests and troughs repeat themselves at regular intervals along the rope, and the distance between two adjacent crests (or two adjacent troughs) is the length of one wave, and is called the wavelength (λ, lambda). Also, the maximum displacement from the horizontalequilibrium position of the rope is known as the amplitude (A) of the wave. Be careful: A is just the distance from the “middle” to a crest, not from a trough to a crest.
Point of View #2: t Varies, x Does Not
Now we will designate one position x along the rope to watch as time varies. One way to do this is to visualize two screens in front of the rope, with only a narrow gap between them. We can then observe how a single point on the rope varies as a wave travels behind the screen (the wave is traveling because we aren”t freezing time here). This point on the rope moves up and down. Since the direction in which the rope oscillates (vertically) is perpendicular to the direction in which the wave propagates (or travels, horizontally), this wave is transverse. The time it takes for one complete vertical oscillation of a point on the rope is called the period, T, of the wave, and the number of cycles it completes in one second is called its frequency, f. The period and frequency are established by the source of the wave and T = 1/f.
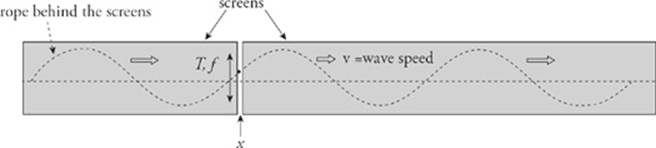
Four of the most important characteristics of any wave are its wavelength, amplitude, period, and frequency.
A fifth important characteristic of a traveling wave is its speed, v. Look at the figure above and imagine the visible point on the rope moving from its crest position, down to its trough position, and then back up to the crest position. How long did this take? The period, T. Behind the screen, the wave moved a distance of one wavelength. T is the time required for one wave to travel by a point, and is the distance traveled by one wave. Therefore, the equation distance = rate × time becomes
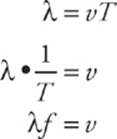
The simple equation v = λf shows how the wave speed, wavelength, and frequency are interconnected. It”s the most basic equation in wave theory—know it for the test.
![]()
1. A traveling wave on a rope has a frequency of 2.5 Hz. If the speed of the wave is 1.5 m/s, what are its period and wavelength?
Here”s How to Crack It
The period is the reciprocal of the frequency.
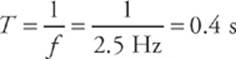
The wavelength can be found from the equation λf = v.
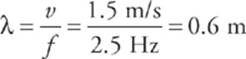
![]()
![]()
2. The period of a traveling wave is 0.5 s, its amplitude is 10 cm, and its wavelength is 0.4 m. What are its frequency and wave speed?
Here”s How to Crack It
The frequency is the reciprocal of the period: f = 1/T = 1/(0.5 s) = 2 Hz. The wave speed can be found from the equation v = λf.
v = λf = (0.4 m)(2 Hz) = 0.8 m/s
(Notice that the frequency, period, wavelength, and wave speed have nothing to do with the amplitude.)
![]()
Don”t be fooled by this formula. The speed of a wave does not depend on the frequency or wavelength. It depends on properties of the medium.
Wave Rule #1: All waves of the same type in the same medium have the same speed.
If you move a rope up and down at a certain frequency and then suddenly increase that frequency, the speed remains unchanged. The wavelength, therefore, decreases. This makes sense since you are creating more pulses per second, each pulse won”t have as much time to move down the rope before the next pulse is created. The pulses are closer together, meaning the wavelength has decreased.
Wave Speed on a Stretched String
We can also derive an equation for the speed of a transverse wave on a stretched string or rope. Let the mass of the string be m and its length be L; then its linear mass density (μ) is m/L. If the tension in the string is FT, then the speed of a traveling transverse wave on this string is given by
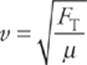
Notice that v depends only on the physical characteristics of the string—its tension and linear density. So, because v = λf for a given stretched string, varying f will create different waves that have different wavelengths, but v will not vary.
![]()
Questions 3-4
A horizontal rope with linear mass density µ = 0.5 kg/m has a tension of 50 N. The non-attached end is oscillated vertically with a frequency of 2 Hz.
3. What are the speed and wavelength of the resulting wave?
4. How would you answer these questions if f were increased to 5 Hz?
Here”s How to Crack It
3. Wave speed is established by the physical characteristics of the rope.

With v, we can find the wavelength: λ = v/f = (10 m/s)/(2 Hz) = 5 m.
4. If f were increased to 5 Hz, then v would not change, but λ would; the new wavelength would be
λ′ = v / f′ = (10) m/s)/ (5 Hz) = 2 m
![]()
Wave Rule #2: When a wave passes into a new medium, its frequency stays the same.
This can be understood if we represent a wave as a series of wavefronts—lines that represent, say, the crests.
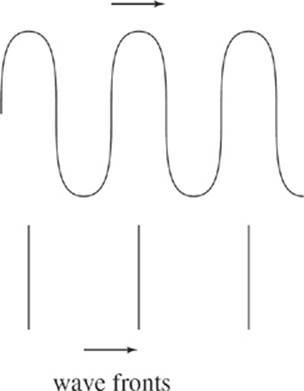
If a wave moves into a new medium, its speed will most likely change. However, the number of wave fronts that approach the boundary per second must be equal to the number of wavefronts that leave the boundary (that is, rate in equals rate out). The number of wave fronts per second is the frequency.
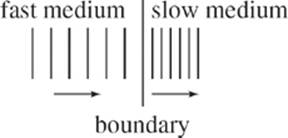
While the number of wavefronts leaving the first medium per second equals the number entering the second medium per second, their spacing (wavelength) changes.
![]()
5. Two ropes of unequal linear densities are connected, and a wave is created in the rope on the left, which propagates to the right, toward the interface with the heavier rope.
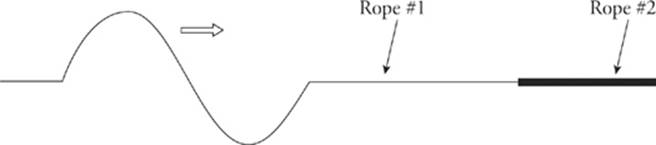
When a wave strikes the boundary to a new medium (in this case, the heavier rope), some of the wave”s energy is reflected and some is transmitted. How do the speed and wavelength of the incident wave compare with the speed and wavelength of the transmitted wave?
Here”s How to Crack It
Since the wave enters a new medium, it will have a new wave speed. Because rope #2 has a greater linear mass density than rope #1, and because v is inversely proportional to the square root of the linear mass density, the speed of the wave in rope #2 will be less than the speed of the wave in rope #1. Since v = λf, and f does not change the fact that v changes means that λ must change too. In particular, since v decreases upon entering rope #2, so will λ.
![]()