SAT Subject Test Physics (2012)
PART III. PHYSICS TOPIC REVIEW
Chapter 15. WAVES
You may already be familiar with how to form water waves or waves on a rope, but being comfortable describing the properties of waves and the interactions between them will help you answer several questions on SAT Physics. In this chapter, you will focus on waves that disturb materials, such as ropes, water, and air. In the following chapter, you will review light waves and similar types of waves.
Wave Motion
Drop a pebble into a lake, and you will observe ripples extending outward in all directions. The ripples are produced because a disturbance is transmitted away from the source. The disturbance is the wave, and it carries energy from one location to another.
A water wave is an example of a mechanical wave, which is a traveling disturbance that requires a medium through which to travel. A medium is a material through which a wave moves. In the case of a water wave, the medium is water. As the wave travels through the medium, the particles of the medium are disturbed and vibrate back and forth. Once the wave passes a given point, the particles return to their normal resting positions.
Not all waves require a medium. Electromagnetic Waves are made up of electric and magnetic fields and do not require a medium. Light, microwaves, and ultraviolet radiation are electromagnetic waves. These kinds of waves will be discussed in the next chapter.
Transverse and Longitudinal Waves
Waves can be further classified as transverse or longitudinal. A transverse wave causes the particles of the medium to vibrate perpendicular to the direction of motion of the wave. A longitudinal wave causes the particles of the medium to vibrate parallel to the direction of motion of the wave.
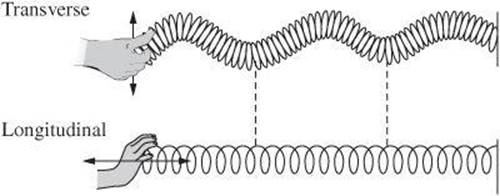
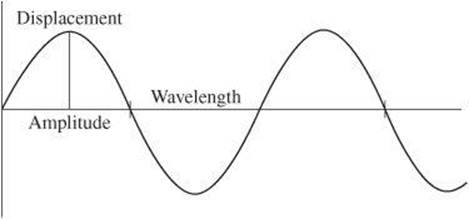
Both kinds of waves can be described by several basic properties. It is often convenient to represent a wave as a graph similar to the following diagram. As you can see, the maximum displacement of the particles of the medium leads to high points and low points. For a transverse wave, the high points are also known as crests and the low points as troughs. For a longitudinal wave, the high points relate to regions where particles of the medium are most crowded and the low points to regions where the particles are most spread out. The crowded regions are known as compressions and the expanded regions as rarefactions.
The maximum displacement of the particles of a medium describes the amplitude of a wave. The distance between similar points on consecutive waves is the wavelength of the wave, λ. For example, one wavelength might be measured from crest to crest, trough to trough, or two other similar points.
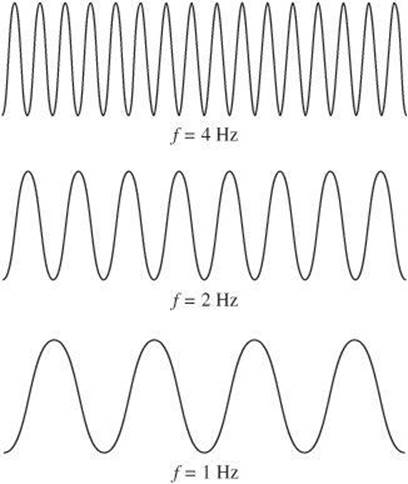
The frequency of a wave, f, describes the number of waves that pass a given point per second. Notice that the waves in the following diagram all have the same amplitude, but different frequencies and wavelengths. At a given speed, frequency and wavelength are inversely proportional, so the wave with the greatest wavelength has the smallest frequency and the wave with the smallest wavelength has the greatest frequency.
The speed of a wave equals the product of the frequency of a wave and its wavelength. This relationship is summarized by the following equation.
![]()
Example:
A wave produced by a musical instrument travels at a speed of 200 m/s and has a frequency of 440 Hz. What is the wavelength of the wave?

Resonance
All objects have a natural frequency or group of frequencies at which they vibrate. The natural frequency depends on the physical properties of the object, including its mass, shape, and elasticity. However, an object may be set into vibration if an external force is applied to it. The resulting vibration is known as a forced vibration. The amplitude of the forced vibration depends on the difference between the applied frequency f and the natural frequency fo. It is at a maximum when the applied frequency equals the natural frequency, ![]() . The effect of the maximum is known as resonance, and the natural frequency is therefore known as the resonant frequency. In other words, if the frequency of forced vibrations matches the natural frequency of an object, there is a dramatic increase in the amplitude of the result wave.
. The effect of the maximum is known as resonance, and the natural frequency is therefore known as the resonant frequency. In other words, if the frequency of forced vibrations matches the natural frequency of an object, there is a dramatic increase in the amplitude of the result wave.
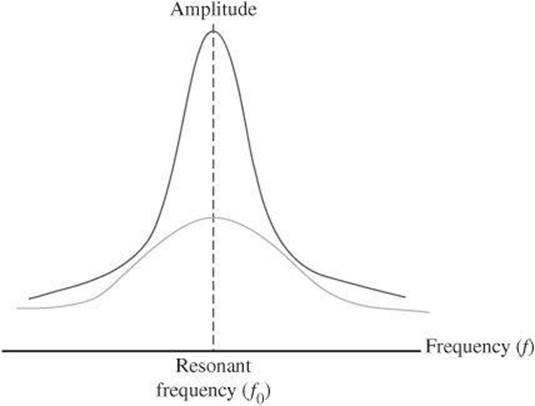
A common example used to describe this phenomenon is a simple child’s swing. The swing, like other objects, has a natural frequency. If you exert a force on a swing by pushing, your timing determines the resulting effect. Even a small force can result in a large amplitude if delivered along with the natural frequency of the swing.
Interference
Two waves traveling in the same medium at the same time experience interference. Constructive interference occurs when two waves combine in such a way that the amplitude of the resulting wave is greater than either of the two individual waves. Waves that interfere constructively are said to be in phase. Once the waves pass one another, they retain their original properties. Destructive interference occurs when two waves combine in such a way that the amplitude of the resulting wave is less than either of the two individual waves. Again, the waves retain their original properties after they pass one another. The rule that describes the interference of waves is known as the law of superposition.
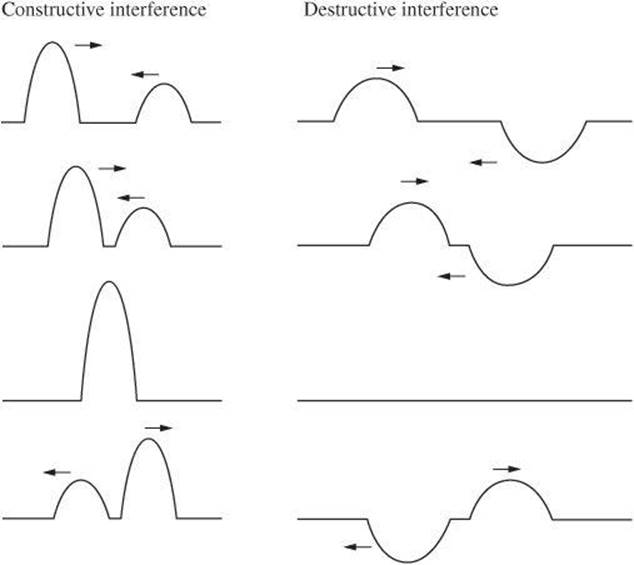
Standing Waves
When two waves of the same frequency traveling in opposite directions in the same medium interfere, a standing wave can be produced. In a standing wave, fixed points called nodes that experience no net displacement are formed. The nodes are the result of destructive interference. Because the nodes remain in the same positions in the medium, the wave appears to be standing still.
The point directly between two nodes experiences the maximum amount of displacement. These points are called antinodes, and they result from constructive interference. The pattern of nodes and antinodes depends on the frequency of the waves.
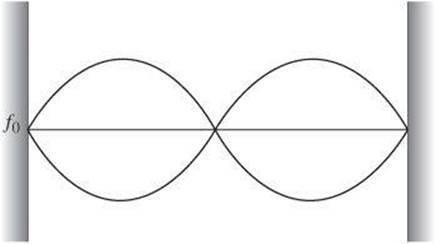
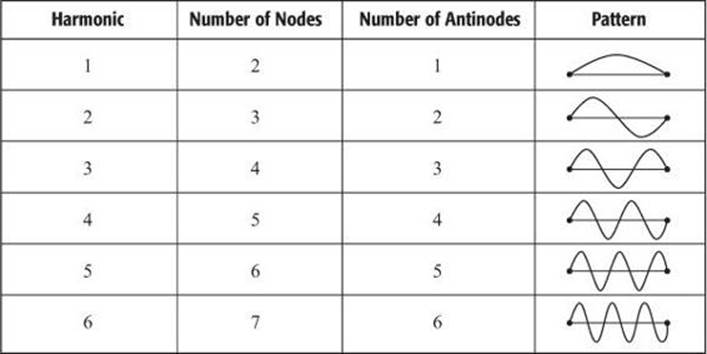
The natural frequencies are often described as the harmonics of an object or system. The first harmonic is the standing wave with two nodes and one antinode. It has the longest wavelength and the lowest frequency. The lowest frequency is also known as the fundamental frequency. All other harmonics are whole number multiples of the fundamental frequency. Each additional harmonic adds one node and antinode.
Sound Waves
When you hear a sound, you are receiving a longitudinal mechanical wave. Unlike light, which is an electromagnetic wave, sound cannot travel through the vacuum of space. Instead, it requires a medium through which to travel. The following diagram relates to the compressions and rarefactions of the medium with the properties of the wave.
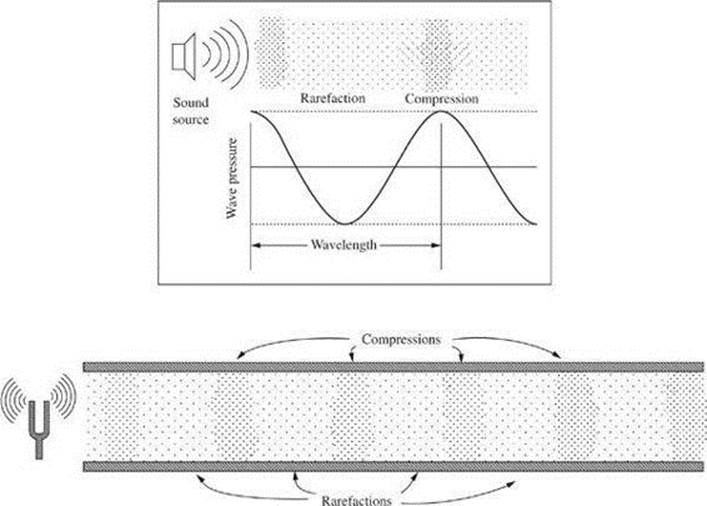
A sound is produced when an object vibrates. Any vibrating object produces a sound, even if you cannot hear it. The frequencies of sound waves are classified as audible if they are within the range of human hearing. This range is describes as between 20 and 20,000 Hz. Sound waves are considered infrasonic if they are below 20 Hz and ultrasonic if they are above 20,000 Hz.
The frequency of a sound wave determines a property known as pitch. The pitch of a sound describes how high or how low the sound is. A sound with a high frequency, such as that produced by a flute, has a high pitch. A sound with a low frequency, such as that produced by a tuba, has a low pitch.
The frequencies of sound can be used to distinguish music from noise. While noise generally consists of a mixture of frequencies with no discernable relationship, music consists of frequencies with an obvious mathematical relationship. Two waves with a whole number ratio between their frequencies interfere to form a wave with a repeating pattern described as music. For example, suppose two waves—for which their frequencies are in a ratio of 2:1—interfere. The resulting wave has a regular, repeating pattern known as an octave.
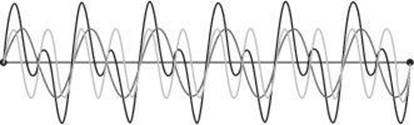
Periodic, repeating fluctuations in the intensity of a sound that result when two waves with slightly different frequencies interfere are known as beats. The beat frequency is equal to the difference in frequency of the two notes that produce the beats through interference.
Example:
Two sounds occur at the same time. One sound has a frequency of 248 Hz, and the other has a frequency of 250 Hz. What beat frequency do you hear?
![]()
Doppler Effect
A relative change in frequency due to motion of a sound of source or its observer produces the Doppler effect. Consider a police car with a siren moving from left to right as shown in the following diagram. Sound waves are emitted in all directions from the siren. The frequency at which the sound is produced remains constant. However, as sound waves move forward from the car, the car also moves forward. Thus, the sound waves tend to bunch up so the frequency with which they reach an observer increases. The frequency of the waves heard by the observer in front of the car is therefore greater than the source frequency, so the pitch of the siren sounds higher.
Behind the car, the sound waves reach an observer with a lower frequency as the car moves away from the observer. The frequency of the waves heard by the observer in back of the car is, therefore, lower than the source frequency, so the pitch of the siren sounds lower.

Note that the Doppler effect is also observed if the observer moves relative to a stationary source of sound. The Doppler effect is commonly observed with sound waves, but it occurs for all kinds of waves.
Test-Taking Hint
Review the general properties of all waves. Then make sure you know the properties specific to certain kinds of waves. For example, know how the particle motion related to sound waves can be explained. Later on, you will need to know how to explain the properties of electromagnetic waves.
REVIEW QUESTIONS
Select the choice that best answers the question or completes the statement.
1. How does a mechanical wave differ from an electromagnetic wave?
(A) a mechanical wave requires a medium through which to travel.
(B) a mechanical wave can travel through a vacuum.
(C) a mechanical wave produces noise as opposed to music.
(D) a mechanical wave is produced as a result of a forced vibration.
(E) a mechanical wave can experience the Doppler effect.
2. A transverse wave moves to the right in the plane of this paper. In which direction will the particles of the medium vibrate?
![]()
![]()
3. A musical note has a frequency of 440 Hz. What is the wavelength of the sound if it has a speed of 345 m/s?
(A) 0.26 m
(B) 0.78 m
(C) 1.0 m
(D) 1.2 m
(E) 1.5 m
4. A student strikes a tuning fork. How long does it take for the sound to reach the observer? [Use 340 m/s for the speed of sound in air.]
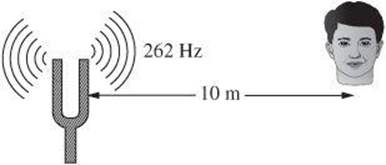
(A) 0.03 s
(B) 0.04 s
(C) 1.3 s
(D) 2.6 s
(E) 3.4 s
5. At which letter do the waves interfere destructively?
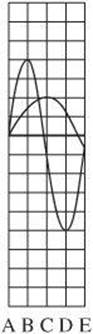
(A) point A
(B) point B
(C) point C
(D) point D
(E) point E
6. How many nodes are present for the wave depicted below?
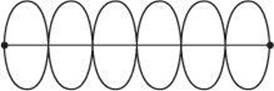
(A) 3
(B) 6
(C) 7
(D) 14
(E) 20
7. A train approaches you as its horn blows. How is the perceived sound of the horn affected by the relative motion between the train and you?
(A) the speed decreases.
(B) the amplitude increases.
(C) the frequency decreases.
(D) the pitch increases.
(E) the direction of the sound shifts.
Questions 8–10 relate to the diagram below, which shows the representation of a wave.
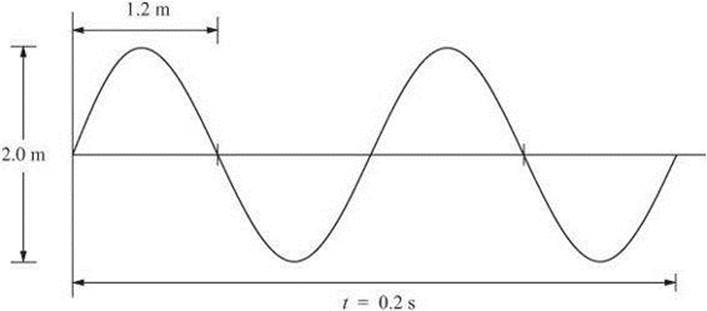
8. What is the amplitude of the wave shown?
(A) 0.2 m
(B) 1.0 m
(C) 1.2 m
(D) 2.4 m
(E) 4.0 m
9. What is the wavelength of the wave shown?
(A) 0.2 m
(B) 1.0 m
(C) 1.2 m
(D) 2.4 m
(E) 4.0 m
10. What is the frequency of the wave shown?
(A) 2 Hz
(B) 6 Hz
(C) 10 Hz
(D) 12 Hz
(E) 16 Hz
QUESTION ANSWERS AND EXPLANATIONS
1. A A mechanical wave is one that travels through a physical medium, such as water or air. An electromagnetic wave is one that does not require a medium and can therefore travel through a vacuum.
2. B The particles of the medium vibrate perpendicular to the direction in which a transverse wave travels. The particles, therefore, vibrate at an angle of 90° to the motion of the wave.
3. B Rearrange the equation for speed equation ![]() as
as ![]() .
.
4. A The key to solving this problem is recognizing that the frequency of the wave is not required in the calculation. Rearrange the speed equation![]() as
as ![]() .
.
5. D The waves interfere destructively where the waves are on opposite sides of the axis, which occurs at point D.
6. C Nodes occur where destructive interference occurs and the net displacement is zero. Therefore, the nodes occur along the horizontal line. The high and low points are antinodes.
7. D The Doppler effect results in a change in the apparent pitch of the sound because the sound waves pile up in front of the train, causing the frequency to increase.
8. B The amplitude is the maximum displacement of rest of the particles of the medium. It is the distance from the resting position, or horizontal line, to either a crest or a trough. The total distance from crest to trough is shown as 2.0 m, so the amplitude must be 1.0 m.
9. D The wavelength is the distance between two consecutive similar points. The distance represented as 1.2 m is half of the wavelength of this wave, so the total wavelength must be 2.4 m.
10. C The frequency measures the number of waves that pass a point per second. Two complete waves pass in 0.2 s, so the frequency is 2 cycles/![]() .
.