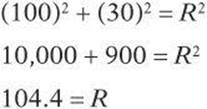VECTORS - PHYSICS TOPIC REVIEW - SAT Subject Test Physics

SAT Subject Test Physics (2012)

PART III. PHYSICS TOPIC REVIEW

Chapter 2. VECTORS

Understanding the nature of the measurements presented on SAT Physics will help you relate quantities and perform calculations correctly. In this chapter, you will review specific types of measurements known as vectors.

VECTORS AND SCALARS

Some of the measurements you will encounter are scalar quantities, which are quantities that have only magnitude associated with them. Other quantities are vector quantities, which have both magnitude and direction.

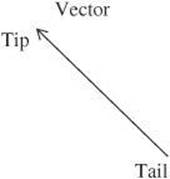
Vectors are represented by arrows in which the length of the arrow relates to the magnitude and the direction indicates the direction of the vector. You will generally see the point of the arrow described as the tip of the vector and the other ends as the tail, or base.

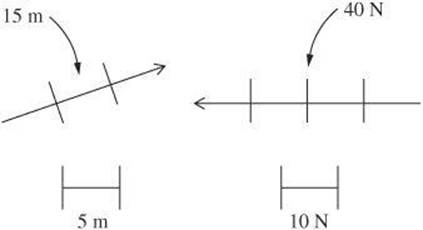
Some vector diagrams include a scale that relates the size of the drawing to actual measurements. The following examples represent displacement in meters and force in newtons. Both topics will be reviewed in later chapters.

Vectors can be represented in several different ways. One common method is as a letter with an arrow above it, such as . SAT Physics uses a boldface letter written in italic print, such as F. The magnitude of a vector is also written in italic print, but not in boldface.

Vector Addition

Two or more vectors can be combined to find the resultant R through addition. There are two basic methods of vector addition that each yield the same result: the parallelogram method and the tip-to-tail method.

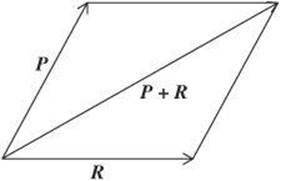
Parallelogram Method To use this method, draw the vectors so that they extend from the same point and use the same scale. Use the vectors as two sides of a parallelogram and complete the figure by adding the two missing sides. The diagonal of the parallelogram is the sum of the vectors as shown in the diagram.

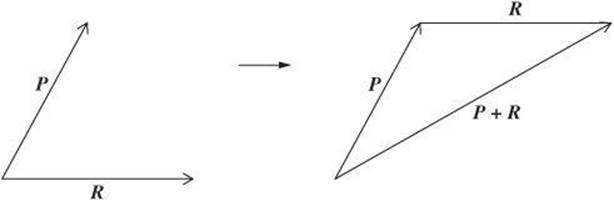
Tip-to-Tail Method To use this method, place the tail of one vector at the tip of the other. Then draw a vector from the tail of the first vector to the tip of the other. The vector you draw is the sum.

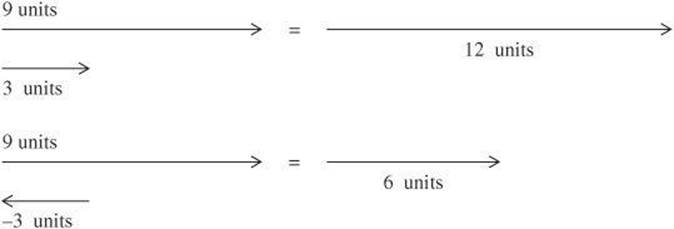
If the diagram includes a scale, you may be able to quickly determine or at least estimate the magnitude of the sum. In other cases, you will need to calculate the magnitude. Keep in mind that SAT Physics will not require you to complete complex calculations that require calculators or trigonometry. However, in many cases you will be able to determine the magnitude of the sum relatively simply. For example, if the vectors are parallel, you can use simple arithmetic.

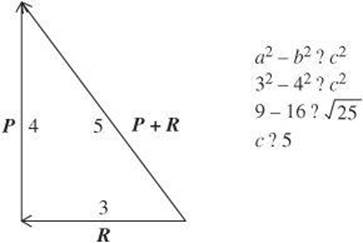
If vectors are perpendicular, you can use the Pythagorean Theorem to find the magnitude of the resultant.

Resolution of Vectors

A single vector may be resolved, or broken down, into its components. Vectors are commonly resolved into horizontal and vertical components so that trigonometric relationships can be used. The sum of the components is the original vector.

Consider a vector F at an angle to the horizontal. To find the components, draw a horizontal vector and a vertical vector.

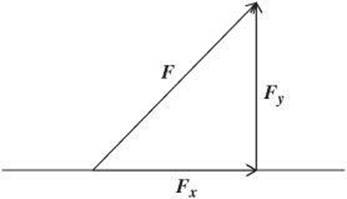
The component vectors form a right triangle. Therefore, you can solve for the magnitude of each component.

Example:

A force is exerted at an angle of 30° with the horizontal. If the magnitude of the force vector is 20 newtons, what are the vertical and horizontal components?

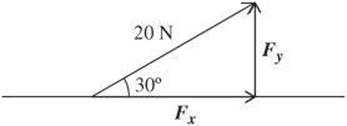
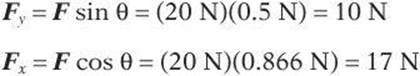
Vector Multiplication

You may encounter problems that involve vector multiplication. There are two basic forms of vector multiplication: dot product and cross product.

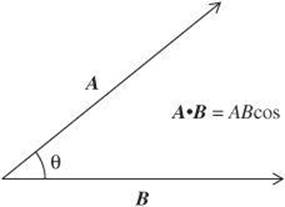
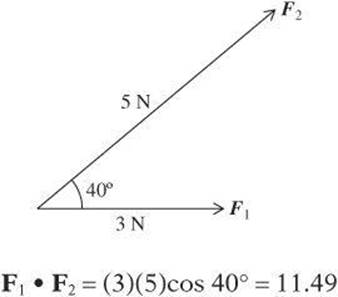
Dot Product The dot product, or scalar product, combines vectors in such a way that the result is a scalar. Essentially, the dot product involves multiplying the component of one vector in the direction of the other by the magnitude of the other vector. Notice in the diagram that the dot product of the vectors equals the product of the magnitude of the vectors multiplied by the cosine of the angle between them.

Example:

Find the dot product of the vectors F₁ and F₂.

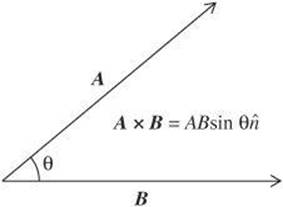
Cross Product The cross product, or vector product, combines vectors in such a way that the result is a vector. The resulting vector is perpendicular to both of the original vectors. Thus, finding the cross product involves three dimensions. Note in the following example that the cross product is equal to the product of the magnitudes of the vectors times the sin of the angle between them and , which is a unit vector perpendicular to both vectors.

To determine the direction of , you need to use the right-hand rule. According to this rule, point your forefinger in the direction of A and your middle finger in the direction of B. Your thumb will point in the direction of vector .

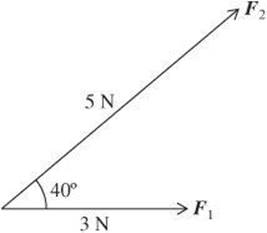
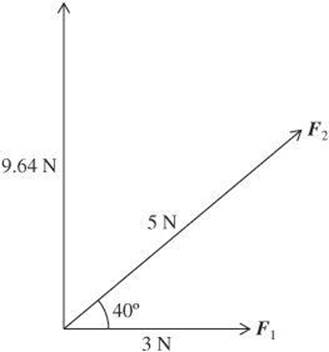
Example:

Find the cross product of the vectors F₁ and F₂.

Test-Taking Hint

If you are right-handed, you may be tempted to use your left hand as you are writing on the SAT Physics exam. However, when directions are chosen according to the right-hand rule, you must use your right hand to determine relationships. Using your left hand will result in incorrect answers.

REVIEW QUESTIONS

Select the choice that best answers the question or completes the statement.

1. Which of the following examples describes a vector quantity?

(A) It took 9.2 minutes for the water to boil.

(B) She exerted a force of 5 newtons downward on the board.

(D) An acorn moved about 10 meters.

(E) The temperature rose 23°C.

2. Vector A has a magnitude of 4 in the upward direction and B has a magnitude of 3 in the downward direction. What is the value of 2A + B?

(A) 2 in the upward direction

(B) 6 in the upward direction

(D) 5 in the downward direction

(E) 11 in the downward direction

3. Which vector represents A + B?

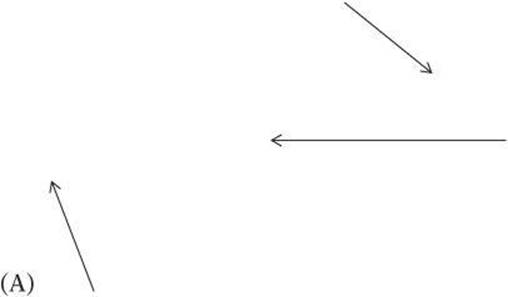
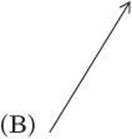
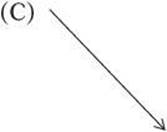
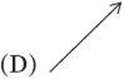
Questions 4 and 5 relate to the diagram below, which shows a person exerting a force of 50.0 N on a sled at an angle of 40.0°.

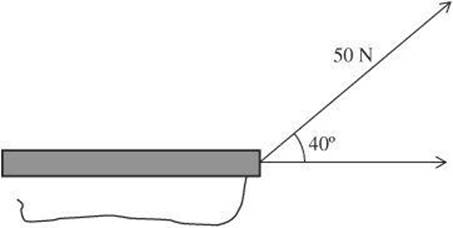
4. What is the horizontal component of the force?

(A) 25.0 N

(B) 32.5 N

(D) 46.8 N

(E) 50.6 N

5. What is the vertical component of the force?

(A) 11.7 N

(B) 16.0 N

(D) 32.1 N

(E) 45.6 N

6. Vector A has a magnitude of 12.0 and Vector B has a magnitude of 3.0. If the vectors are at an angle of 60.0°, what is the dot Product ?

(A) 2

(B) 4

(D) 18

(E) 36

7. Vector A has a magnitude of 9.0 and Vector B has a magnitude of 3.0. If the vectors are at an angle of 30.0°, what is the magnitude of the cross product A × B?

(A) 13.5

(B) 16.2

(D) 27.0

(E) 32.0

8. Vector A points into the page. Vector B points downward, parallel to the plane of the page. Which direction describes the cross product A × B?

(A) out of the page

(B) to the left, parallel to the plane of the page

(D) upward, parallel to the plane of the page

(E) into the page

9. Which statement about A × B is true?

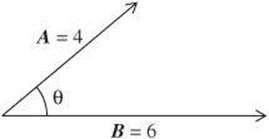
(A) It is in the plane of the page.

(B) Its magnitude must be greater than 24.

(D) It is a vector that points into the page.

(E) It is equal in magnitude to the sum of the magnitudes of A and B.

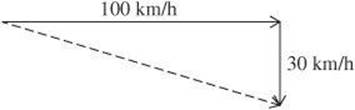
10. An airplane flies with a velocity of 100 km/h directly east. A wind blows on the airplane with a velocity of 30 km/h directly north. What is the magnitude of the resultant velocity of the airplane?

(A) 0 km/h

(B) 30 km/h

(D) 90 km/h

(E) 100 km/h

QUESTION ANSWERS AND EXPLANATIONS

1. B A vector quantity has both magnitude and direction. All of the answer choices except for B include magnitude only. The force is described by its magnitude, or 5 N, and direction, or downward.

2. C The magnitude of the vector in the upward direction is doubled, 8. Adding the magnitude of the vector in the downward direction is the same as subtraction. So .

3. E Placing the vectors tip-to-tail shows the resulting vector.

4. C The horizontal component is found by .

5. D The vertical component is found by .

6. D The dot product .

7. A The cross product .

8. B According to the right-hand rule, if the forefinger points in the direction of A and the middle finger points in the direction of B, the thumb points in the direction of the cross product.

9. D The cross product is a vector that is perpendicular to both of the original vectors so it cannot be in the same plane. It equals the product of 24 and sin θ, where θ, is less than 90°. Therefore, the magnitude would be less than 24. The angle it makes with A is the same as the angle it makes with B. It is not found by adding the magnitudes of the vectors.

10. E Draw the vectors representing the velocity of the airplane and the wind tip-to-tail. Use the Pythagorean Theorem to find the resultant.