SAT For Dummies

Part IV

Take a Number, Any Number: The Mathematics Sections

Chapter 19

In This Chapter

Practicing some guided questions about probability, statistics, and logic

You can count on at least a couple of probability, statistics, and logic problems showing up on your particular version of the SAT. Don’t freak out! Now’s the time to practice with the help of the two sets in this chapter. After you complete each question in the first set, check your answers and read the explanations of any problem you answered incorrectly. (The answers immediately follow each question.) Don’t cheat, though! Use a piece of paper to cover the answers as you work through the problems. Then, if you need more practice, hit Set 2, which is set up more like the real test, with the answers coming in a section separate from the questions themselves. Turn to Chapter 18 for a refresher course in any topic that stumps you in either set.

Set 1: Trying Your Hand at Some Guided Questions

Note: Questions 1 and 7 are grid-ins, which means you don’t get any answers to choose from. See Chapter 11 for tips on answering grid-ins.

1. A school cafeteria offers two soups, three main dishes, and four desserts. Find the total number of possible meals consisting of one soup, one main dish, and one dessert.

The correct answer is 24. Using the counting principle, 2 × 3 × 4 = 24.

2. The chance of rain tomorrow is 1⁄4. As a percentage, what is the probability that it will not rain tomorrow?

(A) 4%

(B) 25%

(C) 40%

(D) 75%

(E) 96%

As a percentage, 1⁄4 = 25%. The probability of an event not happening equals 100% minus the probability of it happening, and 100% – 25% = 75%. Choice (D) is correct.

3. In a special deck of 20 cards, 8 cards are red on both sides, 7 cards are blue on both sides, and the other 5 cards are red on one side and blue on the other side. If a student picks a card and places it on his desk, what is the probability that the side facing up is blue?

(A) 19⁄40

(B) 12⁄20

(C) 7⁄40

(D) 7⁄20

(E) 12⁄40

This one’s a little tricky. Even though there are 20 cards, the question asks only about the side of the card facing up, and there are 20 × 2 = 40 possible sides. The 7 cards that are blue on both sides represent 7 × 2 = 14 blue sides, and there are 5 cards with one blue side. 14 + 5 = 19, so the probability is 19⁄40. Choice (A) is correct.

Problems 4, 5, and 6 use the following graphs:

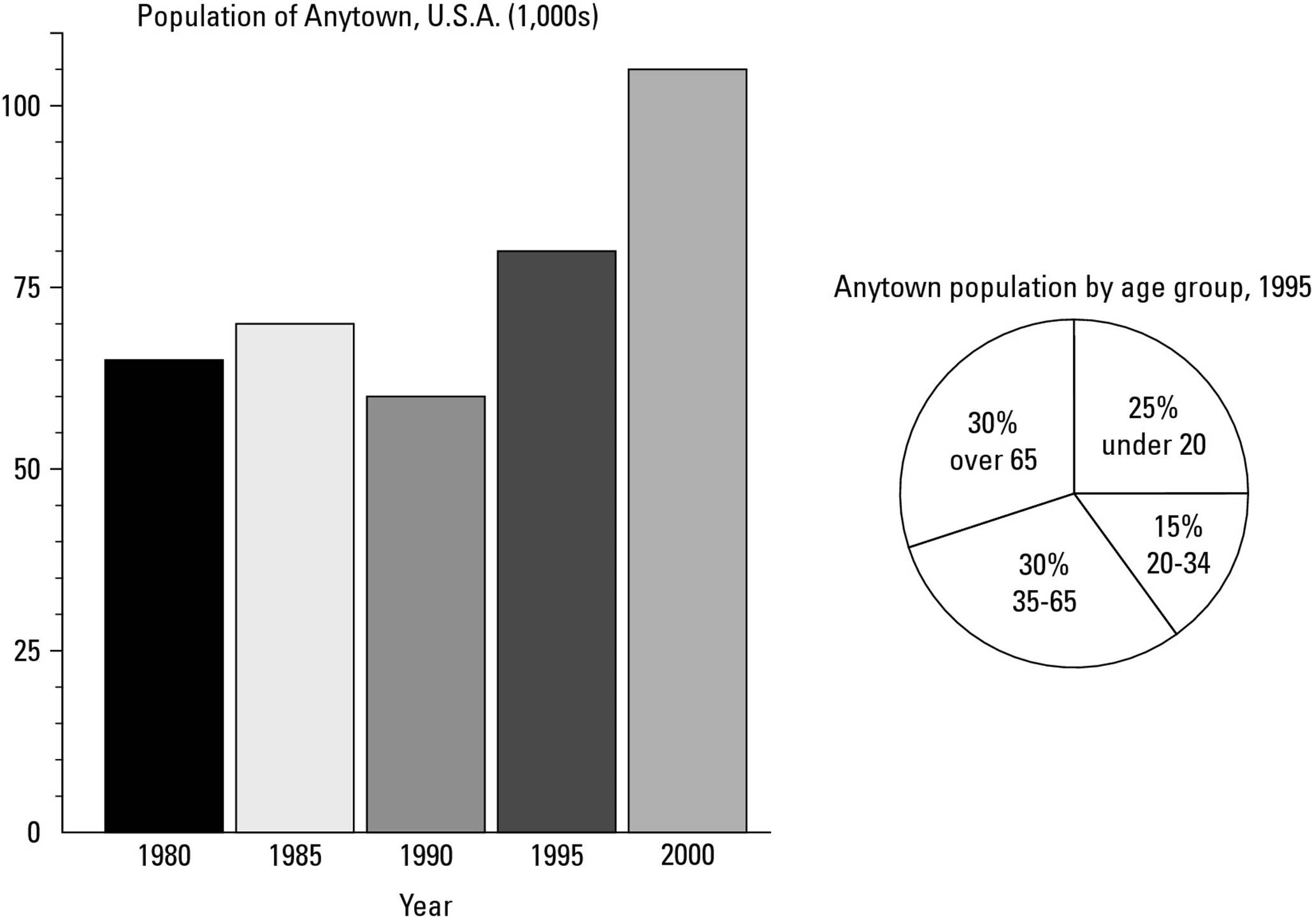
4. In 1990, what was the approximate number of Anytown residents over the age of 65?

(A) 55,000

(B) 50,000

(C) 25,000

(D) 14,000

(E) It cannot be determined from the graphs.

Don’t trip over this one. You can tell from the bar graph that in 1990 Anytown had approximately 60,000 total residents, but the pie graph tells you only about the ages of the residents in 1995. You have no way to determine anything about the ages of Anytown residents in 1990, so Choice (E) is correct.

5. During which five-year period did Anytown have the greatest percent increase in population?

(A) 1980–1985

(B) 1985–1990

(C) 1990–1995

(D) 1995–2000

(E) It cannot be determined from the graphs.

You can throw out (B) right away because the population decreased. Don’t get fooled by (D); although the population went up by 25,000 people, the percent change was 25,000 ÷ 80,000 = 0.3125, or 31%. But from 1990 to 1995, the population increased by 20,000 from an original population of 60,000. That’s 20,000 ÷ 60,000 = 0.3333, or 33%. Thus, (C) is correct.

6. In 1995, roughly how many Anytown residents were between the ages of 20 and 65?

(A) 45

(B) 15,000

(C) 30,000

(D) 36,000

(E) 45,000

A look at the pie chart tells you that 30 + 15, or 45% of the residents were between 20 and 65 in 1995. Because there were 80,000 residents, change 45% into 0.45, and 0.45 × 80,000 = 36,000. Give it up for (D).

7. A bag contains red, blue, and green marbles. The probability of picking a red marble is 1⁄2; the probability of picking a blue marble is 1⁄3. If the bag holds seven marbles that are green, find the total number of marbles in the bag.

Your answer here is 42. To do this one, you need a little algebra. Because the probability of picking a red marble is 1⁄2, half of the marbles are red. Similarly, 1⁄3 of the marbles must be blue. So 1⁄2 of the marbles, plus 1⁄3 of the marbles, plus the seven green marbles, is the number you’re looking for. If you let x represent the total number of marbles, you can write

.

Because fractions are annoying, multiply everything by 6 to get 3x + 2x + 42 = 6x. This equation gives you 5x + 42 = 6x, so x = 42. Another way to think about this question: The red and blue marbles represent 1⁄2 + 1⁄3 = 5⁄6 of the marbles. That leaves 1 – 5⁄6 = 1⁄6 of the marbles to be green, and 7 is 1⁄6 of 42.

8. If a student picks a square at random on the following grid, what is the probability that he picks a square that is not shaded?

(A) 3⁄5

(B) 3⁄8

(C) 2⁄5

(D) 5⁄8

(E) 3⁄10

Twenty-five of the 40 squares are shaded, leaving 40 – 25 = 15 unshaded. 15⁄40 reduces to 3⁄8. Choice (B) is correct.

9. Which graph could represent the line of best fit for this scatterplot?

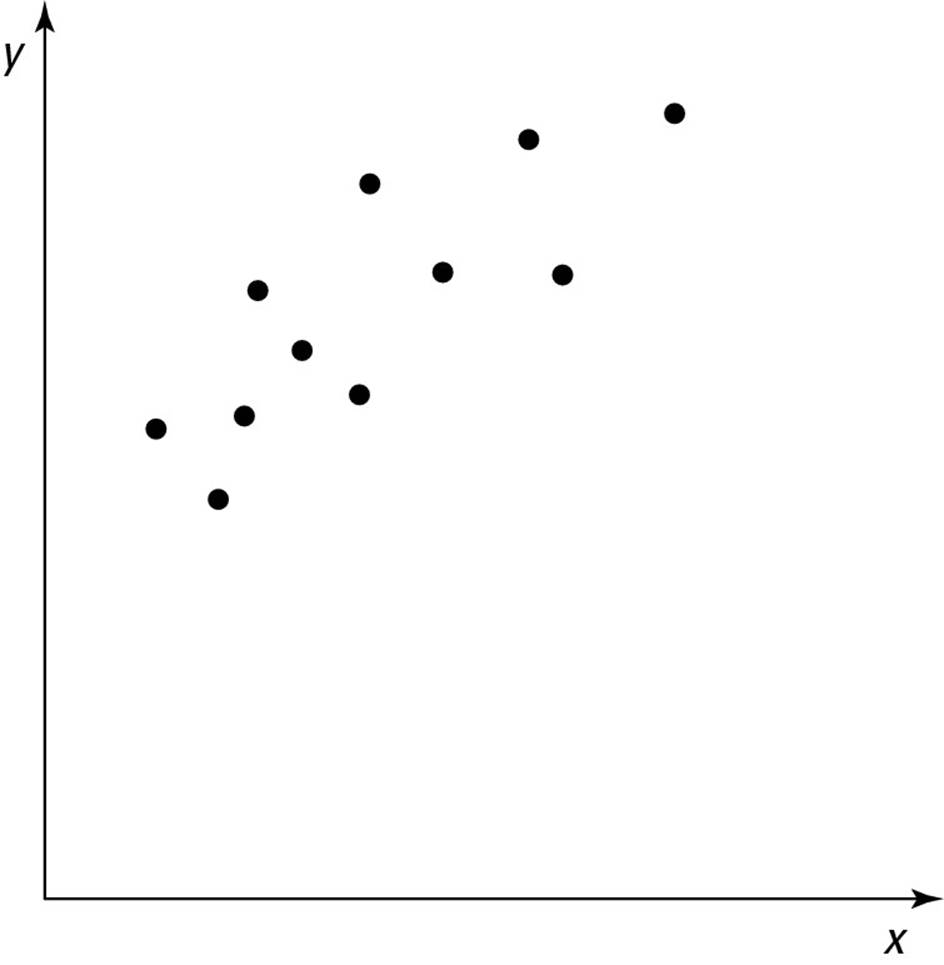
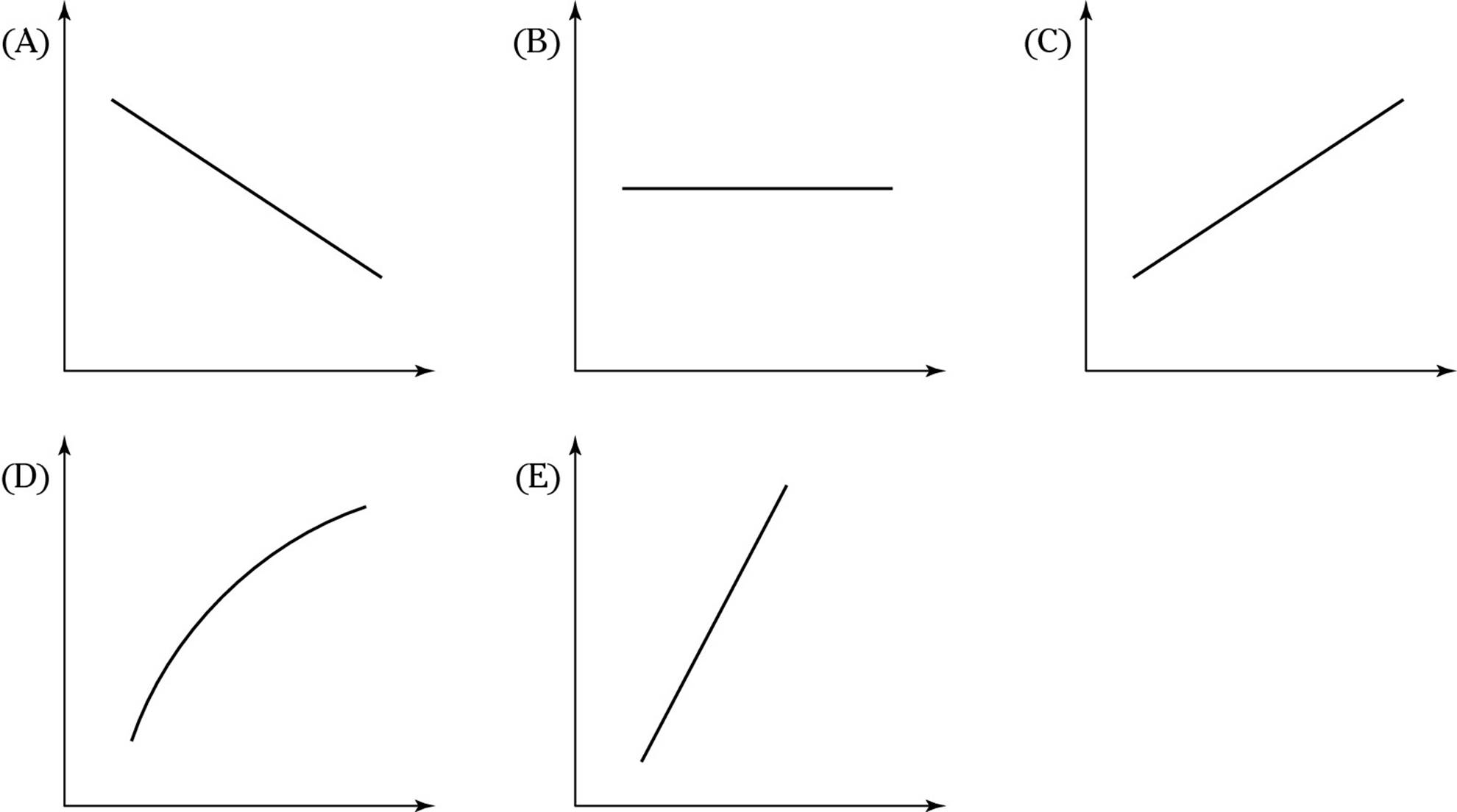
As long as you remember what the “line of best fit” means, this one is easy (see Chapter 18 if you don’t). Choice (C) is correct.

10. Adrianna, Bob, Chris, and Darrell all arrive at school between 7:30 and 8:00.

Chris was late to school, but Bob was not.

Darrell arrived ten minutes after Adrianna.

Bob didn’t see Adrianna when he came into school.

Based on this information, which student(s) could have arrived at exactly 7:30?

(A) only Adrianna

(B) only Bob

(C) either Adrianna or Bob

(D) only Chris

(E) none of them

You don’t know what time the school day starts, but the first clue tells you that Chris must have arrived later than Bob, so Chris couldn’t have arrived at 7:30, but (from this clue) Bob could have. The same logic applies to the second clue: Darrell arrived after Adrianna, so Darrell couldn’t have been there at 7:30, but Adrianna could have. The third clue is just the SAT makers (okay, me) messing with you; Adrianna might have already been in the building, or she might not have been, but we just can’t tell. So Choice (C) is correct because either of them might have arrived at 7:30; in fact, they might have both arrived then, if the school has more than one door.

Set 2: Practicing Some Questions on Your Own

1. A certain data set has a mean of 20, a median of 21, and a mode of 22. Which measurement must occur in the data set?

I. 20

II. 21

III. 22

(A) I only

(B) II only

(C) III only

(D) II and III

(E) none of the above

2. A student has a median score of 83 on five tests. If she scores 97 and 62 on her next two tests, her median score will

(A) increase to 90

(B) decrease to 82

(C) decrease to 79.5

(D) remain the same

(E) It cannot be determined from the ­information given.

3. Alicia picks a number from the set {1, 2, 3, 4, 5, 6}. Michelle picks a number from the set {3, 4, 5, 6, 7, 8}. What is the probability that they select the same number?

(A) 1⁄6

(B) 4⁄36

(C) 4⁄6

(D) 16⁄36

(E) 4⁄8

4. A magazine did a study of ten cars, comparing the number of miles each car could go on a full tank of gas. Their results are shown below. Of the labeled points, which one represents the car that goes the farthest per gallon of gas?

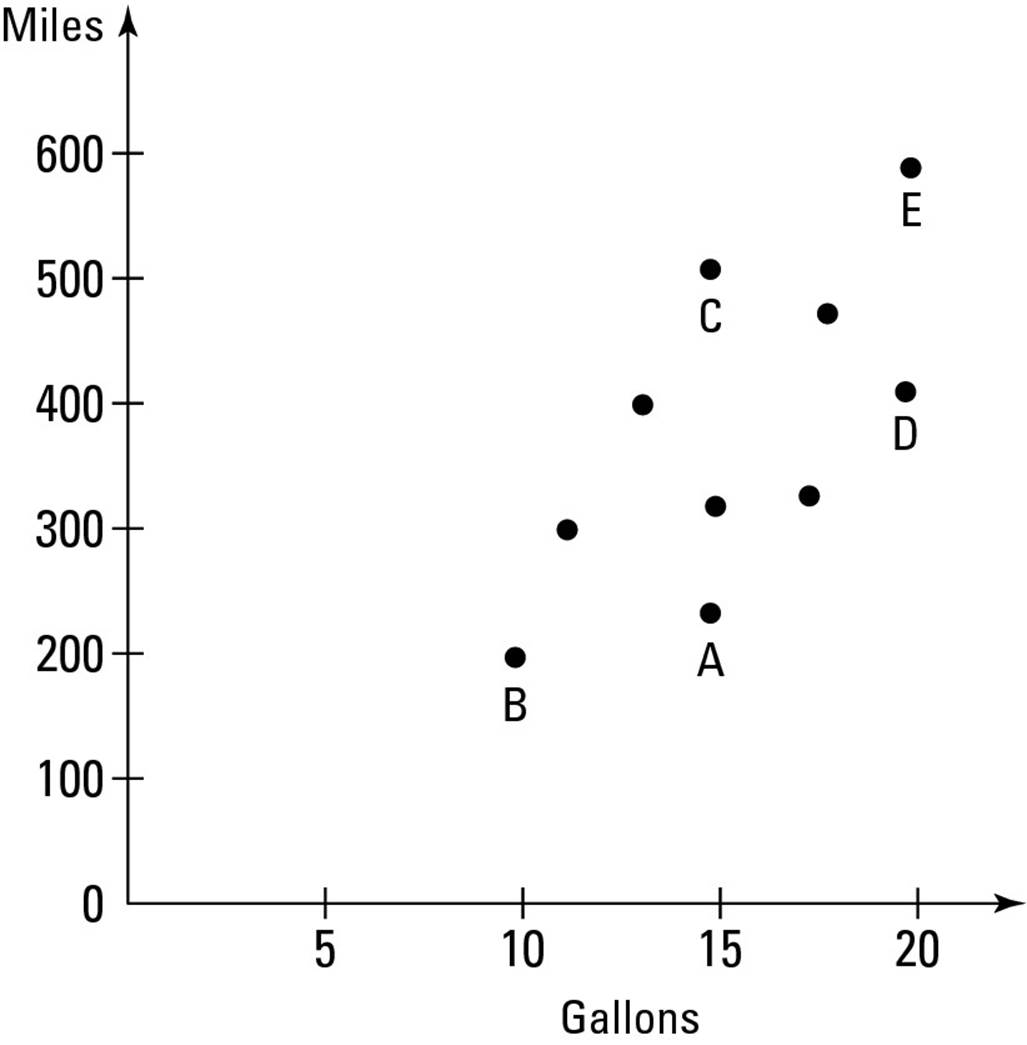
(A) A

(B) B

(C) C

(D) D

(E) E

5. If a two-digit number is picked at random, what is the probability that the number chosen is a perfect square?

(A) 6⁄90

(B) 10⁄100

(C) 7⁄91

(D) 6⁄89

(E) 9⁄99

6. A class contains five boys and seven girls. In how many ways can a teacher line up two boys and two girls, in that order?

(A) 35

(B) 140

(C) 210

(D) 840

(E) 1,225

7. A junior is choosing her classes for senior year. If she takes calculus, she can also take either history or English, but not both. If she takes psychology in the first semester, she cannot take sociology or creative writing. If she takes psychology in the second semester, she cannot take calculus, but can take any elective she wants during the first semester. Based only on this information, which of the following is not a possible choice of courses for her?

(A) English, calculus, psychology, statistics

(B) History, sociology, psychology, English

(C) Creative writing, psychology, history, English

(D) Calculus, psychology, creative writing, history

(E) Psychology, sociology, English, statistics, creative writing

8. The following dartboard consists of three circles with the same center. If the circles have radii of 6, 8, and 10 inches, what is the probability that a dart that hits the board lands in the shaded ring?

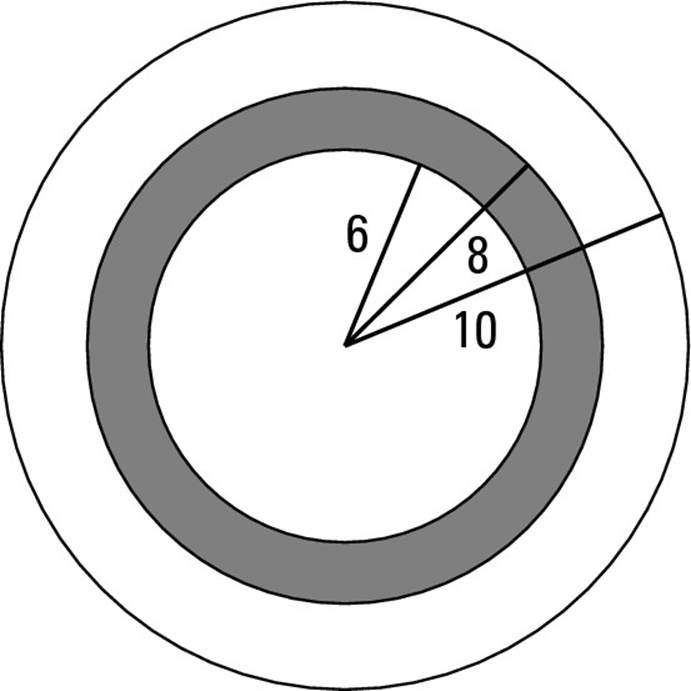
(A) 7⁄25

(B) 4⁄5

(C) 3⁄4

(D) 9⁄16

(E) 16⁄25

9. A student has taken three tests, with an average (arithmetic mean) of 82. What grade must she receive on her next test in order to have an overall average of 85?

(A) 85

(B) 88

(C) 90

(D) 94

(E) 97

Answers to Set 2

1. C. If you remember how to compute the three ms, you’ll realize that the mean and median don’t have to be in the data set. (Look in Chapter 18 for more on mean, median, and mode.) But because the mode is the most common measurement, it must be in the set. Thus, Choice (C) is correct.

2. D. The median is the score in the middle. If 83 is in the middle, adding a 97 on one side and a 62 on the other side doesn’t change where the middle is. The correct answer is (D).

3. B. First determine the total number of possibilities. Using the counting principle, you know you have 6 × 6 = 36 possibilities. Because the two sets overlap at 3, 4, 5, and 6, the girls may pick the same number in only four ways. Hence, the answer is 4⁄36. (Notice that the fraction isn’t always reduced in probability questions.) Choice (B) is correct. Another way to look at it: The first girl has a 4⁄6 chance of picking a number that the second girl could match. If the first girl picks a number that can be matched, the second girl has a 1⁄6 chance of picking the same number. The math: 4⁄6 × 1⁄6 = 4⁄36.

4. C. Car C travels approximately 500 miles on 15 gallons, for 500⁄15 or around 33 miles per gallon. Although Car E goes almost 600 miles, it needs 20 gallons, so it gets less than 30 miles per gallon. The other cars all travel fewer than 30 miles per gallon. Choice (C) is correct.

5. A. As usual in a probability question, you need to start by determining the total number of two-digit numbers. The two-digit numbers run from 10 to 99. The formula you can use here is as follows: The total is one more than the difference of the two numbers, or 99 – 10 + 1 = 90. The two-digit numbers that are perfect squares are 16, 25, 36, 49, 64, and 81. Pat yourself on the back if you answered (A).

6. D. Because cloning people isn’t a reality just yet, the teacher can’t pick the same person twice. So the teacher has five choices for the first boy, but only four left for the second. Similarly, he has seven choices for the first girl and six for the second. Using the counting principle, you know the answer is 5 × 4 × 7 × 6 = 840. Choice (D) is correct.

7. D. Start by making a list of combinations that are impossible:

Calculus, English, history

First-semester psychology, sociology

First-semester psychology, creative writing

Second-semester psychology, calculus

Now consider the choices: Choice (A) is fine, if she takes psychology in the first semester. Choice (B) is okay if she takes psychology in the second semester. Choice (C) is fine, if she takes psychology in the second semester. Choice (D) is a problem. If she takes psychology in the first semester, then creative writing is out. But if she takes it in the second semester, then calculus is out. Choice (E) is fine if she takes psychology in the second semester. Choice (D) is the correct answer.

8. A. The shaded ring has an outer radius of 8 and an inner radius of 6. So the area of the shaded ring is the area of the radius-8 circle minus the area of the radius-6 circle, or π(8)² – π(6)² = 64π – 36π = 28π. The entire dartboard has a radius of 10, so its area is π(10)² = 100π, and the probability equals 28π⁄100π = 28⁄100 = 7⁄25. Choice (A) is correct.

9. D. The formula average score × number of scores = total score helps you answer this problem. The student wants to end up with an average score of 85 on four tests, for a total score of 85 × 4 = 340. The student’s total number of points on the first three tests is 82 × 3 = 246. So to make up the difference, she needs 340 – 246 = 94 points on her next test to get (1) the car keys and (2) permission to stay out past 7 p.m. Choice (D) is correct.