Cracking the SAT
Part III
How to Crack the Math Section
Chapter 16
Putting It All Together
Now that you have reviewed the mathematical concepts you need to know for the SAT, it is time to start practicing what you’ve learned. This chapter contains a comprehensive practice drill on which you can practice your skills and techniques. Good luck!
PUTTING IT ALL TOGETHER…
Here’s your chance to combine everything you learned in the math chapters and give yourself some extra drills before the practice tests. Remember to practice the techniques we’ve taught you, even if you could arrive at the answer in a different way. This is the only way to improve your problem recognition skills (knowing what technique to use on what type of problem).
The problem numbers represent where you would see them on the actual SAT. All numbers of multiple-choice questions are based on a 25-minute section, so you can use that as a gauge for recognizing question difficulty. The answers and explanations are located in Part VI (this page).
Good luck!
13. If a < b and a2 – 2ab + b2 = 169, what is the value of a – b?
15. If a is 63% of x and c is 
of x, which of the following is the closest equivalent of the ratio of a to c?
(A) 0.006
(B) 0.236
(C) 0.381
(D) 0.595
(E) 1.680
11. In right triangle ABC, the longest side, AB, is 4 feet long, and angles BAC and ABC are equal. What is the perimeter of the triangle in feet?
(A) 8
(B) 4
(C) 4 + 4
(D) 12
(E) 8 + 4
18. There are 5 cyclists in a race. If the first-place finisher receives a gold medal, the second-place finisher receives a silver medal, and the third-place finisher receives a bronze medal, how many different permutations are possible for the medal winners?
(A) 5
(B) 12
(C) 20
(D) 50
(E) 60
12. If a + 2b = 10, and b – a = 2, what is the value of b?
(A) 10
(B) 8
(C) 6
(D) 4
(E) 2
8. If the perimeter of a square is 28, what is the length of the diagonal of the square?
(A) 2
(B) 7
(C) 7
(D) 14
(E) 28
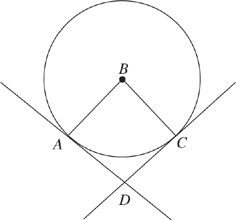
Note: Figure not drawn to scale.
17. In the figure above, DA and DC are tangent to the circle with center B at points A and C, respectively. If ABC = 
ADC, what is the degree measure of ∠ADC ?
(A) 40
(B) 51
(C) 129
(D) 140
(E) 154
10. A photographer is arranging 5 photographs in a row from left to right for a display. If all 5 photographs will be used, how many different arrangements can the photographer make?
(A) 5
(B) 24
(C) 25
(D) 120
(E) 390,625
19. At Ernie’s Fruit Stand, 3 apples and 5 cherries cost $1.25. 15 apples and 100 cherries cost $9.25. What is the cost of 6 apples and 35 cherries?
(A) $3.25
(B) $3.50
(C) $3.62
(D) $4.00
(E) $5.25
7. According to local safety regulations, no transit bus may carry more than 66 people in it at one time. Right now, there are 42 people on a particular transit bus. At the next stop, n people enter the bus, but no one exits. If the total number of people on that transit bus is not over the limit, in terms of n, how many people are on the bus?
(A) n + 42 ≤ 66
(B) n + 42 ≥ 66
(C) n – 42 ≤ 66
(D) n – 42 ≥ 66
(E) n ≥ 66 – 42
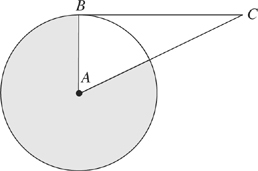
Note: Figure not drawn to scale.
18. The circle above with center A has an area of 21. BC is tangent to the circle with center A at point B. If AC = 2AB, what is the area of the shaded region?
14. If f(x) = |x| + 1 and g(x) = x – 3, what is the value of f(g(1))?
(A) –2
(B) –1
(C) 1
(D) 2
(E) 3
15. If f(x) = 
for all values of x ≥ 0, and f(x) = x2 + 2 for all values of x < 0, what is the sum of f(–3) and f(8)?
(A) 5
(B) 11
(C) 14
(D) 68
(E) 77
6. At a certain bookstore, hardcover books cost 3x dollars each, and paperback books cost 2x dollars each. If Katey purchased 6 books and spent a total of 14x dollars, how many hardcover books did she buy?
(A) One
(B) Two
(C) Three
(D) Four
(E) Five
16. One sheet of metal can be melted down to make a spherical ball with a radius of 2 centimeters. How many such sheets would have to be melted down to make a spherical ball of radius 6 centimeters? (The volume V of a sphere with radius r is given by V = 
πr3.)
(A) 3
(B) 9
(C) 16
(D) 27
(E) 216
17. Let f(a, b) = a2 – b2. If f(5, d) = 9, and d is positive, what is the value of d?
Note: Figure not drawn to scale.
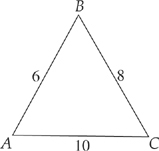
13. What is the measure, in degrees, of the largest angle in the above triangle?
20. If the product of x2 – 6x + 5 and 2x2 – 7x + 3 is 0, then x could equal any of the following numbers EXCEPT
(A) 
(B) 1
(C) 2
(D) 3
(E) 5
12. Jon is making omelets. He has 3 different spices, 4 different vegetables, and 2 different types of eggs. If he will use one spice, one vegetable, and one type of egg, how many combinations of these ingredients can he make?
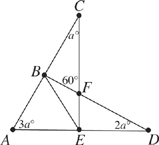
17. In the figure above, AC, CE, and BD intersect at the points shown above. What is the value of a?
18. If n is an integer that satisfies the inequality above, what is the sum of the largest possible value of n and the smallest possible value of n?
(A) 2
(B) 4
(C) 100
(D) 106
(E) 117
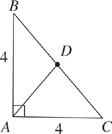
12. In the figure above, AB = AC = 4 and ∠BAC and ∠ADC are right angles. What is AD?
(A) 2
(B) 2
(C) 4
(D) 4
(E) 8
n, 2n, 3n, 4n
7. If n is a negative integer, which of the numbers above is the greatest?
(A) n
(B) 2n
(C) 3n
(D) 4n
(E) It cannot be determined from the information given.
20. Carlos and Katherine are estimating acceleration by rolling a ball from rest down a ramp. At 1 second, the ball is moving at 5 meters per second (m/s); at 2 seconds, the ball is moving at 10 m/s; at 3 seconds, the ball is moving at 15 m/s; and at 4 seconds, it is moving at 20 m/s. When graphed on an xy-plane, which equation best describes the ball’s estimated acceleration where y expresses speed and x expresses time?
(A) y = 5x + 5
(B) y = 25x
(C) y = –5x + 5
(D) y = 5x
(E) y = (4x + 1)2 + 5
17. The average (arithmetic mean) number of computers fixed by a technician was 15 per day for the first 20 days of the month. After another 10 days, the average number of computers fixed over all 30 days was 18 per day. What was the average number of computers fixed in the last 10 days?
(A) 24
(B) 27
(C) 29
(D) 32
(E) 35
20. If y = 3x and x and y are both integers, which of the following is equivalent to 9x + 3x + 1?
(A) y3
(B) 3y + 3
(C) y(y + 3)
(D) y2 + 3
(E) 3(y + 3)