SAT Test Prep

CHAPTER 6
WHAT THE SAT MATH IS REALLY TESTING

1. Mapping Problems

2. Analyzing Problems

3. Finding Patterns

4. Simplifying Problems

5. Connecting to Knowledge

6. Finding Alternatives

7. Thinking Logically

8. Checking Your Work

Lesson 1: Mapping Problems

What Is Mapping?

Mapping a problem means orienting yourself to the problem and representing its information. It”s like pulling out a map before you start a trip. The map shows you where you”re going but not how to get there. On some tough SAT math problems, half the battle is “mapping”—orientingyourself to the problem and figuring out what it”s asking.

Tips for mapping tough SAT math problems:

• Write out any diagrams, equations, or tables that represent the key information in the problem. You don”t get neatness points on the SAT—good test-takers scribble all over the test booklet. Writing things down helps you to keep track of the information as well as your thought process.

• Notice any restrictions on the unknowns. For instance, do they have to be integers or positive numbers or multiples of some number? Are they measures of angles or segments or areas in a figure? Underline key restrictions.

• Know the definitions of special terms such as primes, integers, factors, multiples, perimeter, and so on, and underline these terms when you see them.

• Notice whether any unknowns can take any values that you choose or have only one particular value that you have to find. You can solve many complicated-looking problems by just choosing values for the unknowns!

• Read carefully and notice exactly what the problem is asking for. Does it ask you to solve an equation? Find the value of an expression? Find an area? Underline what the problem is asking you to find so that you don”t lose track of it.

• Notice whether the question is multiplechoice, and if so, notice the range of the answer choices. If the answers are far apart, you might be able to just estimate an answer to zero in on the right choice. Also, notice how the choices are expressed. Are they fractions, decimals, radicals,algebraic expressions? Noticing this often helps you to see what you have to do to get the answer.

Watch for the Common Mix-Ups

Even the best students sometimes miss questions because they misinterpret key terms in the problem. You can avoid this by underlining these key terms and thinking about the terms they are commonly confused with.

• A perimeter is the distance around a figure. Don”t confuse it with area, which is the number of square units that fit inside a figure.

• The circumference formula for a circle is . Don”t confuse it with the area formula of a circle, which is . To avoid confusing them, remember that area is always measured in square units, so its formula contains the “square.”

• An odd number is any integer not divisible by 2. Don”t confuse it with a negative number, which is any number less than 0. These two are commonly confused because both of these words have a “bad” tone.

• An even number is any integer divisible by 2. Don”t confuse it with an integer in general, which is any positive or negative whole number. These two are commonly confused because when we talk of a number dividing another “evenly,” we really mean that it goes in an integer number of times, not necessarily an even number of times.

• A product is the result of a multiplication. Don”t confuse it with a sum, which is the result of addition.

Don”t Rush—Avoid Quick Gimmicks

Always read the whole problem carefully before deciding how to solve it. SAT math questions—especially medium and hard-level ones—are designed to trap students who don”t read carefully or who pigeon-hole questions too quickly. Getting an answer quickly doesn”t help if it”s the wrong answer.

Concept Review I: Mapping Problems

1. Describe what it means to “map” a problem.

2. Why is it important to consider the choices (in a multiple-choice question) as part of the problem?

Define the following terms, and indicate what terms they are sometimes confused with.

Equations or inequalities are powerful “mapping” tools. Translate the following statements into equations or inequalities. Be sure to specify the meanings of any unknowns you may use.

7. The sum of two consecutive odd numbers is 28.

8. Ellen is twice as old as Maria.

9. Last year, Jennifer was twice as old as Brian is now.

SAT Practice 1: Mapping Problems

Map each of the following problems before solving it. Use the space for scratchwork, and underline any key words in the problem. Then solve each problem.

1. The product of five consecutive even integers is 0. What is the greatest possible value of any one of these integers?

2. The perimeter of a rectangle is 28 inches, and its area is x square inches. If x is an even integer, what is the greatest possible value of x?

3. Carlos begins with twice as much money as David. After Carlos gives $12 to David, Carlos still has $10 more than David. How much money did they have combined at the start?

(A) $32

(B) $66

(C) $68

(D) $92

(E) $102

4. Corinne travels from home to work at an average speed of 50 miles per hour, and returns home by the same route at 60 miles per hour. It takes her 10 more minutes to get to work than it takes her to get home. How many miles is it from Corinne”s home to work?

(A) 25

(B) 35

(C) 50

(D) 75

(E) 90

Answer Key I: Mapping Problems

Concept Review I

1. To map means to represent the general problem situation and goal, either mentally or on paper.

2. Because the choices tell you the range of values to consider, as well as the form of the numbers (integers, fractions, etc.) and format (factored, decimal, etc.).

3. Odd means an integer not divisible by 2 and is sometimes confused with negative because of the “negative” tone of both words.

4. Even means an integer divisible by 2 and is sometimes confused with positive because of the “positive” tone of both words.

5. Perimeter means distance around a figure and is sometimes confused with area, which is the number of square units that fit inside a figure.

6. Integers are whole numbers and negative whole numbers and are sometimes confused with counting numbers, which are the positive integers: 1, 2, 3, 4,…

7. Let n be the smaller of the two numbers. Then the next odd number is , so an equation that says that the sum of two consecutive odd numbers is 28 is .

8. Let e stand for Ellen”s current age and m stand for Maria”s current age. An equation that says that Ellen is twice as old as Maria is .

9. Let j stand for Jennifer”s age now and b stand for Brian”s age now. Last year, Jennifer was j = 1 years old, so an equation that says that last year Jennifer was twice as old as Brian is now is .

SAT Practice 1

1. 8 If the product of a set of integers is 0, then one of the numbers must be 0. To maximize the value of any one of them, let 0 be the smallest of the integers. If they are consecutive even integers, they must be 0, 2, 4, 6, and 8. If your answer was 4, then you overlooked the fact that the numbers are even.

2. 48 Your first tool in mapping a geometry problem is a good diagram. This one has no diagram, so you must draw your own. Draw a rectangle, labeling its width w and its length l:

Since the perimeter of the rectangle is 28 inches, you can set up an equation: . Divide both sides of the equation by 2 to get . Since the area is x, you can set up the equation If x is even, then l and w can”t both be odd. (Can you see how we know that?) You should be able to see that the possible values for w and l are 2 and 12, 4 and 10, and 6 and 8. (Check them and see.) This means that x can have values of , , or . The greatest of these, of course, is 48.

3. E Let c be the number of dollars Carlos had to start and d be the number of dollars David had to start. The question asks for the value of . If Carlos begins with twice as much money as David, then . After Carlos gives $12 to David, he has dollars, and David has dollars. If Carlos still has $10 more than David, then .

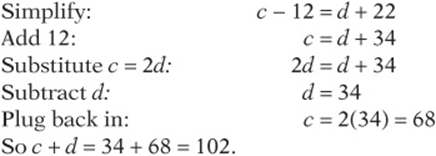
4. C To “map” this problem, you must know that distance = speed × time. You must find the number of miles from Corinne”s home to work, so call that d. If she travels from home to work at an average speed of 50 miles per hour, then it must take her d/50 hours, or . If she returns home at 60 miles per hour, it must take her . If it takes her 10 more minutes to get to work than it takes her to get home, then: