SAT Test Prep
CHAPTER 10
ESSENTIAL GEOMETRY SKILLS
Lesson 3: The Pythagorean Theorem
The Pythagorean Theorem
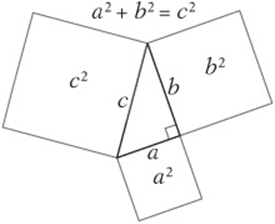
The Pythagorean theorem says that in any right triangle, the sum of the squares of the two shorter sides is equal to the square of the longest side. If you know two sides of any right triangle, the Pythagorean theorem can always be used to find the third side.
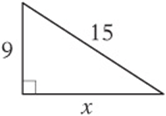
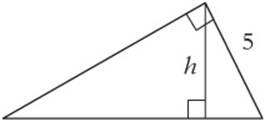
Example:
In the figure below, what is x?

You can also use the modified Pythagorean theorem to find whether a triangle is acute or obtuse.
If (side1)2 + (side2)2 < (longest side)2, the triangle is obtuse. (If the stick gets bigger, the alligator”s mouth gets wider!)
If (side1)2 + (side2)2 > (longest side)2, the triangle is acute. (If the stick gets smaller, the alligator”s mouth gets smaller!)
Special Right Triangles
Certain special right triangles show up frequently on the SAT. If you see that a triangle fits one of these patterns, it may save you the trouble of using the Pythagorean Theorem. But be careful: you must know two of three “parts” of the triangle in order to assume the third part.
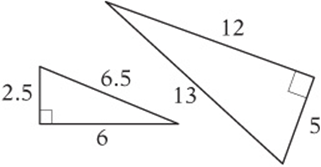
3-4-5 triangles More accurately, these can be called 3x-4x-5x triangles because the multiples of 3-4-5 also make right triangles. Notice that the sides satisfy the Pythagorean theorem.
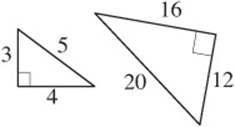
5-12-13 triangles Likewise, these can be called 5x-12x-13 x triangles because the multiples of 5-12-13 also make right triangles. Notice that the sides satisfy the Pythagorean theorem.
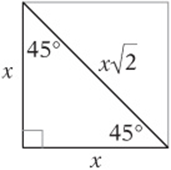
45°-45°-90°triangles These triangles can be thought of as squares cut on the diagonal. This shows why the angles and sides are related the way they are. Notice that the sides satisfy the Pythagorean theorem.
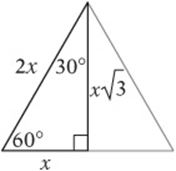
30°-60°-90°triangles These triangles can be thought of as equilateral triangles cut in half. This shows why the angles and sides are related the way they are. Notice that the sides satisfy the Pythagorean theorem.
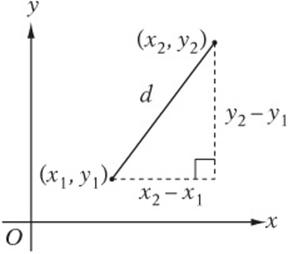
The Distance Formula
Say you want to find the distance between two points (x1, y1) and (x2, y2). Look carefully at this diagram and notice that you can find it with the Pythagorean theorem. Just think of the distance between the points as the hypotenuse of a right triangle, and the Pythagorean theorem becomes—lo and behold—the distance formula!
The Distance Formula:
![]()
so ![]()
Concept Review 3: The Pythagorean Theorem
1. Draw an example of each of the four “special” right triangles.
Use the modified Pythagorean theorem and the triangle inequality to find whether a triangle with the given side lengths is acute, obtuse, right, or impossible.
2. 5, 6, 9
3. 2, 12, 12
4. 6, 8, 11
5. 2, 2, 12
6. 3, 4, 7
7. 1.5, 2, 2.5
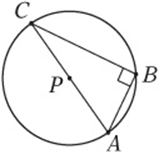
8. The circle above has its center at P and an area of 16π. If ![]() , what is the area of ΔABC? ____________
, what is the area of ΔABC? ____________

SAT Practice 3: The Pythagorean Theorem
1. The length and width of a rectangle are in the ratio of 5:12. If the rectangle has an area of 240 square centimeters, what is the length, in centimeters, of its diagonal?
(A) 26
(B) 28
(C) 30
(D) 32
(E) 34
2. A spider on a flat horizontal surface walks 10 inches east, then 6 inches south, then 4 inches west, then 2 inches south. At this point, how many inches is the spider from its starting point?
(A) 8
(B) 10
(C) 12
(D) 16
(E) 18
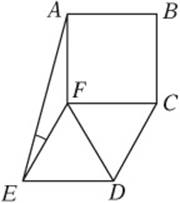
3. In the figure above, ABCF is a square and ΔEFD and ΔFCD are equilateral. What is the measure of ∠AEF?
(A) 15°
(B) 20°
(C) 25°
(D) 30°
(E) 35°
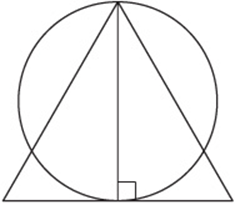
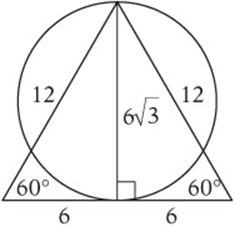
4. In the figure above, an equilateral triangle is drawn with an altitude that is also the diameter of the circle. If the perimeter of the triangle is 36, what is the circumference of the circle?
![]()
![]()
![]()
![]()
(E) 36π
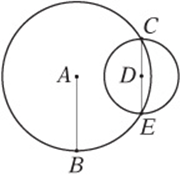
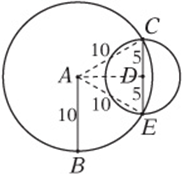
5. In the figure above, A and D are the centers of the two circles, which intersect at points C and E.![]() is a diameter of circle D. If
is a diameter of circle D. If ![]() , what is AD?
, what is AD?
(A) 5
![]()
![]()
![]()
![]()
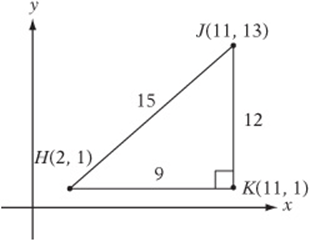
6. Point H has coordinates (2, 1), and point J has coordinates (11, 13). If ![]() is parallel to the x-axis and
is parallel to the x-axis and ![]() is parallel to the y-axis, what is the perimeter of ΔHJK?
is parallel to the y-axis, what is the perimeter of ΔHJK?

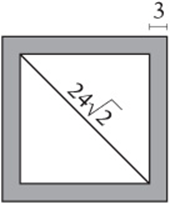
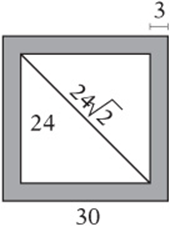
7. A square garden with a diagonal of length ![]() meters is surrounded by a walkway 3 meters wide. What is the area, in square meters, of the walkway?
meters is surrounded by a walkway 3 meters wide. What is the area, in square meters, of the walkway?

Note: Figure not drawn to scale.
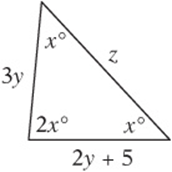
8. In the figure above, what is the value of z?
(A) 15
![]()
![]()
![]()
![]()
Answer Key 3: The Pythagorean Theorem
Concept Review 3
1. Your diagram should include one each of a ![]() ,
, ![]() , a
, a ![]() , and a 45°-45°-90° triangle.
, and a 45°-45°-90° triangle.
2. Obtuse: ![]()
3. Acute: ![]()
4. Obtuse: ![]()
5. Impossible: ![]() isn”t greater than 12
isn”t greater than 12
6. Impossible: ![]() isn”t greater than 7
isn”t greater than 7
7. Right: ![]()
8. Since the area of a circle is ![]() ,
, ![]() . Put the information into the diagram. Use the Pythagorean theorem or notice that, since the hypotenuse is twice the shorter side, it is a 30°-60° –90° triangle. Either way,
. Put the information into the diagram. Use the Pythagorean theorem or notice that, since the hypotenuse is twice the shorter side, it is a 30°-60° –90° triangle. Either way, ![]() , so the area of the triangle is
, so the area of the triangle is ![]() .
.
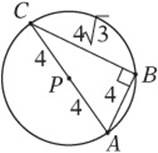
9. At first, consider the shorter leg as the base. In this case, the other leg is the height. Since the area is ![]() , the other leg must be 12. This is a 5-12-13 triangle, so the hypotenuse is 13. Now consider the hypotenuse as the base. Since
, the other leg must be 12. This is a 5-12-13 triangle, so the hypotenuse is 13. Now consider the hypotenuse as the base. Since ![]() ,
, ![]() .
.
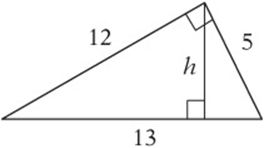
10. Your diagram should look like this: The height is ![]() .
.
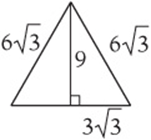
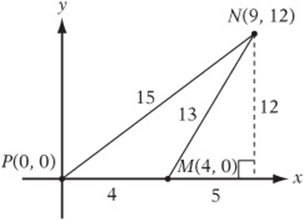
11. Sketch the diagram. Use the Pythagorean theorem or distance formula to find the lengths. The perimeter is ![]() .
.
SAT Practice 3
1. A Draw the rectangle. If the length and width are in the ratio of 5:12, then they can be expressed as 5x and 12x. The area, then, is ![]() . So
. So ![]() , and the length and width are 10 and 24. Find the diagonal with the Pythagorean theorem:
, and the length and width are 10 and 24. Find the diagonal with the Pythagorean theorem: ![]() , so
, so ![]() and
and ![]() . (Notice that this is a 5-12-13 triangle times 2!)
. (Notice that this is a 5-12-13 triangle times 2!)
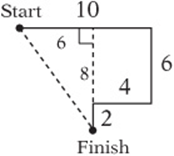
2. B Draw a diagram like this. The distance from the starting point to the finishing point is the hypotenuse of a right triangle with legs of 6 and 8. Therefore, the distance is found with Pythagoras: ![]() , so
, so ![]() . (Notice that this is a 3-4-5 triangle times 2!)
. (Notice that this is a 3-4-5 triangle times 2!)
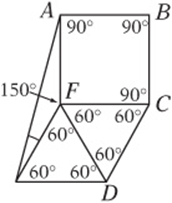
3. A Draw in the angle measures. All angles in a square are 90° and all angles in an equilateral triangle are 60°. Since all of the angles around point F add up to 360°, ![]() . Since
. Since ![]() ΔEFA is isosceles, so
ΔEFA is isosceles, so ![]() .
.
4. B If the perimeter of the triangle is 36, each side must have a length of 12. Since the altitude forms two 30°-60°-90° triangles, the altitude must have length ![]() This is also the diameter of the circle. The circumference of a circle is π times the diameter:
This is also the diameter of the circle. The circumference of a circle is π times the diameter:![]() .
.
5. C Draw in AE and AC. Since all radii of a circle are equal, their measures are both 10 as well. Therefore ΔACE is equilateral, and AD divides it into two 30°-60°-90° triangles. You can use the Pythagorean theorem, or just use the 30°-60°-90° relationships to see that ![]() .
.
6. 36 Sketch a diagram. Point K has coordinates (11, 1). ΔHJK is a right triangle, so it satisfies the Pythagorean theorem. Your diagram should look like this one. The perimeter is ![]() .
.
7. 324 Since the garden is a square, the diagonal divides it into 45°-45°-90° triangles. Therefore the sides have a length of 24. The outer edge of the walkway is therefore ![]() . The area of the walkway is the difference of the areas of the squares:
. The area of the walkway is the difference of the areas of the squares: ![]() .
.
8. B The sum of the angles is 180°, so ![]() , and
, and ![]() . Therefore the triangle is a 45°-45°-90° triangle. Since it is isosceles,
. Therefore the triangle is a 45°-45°-90° triangle. Since it is isosceles, ![]() , and therefore
, and therefore ![]() . The three sides, then, have lengths of 15, 15, and
. The three sides, then, have lengths of 15, 15, and ![]() .
.