SAT Test Prep

CHAPTER 10
ESSENTIAL GEOMETRY SKILLS

Lesson 6: Similar Figures

Similar Figures

When you think of similar you probably think of “almost the same, but not quite.” In mathematics, however, the word similar has a much more specific, technical meaning. Two figures are similar if they are the same shape, but not necessarily the same size. For instance, all circles are similar to each other, and all squares are similar to each other: there is only one “shape” for a circle, and only one “shape” for a square. But there are many different shapes that a rectangle may have, so two rectangles aren”t necessarily similar.

If two shapes are similar, then all corresponding angles are equal and all corresponding lengths are proportional.

Use proportions to find the lengths of unknown sides in similar figures.

Example:

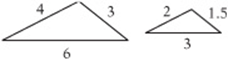
What is x in the figure at left below?

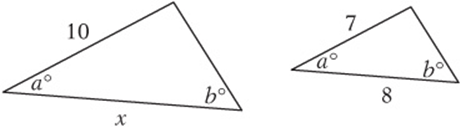
The two triangles are similar because all of their corresponding angles are equal. (Even though only two pairs of angles are given as equal, we know that the other pair are also equal, because the angles in a triangle must add up to 180°.) So we can set up a proportion of corresponding sides:

Two triangles are similar if any of the following is true:

• Two pairs of corresponding angles are equal. (If two pairs are equal, the third pair must be equal, too.)

• Two pairs of corresponding sides are proportional and the angles between them are equal.

• All three pairs of corresponding sides are proportional.

Ratios of Areas

Consider two squares: one with a side length of 2 and the other with a side length of 3. Clearly, their sides are in the ratio of 2:3. What about their areas? That”s easy: their areas are and , so the areas are in a ratio of 4:9. This demonstrates a fact that is true of all similar figures:

If corresponding lengths of two similar figures have a ratio of a:b, then the areas of the two figures have a ratio of a²:b².

Example:

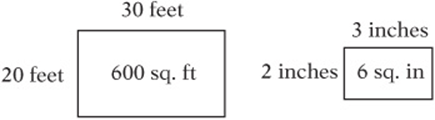
A garden that is 30 feet long has an area of 600 square feet. A blueprint of the garden that is drawn to scale depicts the garden as being 3 inches long. What is the area of the blueprint drawing of the garden?

It is tempting to want to say 60 square inches because . But be careful: the ratio of areas is the square of the ratio of lengths! You can draw a diagram, assuming the garden to be a rectangle. (The shape of the garden doesn”t matter: it”s convenient to draw the garden as a rectangle, but it doesn”t have to be.) Or you can simply set up the proportion using the formula: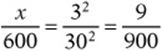

Concept Review 6: Similar Figures

1. If two figures are similar, then their corresponding sides are ____________________ and their corresponding angles are ____________________.

2. What are the three sets of conditions of which any one is sufficient to show that two triangles are similar?

a.

b.

c.

3. The hypotenuses of two similar right triangles are 4 centimeters and 6 centimeters long, respectively. If the area of the larger triangle is 27, what is the area of the smaller one?

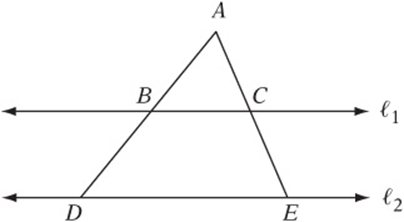
Note: Figure not drawn to scale.

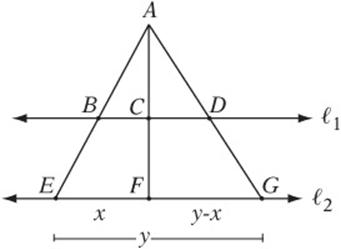
4. In the figure above, ℓ₁||ⅷ₂, , , and . What is the length of DE?

5. In a 5- × 8-inch rectangular photograph, the image of a tree is 3 inches high. The photograph is then magnified until its area is 1,000 square inches. What is the height of the tree image in the larger photograph?

SAT Practice 6: Similar Figures

1. The ratio of the areas of two squares is 4:1. If the perimeter of the smaller square is 20, what is the perimeter of the larger square?

(A) 5

(B) 10

(C) 20

(D) 40

(E) 80

2. A scale drawing of a rectangular patio measures 5 centimeters by 7 centimeters. If the longer side of the actual patio is 21 feet, what is the area, in square feet, of the actual patio?

(A) 72

(B) 315

(C) 356

(D) 441

(E) 617

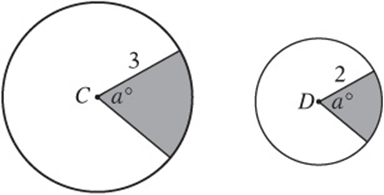
Note: Figure not drawn to scale.

3. In the figure above, C and D are the centers of the two circles with radii of 3 and 2, respectively. If the larger shaded region has an area of 9, what is the area of the smaller shaded region?

(A) 4

(B) 5

(C) 6

(D) 7

(E) 8

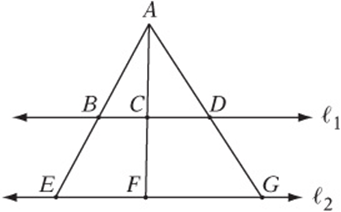
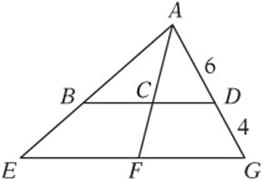
4. In the figure above, ℓ₁||ℓ₂. If , and , then which of the following represents the ratio of CD to BC?

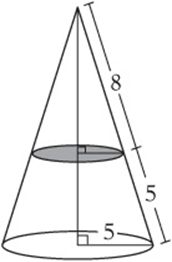
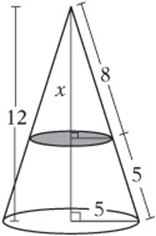
5. A circular cone with a base of radius 5 has been cut as shown in the figure above. What is the height of the smaller cone?

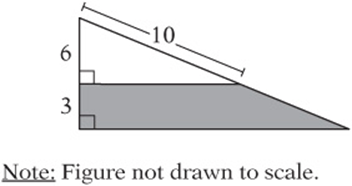
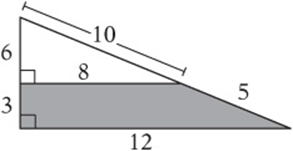
6. In the figure above, what is the perimeter of the shaded trapezoid?

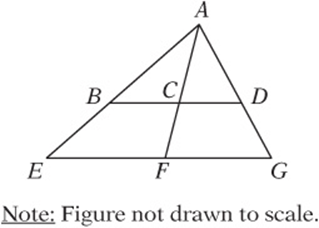
7. In the figure above, is parallel to , , , and ΔAEF has an area of 75. What is the area of ΔABC?

(A) 27

(B) 36

(C) 45

(D) 54

(E) 63

Answer Key 6: Similar Figures

Concept Review 6

1. If two figures are similar, then their corresponding sides are proportional and their corresponding angles are equal (or congruent).

2. a. two pairs of corresponding angles are equal

b. two pairs of corresponding sides are proportional and the included angles are equal

c. all three pairs of corresponding sides are proportional

3. The ratio of the sides is 4:6 or 2:3. The ratio of the areas is the square of the ratio of sides, which is 4:9. If x is the area of the smaller triangle, then . Solving for x gives x = 12.

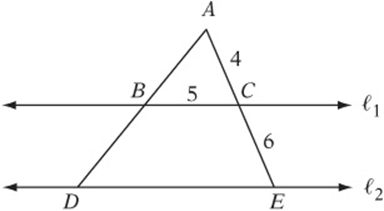
4. If ℓ₁ || ℓ₂, then the two triangles must be similar. Since corresponding sides are proportional, .

5. A 5- × 8-inch rectangle has an area of 40 square inches. The ratio of areas, then, is 40:1,000, or 1:25. This is the square of the ratio of lengths, so the ratio of lengths must be 1:5. If x is the length of the larger tree image, then . Cross-multiplying gives , so the tree is 15 inches high in the larger photograph.

SAT Practice 6

1. D If the ratio of the areas is 4:1, then the ratio of corresponding lengths is the square root: 2:1. If the perimeter of the smaller square is 20, then the perimeter of the larger one is twice as big.

2. B Find the width of the patio with a proportion:

So the patio is a 15- ×21-foot rectangle, which has an area of square feet.

3. A The two regions are similar, because the central angles are the same. The ratio of their corresponding lengths is 3:2, so the ratio of their areas is 9:4. Since the larger area is 9, the smaller area must be 4.

4. C If EF has length x and EG has length y, then FG must have length y = x, as shown. Since the two lines are parallel, ΔABC is similar to ΔAEF and ΔACD is similar to ΔAFG. Therefore and . So , and therefore .

5. B The height of the larger cone can be found with the Pythagorean theorem to be 12. (It”s the old 5-12-13 right triangle!) Since the two triangles are similar, . Multiplying by 12 gives .

6. 28 The two triangles are similar because their corresponding angles are equal. Since they are right triangles, the missing sides can be found with the Pythagorean theorem. Your diagram should look like the one above. The perimeter is .

7. A Since the lines are parallel, ΔABC is similar to ΔAEF and ΔACD is similar to ΔAFG. Therefore, . The ratio of areas between ΔABC and ΔAEF is the square of the ratio of sides, which is . Since ΔAEF has an area of 75, (the area of . So ΔABC has an area of 27.