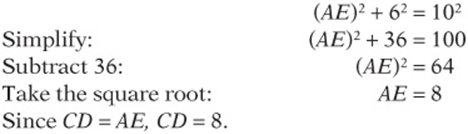SAT Test Prep

CHAPTER 10
ESSENTIAL GEOMETRY SKILLS

Lesson 8: Circles

Circle Basics

Okay, we all know a circle when we see one, but it often helps to know the mathematical definition of a circle.

• A circle is all of the points in a plane that are a certain distance r from the center.

• The radius is the distance from the center to any point on the circle.

Radius means ray in Latin; a radius comes from the center of the circle like a ray of light from the sun.

• The diameter is twice the radius:

Dia- means through in Latin, so the diameter is a segment that goes all the way through the circle.

The Circumference and Area

It”s easy to confuse the circumference formula with the area formula, because both formulas contain the same symbols arranged differently: circumference = 2πr and area = πr². There are two simple ways to avoid that mistake:

• Remember that the formulas for circumference and area are given in the reference information at the beginning of every math section.

• Remember that area is always measured in square units, so the area formula is the one with the “square: ” .

Tangents

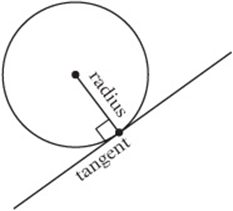
A tangent is a line that touches (or intersects) the circle at only one point. Think of a plate balancing on its side on a table: the table is like a tangent line to the plate.

A tangent line is always perpendicular to the radius drawn to the point of tangency.

Just think of a bicycle tire (the circle) on the road (the tangent): notice that the center of the wheel must be “directly above” where the tire touches the road, so the radius and tangent must be perpendicular.

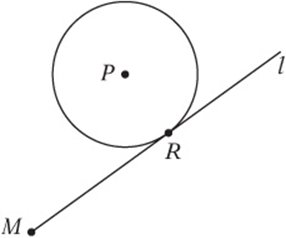
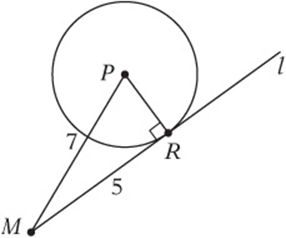
Example:

In the diagram above, point M is 7 units away from the center of circle P. If line l is tangent to the circle and , what is the area of the circle?

First, connect the dots. Draw MP and PR to make a triangle.

Since PR is a radius and MR is a tangent, they are perpendicular.

Since you know two sides of a right triangle, you can use the Pythagorean theorem to find the third

(PR)² is the radius squared. Since the area of the circle is πr², it is 24π.

Concept Review 8: Circles

1. What is the formula for the circumference of a circle?

2. What is the formula for the area of a circle?

3. What is a tangent line?

4. What is the relationship between a tangent to a circle and the radius to the point of tangency?

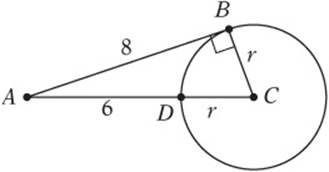
5. In the figure above, is a tangent to circle C, , and . What is the circumference of circle C?

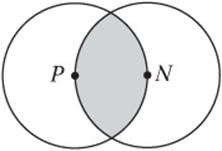
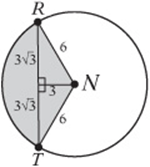
6. In the figure above, P and N are the centers of the circles and are 6 centimeters apart. What is the area of the shaded region?

SAT Practice 8: Circles

1. Two circles, A and B, lie in the same plane. If the center of circle B lies on circle A, then in how many points could circle A and circle B intersect?

I. 0

II. 1

III. 2

(A) I only

(B) III only

(C) I and III only

(D) I and III only

(E) I, II, and III

2. What is the area, in square centimeters, of a circle with a circumference of 16π centimeters?

(A) 8π

(B) 16π

(C) 32π

(D) 64π

(E) 256π

3. Point B lies 10 units from point A, which is the center of the circle of radius 6. If a tangent line is drawn from B to the circle, what is the distance from B to the point of tangency?

Note: Figure not drawn to scale.

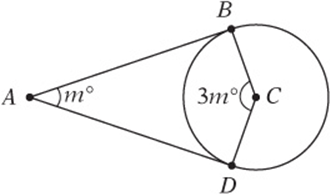
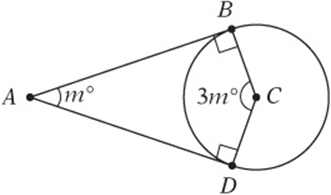
4. In the figure above, and are tangents to circle C. What is the value of m?

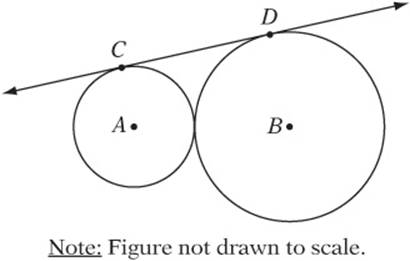
5. In the figure above, circle A intersects circle B in exactly one point, is tangent to both circles, circle A has a radius of 2, and circle B has a radius of 8. What is the length of ?

Answer Key 8: Circles

Concept Review 8

1. circumference = 2π r

3. A tangent line is a line that intersects a circle at only one point.

4. Any tangent to a circle is perpendicular to the radius drawn to the point of tangency.

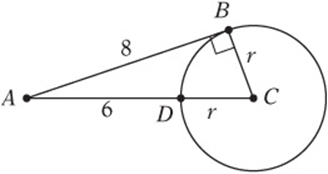
5. Draw to make a right triangle, and call the length of the radius r. Then you can use the Pythagorean theorem to find r:

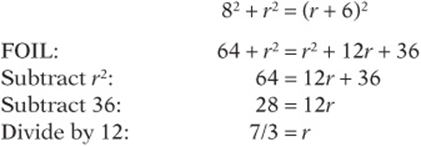
The circumference is 2πr, which is .

6. Draw the segments shown here. Since PN is a radius of both circles, the radii of both circles have the same length. Notice that PN, PR, RN, PT, and NT are all radii, so they are all the same length; thus, Δ PNT and ΔPRN are equilateral triangles and their angles are all 60° . Now you can find the area of the left half of the shaded region. This is the area of the sector minus the area of ΔRNT. Since ∠RNT is 120°, the sector is 120/360, or , of the circle. The circle has area 36°, so the sector has area 12π.ΔRNT consists of two 30°-60°-90° triangles, with sides as marked, so its area is . Therefore, half of the original shaded region is , and the whole is .

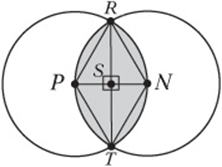
SAT Practice 8

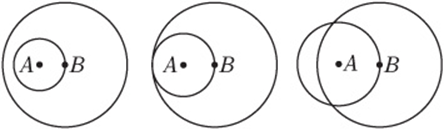
1. E The figure above demonstrates all three possibilities.

2. D The circumference . Dividing by 2π. gives . Area .

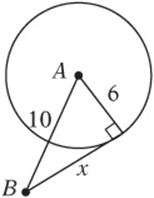
3. 8 Draw a figure as shown, including the tangent segment and the radius extended to the point of tangency. You can find x with the Pythagorean theorem:

4. 45 Since and are tangents to the circle, they are perpendicular to their respective radii, as shown. The sum of the angles in a quadrilateral is 360°, so m = 3m = 90 + 90 = 360 Simplify: 4m = 180 360 Subtract 180: 4m = 180 Divide by 4:m 45

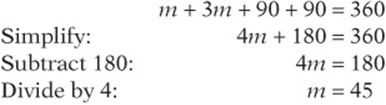
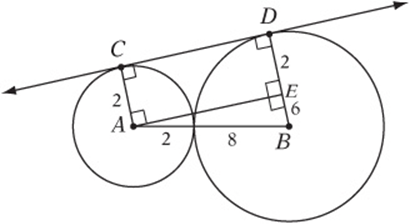
5. 8 Draw the segments shown. Choose point E to make rectangle ACDE and right triangle AEB. Notice that because opposite sides of a rectangle are equal. You can find AE with the Pythagorean theorem: