SAT 2016
CHAPTER 9
THE SAT MATH: ADVANCED MATHEMATICS
Skill 3: Working with Exponentials and Radicals
Lesson 9: The Laws of Exponentials
When working with exponentials you must understand the Laws of Exponentials.
Law #1: If n is a positive integer, then xn means the result when 1 is multiplied by x repeatedly n times.
e.g., 35 = 1 × 3 × 3 × 3 × 3 × 3 = 243
You might think that it”s unnecessary to include the 1 in this product, but including it will help clarify what zero, negative, and fractional exponents mean. For instance, think about the following sequence:
243, 81, 27, 9, 3, ___, ___, ___
What are the missing three terms in this sequence? With a little trial and error, you will see that the rule for getting each term is “divide the previous term by 3,” and therefore the missing terms are 1, 1/3, and 1/9. But notice, also, that these terms are just the descending integer powers of 3:

And so on. If you explore this pattern, and patterns for the powers of other numbers, you will notice that some other laws clearly emerge.
Law #2: As long as x does not equal 0, x0 =1.
You can think of x0 as meaning “1 multiplied by x zero times, or not at all.” Therefore, the result is 1.
Law #3: If n is a positive integer, then x–n means the result when 1 is divided by x repeatedly n times.
In other words, 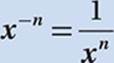 .
.
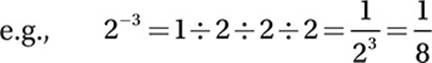
Law #4: xm × xn = xm + n (When multiplying exponentials with equal bases, add the exponents.)
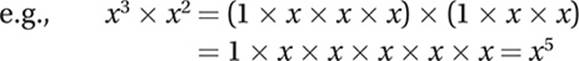
Law #5: xn × yn =(xy)n (When multiplying exponentials with equal exponents, multiply the bases.)
This law follows from the Commutative and Associative Laws of Addition.
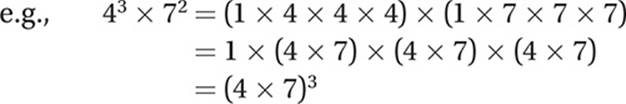
Law #6: 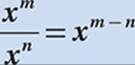 (When dividing exponentials with equal bases, subtract the exponents.)
(When dividing exponentials with equal bases, subtract the exponents.)
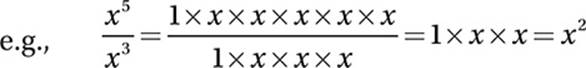
Law #7: 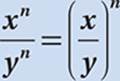 (When dividing exponentials with equal exponents, divide the bases.)
(When dividing exponentials with equal exponents, divide the bases.)
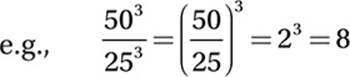
Law #8: (xm)n = xmn
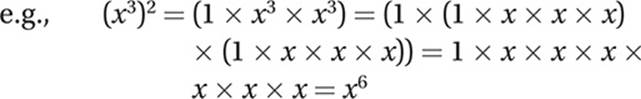
Law #9: ![]()
Proof: This follows directly from Law #8. If we raise ![]() to the nth power, by Law #8 we must get x1 or x. The number that we must raise to the nth power in order to get x is, by definition, the “nth root of x.”
to the nth power, by Law #8 we must get x1 or x. The number that we must raise to the nth power in order to get x is, by definition, the “nth root of x.”
Law #10: If x >1 and xa = xb, then a = b.
Which of the following expressions is equivalent to 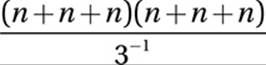 ?
?
A) ![]()
B) 3n2
C) 3n6
D) 27n2

Therefore, the correct answer is (D).
Which of the following expressions is equivalent to 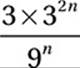 for all values of n?
for all values of n?
A) ![]()
B) 3
C) 3n
D) 92n

Therefore, the correct answer is (B).
Alternately, we can plug in various values for n and find that the expression gives a value of n no matter what.
Lesson 10: The Laws of Radicals
The radical symbol (![]() ) is used to indicate roots, which are the inverse of exponentials. For instance, because 23 = 8, we can say that 2 is the “third root” or “cube root” of 8 (
) is used to indicate roots, which are the inverse of exponentials. For instance, because 23 = 8, we can say that 2 is the “third root” or “cube root” of 8 (![]() ).
).
Law #9 of exponentials shows us that radicals (or “roots”) can be expressed as exponentials. For instance, ![]() . Therefore, we can use the Laws of Exponentials to simplify radical expressions.
. Therefore, we can use the Laws of Exponentials to simplify radical expressions.
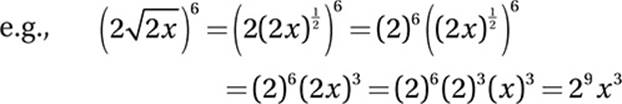
Law #1: ![]() (This is just the “reflected” version of Law of Exponentials #9.)
(This is just the “reflected” version of Law of Exponentials #9.)
Law #2: ![]() (This follows directly from Law of Exponentials #5.)
(This follows directly from Law of Exponentials #5.)
Law #3: 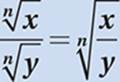 (This follows directly from Law of Exponentials #7.)
(This follows directly from Law of Exponentials #7.)
Working with square roots is much easier if you memorize the first 10 or so “perfect square integers”
22 = 4, 32 = 9, 42 = 16, 52 = 25, 62 = 36, 72 = 49,
82 = 64, 92 = 81, 102 = 100, 112 = 121, 122 = 144. . .
This will help you both simplify and estimate radical expressions.
• If the radicand has a perfect square factor, the radical can be simplified by factoring.
![]()
• If a fraction has a radical in the denominator, eliminate it by multiplying numerator and denominator by the radical.
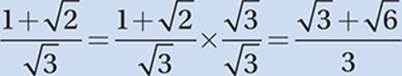
• To estimate the value of square roots, notice which two consecutive perfect squares the radicand lies between.
![]() and therefore
and therefore ![]()
Which of the following is equivalent to 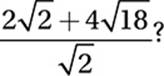 (No calculator)
(No calculator)
A) ![]()
B) 7
C) 14
D) 19
(Medium) Notice that each answer choice is much simpler than the original expression. This suggests that the original expression can be simplified. Let”s begin by looking at the radical expressions. If you know your perfect squares you will see that neither radicand (the expression inside the radical) is a perfect square, but one of the radicands—18—is a multiple of a perfect square: 18 = 2 × 9.
Original expression: 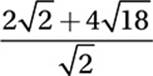
Substitute 18 = 9 × 2: 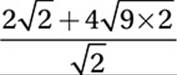
Apply Law #2: 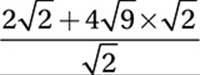
Simplify ![]() :
: 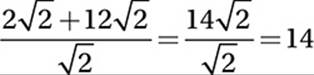
Therefore, the correct answer is (C).
If x2 = 4, y2 = 9, and (x – 2)(y + 3) ≠ 0, what is the value of x + y?
A) –5
B) –1
C) 1
D) 5
Every positive number has two distinct square roots. For instance, both 5 and –5 are the square root of 25, because (5)2 = 25 and (–5)2 = 25.
However, the symbol ![]() means the principal, or non-negative square root, so
means the principal, or non-negative square root, so ![]() and not –5.
and not –5.
(Easy) If x2 = 4, then x = ±2, and if y2 = 9, then y = ±2. But if (x – 2)(y + 3) ≠ 0, the x cannot equal 2 and y cannot equal –3. Therefore, x = –2 and y = 3, and x +y = 1, so the correct answer is (C).
Lesson 11: Solving radical and exponential equations
If 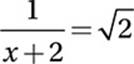 , what is the value of x?
, what is the value of x?
A) 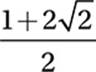
B) 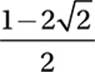
C) 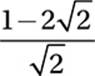
D) 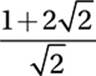
(Hard)
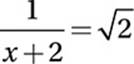
Multiply by (x + 2):
![]()
Distribute:
![]()
Subtract ![]() :
:
![]()
Divide by ![]() :
:
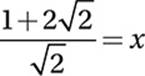
Therefore, the correct answer is (D).
If 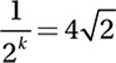 , what is the value of k?
, what is the value of k?
A) –3
B) ![]()
C) ![]()
D) ![]()
(Medium-hard)
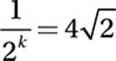
Use Exponential Law #3:
![]()
Use Radical Law #1:
![]()
Substitute 4 = 22:
![]()
Use Exponential Law #4:
![]()
If 2a = 2b, then a = b:
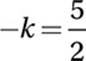
Multiply by –1:
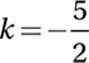
If 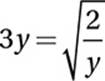 , what is the value of y3?
, what is the value of y3?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
(Hard)
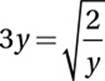
Use Radical Law #3:
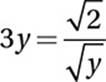
Multiply by ![]()
![]()
Use Radical Law #1:
![]()
Use Exponential Law #4:
![]()
Divide by 3:
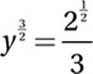
Square both sides:
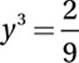
Therefore, the correct answer is (A).
Exercise Set 4 (No Calculator)
1
If 2a2 + 3a – 5a2 = 9, what is the value of a – a2?

2
If (200)(4,000) = 8 × 10m, what is the value of m?

3
If w = –1030, what is the value of 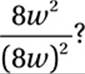

4
If 2x = 10, what is the value of 5(22x) + 2x?

5
If (x + 2)(x + 4)(x + 6) = 0, what is the greatest possible value of ![]()

6
If 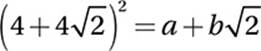 , where a and b are integers, what is the value of a +b?
, where a and b are integers, what is the value of a +b?

7
If 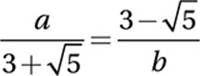 , what is the value of
, what is the value of 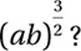 ?
?

8
If 9x = 25, what is the value of 3x–1?
A) ![]()
B) ![]()
C) ![]()
D) 24
9
If 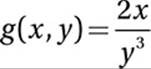 and a and b are positive numbers, what is the value of
and a and b are positive numbers, what is the value of 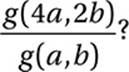
A) ![]()
B) ![]()
C) 2
D) 4
10
Which of the following is equivalent to 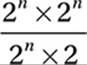 for all positive values of n?
for all positive values of n?
A) 2
B) 2n
C) 2n–1
D) 22n
11
Which of the following is equivalent to 3m + 3m + 3m for all positive values of m?
A) 3m+1
B) 32m
C) 33m
D) 33m+1
12
If x is a positive number and 5x = y, which of the following expresses 5y2 in terms of x?
A) 52x
B) 52x+1
C) 53x
D) 252x
Exercise Set 4 (Calculator)
13
If ![]() and n > 0, what is the value of n?
and n > 0, what is the value of n?

14
What is the smallest integer value of m such that 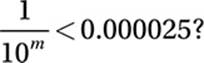

15
If 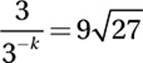 , what is the value of k?
, what is the value of k?

16
If (xm)3(xm + 1)2 = x37 for all values of x, what is the value of m?

17
If ![]() , what is the value of n?
, what is the value of n?

18
If 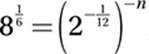 , what is the value of n?
, what is the value of n?

19
What is one possible value for x such that 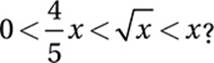

20
Which of the following is equivalent to 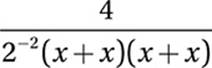 for all positive values of x?
for all positive values of x?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
21
The square root of a certain positive number is twice the number itself. What is the number?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
22
Which of the following is equivalent to 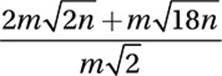 for all positive values of m and n?
for all positive values of m and n?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
23
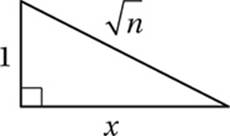
In the figure above, if n > 1, which of the following expresses x in terms of n?
A) ![]()
B) ![]()
C) ![]()
D) 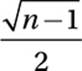
EXERCISE SET 4 ANSWER KEY
No Calculator
1. 3
2a2 + 3a – 5a2 = 9
Simplify:
3a – 3a2 = 9
Divide by 3:
a – a2 = 3
2. 5 (200)(4,000) = 800,000 = 8 × 105
3. 1/8 or .125
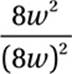
Exponential Law #5:
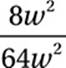
Cancel common factors:
![]()
4. 510
5(22x) + 2x
Exponential Law #8:
5(2x)2 + 2x
Substitute 2x = 10:
5(10)2 + 10
Simplify:
5(10)2 + 10 = 510
5. 64 If (x + 2)(x + 4)(x + 6) = 0, then x = –2, –4, or –6. Therefore 2–x could equal 22, 24, or 26. The greatest of these is 26 = 64.
6. 80
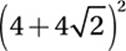
FOIL:
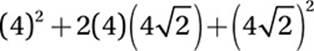
Simplify:
![]()
Simplify:
![]()
Therefore a = 48 and b = 32 and a + b = 80.
7. 8
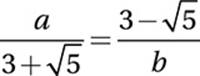
Cross-multiply:
![]()
Simplify:
ab = 9 – 5 = 4
Therefore ab3/2 = 43/2 = 8
8. 5/3 or 1.66 or 1.67
9x = 25
Substitute 9 = 32:
(32)x = 25
Exponential Law #8:
32x = 25
Take square root:
3x = 5
Divide by 3:
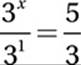
Exponential Law #6:
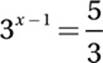
9. B
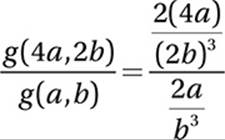
Simplify:
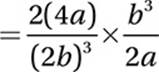
Simplify:
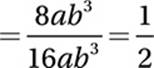
10. C
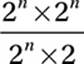
Cancel common factor:
![]()
Exponential Law #6:
2n - 1
11. A
3m + 3m + 3m
Combine like terms:
3(3m)
Exponential Law #4:
3m +1
12. B
5y2
Substitute y = 5x:
5(5x)2
Exponential Law #8:
5(52x)
Exponential Law #4:
52x+1
Calculator
13. 64
![]()
Radical Law #1
n2 = (644)1/2
Exponential Law #8:
n2 = 642
14. 5
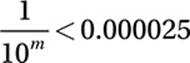
Scientific Notation:
1 × 10–m < 2.5 × 10–5
Substitution and checking makes it clear that m = 5 is the smallest integer that satisfies the inequality.
15. 2.5
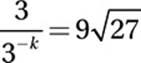
Exponential Law #6:
![]()
Simplify:
![]()
Express as exponentials:
![]()
Exponential Law #4:
3k+1 = 33.5
Exponential Law #10:
k + 1 = 3.5
Subtract 1:
k = 2.5
16. 7
(xm)3(xm+1)2 = x37
Exponential Law #8:
(x3m)(x2m+2) = x37
Exponential Law #4:
x5m +2 = x37
Exponential Law #10:
5m + 2 = 37
Subtract 2:
5m = 35
Divide by 5:
m = 7
17. 6
![]()
Factor:
![]()
Divide by ![]() :
:
![]()
Simplify:
18 – 12 = 6 = n
18. 6
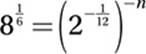
Substitute 8 = 23:
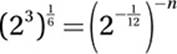
Exponential Law #8:
![]()
Exponential Law #10:
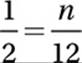
Multiply by 12:
6 = n
19. 1 < x ≤ 1.56
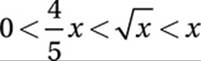
Middle inequality:
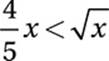
Square both sides:
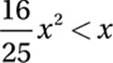
Divide by x:
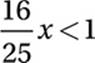
(Since x > 0, we do not “swap” the inequality.)
Multiply by 25/16:
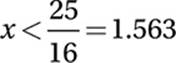
Last inequality:
![]()
Square both sides:
x < x2
Divide by x:
1 < x
Therefore, x must be both greater than 1 and less than or equal to 1.56.
20. B
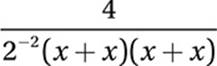
Simplify:
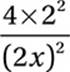
Simplify:
![]()
Cancel common factor:
![]()
21. B Translate:
![]()
Square both sides:
x = 4x2
Divide by x:
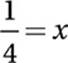
22. D
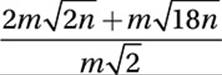
Factor terms:
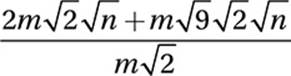
Cancel common factors:
![]()
Combine like terms:
![]()
23. B Pythagorean Theorem:
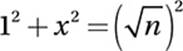
Simplify:
1 + x2 = n
Subtract 1:
x2 = n – 1
Take square root:
![]()