SAT 2016
CHAPTER 10
THE SAT MATH: ADDITIONAL TOPICS
Skill 3: Understanding Complex Numbers
Lesson 11: Understanding the imaginary number i and the complex plane
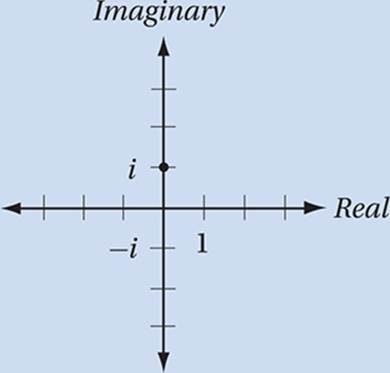
Imaginary Numbers
The imaginary number i is defined as the principal square root of –1.
The square root of a negative number is not on the real number line, because the square of a real number cannot be negative. Therefore, the square roots of negative numbers must reside on their own number line, which we call the “imaginary axis”, which is perpendicular to the real axis, intersecting it at the origin. The plane defined by the real axis and the imaginary axis is called the complex plane.
Given that 
, which of the following is equal to 
?
A) i
B) −i
C) 1
D) −1
(Medium-hard) To answer this question, we just need to know the basic exponent rules and the definition of i.
Original expression:
Factor:
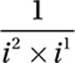
Substitute i2 = –1
Multiply by i/i:
Substitute i2 = –1:
–(–i) = i
Therefore, the correct answer is (A).
Lesson 12: Adding, multiplying, dividing, and simplifying complex numbers
Complex Numbers
The sum of a real number and an imaginary number is called a complex number. All complex numbers can be expressed in the form a + bi where a and b are real numbers and 
.
Every complex number a + bi corresponds to the point (a, b) on the complex plane.
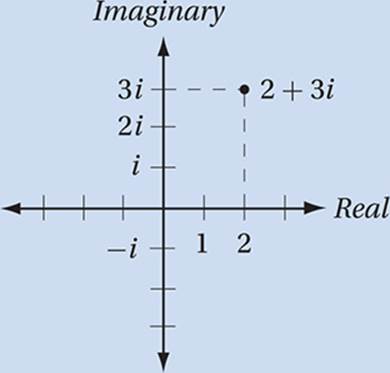
Adding Complex Numbers
To add complex numbers, just combine “like” terms.
Original expression:
(3 – 2i) + (2 + 6i)
Regroup with Commutative and Associative Laws of Addition:
(3 + 2) + (–2i + 6i)
Simplify:
5 + 4i
Multiplying Complex Numbers
To multiply complex numbers, just FOIL and combine like terms.
Original expression:
(3 – 2i)(2 + 6i)
FOIL:
(3)(2) + (3)(6i) + (–2i)(2) + (–2i)(6i)
Simplify:
6 + 18i – 4i –12i2
Substitute i2 = –1:
6 + 18i – 4i – 12(–1)
Combine like terms:
18 + 14i
Dividing Complex Numbers
To divide complex numbers, express the quotient as a fraction, multiply numerator and denominator by the complex conjugate of the denominator, and simplify. The complex conjugate of a + bi is a – bi.
Original expression:
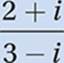
Multiply numerator and
denominator
by conjugate of denominator:
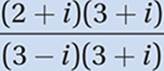
FOIL:
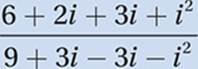
Simplify:
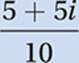
Distribute division:
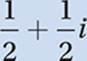
Powers of i
The successive powers of i (i1, i2, i3, i4, i5, i6, i7 . . .) cycle counterclockwise around the unit circle in the complex plane.
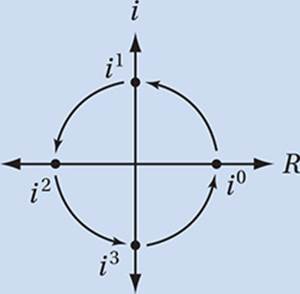
We can verify this by expanding any positive integer power of i.
Expression to be evaluated:
i13
Expand:
(i)(i)(i)(i)(i)(i)(i)(i)(i)(i)(i)(i)(i)
Group in pairs:
(i × i)(i × i)(i × i)(i × i)(i × i)(i × i)(i)
Substitute i2 = –1:
(–1)(–1)(–1)(–1)(–1)(–1)(i)
Simplify:
i
This implies that in = 1 if n is a multiple of 4. (That is, i4 = 1, i8 = 1, i12 = 1, etc.) This gives us a convenient way to simplify large powers of i: just replace the exponent with the remainder when it is divided by 4. For instance, i39 = i3 = –i, because 3 is the remainder when 39 is divided by 4.
If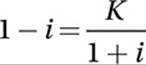 
, where 
, which of the following is equal to K2?
A) 2i
B) 4i
C) 4 + i
D) 4
Therefore, the correct answer is (D).
Which of the following is NOT equal to i6 – i2?
A) i5 – i
B) i4
C) 2i3 + 2i
D) 1 + i6
(Medium) Here, we have to use our knowledge about powers of i. Since i6 = (i × i)(i × i)(i × i) = (–1)(–1)(–1) = –1, and i2 = –1, the given expression, i6 – i2, is equal to (–1) – (–1) = 0. Simplifying each choice gives us
A) i5 – i = i – i = 0
B) i4 = 1
C) 2i3 + 2i = –2i + 2i = 0
D) 1 + i6 = 1 + (–1) = 0
Therefore, the correct answer is (B).
Exercise Set 4: Complex Numbers (No Calculator)
1
If a + bi = (1 + 2i)(3 – 4i), where a and b are constants and 
, what is the value of a + b?
2
If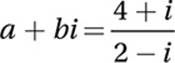 
, where a and b are constants and 
, what is the value of a?
3
For what value of b does (b + i)2 = 80 + 18i?
4
The solutions of the equation x2 – 2x + 15 = 0 are 
and 
, where a and b are positive numbers. What is the value of a + b?
5
Given that 
, which of the following is equal to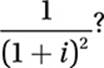 
?
A)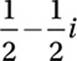 
B)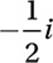 
C) 
D)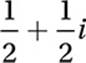 
6
Which of the following expressions is equal to (2 + 2i)2?
A) 0
B) 4i
C) 8i
D) 4 – 4i
7
If B(3 + i) = 3 – i, what is the value of B?
A)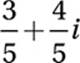 
B)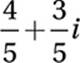 
C)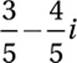 
D)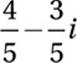 
8
x2 + kx = –6
If one of the solutions to the equation above is 
, what is the value of k?
A) –4
B) –2
C) 2
D) 4
9
If im = –i, which of the following CANNOT be the value of m?
A) 15
B) 18
C) 19
D) 27
EXERCISE SET 4: COMPLEX NUMBERS ANSWER KEY
No Calculator
1. 13
(1 + 2i)(3 – 4i)
FOIL:
(1)(3) + (1)(–4i) + (2i)(3) + (2i)(–4i)
Simplify:
3 – 4i + 6i – 8i2
Substitute i2 = –1:
3 – 4i + 6i –8(–1)
Combine like terms:
11 + 2i
Therefore, a = 11 and b = 2, so a + b = 13.
2. 7/5 or 1.4
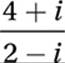
Multiply conjugate:
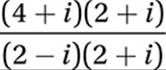
FOIL:
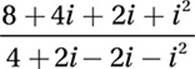
Substitute i2 = –1:
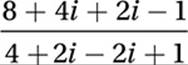
Combine like terms:
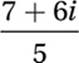
Distribute division:
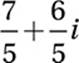
3. 9
(b + i)2
FOIL:
(b + i)(b + i) = b2 + bi + bi + i2
Substitute i2 = –1:
b2 + bi + bi – 1
Combine like terms:
(b2 – 1) + 2bi
Since this must equal 80 + 18i, we can find b by solving either b2 – 1 = 80 or 2b = 18. The solution to both equations is b = 9.
4. 15 The equation we are given is a quadratic equation in which a = 1, b = –2, and c = 15. Therefore, we can use the quadratic formula:
Quadratic Formula:
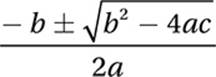
Substitute:
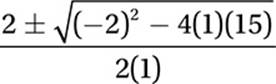
Simplify:
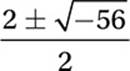
Simplify:
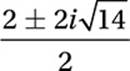
Distribute division:
Therefore, a = 1 and b = 14, so a + b = 15.
5. B
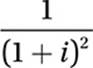
FOIL:
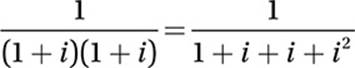
Substitute i2 = –1:
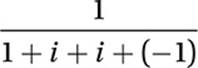
Simplify:
Multiply by i/i:
Substitute i2 = -1:
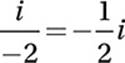
6. C
(2 + 2i)2
FOIL:
(2 + 2i)(2 + 2i) = 4 + 4i + 4i + 4i2
Substitute i2 = –1:
4 + 8i – 4 = 8i
7. D
B(3 + i) = 3 – i
Divide by 3 + i:
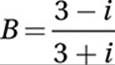
FOIL:
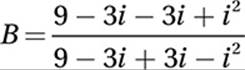
Substitute i2 = –1:
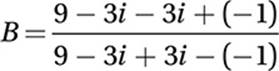
Simplify:
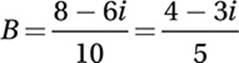
Distribute division:
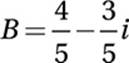
8. B
x2 + kx = –6
Add 6:
x2 + kx + 6 = 0
Substitute 
:
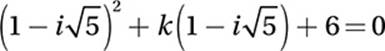
FOIL:
Simplify:
Distribute:
Collect terms:
Therefore, both 2 + k = 0 and 
. Solving either equation gives k = –2.
9. B As we discussed in Lesson 10, the powers of i are “cyclical,” and im = –i if and only if m is 3 more than a multiple of 4. The only number among the choices that is not 3 more than a multiple of 4 is (B) 18.