Cracking the New SAT with 4 Practice Tests, 2016 Edition (2015)

Part IV. How to Crack the Math Test

Chapter 11. Fun with Fundamentals

Although we’ll show you which mathematical concepts are most important to know for the SAT, this book relies on your knowledge of basic math concepts. If you’re a little rusty, this chapter is for you. Read on for a quick review of the math fundamentals you’ll need to know before you continue.

THE BUILDING BLOCKS

As you go through this book, you might discover that you’re having trouble with stuff you thought you already knew—like fractions or square roots. If this happens, it’s probably a good idea to review the fundamentals. That’s where this chapter comes in. Our drills and examples will refresh your memory if you’ve gotten rusty. Always keep in mind that the math tested on the SAT is different from the math taught in school. If you want to raise your score, don’t waste time studying math that ETS never tests.

Let’s talk first about what you should expect to see on the test.

THE MATH BREAKDOWN

The SAT includes two scored Math sections: Section 3 and Section 4. Section 3, which does not allow the use of a calculator, is 25 minutes long and includes 20 questions. Section 4, which allows the use of a calculator, is 55 minutes long and includes 38 questions.

According to ETS, the Math questions on the SAT fall into the following cleverly-named categories:

1.Heart of Algebra

2.Passport to Advanced Math

3.Problem Solving and Data Analysis

4.Additional Topics

No Need to Know

Here are a few things you
won’t need to know to
answer SAT math questions:
calculus, logarithms,
matrices, and geometric
proofs. Essentially, the
SAT tests a whole lot
of algebra and some
arithmetic, statistics, and
geometry.

The first three will give you some of your test subscores, but the names of all four categories don’t really mean anything. This is what will really be tested:

1.Algebra I and II

2.Arithmetic/Probability/Data Analysis

3.Plane Geometry/Coordinate Geometry/Trigonometry

That’s it! Of these categories, Algebra makes up the largest part of the test, accounting for more than half of the questions. Plane Geometry and Trigonometry make up the smallest part—there will only be a maximum of 6 questions from that category on the SAT.

The Math questions on your SAT will appear in two different formats:

1.Regular multiple-choice questions

2.Grid-Ins

The Grid-Ins will appear at the end of each Math section: 5 questions in Section 3, and 8 questions in Section 4. (See Chapter 17 for more on the Grid-In questions.)

THE INSTRUCTIONS

Both of the Math sections on the SAT will begin with the same set of instructions. We’ve reprinted these instructions, just as they appear on the SAT, in the Math sections of the practice tests in this book. These instructions include a few formulas and other information that you may need to know in order to answer some of the questions. You should learn these formulas ahead of time so you don’t have to waste valuable time flipping back to them during the test.

Still, if you do suddenly blank out on one of the formulas while taking the test, you can always refresh your memory by glancing back at the instructions. Be sure to familiarize yourself with them thoroughly ahead of time, so you’ll know which formulas are there.

STANDARD SYMBOLS

The following standard symbols are used frequently on the SAT:

THERE ARE ONLY SIX OPERATIONS

There are only six arithmetic operations that you will ever need to perform on the SAT:

1.Addition (3 + 3)

2.Subtraction (3 − 3)

3.Multiplication (3 × 3 or 3 • 3)

4.Division (3 ÷ 3 or 3/3)

5.Raising to a power (3³)

6.Finding a square root ()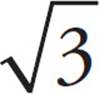

If you’re like most students, you probably haven’t paid much serious attention to these topics since junior high school. You’ll need to learn about them again if you want to do well on the SAT. By the time you take the test, using them should be automatic. All the arithmetic concepts are fairly basic, but you’ll have to know them cold. You’ll also have to know when and how to use your calculator, which will be quite helpful.

What Do You Get?

You should know the following arithmetic terms:

•The result of addition is a sum or total.

•The result of subtraction is a difference.

•The result of multiplication is a product.

•The result of division is a quotient.

•In the expression 5², the 2 is called an exponent.

The Six Operations Must Be Performed in the Proper Order

Very often, solving an equation on the SAT will require you to perform several different operations, one after another. These operations must be performed in the proper order. In general, the problems are written in such a way that you won’t have trouble deciding what comes first. In cases in which you are uncertain, you need to remember only the following sentence:

Please Excuse My Dear Aunt Sally;
she limps from left to right.

That’s PEMDAS, for short. It stands for Parentheses, Exponents, Multiplication, Division, Addition, and Subtraction. First, do any calculations inside the parentheses; then take care of the exponents; then perform all multiplication and division, from left to right, followed by addition and subtraction, from left to right.

The following drill will help you learn the order in which to perform the six operations. First, set up the equations on paper. Then, use your calculator for the arithmetic. Make sure you perform the operations in the correct order.

Do It Yourself

Some calculators
automatically take order
of operations into account,
and some don’t. Either
way, you can very easily
go wrong if you are in
the habit of punching
in long lines of arithmetic
operations. The safe,
smart way is to clear
the calculator after
every individual
operation, performing
PEMDAS yourself. When
calculator use is not
allowed, make sure to
write out all the steps
on your paper to avoid
careless errors.

DRILL 1

Solve each of the following problems by performing the indicated operations in the proper order. Answers can be found on this page.

1.107 + (109 − 107) =

2.(7 × 5) + 3 =

3.6 − 3(6 − 3) =

4.2 × [7 − (6 ÷ 3)] =

5.10 − (9 − 8 − 6) =

Whichever
Comes First

For addition and subtraction,
solve from left to
right. The same is true of
multiplication and
division. And remember:
If you don’t solve in
order from left to right,
you could end up with
the wrong answer!
Example:
24 ÷ 4 × 6 = 24 ÷ 24 = 1
wrong
24 ÷ 4 × 6 = 6 × 6 = 36
right

Parentheses Can Help You Solve Equations

Using parentheses to regroup information in SAT arithmetic problems can be very helpful. In order to do this, you need to understand a basic law that you have probably forgotten since the days when you last took arithmetic—the distributive law. You don’t need to remember the name of the law, but you do need to know how to use it to help you solve problems.

The Distributive Law

If you’re multiplying the sum of two numbers by a third number, you can multiply each number in your sum individually. This comes in handy when you have to multiply the sum of two variables.

If a problem gives you information in “factored form”—a(b + c)—then you should distribute the first variable before you do anything else. If you are given information that has already been distributed—(ab + ac)—then you should factor out the common term, putting the information back in factored form. Very often on the SAT, simply doing this will enable you to spot ETS’s answer.

Here are some examples:

Distributive: 6(53) + 6(47) = 6(53 + 47) = 6(100) = 600

Multiplication first: 6(53) + 6(47) = 318 + 282 = 600

You get the same answer each way, so why get involved with ugly arithmetic? If you use the distributive law for this problem, you don’t even need to use your calculator.

The drill on the following page illustrates the distributive law.

DRILL 2

Rewrite each problem by either distributing or factoring (Hint: For questions 1, 2, 4, and 5, try factoring) and then solve. Questions 3, 4, and 5 have no numbers in them; therefore, they can’t be solved with a calculator. Answers can be found on this page.

1.(6 × 57) + (6 × 13) = ____________

2.51(48) + 51(50) + 51(52) = ________

3.a(b + c − d) = _____________

4.xy − xz = _____________

5.abc + xyc = _____________

FRACTIONS

A Fraction Is Just Another Way of Expressing Division

The expression is exactly the same thing as x ÷ y. The expression means nothing more than 1 ÷ 2. In the fraction , x is known as the numerator (hereafter referred to as “the top”) and y is known as the denominator (hereafter referred to as “the bottom”).

Adding and Subtracting Fractions with the Same Bottom

To add two or more fractions that all have the same bottom, simply add the tops and put the sum over the common bottom. Consider the following example:

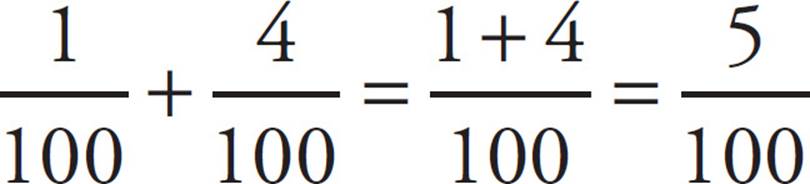
Subtraction works exactly the same way:

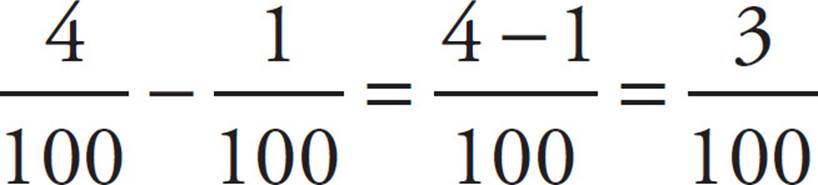
Fractions and Your Calculator

When calculator use is not allowed, be sure to write out all the steps on your paper to avoid careless errors. When calculator use is allowed, you can use your calculator to solve fraction problems. When you do, ALWAYS put each of your fractions in a set of parentheses. This will ensure that your calculator knows that they are fractions. Otherwise, the order of operations will get confused. On a scientific calculator, you can write the fraction in two different ways:

You will have a fraction key, which looks similar to “ 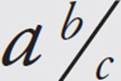.” If you wanted to write , you’d type “5 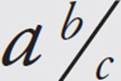6.”

You can also use the division key, because a fraction bar is the same as “divided by.” Be aware that your answer will be a decimal for this second way, so we recommend the first.

On a graphing calculator, you’ll use the division bar to create fractions. Keep in mind that, whatever calculator you are using, you can always turn your fractions into decimals before you perform calculations with them. Just be aware that the answer won’t always be exact.

Adding and Subtracting Fractions with Different Bottoms

In school you were taught to add and subtract fractions with different bottoms, or denominators, by finding a common bottom. To do this, you have to multiply each fraction by a number that makes all the bottoms the same. Most students find this process annoying.

Fortunately, we have an approach to adding and subtracting fractions with different bottoms that simplifies the entire process. Use the example below as a model. Just multiply in the direction of each arrow, and then either add or subtract across the top. Lastly, multiply across the bottom.

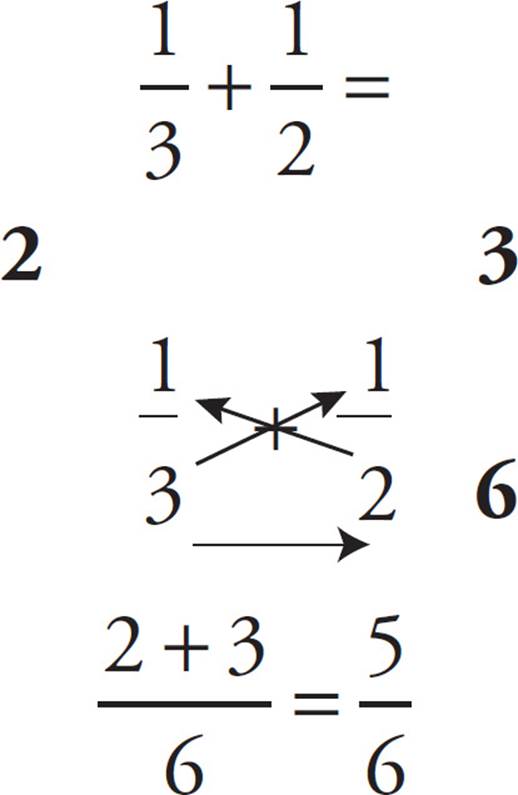
We call this procedure the Bowtie because the arrows make it look like a bowtie. Use the Bowtie to add or subtract any pair of fractions without thinking about the common bottom, just by following the steps above.

Calculating Fractions

Let’s say you wanted to find + = using your calculator. For a scientific calculator, you’d type in “(1 3) + (1 2) =” The answer will come up looking like something similar to 5 6, which means 5/6. On a graphing calculator, you’d type in (1/3) + (1/2) [ENTER]. This gives you the repeating decimal .833333. Now hit the [MATH] button and hit the [>FRAC] button and press [ENTER]. The calculator will now show “5/6.” The shortcut to turn a decimal into a fraction on a TI-80 series graphic calculator is [MATH][ENTER][ENTER]. Remember those parentheses for all fraction calculations!

Multiplying All Fractions

Multiplying fractions is easy. Just multiply across the top; then multiply across the bottom.

Here’s an example:

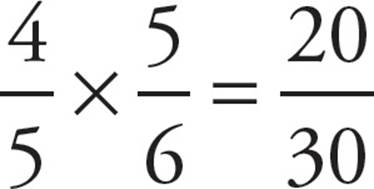
When you multiply fractions, all you are really doing is performing one multiplication problem on top of another.

You should never multiply two fractions before looking to see if you can reduce either or both. If you reduce first, your final answer will be in the form for which ETS is looking. Here’s another way to express this rule: Simplify before you multiply.

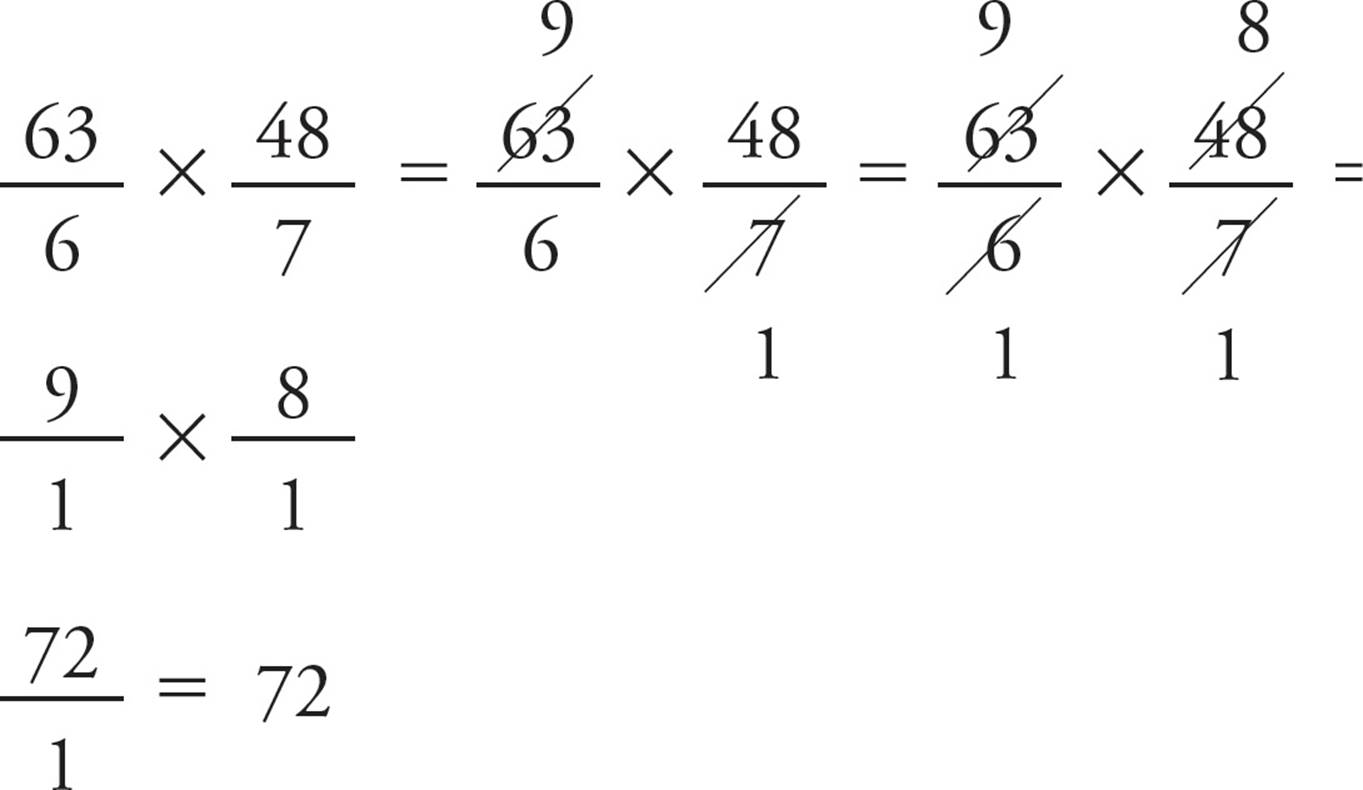
Dividing All Fractions

To divide one fraction by another, flip over (or invert) the second fraction and multiply.

Here’s an example:

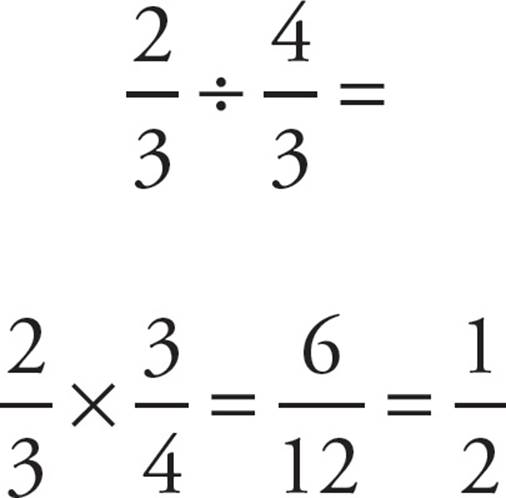
Just Flip It

Dividing by a fraction is
the same thing as multiplying
by the reciprocal of
that fraction. So just flip
over the fraction you
are dividing by and
multiply instead.

Be careful not to cancel or reduce until after you flip the second fraction. You can even do the same thing with fractions whose tops and/or bottoms are fractions. These problems look quite frightening but they’re actually easy if you keep your cool.

Here’s an example:

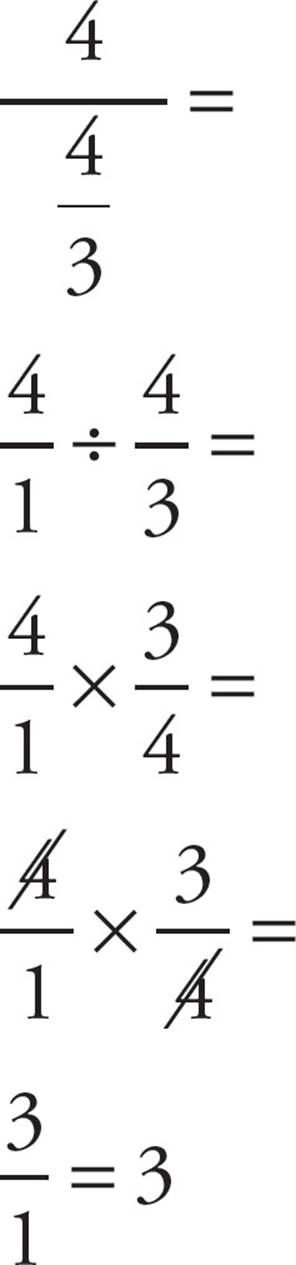
Reducing Fractions

When you add or multiply fractions, you will very often end up with a big fraction that is hard to work with. You can almost always reduce such a fraction into one that is easier to handle.

Start Small

It is not easy to see that
26 and 286 have a common
factor of 13, but it’s
pretty clear that they’re
both divisible by 2.
So start from there.

To reduce a fraction, divide both the top and the bottom by the largest number that is a factor of both. For example, to reduce 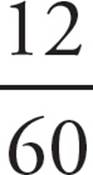, divide both the top and the bottom by 12, which is the largest number that is a factor of both. Dividing 12 by 12 yields 1; dividing 60 by 12 yields 5. The reduced fraction is .

If you can’t immediately find the largest number that is a factor of both, find any number that is a factor of both and divide both the top and bottom by that number. Your calculations will take a little longer, but you’ll end up in the same place. In the previous example, even if you don’t see that 12 is a factor of both 12 and 60, you can no doubt see that 6 is a factor of both. Dividing top and bottom by 6 yields 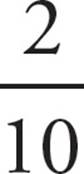. Now divide by 2. Doing so yields . Once again, you have arrived at ETS’s answer.

Fast Reduction

When calculator use is
allowed, reducing fractions
can be pretty easy. To
reduce fractions in your
scientific calculator, just
type in the fraction and hit
the equals key. If you are
using a graphing calculator,
type in the fraction, find
the [>FRAC] function, and
hit ENTER.

Converting Mixed Numbers to Fractions

A mixed number is a number such as 2. It is the sum of an integer and a fraction. When you see mixed numbers on the SAT, you should usually convert them to ordinary fractions.

Here’s a quick and easy way to convert mixed numbers.

•Multiply the integer by the bottom of the fraction.

•Add this product to the top of the fraction.

•Place this sum over the bottom of the fraction.

For practice, let’s convert 2 to a fraction. Multiply 2 (the integer part of the mixed number) by 4 (the bottom of the fraction). That gives you 8. Add that to the 3 (the top of the fraction) to get 11. Place 11 over 4 to get .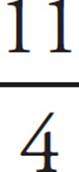

The mixed number 2 is exactly the same as the fraction 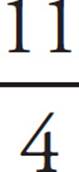. We converted the mixed number to a fraction because fractions are easier to work with than mixed numbers.

DRILL 3

Try converting the following mixed numbers. Answers can be found on this page.

1.8

2.2

3.5

4.2

5.6

Just Don’t Mix

For some reason, ETS
thinks it’s okay to give
you mixed numbers as
answer choices. On Grid-Ins,
however, if you use a
mixed number, ETS won’t
give you credit. You can
see why. In your Grid-In
box, 3¼ will be gridded
in as 31 / 4, which looks
like .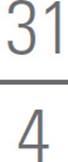

Fractions Behave in Peculiar Ways

Fractions don’t always behave the way you might want them to. For example, because 4 is obviously greater than 2, it’s easy to forget that is less than . It’s particularly confusing when the numerator is something other than 1. For example, is less than . Finally, you should keep in mind that when you multiply one fraction by another, you’ll get a fraction that is smaller than either of the first two. Study the following example:

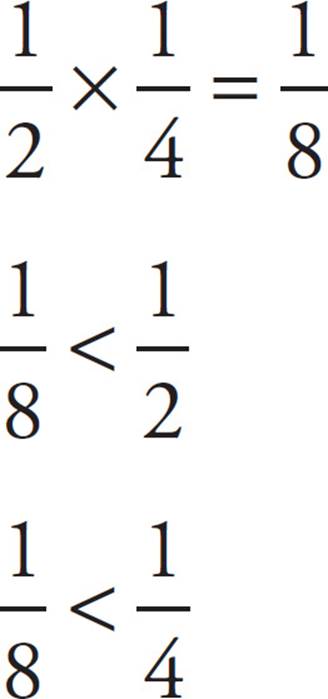
A Final Word About Fractions and Calculators

Throughout this section, we’ve given you some hints about your calculator and fractions. Of course, you still need to understand how to work with fractions the old-fashioned way for the No Calculator section. On the section in which its use is allowed, your calculator can be a tremendous help if you know how to use it properly. Make sure that you practice with your calculator so that working with fractions on it becomes second nature before the test.

DRILL 4

Work these problems with the techniques you’ve read about in this chapter so far. Then check your answers by solving them with your calculator. If you have any problems, go back and review the information just outlined. Answers can be found on this page.

Remember Your
Resources!

Check out the online
videos in your Premium
Portal for extra help with
test-taking strategies for
the Math Test.

1.Reduce .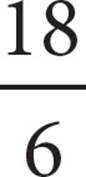

2.Convert 6 to a fraction.

3.2 − 3 =

4. × =

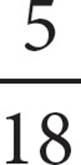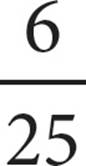5. ÷ =

6. =

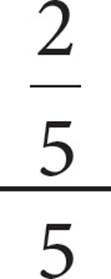7. =

DECIMALS

A Decimal Is Just Another Way of Expressing a Fraction

Fractions can be expressed as decimals. To find a fraction’s decimal equivalent, simply divide the top by the bottom. (You can do this easily with your calculator.)

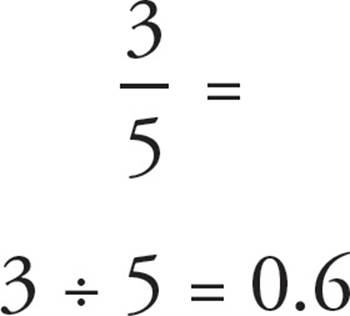
Adding, Subtracting, Multiplying, and Dividing Decimals

Manipulating decimals is easy with a calculator. Simply punch in the numbers—being especially careful to get the decimal point in the right place every single time—and read the result from the display. A calculator makes these operations easy. In fact, working with decimals is one area on the SAT where your calculator will prevent you from making careless errors. You won’t have to line up decimal points or remember what happens when you divide. The calculator will keep track of everything for you, as long as you punch in the correct numbers to begin with. Just be sure to practice carefully before test day.

What can you do when the math decimals get ugly on the No Calculator section? Never fear—you can still answer these questions. Just round the awkward numbers to ones that are easier to work with. As long as you aren’t rounding things too far, like rounding 33 to 50, the answers are likely to be spread far enough apart that only one or maybe two will be close to your estimated answer.

DRILL 5

Calculate each of the answers to the following questions on paper with your pencil, rounding any awkward numbers to make the math easier to handle. Then check your answers with your calculator. Answers can be found on this page.

1.0.43 × 0.87 =

2. =

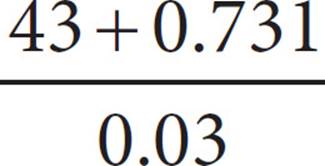3.3.72 ÷ 0.02 =

4.0.71 − 3.6 =

Comparing Decimals

Some SAT problems will ask you to determine whether one decimal is larger or smaller than another. Many students have trouble doing this. It isn’t difficult, though, and you will do fine as long as you remember to line up the decimal points and fill in missing zeros.

Place Value

Compare decimals
place by place, going
from left to right.

Here’s an example:

Problem: Which is larger, 0.0099 or 0.01?

Solution: Simply place one decimal over the other with the decimal points lined up, like this:

0.0099

0.01

To make the solution seem clearer, you can add two zeros to the right of 0.01. (You can always add zeros to the right of a decimal without changing its value.) Now you have this:

0.0099

0.0100

Which decimal is larger? Clearly, 0.0100 is, just as 100 is larger than 99. Remember that 0.0099 = 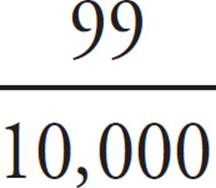, while 0.0100 = .

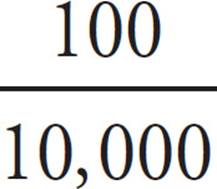Analysis

Watch out for problems like this with decimals in the answers. Any time you encounter a problem involving the comparison of decimals, be sure to stop and ask yourself whether you are about to make a careless mistake.

EXPONENTS AND SQUARE ROOTS

Exponents Are a Kind of Shorthand

Many numbers are the product of the same factor multiplied over and over again. For example, 32 = 2 × 2 × 2 × 2 × 2. Another way to write this would be 32 = 2⁵, or “thirty-two equals two to the fifth power.” The little number, or exponent, denotes the number of times that 2 is to be used as a factor. In the same way, 10³ = 10 × 10 × 10, or 1,000, or “ten to the third power,” or “ten cubed.” In this example, the 10 is called the base and the 3 is called the exponent. (You won’t need to know these terms on the SAT, but you will need to know them to follow our explanations.)

Exponents and Your Calculator

Raising a number to a power is shown in two different ways on your calculator, depending on the type of calculator you have. A scientific calculator will use the y^x button. You’ll have to type in your base number first, then hit the y^x key, and then type the exponent. So 4³ will be typed in as “4 y^x 3 =” and you’ll get 64. If you have a calculator from the TI-80 series, your button will be a ^ sign. You’ll enter the same problem as “4^3 [ENTER].” Think of these two keys as the “to the” button, because you say “4 to the 3rd power.”

Multiplying Numbers with Exponents

When you multiply two numbers with the same base, you simply add the exponents. For example, 2³ × 2⁵ = 2³⁺⁵ = 2⁸.

Warning

The rules for multiplying
and dividing exponents
do not apply to addition
or subtraction:
2² + 2³ = 12
(2 × 2) + (2 × 2 × 2) = 12
It does not equal 2⁵ or 32.

Dividing Numbers with Exponents

When you divide two numbers with the same base, you simply subtract the exponents. For example, 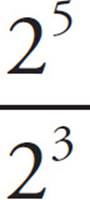= 2⁵⁻³ = 2².

Raising a Power to a Power

When you raise a power to a power, you multiply the exponents. For example, (2³)⁴ = 2^{3 × 4} = 2¹².

Warning

Parentheses are very
important with exponents,
because you must
remember to distribute
powers to everything
within them. For example,
(3x)² = 9x², not 3x².
Similarly, 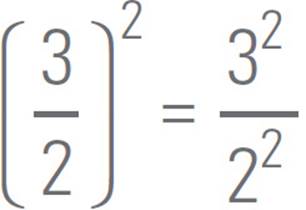, not
. But the distribution rule
applies only when you
multiply or divide. (x + y)² =
x² + 2xy + y², not x² + y².

MADSPM

To remember the exponent rules, all you need to do is remember the acronym MADSPM. Here’s what it stands for:

•Multiply → Add

•Divide → Subtract

•Power → Multiply

Whenever you see an exponent problem, you should think MADSPM. The three MADSPM rules are the only rules that apply to exponents.

Here’s a typical SAT exponent problem:

14For the equations 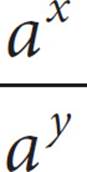= a¹⁰ and, (a^y)³ = a^x, if a > 1, what is the value of x ?

A)5

B)10

C)15

D)20

Here’s How to Crack It

This problem looks pretty intimidating with all those variables. In fact, you might be about to cry “POOD” and go on to the next problem. That might not be a bad idea but before you skip the question, pull out those MADSPM rules.

For the first equation, you can use the Divide-Subtract rule: 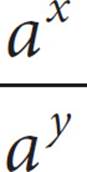= a^{x − y} = a¹⁰. In other words, the first equation tells you that x − y = 10.

For the second equation, you can use the Power-Multiply rule: (a^y)³ = a^3y = a^x. So, that means that 3y = x.

Now, it’s time to substitute: x − y = 3y − y = 10. So, 2y = 10 and y = 5. Be careful, though! Don’t choose (A). That’s the value of y, but the question wants to know the value of x. Since x = 3y, x = 3(5) = 15, which is (C).

If calculator use was allowed on this one, you could also do this question by plugging in the answer choices, or PITA, which will be discussed in more detail later in this book. Of course, you still need to know the MADSPM rules to do the question that way.

The Peculiar Behavior of Exponents

Raising a number to a power can have quite peculiar and unexpected results, depending on what sort of number you start out with. Here are some examples.

•If you square or cube a number greater than 1, it becomes larger. For example, 2³ = 8.

•If you square or cube a positive fraction smaller than one, it becomes smaller.

For example, .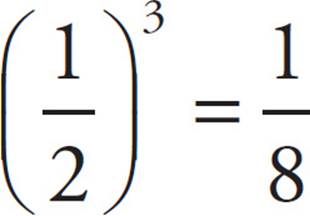

•A negative number raised to an even power becomes positive. For example, (−2)² = 4.

•A negative number raised to an odd power remains negative. For example, (−2)³ = −8.

You should also have a feel for relative sizes of exponential numbers without calculating them. For example, 2¹⁰ is much larger than 10². (2¹⁰ = 1,024; 10² = 100.) To take another example, 2⁵ is twice as large as 2⁴, even though 5 seems only a bit larger than 4.

See the Trap

ETS is hoping that you
won’t know these strange
facts about exponents,
so the test writers will
throw them in as trap
answers. Knowing the
peculiar behavior of
exponents will help you
avoid these tricky pitfalls
in a question.

Square Roots

The radical sign (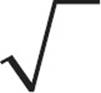) indicates the square root of a number. For example, 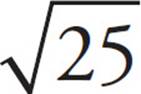= 5. Note that square roots cannot be negative. If ETS wants you to think about a negative solution, they’ll say x² = 25 because then x = 5 or x = −5.

The Only Rules You Need to Know

Here are the only rules regarding square roots that you need to know for the SAT:

1.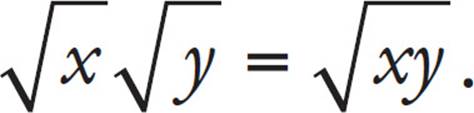 For example, .

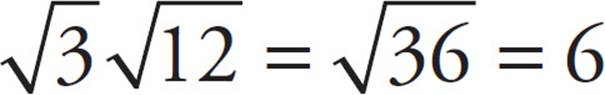2.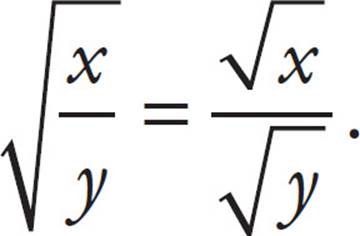 For example, .

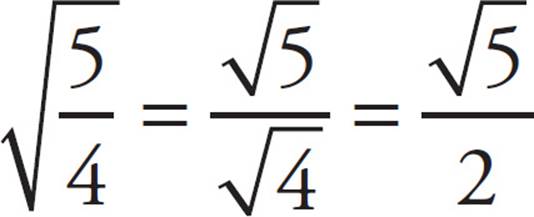3.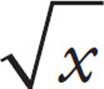 = positive root only. For example, 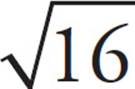= 4.

Note that rule 1 works in reverse: 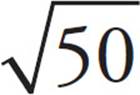= 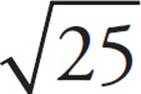× 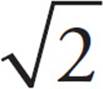= 5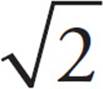. This is really a kind of factoring. You are using rule 1 to factor a large, clumsy radical into numbers that are easier to work with. Rule 2 works in reverse as well. divided by 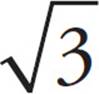looks ugly, but 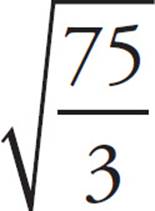= = 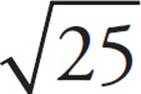5. And remember that radicals are just fractional exponents, so the same rules of distribution apply.

Roots and Your Calculator

Another important key is the root key. On a scientific calculator it is often the same button as y^x, but you’ll have to hit shift first. The symbol is 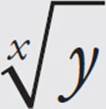. So “the 4th root of 81” would be “81 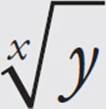4 = .” Sometimes the calculator will have y^x or 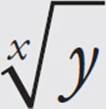as x^y or 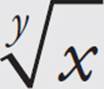. They mean the same thing. Just know which number you’re supposed to type in first.

The root key in the TI-80 graphing calculator series varies, but the most common symbol is the square root sign, which you can get to by pressing “[SHIFT] x².” In case you want to find the 3^rd, 4^th, or other root of a number, there is a button in the [MATH] directory f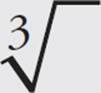or or 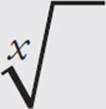. In the case of the 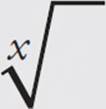, you have to type in the root you want, then hit [MATH] and , and finally hit your base number. For example, if you wanted to find the 4th root of 81, you’d type “4 [MATH],” then select , then type 81 and press [ENTER]. If you look at it on the screen, it will appear as “4 81,” which is similar to how you’d write it. You can also use the ^ symbol if you remember that a root is the same as the bottom part of a fractional exponent. So the fourth root of 81 would be written as “81 ^ (1/4)” on your calculator.

Careless Errors

Don’t make careless mistakes. Remember that the square root of a number between 0 and 1 is larger than the original number. For example, 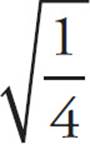= , and > .

Negative and Fractional Exponents

So far we’ve dealt with only positive integers for exponents, but they can be negative integers as well as fractions. The same concepts and rules apply, but the numbers just look a little weirder. Keep these concepts in mind:

•Negative exponents are a fancy way of writing reciprocals:

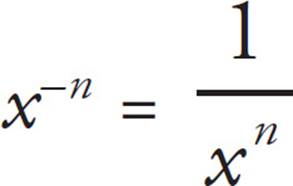
•Fractional exponents are a fancy way of taking roots and powers:

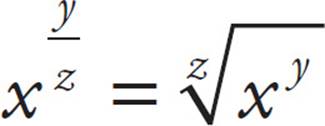
Here’s an example:

14.If x > 0, which of the following is equivalent to ?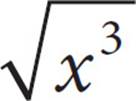

I.x +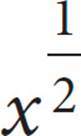

II.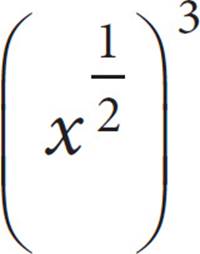

III.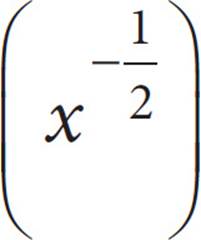

A)None

B)I and II only

C)II and III only

D)I, II, and III

Here’s How to Crack It

This problem really tests your knowledge of exponents. First, convert 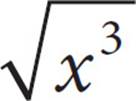into an exponent, since all of the Roman numerals contain expressions with exponents. (Plus, exponents are easier to work with because they have those nice MADSPM rules.) So, using the definition of a fractional exponent, 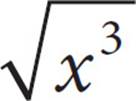= 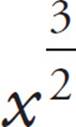. You want the items in the Roman numerals to equal .

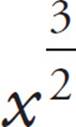Now, it’s time to start working with the Roman numerals. For (I), ETS is trying to be tricky. (There’s a surprise.) There’s no exponent rule for adding exponent expressions with like bases. So, x + 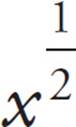does notequal 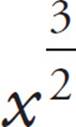. (If you want to be sure, you could try a number for x: If x = 4, then 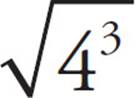= 8, but 4 + 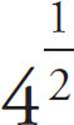= 4 + 2 = 6.) So, cross off any answer that includes (I): (B) and (D) are gone.

Now, since you are down to either (A) or (C), all you really need to do is try either (II) or (III). If either one works, the answer is (C). So, try (II). Use the power-multiply rule: 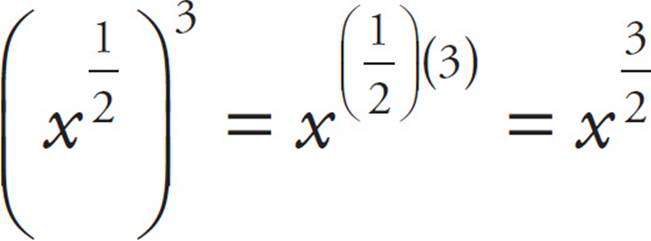. So, since (II) works, (C) is the correct answer. Notice that you didn’t even need to check (III). Using good POE on a Roman numeral question often means that you don’t need to check all the Roman numerals.

HOW TO READ CHARTS AND GRAPHS

Another basic math skill you will need for the SAT is the ability to interpret data from charts, graphs, tables, and more. This section will cover the basics of reading these figures. We will discuss how to answer questions related to charts and other figures in detail in Chapter 14.

More Math Basics

You can get more guidance
in the fundamentals of SAT
math and math strategies
by watching the videos
in your Premium Portal.
See “Register Your Book
Online!” for more
information.

What’s Up with All These Figures?

The SAT now includes charts, graphs, and tables throughout the test (not just in the Math sections) to present data for students to analyze. ETS believes this will better reflect what students learn in school and need to understand in the real world. The situations will typically include real-life applications, such as finance and business situations, social science issues, and scientific matter.

Since you’ll be seeing graphics throughout the test, let’s look at the types you may encounter and the skills you’ll need to be familiar with when you work with charts and graphs.

Types of Graphics

The Scatterplot

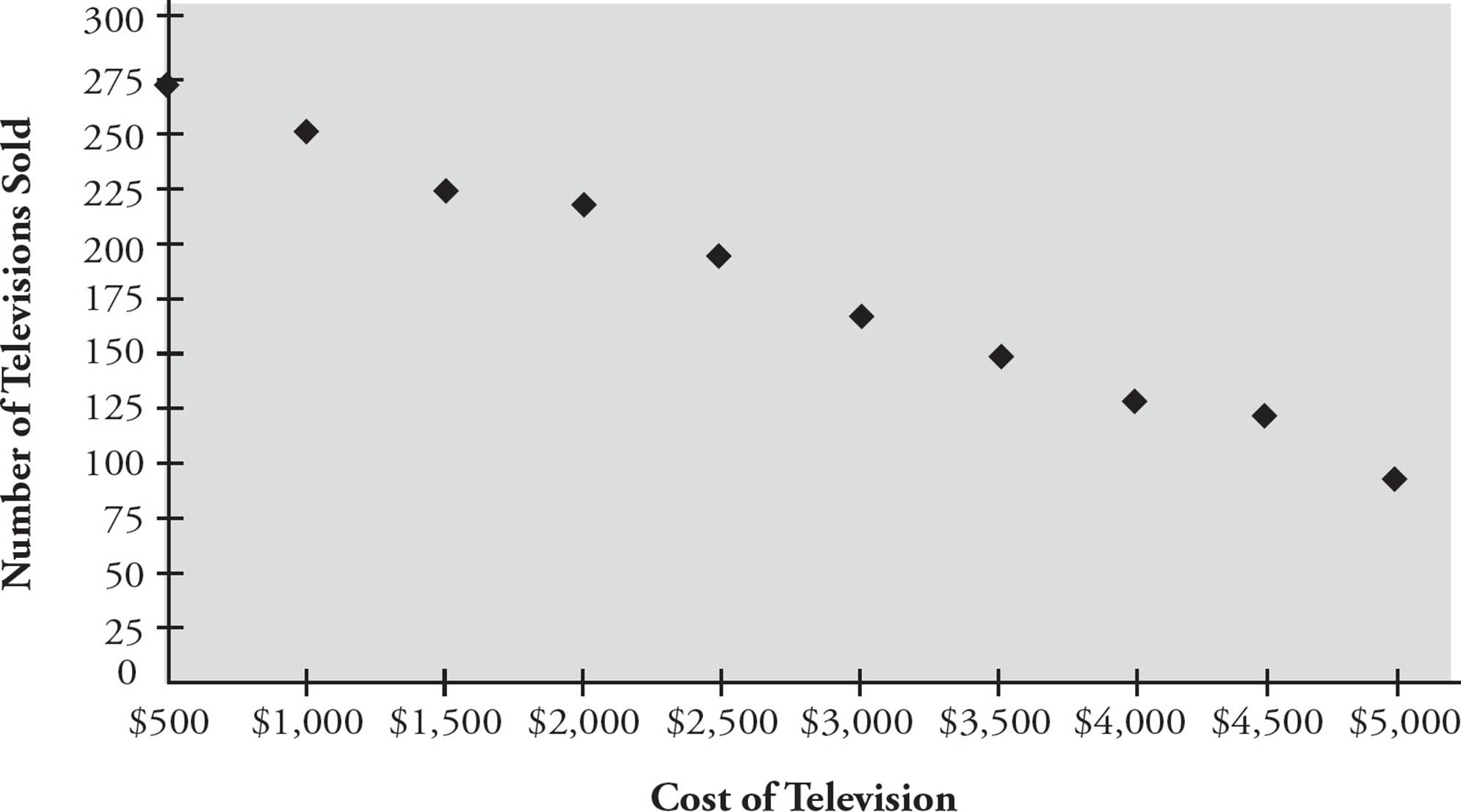
A scatterplot is a graph with distinct data points, each representing one piece of information. On the scatterplot below, each dot represents the number of televisions sold at a certain price point.

Here’s How to Read It

To find the cost of a television when 225 televisions are sold, start at 225 on the vertical axis and draw a horizontal line to the right until you hit a data point. Use the edge of your answer sheet as a straight-edge if you have trouble drawing your own straight lines. Once you hit a point, draw a straight line down from it to the horizontal axis and read the number the line hits, which should be $1,500. To determine the number of televisions sold when they cost a certain amount, reverse the steps—start at the bottom, draw up until you hit a point, then move left until you intersect the vertical axis.

Try the question now.

9.A certain store sells televisions ranging in price from $500 to $5,000 in increments of $500. The graph above shows the total number of televisions sold at each price during the last 12 months. Approximately how much more revenue did the store collect from the televisions it sold priced at $3,500 than it did from the televisions it sold priced at $1,000 ?

A)$175,000

B)$250,000

C)$275,000

D)$350,000

Here’s How to Crack It

The revenue is the cost of television × number of televisions sold. We need the information from the graph only for the television that costs $3,500 and for the television that costs $1,000 in order to determine how much more revenue the $3,500 television produced. There were 150 of the $3,500 televisions sold, for a revenue of $525,000. There were 250 of the $1,000 televisions sold, for a revenue of $250,000. The difference between the two is $525,000 − $250,000 = $275,000, as seen in (C).

A question may ask you to draw a “line of best fit” on a scatterplot diagram. This is the line that best represents the data. You can use the edge of your answer sheet as a ruler to help you draw a line that goes through most of the data.

The Line Graph

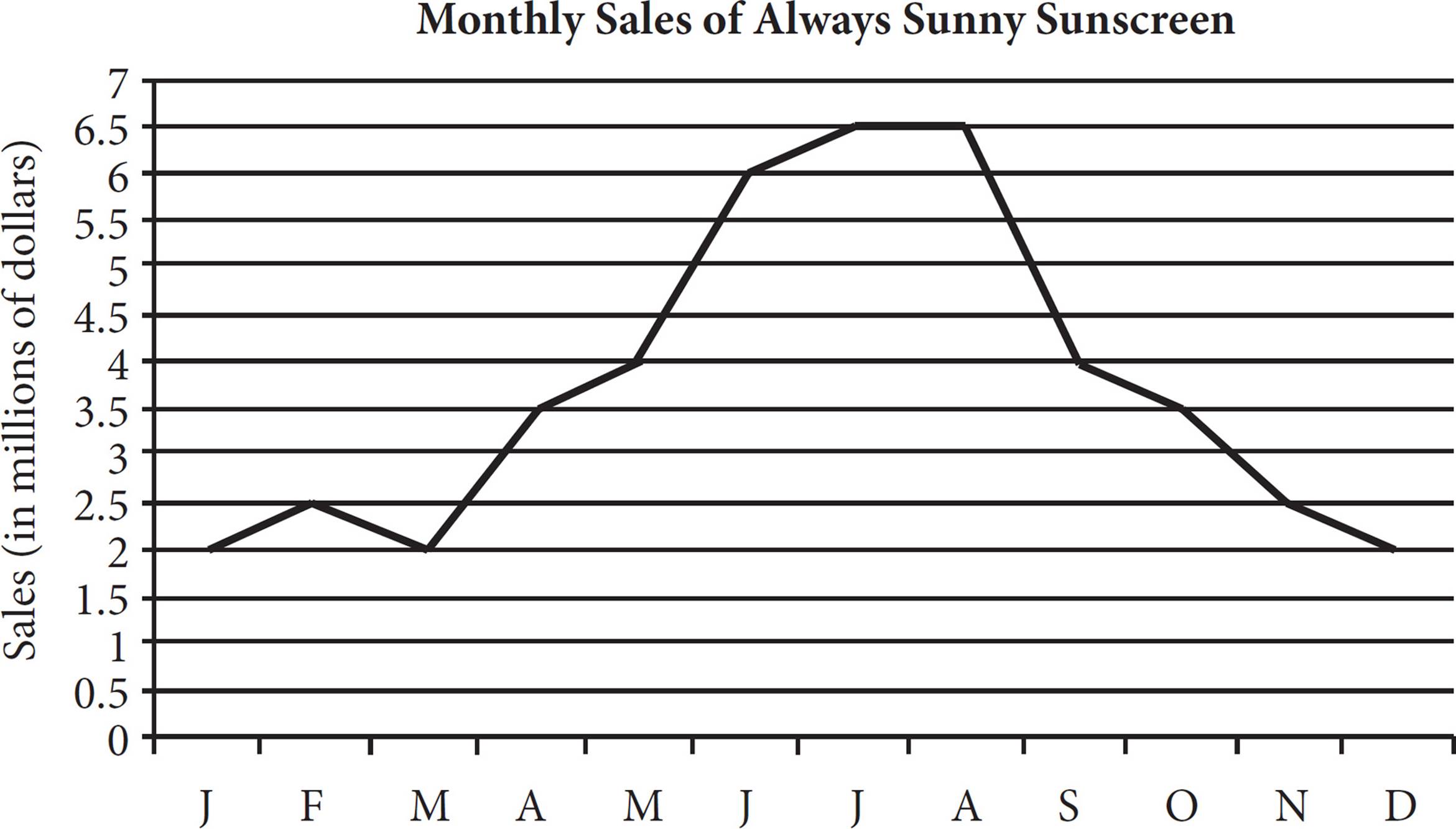
A line graph is similar to a scatterplot in that it shows different data points that relate the two variables. The difference with a line graph, though, is that the points have been connected to create a continuous line.

Here’s How to Read It

Reading a line graph is very similar to reading a scatterplot. Start at the axis that represents the data given, and draw a straight line up or to the right until you intersect the graph line. Then move left or down until you hit the other axis. For example, in February, indicated by an F on the horizontal axis, Always Sunny sunscreen had 2.5 million in sales. Make sure to notice the units on each axis. If February sales were only $2.50, rather than $2.5 million, then this company wouldn’t be doing very well!

Let’s look at a question about this line graph.

2.The forecasted monthly sales of Always Sunny Sunscreen are presented in the figure above. For which period are the forecasted monthly sales figures strictly decreasing then strictly increasing?

A)January to March

B)February to April

C)June to August

D)September to November

Here’s How to Crack It

Look up the values for each period in question and use Process of Elimination to get rid of those that don’t fit. For (A), January sales are forecasted to be $2 million, February $2.5 million, and March $2 million. This is an increase then a decrease, not the other way around, so eliminate (A). For (B), you already know sales decreased from February to March, so check for a following increase in April. The figure for April is $3.5 million, which is an increase over the March figure, so (B) is correct.

The Bar Graph (or Histogram)

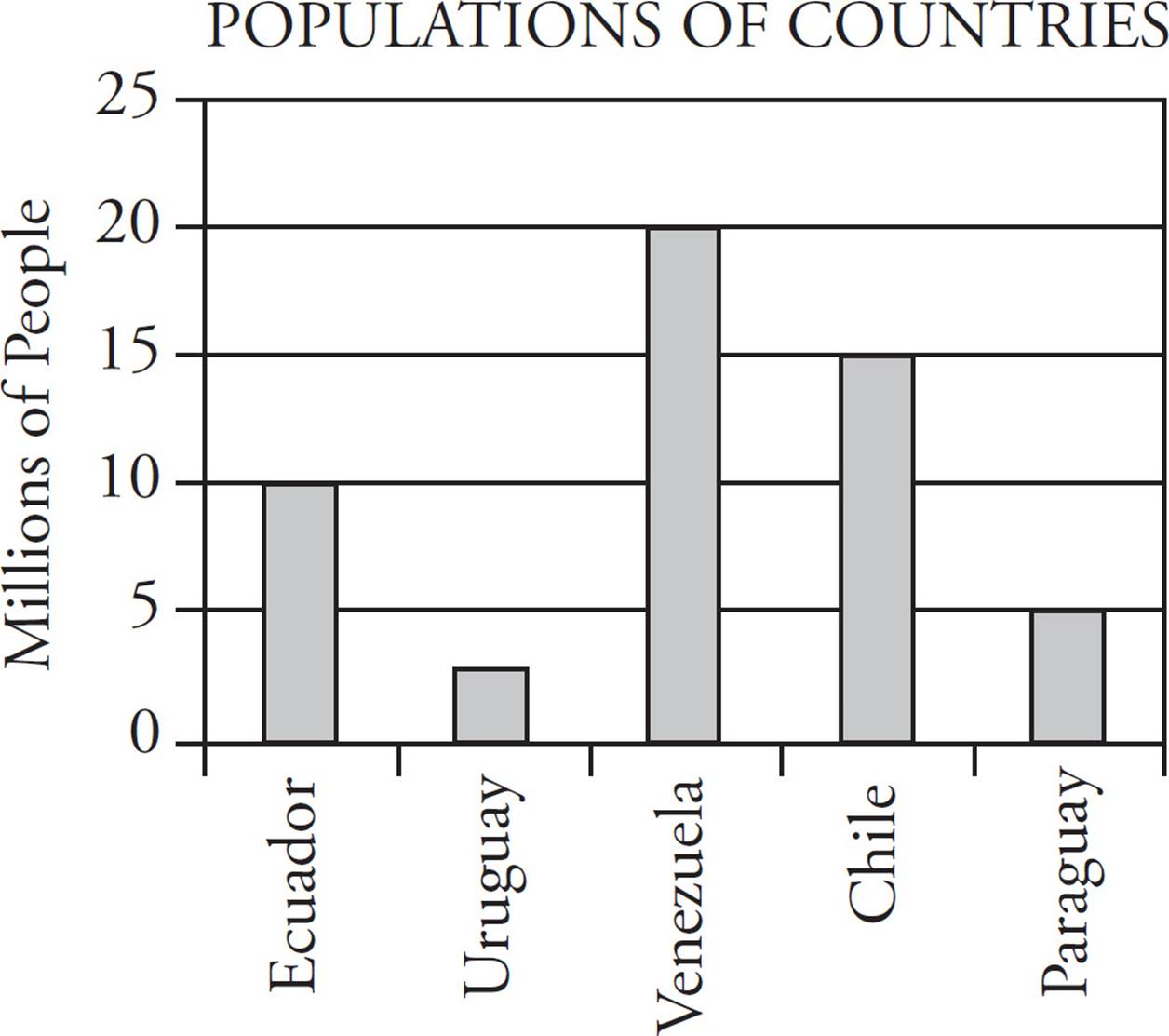
Instead of showing a variety of different data points, a bar graph will show how many items belong to a particular category. If the variable at the bottom is given in ranges, instead of distinct items, the graph is called a histogram, but you read it the same way.

Here’s How to Read It

The height of each bar corresponds to a value on the vertical axis. In this case, the bar above Chile hits the line that intersects with 15 on the vertical axis, so there are 15 million people in Chile. Again, watch the units to make sure you know what the numbers on the axes represent. On this graph, horizontal lines are drawn at 5 unit intervals, making the graph easier to read. If these lines do not appear on a bar graph, use your answer sheet to determine the height of a given bar.

A bar chart question might look like this:

14. The populations of five countries are shown in the graph above. If population density is defined as 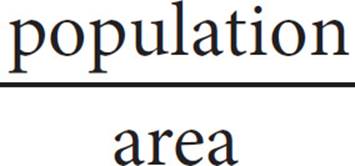, and the area of Paraguay is 400,000 square kilometers, what is the population density of Paraguay, in people per square kilometer?

A)0.08

B)0.8

C)1.25

D)12.5

Here’s How to Crack It

Start by determining the population of Paraguay. The bar hits right at the horizontal line for 5, which is in millions, so there are 5 million people in Paraguay. Now use the definition of population density in the question.

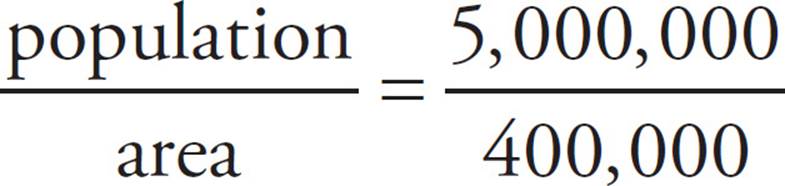
Be very careful with the number of zeroes you put in the fraction—the answer choices are pairs that vary by a factor of 10, meaning ETS expects you to miss a zero. The answer must be greater than 1, since your numerator is bigger than your denominator, so eliminate (A) and (B). Choice (C) also seems too small, but check the math on your calculator (carefully). You should get 12.5 people per square kilometer, so (D) is correct.

The Two-Way Table

A two-way table is another way to represent data without actually graphing it. Instead of having the variables represented on the vertical and horizontal axes, the data will be arranged in rows and columns. The top row will give the headings for each column, and the left-most column will give the headings for each row. The numbers in each box indicate the data for the category represented by the row and the column the box is in.

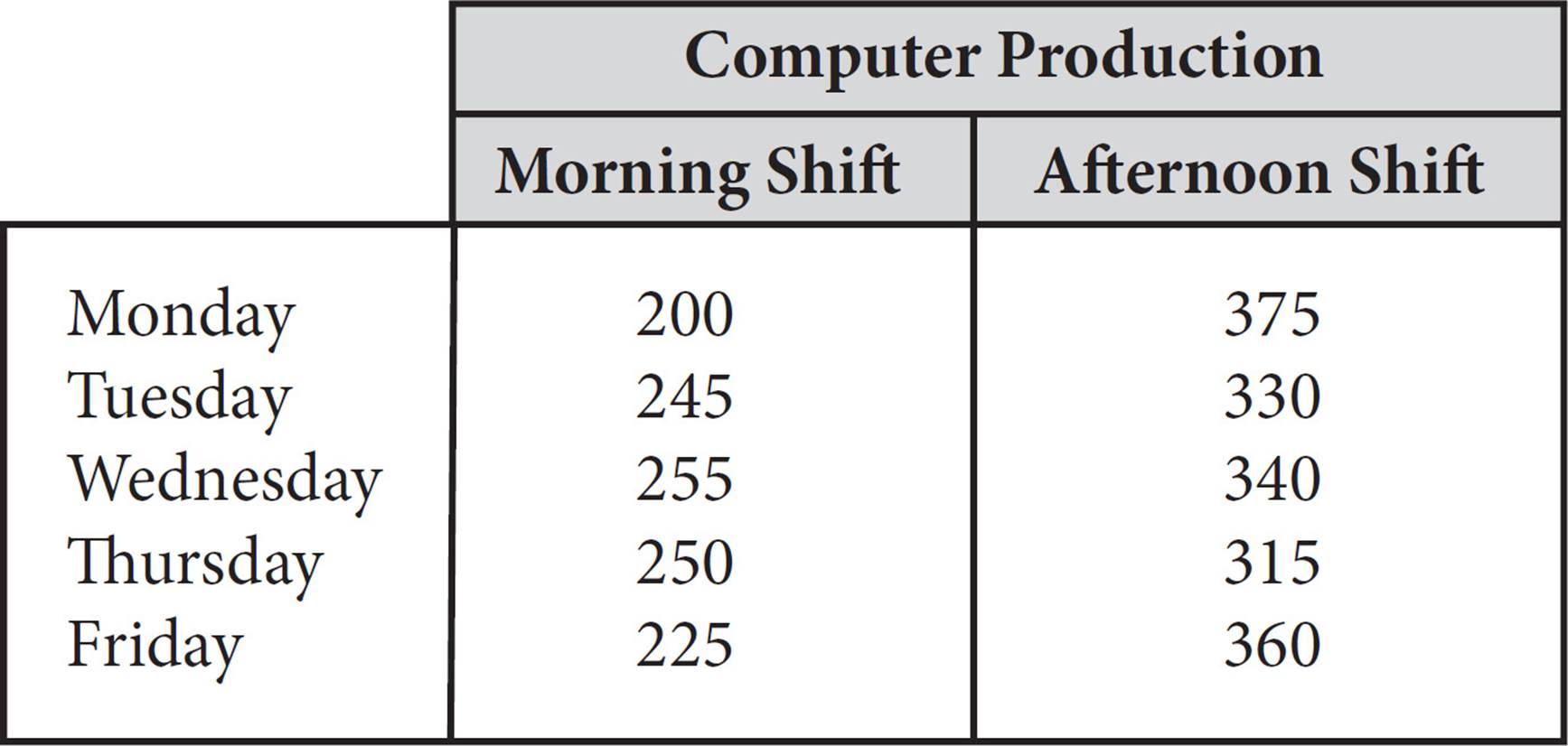
Here’s How to Read It

If you wanted to see the number of computers produced on Tuesday morning, you could start in the Morning Shift column and look down until you found the number in the row that says, “Tuesday,” or you could start in the row for Tuesday and look to the right until you found the Morning Shift column. Either way, the result is 245. Some tables will give you totals in the bottom row and/or the right-most column, but sometimes you will need to find the totals yourself by adding up all the numbers in each row or in each column. More complicated tables will have more categories listed in rows and/or columns, or the tables may even contain extraneous information.

Give this one a try.

3.Computer production at a factory occurs during two shifts, as shown in the chart above. If computers are produced only during the morning and afternoon shifts, on which of the following pairs of days is the greatest total number of computers produced?

A)Monday and Thursday

B)Tuesday and Thursday

C)Wednesday and Friday

D)Tuesday and Friday

Here’s How to Crack It

This is a perfect calculator question. Just add the morning shift and the afternoon shift for each day and see which total is the greatest. Write each total down next to the day on the chart, so you don’t have to keep track of it all in your head. Monday is 200 + 375 = 575, Tuesday is 245 + 330 = 575, Wednesday is 255 + 340 = 595, Thursday is 250 + 315 = 565, and Friday is 225 + 360 = 585. According to these calculations, Wednesday and Friday have the two greatest totals, so the greatest number of computers is produced on those two days together, making (C) the right answer.

Figure Facts

Every time you encounter a figure or graphic on the SAT, you should make sure you understand how to read it by checking the following things:

•What are the variables for each axis or the headings for the table?

•What units are used for each variable?

•Are there any key pieces of information (numbers, for example) in the legend of the chart that you should note?

•What type of relationship is shown by the data in the chart? For instance, if the chart includes curves that show an upward slope, then the graph shows a positive association, while curves that show a downward slope show a negative association.

•You can use the edge of your answer sheet as a ruler to help you make sure you are locating the correct data in the graph or to draw a line of best fit if necessary.

Fundamentals Drill 1: No Calculator Section

Work these Fundamentals questions without your calculator using the skills you’ve learned so far. Answers and explanations can be found on this page.

1.Which of the following represents the statement “the sum of the squares of x and y is equal to the square root of the difference of x and y”?

A)x² + y² =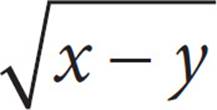

B)x² − y² =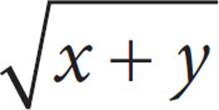

C)(x + y)² =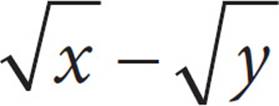

D)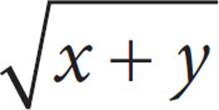 = (x − y)²

4.If a = −2, then a + a² − a³ + a⁴ − a⁵ =

A)−22

B)−18

C)32

D)58

6.If 9⁻² = 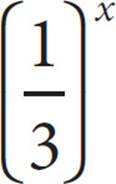^x, what is the value of x ?

A)1

B)2

C)4

D)6

7.

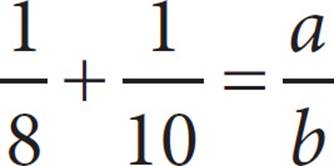
In the equation above, if a and b are positive integers and is in its simplest reduced form, what is the value of a ?

A)2

B)9

C)18

D)40

Fundamentals Drill 2: Calculator-Permitted Section

These Fundamentals questions are likely to appear in the section in which calculator use is allowed. Make sure to use it when you need to in order to avoid careless calculation errors. Don’t forget, though, that using it may slow you down when doing the math on paper would be faster. Answers and explanations can be found on this page.

1.If 7 times a number is 84, what is 4 times the number?

(A)16

(B)28

(C)48

(D)56

4.If 3x = 12, what is the value of ?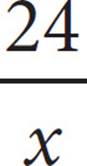

A)

B)

C)4

D)6

6.Which of the following graphs shows a strong positive association between x and y ?

A)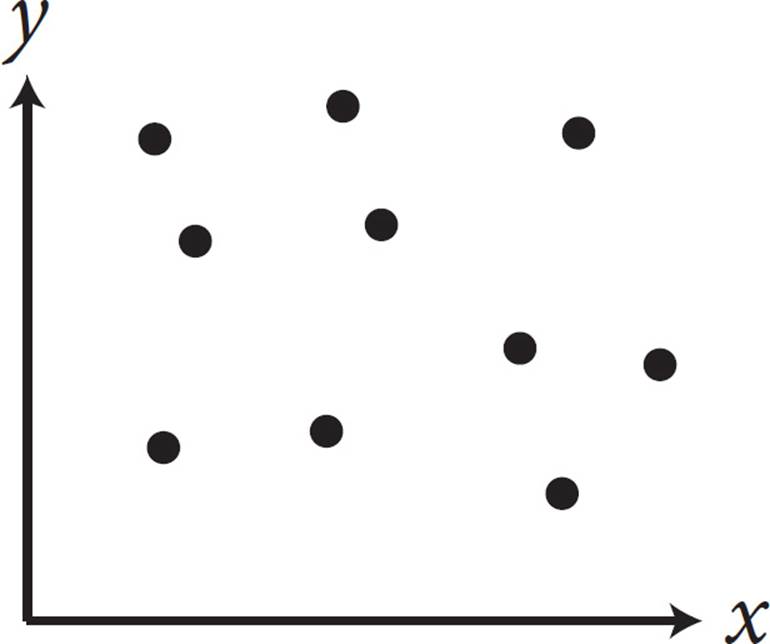

B)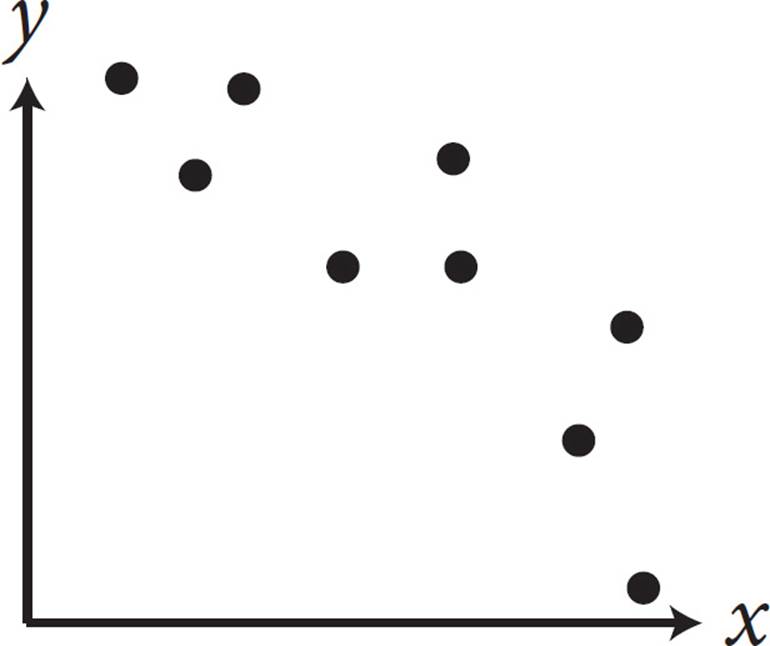

C)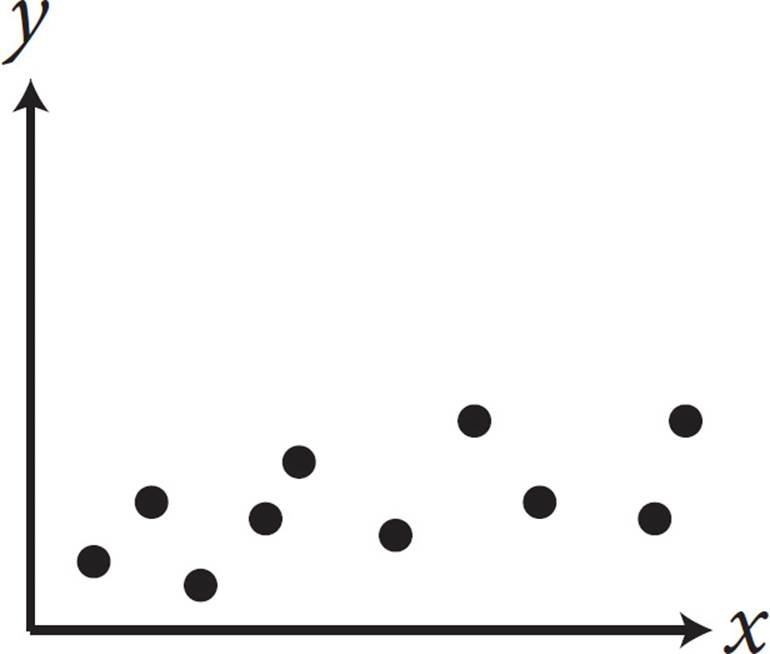

D)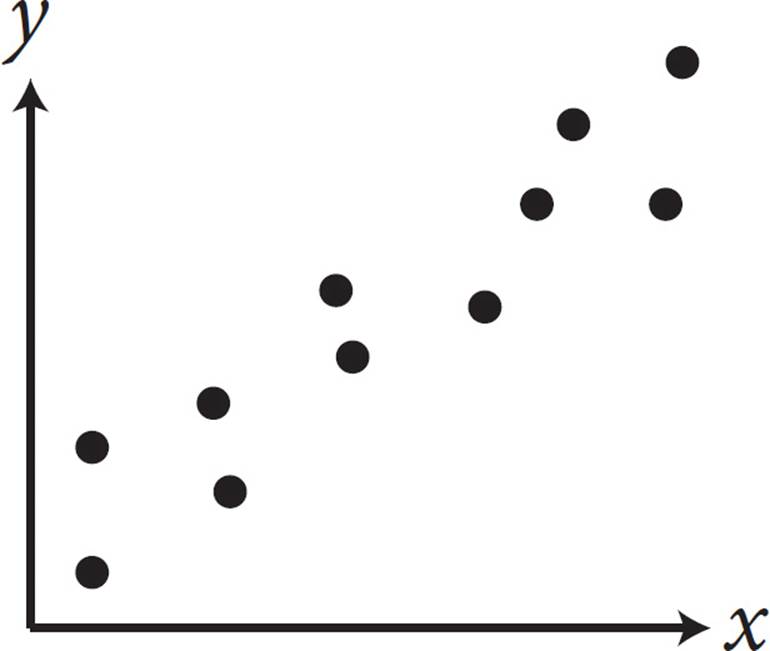

9.If 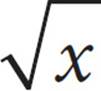+ 22 = 38, what is the value of x ?

A)4

B)16

C)32

D)256

14.If each number in the following sum were increased by t, the new sum would be 4.22. What is the value of t ?

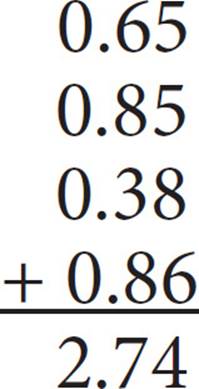
A)0.24

B)0.29

C)0.33

D)0.37

20.If 4^x · n² = 4^{x + 1} · n and x and n are both positive integers, what is the value of n ?

A)2

B)4

C)6

D)8

CHAPTER DRILL ANSWERS AND EXPLANATIONS

Drill 1

1.109

2.38

3.−3

4.10

5.15

Drill 2

1.6(57 + 13) = 6 × 70 = 420

2.51(48 + 50 + 52) = 51(150) = 7,650

3.ab + ac − ad

4.x(y − z)

5.c(ab + xy)

Drill 3

1.

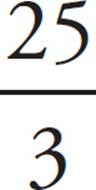
2.

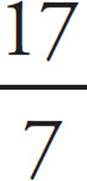
3.

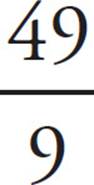
4.

5.

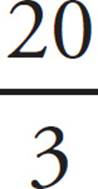
Drill 4

1.3

2.

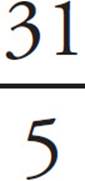
3.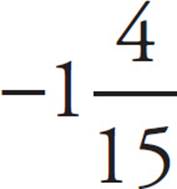 or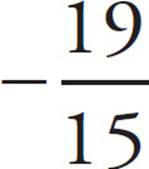

4.

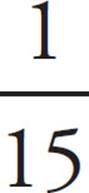
5.

6.

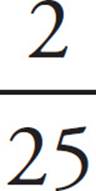
7.

Drill 5

Fundamentals Drill 1: No Calculator Section

1. ATake it one phrase at a time. The “sum” means you will add two things. The “squares of x and y” means to square x and square y, or x² and y². Add these to get x² + y². Cross out any choice that does not have x² + y² as the first part of the equation. Only (A) is left.

4. DPlug in the number given for a in the expression to find the value: −2 + (−2)² − (−2)³ + (−2)⁴ − (−2)⁵. Remember PEMDAS, the order of operations: The first thing to do here is deal with the Exponents, then we can take care of the Addition and Subtraction: −2 + 4 − (−8) + 16 − (−32), which simplifies to −2 + 4 + 8 + 16 + 32 = 58, (D).

6. CNegative exponents mean to take the reciprocal and apply the positive exponent. So 9⁻² = 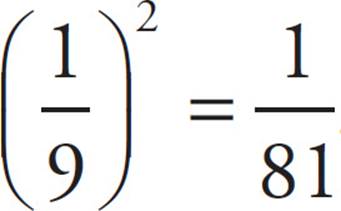. Now find what power of equals 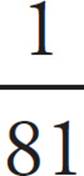. Because 3⁴ = 81, 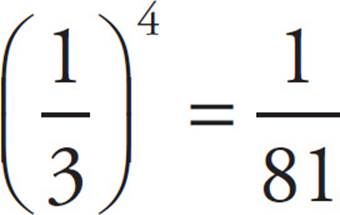, and x must be 4. The correct answer is (C).

7. BThe lowest number that both 8 and 10 are factors of is 40. Convert the fractions to a denominator of 40: 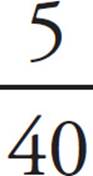+ 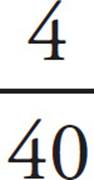= 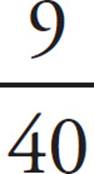. There is no factor that 9 and 40 have in common, so the fraction cannot be reduced. The number in place of a in is 9, so the answer is (B). Be careful! The value of b is in (D).

Fundamentals Drill 2: Calculator-Permitted Section

1. CTranslate the words into math: 7 × n = 84, and we want to know the value of 4n. 7n = 84, so n = 12, and 4n = 48, (C).

4. DFirst, solve for x. Divide both sides of the equation by 3, and you get x = 4. Then divide 24 by 4, which gives you 6, which is (D).

6. DA “strong positive association” means that as one variable increases, the other one increases. This will be shown as a line that angles through the graph from the lower left to the upper right. These scatterplots don’t have any lines of best fit drawn on them, so imagine the line that would go through most of the points on each graph. In (A), the points are all over the place, so no line of best fit can even be drawn. Eliminate (A). In (B), the line that hits most of the points would go from the upper left to the lower right. This is a negative association, not a positive one, so eliminate (B). In (C), the line would go straight across, parallel to the x-axis. This is not a positive association, so eliminate (C). The correct answer is (D).

9. DTo solve this equation, get 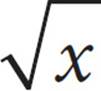by itself. 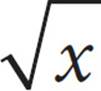= 16, so square both sides: (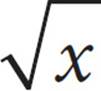)² = 16², so x = 256. Choice (D) is correct.

14. DTo figure out how much you need to add to 2.74 to get to 4.22, take 4.22 − 2.74 on your calculator. The difference between the two numbers is 1.48. This increase reflects the same number, t, added to each of the four numbers on the list. Divide 1.48 by 4 to find that t = 0.37, which is (D).

20. BFirst simplify the equation 4x • n² = 4^x+1 • n to 4x • n = 4^x+1, and then try an easy number for x. If x = 2, then 4² • n = 4²⁺¹. Since 16n = 4³, then 16n = 64 and n = 4. The correct answer is (B).

Summary

○There are only six arithmetic operations tested on the SAT: addition, subtraction, multiplication, division, exponents, and square roots.

○These operations must be performed in the proper order (PEMDAS), beginning with operations inside parentheses.

○Apply the distributive law whenever possible. Very often, this is enough to find ETS’s answer.

○A fraction is just another way of expressing division.

○You must know how to add, subtract, multiply, and divide fractions. Don’t forget that you can also use your calculator in the section where it is permitted.

○If any problems involving large or confusing fractions appear, try to reduce the fractions first. Before you multiply two fractions, for example, see if it’s possible to reduce either or both of the fractions.

○If you know how to work out fractions on your calculator, use it when it is allowed to help you with questions that involve fractions. If you intend to use your calculator for fractions, make sure you practice. You should also know how to work with fractions the old-fashioned way.

○A decimal is just another way of expressing a fraction.

○When a calculator is permitted, use it to add, subtract, multiply, and divide decimals. When the calculator is not allowed, try rounding and estimating before doing the math with your pencil and paper.

○Exponents are a kind of shorthand for expressing numbers that are the product of the same factor multiplied over and over again.

○To multiply two exponential expressions with the same base, add the exponents.

○To divide two exponential expressions with the same base, subtract the exponents.

○To raise one exponential expression to another power, multiply the exponents.

○To remember the exponent rules, think MADSPM.

○When you raise a positive number greater than 1 to a power greater than 1, the result is larger. When you raise a positive fraction less than 1 to an exponent greater than 1, the result is smaller. A negative number raised to an even power becomes positive. A negative number raised to an odd power remains negative.

○When you’re asked for the square root of any number, 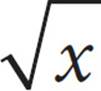, you’re being asked for the positive root only.

○Here are the only rules regarding square roots that you need to know for the SAT:

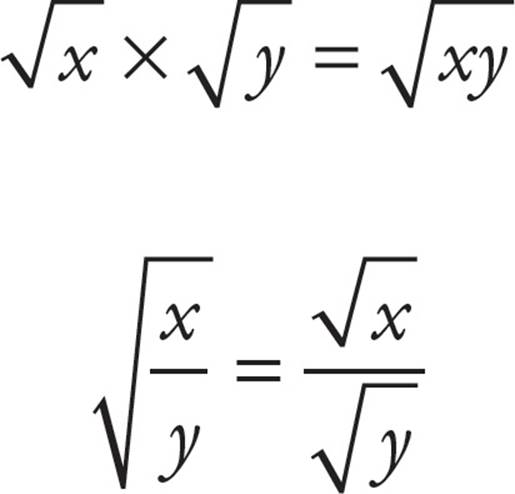
○The rule for fractional exponents is this:

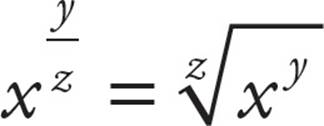
○The rule for negative exponents is this:

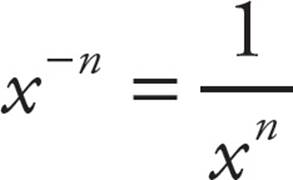
○When you encounter charts, carefully check the chart for information you should note, and remember that you can use your answer sheet as a ruler to help you locate information or to draw a line of best fit.