Cracking the New SAT with 4 Practice Tests, 2016 Edition (2015)

Part IV. How to Crack the Math Test

Chapter 13. Other Algebra Strategies

Now that you’re familiar with the basics of algebra, it’s time to learn how to avoid using algebra on the SAT. Yes, you read that correctly. Algebra problems on the SAT are filled with traps carefully laid by the test writers, so you need to know how to work around them. This chapter gives you the strategies you need to turn tricky algebra problems into simple arithmetic.

PRINCETON REVIEW ALGEBRA, OR HOW TO AVOID ALGEBRA ON THE SAT

Now that you’ve reviewed some basic algebra, it’s time for some Princeton Review algebra. At The Princeton Review, we like to avoid algebra whenever possible, and we’re going to show you how to avoid doing algebra on the SAT. Now, before you start crying and complaining that you love algebra and couldn’t possibly give it up, just take a second to hear us out. We have nothing against algebra—it’s very helpful when solving problems, and it impresses your friends—but on the SAT, using algebra can actually hurt your score. And we don’t want that.

We know it’s difficult to come to terms with this. But if you use algebra on the SAT, you’re doing exactly what the test writers want you to do. You see, when the test writers design the problems on the SAT, they expect the students to use algebra to solve them. Many SAT problems have built-in traps meant to take advantage of common mistakes that students make when using algebra. But if you don’t use algebra, there’s no way you can fall into those traps.

Plus, when you avoid algebra, you add one other powerful tool to your tool belt: If you are on Section 4, you can use your calculator! Even if you have a super-fancy calculator that plays games and doubles as a global positioning system, chances are it doesn’t do algebra. Arithmetic, on the other hand, is easy for your calculator. It’s why calculators were invented. Our goal, then, is to turn all the algebra on the SAT into arithmetic. We do that using something we call Plugging In.

My Best Friend

Plugging In allows you
to use your calculator
on many of the algebra
problems that show up in
Section 4!

PLUGGING IN THE ANSWERS (PITA)

Algebra uses letters to stand for numbers. You don’t go to the grocery store to buy x eggs or y gallons of milk. Most people think about math in terms of numbers, not letters that stand for numbers.

You should think in terms of numbers on the SAT as much as possible. On many SAT algebra problems, even very difficult ones, you will be able to find ETS’s answer without using any algebra at all. You will do this by working backward from the answer choices instead of trying to solve the problem using your standard math-class methods.

Plugging In The Answers is a technique for solving word problems in which the answer choices are all numbers. Using this powerful technique can solve many algebra problems on the SAT simply and quickly.

In algebra class at school, you solve word problems by using equations. Then, you check your solution by plugging in your answer to see if it works. Why not skip the equations entirely by simply checking the four possible solutions ETS offers on the multiple-choice questions? One of these must be the correct answer. You don’t have to do any algebra, you will seldom have to try more than two choices, and you will never have to try all four. Note that you can use this technique only for questions that ask for a specific amount.

Here’s an example:

9.Zoë won the raffle at a fair. She will receive the prize money in 5 monthly payments. If each payment is half as much as the previous month’s payment and the total of the payments is $496, what is the amount of the first payment?

A)$256

B)$96

C)$84

D)$16

Here’s How to Crack It

ETS would like you to go through all of the effort of setting up this equation:

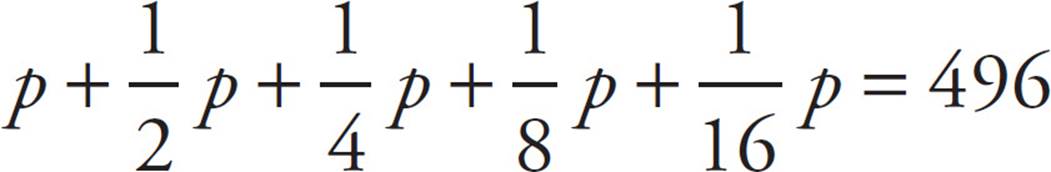
Then, of course, they want you to solve the equation. But, look at all those fractions! There are plenty of opportunities to make a mistake and you can bet that ETS has figured most of them out so they can have a trap answer waiting. So, let’s work with the answers instead.

To work with the answer choices, first you need to know what they represent so that you can label them. In this case, the question asks for the first payment, so write something like “first payment” over the answers.

Representation

Make sure you know what
the numbers in the answer
choices represent. Be sure
to label them!

Now, it’s time to start working the steps of the problem. But first, notice that the answer choices are in numerically descending order. ETS likes to keep their problems organized so they will always put the answers in order. You can use that to your advantage by starting with one of the middle answer choices. Let’s try (C).

Grab (C) and ask yourself, “If the first payment is $84, what’s the next thing I can figure out?” In this case, you could figure out the second payment.

So, make a chart and write down 42 (half of 84) next to the 84. Keep doing that to find the values of the third, fourth, and fifth payments. When you have worked all the steps, your problem should look like this:

9.Zoë won the raffle at a fair. She will receive the prize money in 5 monthly payments. If each payment is half as much as the previous month’s payment and the total of the payments is $496, what is the amount of the first payment?

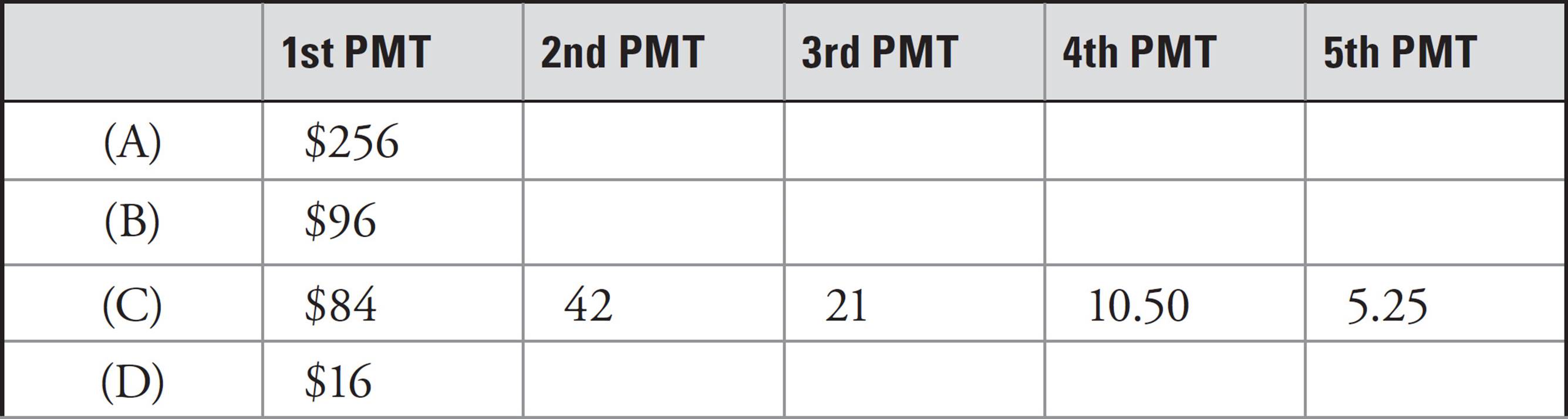
You need to determine if that was the correct answer. The problem says that the total is supposed to be $496, so add up the payments: 84 + 42 + 21 + 10.50 + 5.25 = 162.75, which is much smaller than 496. So, cross off (C) and (D).

Now, all you need to do is try (B). If (B) works, then you’re done. And, if (B) doesn’t work, you’re still done because the answer must be (A). That’s putting your POE to good use! If the first payment is $96, then the payments are 96 + 48 + 24 + 12 + 6 = 186, which is still too small. That means the answer must be (A), and you don’t really need to check it.

Here are the steps for solving a problem using the PITA approach:

To solve a problem by Plugging In The Answers:

1.Label the answer choices.

2.Starting with one of the middle answer choices, work the steps of the problem. Be sure to write down a label for each new step.

3.Look for something in the problem that tells you what must happen for the answer to be correct.

4.When you find the correct answer, STOP.

6.

2x + y = 6

7x + 2y = 27

The system of equations above is satisfied by which of the following ordered pairs (x, y) ?

A)(−5, 4)

B)(4, −2)

C)(5, 4)

D)(5, −4)

Which Way?

Sometimes, it’s hard to
tell if you need a larger
number or a smaller number
if the first answer you
tried didn’t work. Don’t
fret. Just pick a direction
and go! Spend your time
trying answers rather than
worrying about going in
the wrong direction.

Here’s How to Crack It

When you feel the urge to do a whole lot of algebra, it is a good time to check whether it would be possible to just plug in the answers instead. In this case, trying your answer choices will be not only effective but also incredibly fast.

It doesn’t seem like we will be able to tell whether to move up or down this time, as the ordered pairs don’t really have an ascending or descending order, but let’s start in the middle anyway. Even if you end up trying all four, you will be saving time by plugging in the answers instead of solving.

Starting with (B) gives you 4 for x and −2 for y. Try that out in the first equation: 2(4) + (−2) = 6. That matches the first equation, so this is a possibility. Let’s try it out in the second equation: 7(4) + 2(−2) = 24. That does not match the second equation, so you can eliminate (B).

Let’s try out (C) next. If x = 5 and y = 4, then 2(5) + 4 = 14, and you wanted it to be 6, so you can eliminate this answer choice, too.

Let’s move on to (D). That would give you 2(5) + (−4) = 6. So far so good! Let’s try the second equation to see if this choice satisfies both: 7(5) + 2(−4) = 27. Since (D) satisfies both equations, this is your answer!

You may recall that we covered questions like this in the last chapter. It is important to know how to solve these, in case a question like this comes up in the Grid-In part of a Math section. When you have answers available to you, though, don’t be afraid to use them!

One last thing about PITA: Here’s how you spot that you should use this approach to solve the problem.

Three ways to know that it’s time for PITA:

1.There are numbers in the answer choices.

2.The question asks for a specific amount such as “what was the first payment.”

3.You have the urge to write an algebraic equation to solve the problem.

Plugging In the Answers: Advanced Principles

Plugging In the Answers works the same way on difficult problems as it does on easy and medium ones. You just have to watch your step and make certain you don’t make any careless mistakes.

Here’s one example:

12.A bakery sold exactly 85% of the cupcakes it baked on Tuesday. Which of the following could be the total number of cupcakes baked on Tuesday?

A)150

B)145

C)140

D)130

Here’s How to Crack It

Is your first reaction that there isn’t nearly enough information here to start on this problem? That makes it a great opportunity to plug in the answers! Let’s start with one of the middle answer choices and test it out. Sometimes, even if you can’t see how a problem works ahead of time, it starts to make a lot more sense once you put real numbers into it.

Choice (B) is 145, but 145 what? Read the question very carefully. The question asks for the total number of cupcakes baked on Tuesday, so label the column of answer choices “Total.”

Next, work your way through the problem. If 145 is the total number of cupcakes baked on Tuesday, the number the bakery sold on Tuesday is 85% of 145, or 123.25. Have you ever bought 0.25 cupcakes at a bakery? It would be really weird for a bakery to sell fractions of cupcakes, so this answer could not be the total number baked on Tuesday.

In this particular question, it is hard to tell whether you should try bigger or smaller numbers next, but you have learned two things from your first attempt: You can get rid of (B), and the correct answer will be the one that gives you a whole number of cupcakes. Instead of spending time trying to predict which direction to go for the answer, let’s just get to work on the other answer choices.

We’ll try (C) next. If the bakery baked 140 cupcakes on Tuesday, they sold 85% of 140, or 119. Is there anything wrong with selling 119 cupcakes? No! Since the bakery sold only whole cupcakes, you can select (C).

Here’s another example:

7.For what value of x is |2x + 3| + 5 = 0 ?

A)−4

B)0

C)4

D)There is no such value of x.

Here’s How to Crack It

Although we covered it in the last chapter, solving algebraically on an absolute value question can be treacherous: There are so many ways to go wrong with those signs! Luckily, this absolute value question comes complete with answer choices, so we can simply plug in the answers to get a solution.

Hey, Smarty!

If you think you can
improve your SAT Math
score without learning
to plug in, you’re in for
an unpleasant surprise.
Seriously, this technique
works. Just bear in mind
that this is a multiple-
choice test; the correct
answers are already right
there on the page.

Let’s start with (C). When you put 4 in for x, you get |2(4) + 3| + 5 = 0, or 16 = 0. This is clearly not true, so cross off (C) and move on to (B). If x is 0, then the original equation says |2(0) + 3 | + 5 = 0 or 8 = 0, so you can eliminate (B), too. Let’s try (A). |2(−4) + 3 | + 5 = 0 could be rewritten as |−8 + 3 | + 5 = 0, or |−5| + 5 = 0. As long as you remember that the absolute value of a number is always positive, it is clear that this gives you 5 + 5 = 0. Since this is also clearly untrue, eliminate (A), and choose (D). Apparently, there is no such value of x!

Solving Rational Equations

A rational equation is basically an equation in which one (or more) of the terms is a fractional one. Rational equations look scary, but there are very simple ways of solving them. One way is to factor out like terms and then cancel. All in all, ETS can’t get too messy here, so they will keep the math nice and tidy.

Try one:

18.If 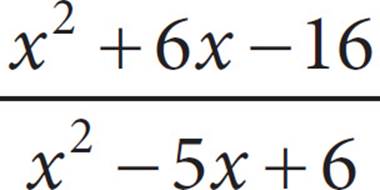= 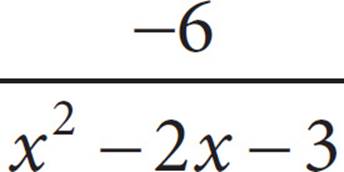, then which of the following could be a value of x ?

A)−7

B)−5

C)0

D)6

Quick and Painless

Use PITA! Just be careful
with your calculations,
since you can’t use your
calculator.

Here’s How to Crack It

Hate factoring? PITA! Start with (C) and plug in 0 for x. Does everything work out? In this case, it doesn’t. Keep trying other answer choices until you find one that works. Choice (A) does, so that’s the correct answer choice. See? These are all bark and no bite.

Solving Radical Equations

We covered this topic in the previous chapter, but here’s another example of solving radical equations using the PITA approach.

11.

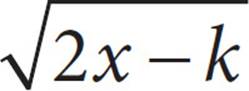= 3 − x

If k = 3, what is the solution set of the equation above?

A){−2}

B){2}

C){2, 6}

D){6}

Here’s How to Crack It

In the last chapter, we showed you how to solve these—a necessary skill if there are no answer choices to plug in. Here, PITA is definitely the way to go. Start by plugging in the value given for k, which is 3. The equation becomes 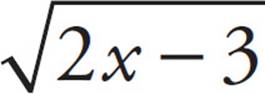= 3 − x.

Now pick a value for x from the answer choices and plug it into the equation to see if it works. Rather than starting with a specific answer choice, start with a number that appears more than once in the answers, such as x = 2. The equation becomes 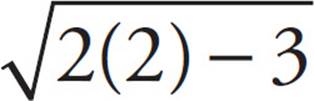= 3 − 2, then 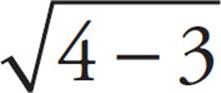= 1, and 1 = 1. That’s true, so eliminate (A) and (D), which don’t include 2.

Try it again with x = 6 to see if the correct answer is (B) or (C). You get 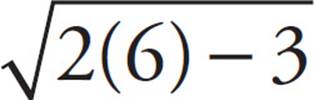= 3 − 6 or 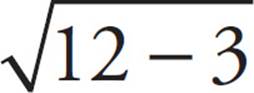= −3. This doesn’t work, so eliminate (C) and choose (B).

PLUGGING IN YOUR OWN NUMBERS

Plugging In the Answers enables you to find the answer to problems whose answer choices are all numbers. What about problems that have answer choices containing variables? On these problems, you will usually be able to find the answer by Plugging In your own numbers.

Plugging In is easy. It has three steps:

1.Pick numbers for the variables in the problem.

2.Use your numbers to find an answer to the problem. Circle your answer.

3.Plug your numbers from step 1 into the answer choices to see which choice equals the answer you found in step 2.

The Basics of Plugging In Your Own Numbers

This sort of Plugging In is simple to understand. Here’s an example:

13.Which of the following is equivalent to the expression ?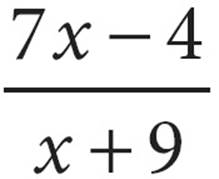

A)7 −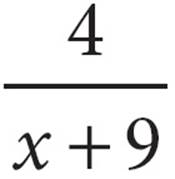

B)7 −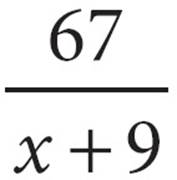

C)7 −

D)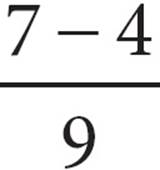

Here’s How to Crack It

First, pick a number for x. Pick something easy to work with, like 2. In your test booklet, write x = 2, so you won’t forget. If x = 2, then 7x − 4 = 10, and x + 9 = 11. So, when x = 2, the expression in the problem equals 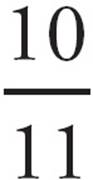. Circle it! That is your target answer. When you find the answer choice that also gives you 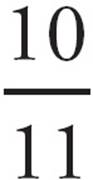when you plug in x = 2, you will know you have found an equivalent expression.

Start with the easier answer choices: (C) and (D). For (C), does 7 − = 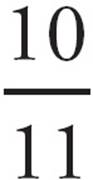? No! Eliminate it and move on to (D): 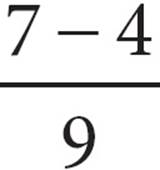also does not equal your target answer, so it cannot be an equivalent expression.

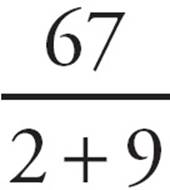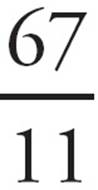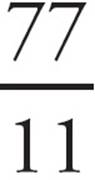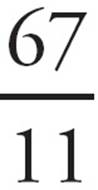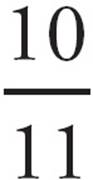Let’s try (B): When you put in 2 for x, you get 7 − = 7 − = − = . This is the number that you are looking for. Unlike PITA, when you plug in your own numbers, you must check all four answer choices, just in case more than one works. Go ahead and try the last answer just to make sure that you’re right. Choice (A) does not give you your target answer, so you know that (B) is the one!

Get Real

Trying to imagine how
numbers behave in the
abstract is a waste of
time. So, if the problem
says that Tina is x years
old, why not plug in your
own age? That’s real
enough. You don’t have to
change your name to Tina.

Here’s another example:

19.During a special sale at a furniture store, Erica bought a floor lamp at a 10% discount. She paid a total of t dollars, which included the discounted price of the floor lamp and a 6% sales tax on the discounted price. In terms of t, what was the original price of the floor lamp?

A)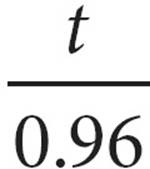

B)(0.9)(1.06) t

C)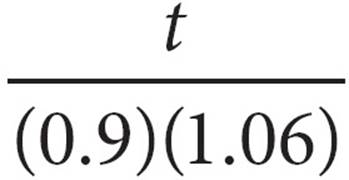

D)0.96t

Here’s How to Crack It

This could be a pretty tricky algebra question, but if you read the question carefully and plug in easy numbers, it will be a breeze.

Let’s start at the beginning. When Erica bought that floor lamp on sale, what did you really wish you knew? It would be very helpful to start this problem knowing the original price of the floor lamp. So, let’s start plugging in there. Plug in something you know how to take a percentage of, say 100. Write down “original = 100” on your scratch paper and move on the next step of the problem. Erica got a 10% discount, so take 10% of the original price. That means she got a $10 discount, and the discounted price of her floor lamp was $90. Write that down and move on to the sales tax. If you read carefully, it is clear that the sales tax is 6% of the discounted price. So, you need to take 6% of the $90 discounted price, or $5.40. To get her total, add the $5.40 of tax to the $90 for the discounted floor lamp, and you get $95.40. This is where the careful reading comes in. The variable t in this problem is supposed to be the total amount she paid, so make sure that you label this on your scratch paper “t = $95.40”.

Next, read the last sentence of the question again, to be sure you know which of the answers is your target answer. The question asks for the original price of the floor lamp, so circle the number you plugged in for the original price. Your target answer is 100.

On to the answer choices! When you put $95.40 in for t in (A), you get 99.375. This is not your target answer, so you can eliminate (A). Choice (B) gives you 91.0116, so that will not work, either. Plugging in $95.40 into (C) yields the target of 100, so hang on to it while you check (D) just in case. When you plug in for (D), you get 91.584. Since that does not match your target, you can eliminate (D), and select (C)!

Which Numbers?

Although you can plug in any number, you can make your life much easier by plugging in “good” numbers—numbers that are simple to work with or that make the problem easier to manipulate. Picking a small number, such as 2, will usually make finding the answer easier. If the problem asks for a percentage, plug in 100. If the problem has to do with minutes, try 30 or 120.

Except in special cases, you should avoid plugging in 0 and 1; these numbers have weird properties. Using them may allow you to eliminate only one or two choices at a time. You should also avoid plugging in any number that appears in the question or in any of the answer choices. Using those numbers could make more than one answer match your target. If more than one answer choice matches your target, plug in a new number and check those answer choices. You may have to plug in more than once to eliminate all three incorrect answers.

Be Good

“Good” numbers make a
problem less confusing by
simplifying the arithmetic.
This is your chance to
make the SAT easier.

Many times you’ll find that there is an advantage to picking a particular number, even a very large one, because it makes solving the problem easier.

Here’s an example.

14.If 60 equally priced downloads cost x dollars, then how much do 9 downloads cost?

A)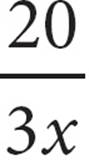

B)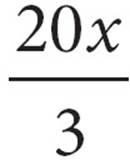

C)60x + 9

D)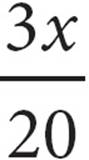

Here’s How to Crack It

Should you plug in 2 for x? You could, but plugging in 120 would make the problem easier. After all, if 60 downloads cost a total of $120, then each download costs $2. Write x = 120 in your test booklet.

If each download costs $2, then 9 downloads cost $18. Write an 18 in your test booklet and circle it. You are looking for the answer choice that works out to 18 when you plug in $120 for x. Let’s try each choice:

A)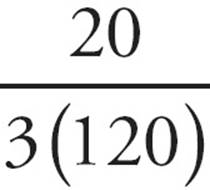 ≠ 18

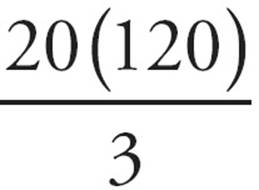B) ≠ 18

C)60(120) + 9 ≠ 18;

D)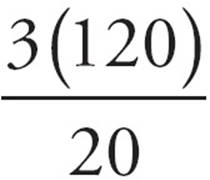 = 18 Here’ your answer.

Let’s try another example.

20.A watch loses x minutes every y hours. At this rate, how many hours will the watch lose in one week?

A)7xy

B)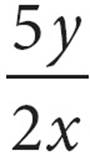

C)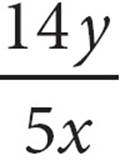

D)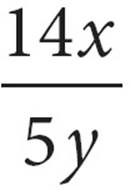

Here’s How to Crack It

This is an extremely difficult problem for students who try to solve it using math-class algebra. You’ll be able to find the answer easily, though, if you plug in carefully.

What numbers should you plug in? As always, you can plug in anything. However, if you think just a little bit before choosing the numbers, you can make the problem easier to understand. There are three units of time—minutes, hours, and weeks—and that’s a big part of the reason this problem is hard to understand. If you choose units of time that are easy to think about, you’ll make the problem easier to handle.

Start by choosing a value for x, which represents the number of minutes that the watch loses. You might be tempted to choose x = 60 and that would make the math pretty easy. However, it’s usually not a good idea to choose a conversion factor such as 60, the conversion factor between minutes and hours, when plugging in. When dealing with time, 30 is usually a safer choice. So, write down x = 30.

Next, you need a number for y, which represents the number of hours. Again, you might be tempted to use y = 24 but that’s the conversion factor between hours and days. So, y = 12 is a safer choice. Write down y = 12.

Now, it’s time to solve the problem to come up with a target. If the watch loses 30 minutes every 12 hours, then it loses 60 minutes every 24 hours. Put another way, the watch loses an hour each day. In one week, the watch will lose 7 hours. That’s your target so be sure to circle it.

Now, you just need to check the answer choices to see which one gives you 7 when x = 30 and y = 12.

A)7xy = 7(30)(12) = Something too big! Cross it off.

B)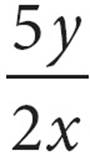 = = 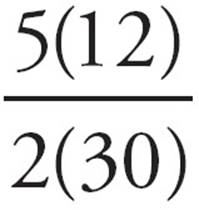= 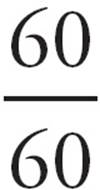1. Also wrong.

C)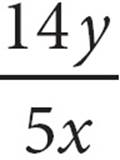 = = 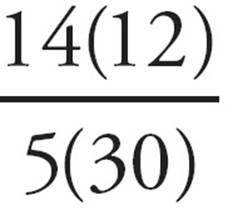= 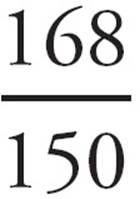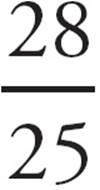Cross it off.

D)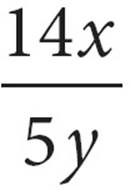 = = 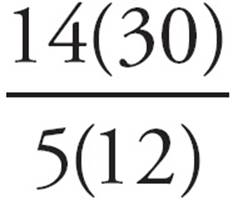= 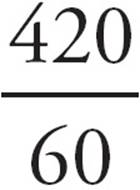7. Choose it!

Inequalities

Plugging In works on problems containing inequalities, but you will have to follow some different rules. Plugging in one number is often not enough; let’s look at an example where this is the case.

6.Mammoth Printing Company charges a fee of $28 to print an oversized poster, and $7 for each color of ink used in the poster. Colossal Printing charges a fee of $34 to print an oversized poster and $5.50 for each color of ink used. If x represents the number of colors of ink used to print a poster, what are all the values of x for which Mammoth Printing Company would charge more to print the poster than Colossal Printing?

A)x < 4

B)2 ≤ x ≤ 4

C)4 ≤ x ≤ 7

D)x > 4

Here’s How to Crack It

Since you are looking for an amount that would make the Mammoth Printing Company’s price greater than Colossal Printing’s price, you have an inequality.

Plugging In on an inequality question means selecting a value for x that answers the question, and then comparing it to the inequalities in the answer choices. Remember, you may have to try more than one number with inequality questions, since the number you try first may satisfy the inequality in more than one answer choice!

Let’s start out by trying something small, like x = 2. Since x is the number of colors of ink used, Mammoth Printing Company would charge $28 to print the poster, plus $7 for each of the 2 colors, for a total of $42. Colossal Printing would charge $34 to print the poster, plus $5.50 for each of the 2 colors, or $45 total. That means that when x = 2, Mammoth Printing Company would charge less than Colossal Printing, and 2 is not a number that works as a solution to this problem.

Let’s try something bigger, say x = 5. If the poster had 5 colors, Mammoth Printing Company would charge $28 to print the poster, plus $7 for each of the 5 colors, for a total of $63. Colossal Printing would charge $34 to print the poster, plus $5.50 for each of the 5 colors, or $61.50 total. That means that when x = 5, the price Mammoth charges would be more than Colossal’s price, so this is a possible value for x.

Once you have a value for x that satisfies the question, it’s time to move to the answer choices. You should eliminate (A) and (B), because x = 5 does not satisfy either of those inequalities. Choices (C) and (D) are satisfied when x = 5, so they are still possible.

Next, you need to find a number that will satisfy the inequality in one of the remaining answer choices but not the other, so you can determine whether (C) or (D) is your final answer. Looking at our answer choices, we can see that we will have to think about plugging in something that will eliminate one answer choice but not the other. Let’s try out x = 4, because it satisfies (C) but not (D). Mammoth Printing Company would charge $56 for a 4 color poster.

$28 + $7(4) = $56

Colossal Printing would also charge $56 for a 4 color poster.

$34 + $5.50(4) = $56

Since Mammoth would not charge more to print the poster than Colossal, you can eliminate (C) and choose (D).

Using different integers got you down to one answer choice on that question. Sometimes, to find ETS’s answer, you may have to plug in several numbers, including weird numbers like −1, 0, 1, , and − .

Weird Numbers

As you may have noticed,
some numbers have
uncommon properties.
Because of this, we plug
them in only under certain
circumstances, usually
when solving
• inequalities
• MUST BE problems

The five numbers just mentioned all have special properties. Negatives, fractions, 0, and 1 all behave in peculiar ways when, for example, they are squared. Don’t forget about them!

Plugging In: Advanced Principles

If there are variables in the answer choices, you should definitely consider Plugging In. However, sometimes a question will be a Plug In question that doesn’t have variables in the answer choices. It is, instead, a hidden Plug In question. It will refer to some unknown amount, but never actually give you a number. So, you’re going to have to make up your own number.

Here’s an example.

15.

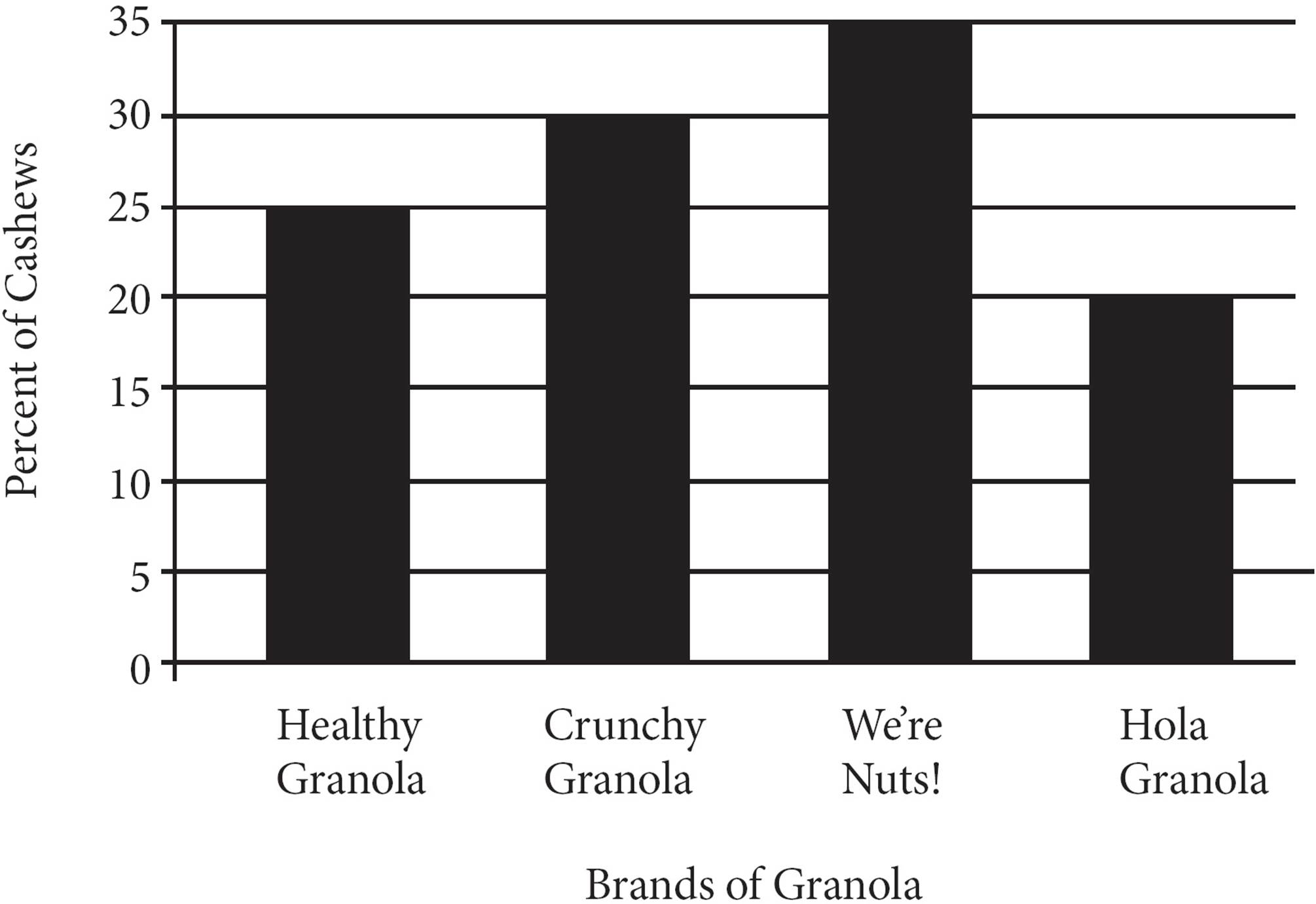
Vik is deciding which brand of granola to buy. He prefers granola with a lot of cashews, so he has made a chart (above) showing the cashew content, as a percentage of the total weight of the granola, of each of the 4 leading brands of bulk granola. If Healthy Granola costs $4 a pound, Crunchy Granola costs $5.40 a pound, We’re Nuts! Granola costs $7.00 a pound, and Hola Granola costs $5 a pound, which brand of granola would offer Vik the greatest amount of cashews per dollar?

A)Healthy Granola

B)Crunchy Granola

C)We’re Nuts!

D)Hola Granola

Here’s How to Crack It

This is one of those questions that has so much information in it, it is almost impossible to know where to start. It doesn’t help that all the amounts are percentages, and you don’t even know the total amount of granola Vik is going to buy. That feeling that you wish you had some real amount to start with tells you that this is a great opportunity to plug in, even though there are no variables in the answer choices. This is a Hidden Plug In.

You have already realized that the most helpful thing to know here would be how much granola Vik will buy, so start by plugging in for that amount. The easiest number to plug in when you will be using percentages is 100, so even though it is a pretty ridiculous amount of granola for one guy, let’s find out what happens if Vik buys 100 pounds of granola. Write down “total = 100 pounds” in your test booklet, and start to work the problem one piece at a time.

Once you have a 100 pound total, it is relatively simple to come up with the amount of cashews in each granola. Keep track of them in your test booklet:

100 lbs Healthy Granola = 25 lbs of cashews

100 lbs Crunchy Granola = 30 lbs of cashews

100 lbs We’re Nuts! = 35 lbs of cashews

100 lbs Hola Granola = 20 lbs of cashews

The next piece is price. Add the price of 100 pounds of each granola to your scratch paper:

100 lbs Healthy Granola = 25 lbs of cashews = $400 total

100 lbs Crunchy Granola = 30 lbs of cashews = $540 total

100 lbs We’re Nuts! = 35 lbs of cashews = $700 total

100 lbs Hola Granola = 20 lbs of cashews = $500 total

With this information, you can start to figure out how much Vik is paying per pound of cashews.

Healthy Granola contains 25 lbs of cashews for $400. If you do the math, that is $400 ÷ 25 lbs cashews or $16 per pound of cashews. Crunchy Granola costs $540 for 30 lbs of cashews or $540 ÷ 30 lbs cashews = $18/lb cashews. Since this is more expensive, you can eliminate (B). This is not how Vik is going to get the greatest amount of cashews per dollar. We’re Nuts!, besides having a great name, also has a really high percentage of cashews. You might think that would be Vik’s best buy, but when you do the math, $700 for 35 lbs of cashews is $700 ÷ 35 lbs cashews or $20/lb cashews. This is less cashew per dollar than (A), so eliminate (C). Hola Granola costs $500 for 20 lbs of cashews, and $500 ÷ 20 lbs cashews is going to come out to a whopping $25/lb cashews. That is definitely not the best deal on cashews, so eliminate (D).

Apparently, nothing is going to beat Healthy Granola in terms of the cashew content per dollar! You can choose (A), and leave Vik to figure out what he is going to do with all that granola.

Meaning in Context

Some questions, instead of asking you to come up with an equation, just want you to recognize what a part of the equation stands for. It sounds like a simple enough task, but when you look at the equation, they have made it really hard to see what is going on. For this reason, Meaning in Context questions are a great opportunity to plug in real numbers and start to see how the equation really works!

First things first, though, you want to think about your POOD: Does this question fit into your pacing goals? It might take a bit of legwork to get an answer, and you may need that time to go collect points on easier, quicker questions.

If this question does fit into your pacing plan, you should read carefully, label everything you can in the equation, and POE to get rid of any answer choices that are clearly on the wrong track. Then, it’s time to plug some of your own numbers in to see what is going on in there.

Here’s an example:

7.

n = 1,273 − 4p

The equation above was used by the cafeteria in a large public high school to model the relationship between the number of slices of pizza, n, sold daily and the price of a slice of pizza, p, in dollars. What does the number 4 represent in this equation?

A)For every $4 the price of pizza decreases, the cafeteria sells 1 more slice of pizza.

B)For every dollar the price of pizza decreases, the cafeteria sells 4 more slices of pizza.

C)For every $4 the price of pizza increases, the cafeteria sells 1 more slice of pizza.

D)For every dollar the price of pizza increases, the cafeteria sells 4 more slices of pizza.

Here’s How to Crack It

First, read the question very carefully, and use your pencil to label the variables. You know that p is the price of pizza, and n is the number of slices, so you can add that information to the equation. If you can, eliminate answer choices that don’t make sense. But what if you can’t eliminate anything, or you can eliminate only an answer choice or two?

Even with everything labeled, this equation is difficult to decode, so it’s time to plug in! Try a few of your own numbers in the equation, and you will get a much better understanding of what is happening.

Let’s try it out with p = 2. When you put 2 in for p, n = 1,273 − 4(2) or 1,265.

So, when p = 2, n = 1,265. In other words, at $2 a slice, the cafeteria sells 1,265 slices.

When p = 3, n = 1,261, so at $3 a slice, the cafeteria sells 1,261 slices.

When p = 4, n = 1,257, so at $4 a slice, the cafeteria sells 1,257 slices.

So now, let’s use POE. First of all, is the cafeteria selling more pizza as the price goes up? No, as the price of pizza goes up, the cafeteria sells fewer slices of pizza. That means you can eliminate (C) and (D).

Choice (A) says that for every $4 the price goes down, the cafeteria sells 1 more slice of pizza. Does your plugging in back that up? No. The cafeteria sells 8 more slices of pizza when the price drops from $4 to $2, so (A) is no good.

Now, let’s take a look at (B). Does the cafeteria sell 4 more slices of pizza for every dollar the price drops? Yes! Choice (B) is the correct answer.

Here are the steps for using Plugging In to solve Meaning in Context questions:

Meaning In Context

1.Read the question carefully. Make sure you know which part of the equation you are being asked to identify.

2.Use your pencil to label the parts of the equation you can identify.

3.Eliminate any answer choices that clearly describe the wrong part of the equation, or go against what you have labelled.

4.Plug in! Use your own numbers to start seeing what is happening in the equation.

5.Use POE again, using the information you learned from plugging in real numbers, until you can get it down to one answer choice. Or, get it down to as few choices as you can, and guess.

Let’s look at a slightly different one now.

10.

7x + y = 133

Jeffrey has set a monthly budget for purchasing frozen blended mocha drinks from his local SpendBucks coffee shop. The equation above can be used to model the amount of his budget, y, in dollars that remains after buying coffee for x days in a month. What does it mean that (19, 0) is a solution to this equation?

A)Jeffrey starts the month with a budget of $19.

B)Jeffrey spends $19 on coffee every day.

C)It takes 19 days for Jeffrey to drink 133 cups of coffee.

D)It takes 19 days for Jeffrey to run out of money in his budget for purchasing coffee.

Here’s How to Crack It

Start by labeling the x and the y in the equation to keep track of what they stand for. Use your pencil to write “days” above the x and “budget” above the y. So 7 × days + budget = 133. Hmm, still not very clear, is it? One way to approach this is to plug in the point. If x = days = 19 when y = budget = 0, then Jeffrey will have no budget left after 19 days. This matches (D).

If you have trouble seeing this, you can use the answer choices to help you plug in. If (A) is true, the budget at the start of the month, when days = 0, is $19. Plug these values into the equation to see if it is true. Is 7 × 0 + 19 = 133? Not at all, so eliminate (A). If (B) is true, Jeffrey drinks a lot of coffee! Let’s try some numbers and see if it works. For x = 1, the equation becomes 7(1) + y = 133 or y = 126, and for x = 2, it is 7(2) + y = 133 or y = 119. The difference in y, the budget remaining, is 126 − 119 = 7, so that’s not $19 per day. Eliminate (B) so only (C) and (D) remain. These both have 19 for the number of days, and the point (19, 0) would indicate that 19 is the x value, or days. If you saw that right away—great! That would allow you to skip right to testing (C) and (D).

For (C), you can plug in 19 for days in the equation to get 7 × 19 + budget = 133, or budget = 0. Does that tell you how many cups of coffee Jeffrey drank? You have no information about the cost of a single cup of coffee, so the answer can’t be (C). It does tell you, however, that after 19 days, Jeffrey has no budget left, so (D) is not only the one remaining answer, but it is also the correct one!

Algebra Strategies Drill 1: No Calculator Section

Work these algebra questions, without your calculator, using Plugging In or Plugging In the Answers. Answers and explanations can be found on this page.

5.The length of a certain rectangle is twice the width. If the area of the rectangle is 128, what is the length of the rectangle?

A)4

B)8

C)16

D)21

10.If xy < 0, which of the following must be true?

I. x + y = 0

II. 2y − 2x < 0

III. x² + y² > 0

A)I only

B)III only

C)I and III

D)II and III

13.If 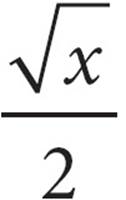= 2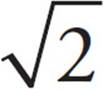, what is the value of x ?

A)4

B)16

C)16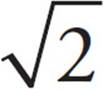

D)32

15.If y = 3^x and x and y are both integers, which of the following is equivalent to 9^x + 3^{x + 1} ?

A)y³

B)3y + 3

C)y(y + 3)

D)y² + 3

Algebra Strategies Drill 2: Calculator-Permitted Section

Feel free to use your calculator as needed to apply the Plugging In skills you’ve learned so far. Answers and explanations can be found on this page.

8.If Alex can fold 12 napkins in x minutes, how many napkins can he fold in y hours?

A)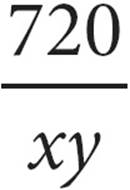

B)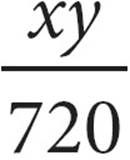

C)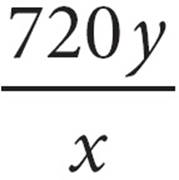

D)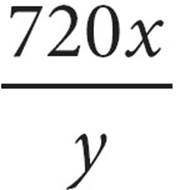

12.Nails are sold in 8-ounce and 20-ounce boxes. If 50 boxes of nails were sold and the total weight of the nails sold was less than 600 ounces, what is the greatest possible number of 20-ounce boxes that could have been sold?

A)33

B)25

C)17

D)16

18.If a is 63% of x and c is of x, which of the following is the closest equivalent of the ratio of a to c ?

A)0.236

B)0.381

C)0.595

D)1.680

21.If c = + and x > y > 0, then which of the following is equal to ?

A)x + y

B)x − y

C)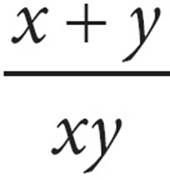

D)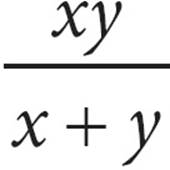

24.A gas station sells regular gasoline for $2.39 per gallon and premium gasoline for $2.79 per gallon. If the gas station sold a total of 550 gallons of both types of gasoline in one day for a total of $1,344.50, how many gallons of premium gasoline were sold?

A)25

B)75

C)175

D)475

25.There are k gallons of gasoline available to fill a tank. After d gallons have been pumped, in terms of k and d, what percent of the gasoline has been pumped?

A)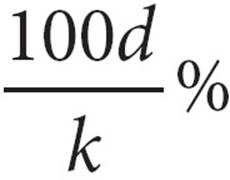

B)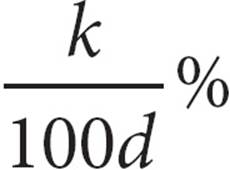

C)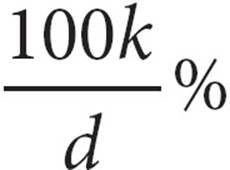

D)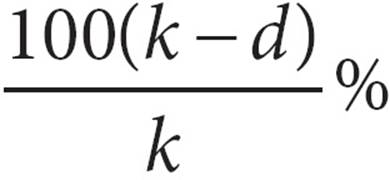

CHAPTER DRILL ANSWERS AND EXPLANATIONS

Algebra Strategies Drill 1: No Calculator Section

5. CPlug in the answers. If you start with (B), the length is 8, and the width is half that, or 4. Area is length × width. The area of this rectangle is 8 × 4, which is nowhere near 128. Eliminate (A) and (B), as both are too small. Try (C): If the length is 16, the width is 8. So, does 128 = 16 × 8? You could write it all out, since you can’t use your calculator, but you can also estimate. 16 × 10 = 160, so 16 × 8 would be about 130. The number in (D) is too large and will give a weird fraction, so (C) is correct. Alternatively, write an equation. The equation is area = w × 2w. So, 128 = 2w². Divide by 2 to get 64 = w². Take the square root of both sides to find w = 8. The length is twice this width, so length = 2 × 8 = 16, and the answer is (C).

10. BA question with unknown variables indicates a good place to plug in. You need numbers for x and y that will give you a negative product. Try x = 1 and y = −2. If you plug these into the statements in the Roman numerals, you find that (I) is false, but (II) and (III) are true. You can eliminate any answer choice that contains (I). This leaves (B) and (D). Now try different numbers to see if you can eliminate another choice. If you try x = −1 and y = 2, you find that (II) is false and (III) is still true. This leaves you with (B) as the only correct answer.

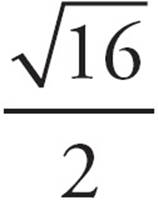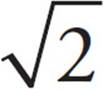13. DPlug in the answers, starting with (B). If x = 16, the left side of the equation is = = 2. Does that equal 2? No—it’s too small. Choice (C) is ugly to work with, so try (D) next. If it is too big, (C) is your answer. For (D), x = 32, and the left side of the equation becomes 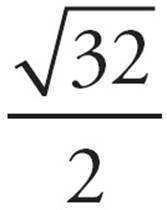= = 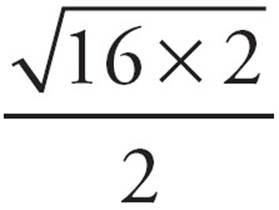= 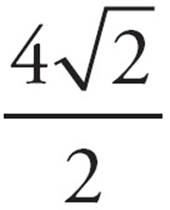2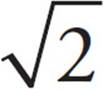. It’s a match, so (D) is correct. You could also solve this algebraically. Multiply both sides by 2 to get 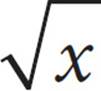= 4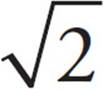. Square both sides to get x = 16 × 2 = 32.

15. CWe’ve got variables in the answer choices, which means this is a perfect Plug In problem. Since we can’t use calculators, let’s make up an easy value for x, such as 2. 9^x + 3^x+1 then becomes 9² + 3²⁺¹ = 81 + 27 = 108. We plugged in x = 2, so let’s use that to find y: y = 3^x, so y = 3² = 9. Now plug in y = 9 to each answer choice to see which one gives you 108. Choice (C) is y(y + 3), which is 9(12) = 108, which is the correct answer.

Algebra Strategies Drill 2: Calculator-Permitted Section

8. CTwo variables tells you this is a great place to plug in. Let’s pick numbers that make the math easy. You can try x = 30 and y = 2. So in 2 hours there are 4 periods of 30 minutes each: 12 × 4 = 48. Alex can fold 48 napkins in 2 hours. 48 is your target. Plugging into your answer choices gives you (C) as the only correct answer.

12. DThis is a perfect question for PITA. The question asks for the greatest possible number of 20-ounce boxes. Start with (B). If there are twenty-five 20-ounce boxes, then there are twenty-five 8-ounce boxes because a total of 50 boxes was purchased. In this case, the twenty-five 20-ounce boxes weigh 500 ounces, and the twenty-five 8-ounce boxes weigh 200 ounces; the total is 700 ounces. This is too big because the question says the total weight was less than 600. If (B) is too big, (A) must also be too big; eliminate both answers. If you try (C), the total weight is 604 ounces, which is still too big. So the answer must be (D).

18. DSince you are never told what x is, and there is no way to find it, plug in for x. Say that x = 100. 63% of 100 is 63, and of 100 is 37.5. The ratio of a to c is . So, 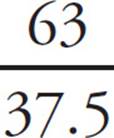= 1.68. To save time, you can ballpark the answer, since a > c and (D) is the only choice greater than 1.

21. DHere’s yet another chance to plug in because of the variables in the answer choices. In this case, you have several variables. You should start by plugging in values for x and y, and then work out c. Because x > y > 0, let’s say x = 6 and y = 3. Therefore, c = + = + = = . The question asks for the value of, which is the reciprocal of, or 2. This is your target answer. If you plug x = 6 and y = 3 into all of the answer choices, you’ll find that only (D) equals 2.

24. BWhen asked for a specific value, try Plugging In the Answers. Label them as gallons of premium and start with the value in (B). If 75 gallons of premium were sold, the station would make 75($2.79) = $209.25 for those sales. A total of 550 gallons was sold, so the station would have sold 550 − 75 = 475 gallons of regular gasoline. The sales for the regular gasoline would be 475($2.39) = $1,135.25. The total sales for both types of gasoline would be $209.25 + $1,135.25 = $1,344.50. That matches the information in the question, so (B) is correct.

25. AVariables in the answer choices? Plug in! This is a percent question, so make k = 100 and d = 40. If 40 out of the 100 gallons have been pumped, that equals 40%. So 40% is your target answer. When you plug k = 100 and d = 40 into the answers, only (A) gives you 40. Plugging In turns a hard question into a much easier question.

Summary

○When an algebra question has numbers in the answer choices, plug each of the numbers in the answer choices into the problem until you find one that works.

○If you start with one of the middle numbers, you may be able to cut your work. The answer choices will be in order, so if your number is too high or too low, you’ll know what to eliminate.

○When the question has variables in the answer choices, you can often plug in your own amounts for the unknowns and do arithmetic instead of algebra.

○When you plug in, use “good” numbers—ones that are simple to work with and that make the problem easier to manipulate: 2, 5, 10, or 100 are generally easy numbers to use.

○Plugging In works on problems containing inequalities, but you will have to be careful and follow some different rules. Plugging in one number is often not enough; to find the answer, you may have to plug in several numbers.

○Not every Plug In question has variables in the answer choices. For some problems, there will be some unknown amount: in that case, try making up a number.

○Plugging In can also be used on Meaning In Context questions. If a question asks you to identify a part of an equation, plug your own amounts into the equation so you can start to see what is going on.