Cracking the GRE Premium (2015)
Part III How to Crack the Math Section
Chapter 10 Numbers and Equations
Numbers and equations form the basis of all the math questions on the GRE. Simply put, the more comfortable you are working with numbers and equations, the easier the math portion of the exam will be. This chapter gives you a review of all the basic mathematical concepts including properties of numbers, factors and multiples, exponents and square roots, and lessons on manipulating and solving equations. This chapter also introduces you to one of The Princeton Review’s key mathematical strategies: Plugging In.
IN THE BEGINNING…
…there were numbers. If you wish to do well on the GRE Math section, you’ll have to be comfortable working with numbers. The concepts tested on the GRE are not exceptionally difficult, but if you are even the least bit skittish about numbers you’ll have a harder time working the problems.
This chapter will familiarize you with all the basics you need to know about numbers and how to work with them. If you’re a mathphobe or haven’t used math in a while, take it slowly and make sure you’re comfortable with this chapter before moving onto the succeeding ones.
You may be a little rusty
when it comes to working
with numbers but you’ll
be surprised at how
quickly you’ll become
comfortable again.
GRE MATH VOCABULARY
Quick—what’s an integer? Is 0 even or odd? How many even prime numbers are there?
Before we go through our techniques for specific types of math problems, we’ll acquaint ourselves with some basic vocabulary and properties of numbers. The GRE loves to test your knowledge of integers, fractions, decimals, and all those other concepts you probably learned years ago. Make sure you’re comfortable with the topics in this chapter before moving on. Even if you feel fairly at ease with number concepts, you should still work through this chapter. ETS is very good at coming up with questions that require you to know ideas forwards and backwards.
The math terms we will review in this section are very simple, but that doesn’t mean they’re not important. Every GRE math question uses simple terms, rules, and definitions. You absolutely need to know this math “vocabulary.” Don’t worry; we will cover only the math terms that youmust know for the GRE.
Learn your vocabulary!
Digits
Digit refers to the numbers that make up other numbers. There are 10 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, and every number is made up of one or more digits. For example, the number 10,897 has five digits: 1, 0, 8, 9, and 7. Each of the digits in a number has its own name, which is designated by a place value. In the number 10,897
· 7 is the ones or units digit.
· 9 is the tens digit.
· 8 is the hundreds digit.
· 0 is the thousands digit.
· 1 is the ten-thousands digit.
Numbers
A number is made up of either a digit or a collection of digits. There are, of course, an infinite number of numbers. Basically, any combination of digits you can imagine is a number, which includes 0, negative numbers, fractions and decimals, and even weird numbers such as 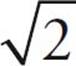 .
.
GRE problems like to try
to trip you up on the
difference between a
number and an integer.
Integers
The integers are the numbers that have no fractional or decimal part, such as –6, –5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5, 6, and so on.
Notice that fractions, such as ![]() , are not integers.
, are not integers.
Remember: Fractions are
NOT integers.
Remember that the number zero is an integer! The values of positive integers increase as they move away from 0 (6 is greater than 5); the values of negative integers decrease as they move away from zero (–6 is less than –5).
PROPERTIES OF NUMBERS AND INTEGERS
Now that you’ve learned the proper names for various types of numbers, let’s look at properties of numbers and integers.
Positive or Negative
Numbers can be positive or negative. Negative numbers are less than zero, while positive numbers are greater than zero. Zero, itself, is neither positive nor negative—all other numbers are either positive or negative.
Even or Odd
Only integers possess the property of being even or odd. Fractions, decimals, and other non-integers cannot be described as even or odd. Integers that are even are those that are divisible by 2; odd integers are those integers that are not divisible by 2. Put another way, even integers have a remainder of 0 when divided by 2 while odd integers have a remainder of 1 when divided by 2.
· Here are some even integers: –4, –2, 0, 2, 4, 6, 8, 10.
· Here are some odd integers: –3, –1, 1, 3, 5, 7, 9, 11.
Zero
Zero is a special little number. It is an integer, but it is neither positive nor negative. However, try to remember these facts about zero:
· 0 is even.
· 0 plus any other number is equal to that other number.
· 0 multiplied by any other number is equal to 0.
· You cannot divide by 0.
Zero has a number of
special properties that are
tested frequently on the
GRE. Technically, zero is a
multiple of every number,
but this fact is rarely
tested on the GRE.
Keep in Mind
· Fractions are neither even nor odd.
· Any integer is even if its units digit is even; any integer is odd if its units digit is odd.
· The results of adding and multiplying odd and even integers are as follows:
○ even + even = even
○ odd + odd = even
○ even + odd = odd
○ even × even = even
○ odd × odd = odd
○ even × odd = even
If you have trouble remembering some of these rules for odd and even, don’t worry. As long as you remember that there are rules, you can always figure them out by plugging in numbers. Let’s say you forget what happens when an odd number is multiplied by an odd number. Just pick two odd numbers, say 3 and 5, and multiply them. 3 × 5 = 15. Now you know: odd × odd = odd.
Be careful: Don’t confuse
odd and even with
positive and negative!
Consecutive Integers
Consecutive integers are integers listed in order of increasing value without any integers missing in between them. Here are some examples:
· 0, 1, 2, 3, 4, 5
· –6, –5, –4, –3, –2, –1, 0
· –3, –2, –1, 0, 1, 2, 3
By the way, fractions and decimals cannot be consecutive, only integers can be consecutive. However, you can have different types of consecutive integers. For example consecutive even integers could be 2, 4, 6, 8, 10. Consecutive multiples of four could be 4, 8, 12, 16.
Absolute Value
The absolute value of a number is equal to its distance from 0 on the number line, which means that the absolute value of any number is always positive, whether the number itself is positive or negative. The symbol for absolute value is a set of double lines: | |. Thus |–5| = 5, and |5| = 5 because both –5 and 5 are a distance of 5 from 0 on the number line.
FACTORS, MULTIPLES, AND DIVISIBILITY
Now let’s look at some ways that integers are related to each other.
Factors
A factor of a particular integer is a number that will divide evenly into the integer in question. For example, 1, 2, 3, 4, 6, and 12 are all factors of 12 because each number divides evenly into 12. In order to find all the factors of a particular integer, write down the factors systematically in pairs of integers that, when multiplied together, make 12, starting with 1 and the integer itself:
· 1 and 12
· 2 and 6
· 3 and 4
If you always start with 1 and the integer itself and work your way up, you’ll make sure you get them all.
Multiples
The multiples of an integer are all the integers for which the original integer is a factor. For example, the multiples of 8 are all the integers of which 8 is a factor: 8, 16, 24, 32, 40 and so on and so on. Note that there are an infinite number of multiples for any given number. Also, zero is a multiple of every number, although this concept is rarely tested on the GRE.
There are only a few
factors of any number;
there are many multiples
of any number.
Prime Numbers
A prime number is an integer that only has two factors: itself and one. Thus, 37 is prime because the only integers that divide evenly into it are 1 and 37, while 10 is not prime because its factors are 1, 2, 5, and 10.
Here is a list of all the prime numbers that are less than 30: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
Here are some other facts about primes that are important to remember:
· 0 is not a prime number.
· 1 is not a prime number.
· 2 is the only even prime number.
· Prime numbers are positive integers. There’s no such thing as a negative prime number or a prime fraction.
1 is not prime!
DIVISIBILITY
An integer is always divisible by its factors. If you’re not sure if one integer is divisible by another, a surefire way to find out is to use the calculator. However, there are also certain rules you can use to determine whether one integer is a factor of another.
· An integer is divisible by 2 if its units digit is divisible by 2. For example, we know just by glancing at it that 598,447,896 is divisible by 2, because the units digit, 6, is divisible by 2.
· An integer is divisible by 3 if the sum of its digits is divisible by 3. For example, we know that 2,145 is divisible by 3 because 2 + 1 + 4 + 5 = 12, and 12 is divisible by 3.
· An integer is divisible by 4 if its last two digits form a number that’s divisible by 4. For example, 712 is divisible by 4 because 12 is divisible by 4.
· An integer is divisible by 5 if its units digit is either 0 or 5. For example, 23,645 is divisible by 5 because its units digit is 5.
· An integer is divisible by 6 if it’s divisible by both 2 and 3. For example, 4,290 is divisible by 6 because it is divisible by 2 (it’s even) and by 3 (4 + 2 + 9 = 15, which is divisible by 3).
· An integer is divisible by 8 if its last three digits form a number that’s divisible by 8. For example, 11,640 is divisible by 8 because 640 is divisible by 8.
· An integer is divisible by 9 if the sum of its digits is divisible by 9. For example, 1,881 is divisible by 9 because 1 + 8 + 8 + 1 = 18, which is divisible by 9.
· An integer is divisible by 10 if its units digit is 0. For example, 1,590 is divisible by 10 because its units digit is 0.
Remainders
If one integer is not divisible by another—meaning that the second integer is not a factor of the first number—you’ll have an integer left over when you divide. This left-over integer is called a remainder; you probably remember working with remainders in grade school.
For example, when 4 is divided by 2, there’s nothing left over so there’s no remainder. In other words, 4 is divisible by 2. You could also say that the remainder is 0.
If a question asks about
a remainder, don’t use
the calculator. Use long
division.
On the other hand, 5 divided by 2 is 2, with 1 left over; 1 is the remainder. Thirteen divided by 8 is 1, with 5 left over as the remainder.
Note that remainders are always less than the number that you are dividing by. For example, the remainder when 13 is divided by 7 is 6. What happens if you divide 14, the next integer, by 7? The remainder is 0.

You can also think of remainders as a measure of distance from the multiples of an integer. For example, 16 is a distance of 2 from 14, which is a multiple of 7. The remainder when 16 is divided by 7 is 2. Note that the ‘distance’ is always measured from the multiple of the number you are dividing by that is less than the integer being divided.
Here’s one more thing to know about remainders. What’s the remainder when 5 is divided by 6? Did you say 0? The remainder is actually 5. Why? Six goes into 5 zero times. What’s left over? 5! When the positive integer you are dividing by is greater than the positive integer you are dividing, the remainder is just the number being divided.
MORE MATH VOCABULARY
In a way, the Math section is almost as much of a vocabulary test as the Verbal section. Below, you’ll find some more standard terms that you should commit to memory before you do any practice problems.
|
Term |
Meaning |
|
sum |
the result of addition |
|
difference |
the result of subtraction |
|
product |
the result of multiplication |
|
quotient |
the result of division |
|
divisor |
the number you divide by |
|
numerator |
the top number in a fraction |
|
denominator |
the bottom number in a fraction |
|
consecutive |
in order from least to greatest |
|
terms |
the numbers and expressions used in an equation |
BASIC OPERATIONS WITH NUMBERS
Now that you’ve learned about numbers and their properties, you’re ready to begin working with them. As we mentioned above, there are four basic operations you can perform on a number: addition, subtraction, multiplication, and division.
Order of Operations
When you work with numbers you can’t just perform the four operations in any way you please. Instead, there are some very specific rules to follow, which are commonly referred to as the order of operations.
It is absolutely necessary that you perform these operations in exactly the right order. In many cases, the correct order will be apparent from the way the problem is written. In cases in which the correct order is not apparent, you need to remember the following mnemonic.
Please Excuse My Dear Aunt Sally, or PEMDAS.
What does PEMDAS stand for?
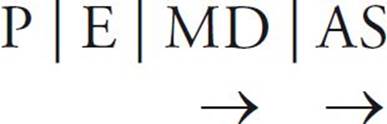
P stands for “parentheses.” Solve anything in parentheses first.
E stands for “exponents.” Solve exponents next. (We’ll review exponents soon.)
M stands for “multiplication” and D stands for “division.” The arrow indicates that you do all the multiplication and division together in the same step, going from left to right.
A stands for “addition” and S stands for “subtraction.” Again, the arrow indicates that you do all the addition and subtraction together in one step, from left to right.
Let’s look at an example:
![]()
12 + 4(2 + 1)2 ÷ 6 − 7 =
Here’s How to Crack It
Start by doing all the math inside the parentheses. 2 + 1 = 3. Now the problem looks like this:
12 + 4(3)2 ÷ 6 − 7 =
Next we have to apply the exponent. 32 = 9. Now this is what we have:
12 + 4(9) ÷ 6 − 7 =
Now we do multiplication and division from left to right. 4 × 9 = 36, and 36 ÷ 6 = 6, which gives us
12 + 6 − 7 =
Finally, we do the addition and subtraction from left to right. 12 + 6 = 18, and 18 − 7 = 11. Therefore,
12 + 4(2 + 1)2 ÷ 6 − 7 = 11
![]()
Multiplication and Division
When multiplying or dividing, keep the following rules in mind:
|
• positive × positive = positive |
2 × 2 = 4 |
|
• negative × negative = positive |
–2 × –2 = 4 |
|
• positive × negative = negative |
2 × –2 = –4 |
|
• positive ÷ positive = positive |
8 ÷ 2 = 4 |
|
• negative ÷ negative = positive |
–8 ÷ –2 = 4 |
|
• positive ÷ negative = negative |
8 ÷ –2 = –4 |
Before taking the GRE, you should have your times tables memorized from 1 through 15. It will be a tremendous advantage if you can quickly and confidently recall that 7 × 12 = 84, for example.
It seems like a small thing,
but memorizing your times
tables will really help you
on test day.
A FEW LAWS
These two basic laws are not necessary for success on the GRE, so if you have trouble with them, don’t worry too much. However, ETS likes to use these laws to make certain math problems more difficult. If you’re comfortable with these two laws, you’ll be able to simplify problems using them, so it’s definitely worth it to use them.
Associative Laws
There are two associative laws—one for addition and one for multiplication. For the sake of simplicity, we’ve lumped them together.
Here’s what you need to know:
When you are adding or multiplying a series of numbers, you can regroup the numbers in any way you’d like.
Here are some examples:
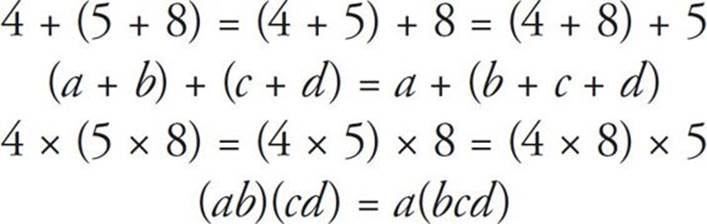
Distributive Law
This is often tested on the GRE. Here’s what it looks like:
a(b + c) = ab + ac
a(b – c) = ab – ac
Here’s an example:
![]()
12(66) + 12(24) = ?
Here’s How to Crack It
This is in the same form as ab + ac. Using the distributive law, this must equal 12(66 + 24), or 12(90) = 1,080.
![]()
EXPONENTS AND SQUARE ROOTS
Exponents and square roots are a popular topic on the GRE. Here’s the information you need to know in order to work with them.

What Are Exponents?
Exponents are a sort of mathematical shorthand for repeated multiplication. Instead of writing (2)(2)(2)(2), you can use an exponent and write 24. The little 4 is the exponent and the 2 is called the base. If you’re stuck on an exponent problem, it’s often helpful to write out the repeated multiplication: When in doubt, expand it out!
There are only five rules for exponents:
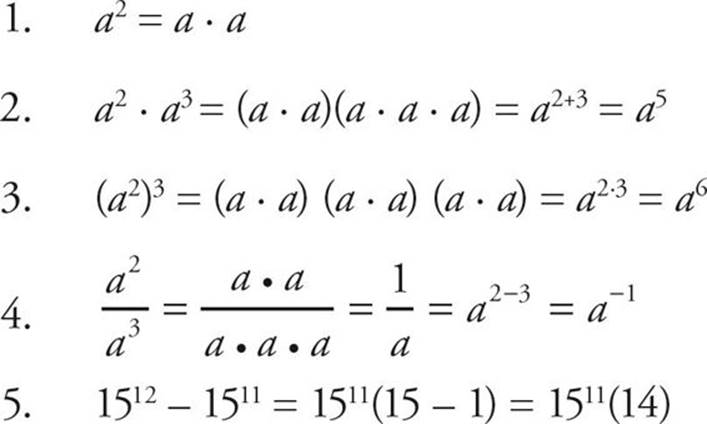
Multiplication with Exponents
It’s simple to multiply two or more numbers that are raised to exponents, as long as they have the same base. In this situation, all you have to do is add the exponents. Consider this example:
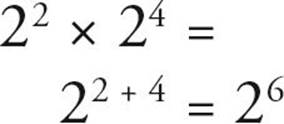
You can see that this is true when you expand it out, which is just as good a way to solve the problem:
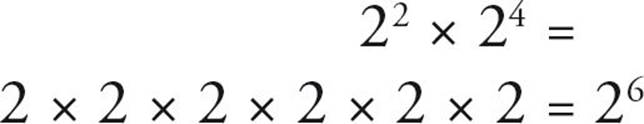
Be careful, though. This rule does not apply to addition. 22 + 24 does not equal 26. There’s no quick and easy method for adding numbers with exponents.
If the numbers have the same bases, however, you can factor. So, 22 + 24 = 22(1 + 22). Note how this operation uses both the distributive law and the multiply-add exponent rule. ETS sometimes writes answers in this factored fashion.
Division with Exponents
Dividing two or more numbers with the same base that are raised to exponents is simple, too. All you have to do is subtract the exponents. Study the following example:
26 ÷ 22 = 26 – 2 = 24
You can see that this is true when you expand it out:
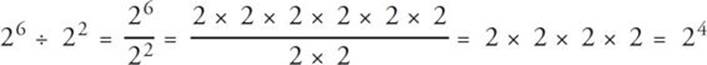
Once again, don’t assume this same shortcut applies to subtraction of numbers with exponents. It doesn’t. So, 26 – 22 does not equal 24. However, you could factor this expression: 26 – 22 = 22(24 – 1). This operation also makes use of both the distributive law and the multiply-add exponent rule. Be on the lookout for ETS to write answers in this fashion sometimes.
Another time you might need to divide with exponents is when you see a negative exponent. In this situation, you just put 1 over the entire expression (in other words, take its reciprocal) and write the negative exponent as a positive exponent. For example,
3–2
gets rewritten as
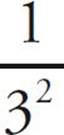
which is
![]()
Exponents to Exponents
When a number with an exponent is raised to another power, you simply multiply the exponents:
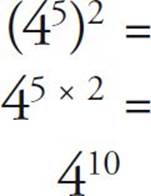
This is what the shorthand notation is really telling us to do:
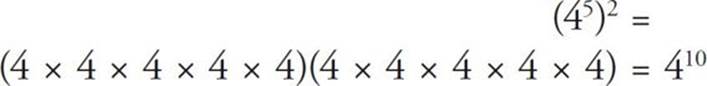
Remember that the exponent applies to everything inside the parentheses. For example, (3x)2 = (3x)(3x) = 9x2, not 3x2 and not 9x. The same is true of fractions raised to exponents: 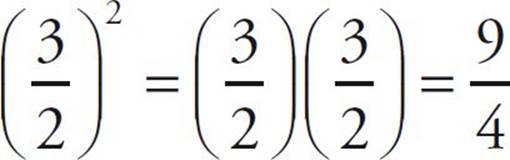 . When working with fractions, remember that the exponent gets applied to both the numerator and the denominator.
. When working with fractions, remember that the exponent gets applied to both the numerator and the denominator.
The Peculiar Behavior of Exponents
· Raising a number greater than 1 to a power greater than 1 results in a bigger number. For example, 22 = 4.
· Raising a fraction that’s between 0 and 1 to a power greater than 1 results in a smaller number. For example, 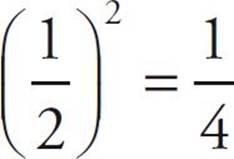 .
.
· A negative number raised to an even power results in a positive number. For example, (–2)2 = 4, because (–2)(–2) = 4.
· A negative number raised to an odd power results in a negative number. For example, (–2)3 = –8, because (–2)(–2)(–2) = –8.
· A number raised to a negative power is equal to the reciprocal of the number raised to the positive power. For example, 2–2 = 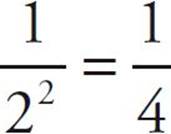
· Any nonzero number raised to the 0 power is 1, no matter what the number is. For example, 1,0000 = 1. Note, however, that 0 to the 0 power is undefined.
· A number raised to the first power ALWAYS results in the number itself. For example, 1,0001 = 1,000.
Here’s an example of a question you might see on the GRE:
![]()
If a ≠ 0, then 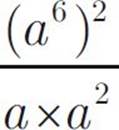 =
=
![]() a5
a5
![]() a6
a6
![]() a7
a7
![]() a8
a8
![]() a9
a9
Always cross off wrong
answer choices on your
scratch paper.
Here’s How to Crack It
In the numerator, we have (a6)2, which is a12. In the denominator, we have a × a2, which is a3. So, a12 ÷ a3 = a9. That’s choice (E).
![]()
Let’s try another—this time, a quant comp:
![]()
|
Quantity A |
Quantity B |
|
274 |
96 |
![]() Quantity A is greater.
Quantity A is greater.
![]() Quantity B is greater.
Quantity B is greater.
![]() The two quantities are equal.
The two quantities are equal.
![]() The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
ALWAYS write down A, B,
C, D for quant comps.
Here’s How to Crack It
Looks scary, huh? But remember what you learned about quant comp problems in the math introduction. Your job is to compare the two quantities, not calculate their values. First of all, eliminate (D)—when only numbers are being compared, the answer can always be determined. Now, as they’re written, we can’t compare these numbers with exponents—they don’t have the same base. But we can fix that. Both 27 and 9 are powers of 3: 27 is 3 × 3 × 3, so 274 is (3 × 3 × 3)4. This equals (3 × 3 × 3) (3 × 3 × 3)(3 × 3 × 3)(3 × 3 × 3), also known as 312. That takes care of Quantity A. In Quantity B, 9 is 3 × 3, so 96 is (3 × 3)6. This equals (3 × 3)(3 × 3)(3 × 3)(3 × 3) (3 × 3)(3 × 3), also known as 312. So, we have 312 in Quantity A and 312 in Quantity B. They’re equal, and the answer is (C).
![]()
What Is a Square Root?
The sign  indicates the square root of a number. For example,
indicates the square root of a number. For example, 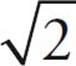 means that some value, times itself (or squared), equals 2. Numbers that have integer square roots, for example,
means that some value, times itself (or squared), equals 2. Numbers that have integer square roots, for example, 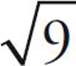 = 3, are known as perfect squares. In this case, 9 is the perfect square.
= 3, are known as perfect squares. In this case, 9 is the perfect square.
If x2 = 16, then x = ±4. You must be especially careful to remember this on quantitative comparison questions. But when ETS asks you for the value of 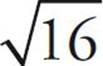 , or the square root of any number, it is asking you for the positive root only. Although squaring –5 will result in 25, just as squaring 5 will, when ETS asks for
, or the square root of any number, it is asking you for the positive root only. Although squaring –5 will result in 25, just as squaring 5 will, when ETS asks for 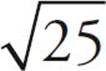 , the only answer it’s looking for is 5.
, the only answer it’s looking for is 5.
Playing with Square Roots
There are rules that allow you to multiply and divide square roots.
You can multiply and
divide any square roots,
but you can add or
subtract roots only when
the number under the
radical sign is the same
To multiply square roots: 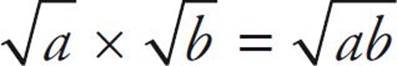
For example, 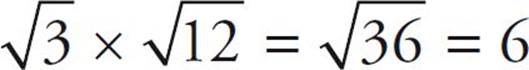
To divide square roots or take the square root of a fraction: 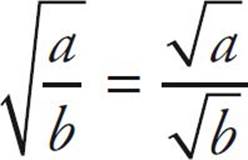
For example, 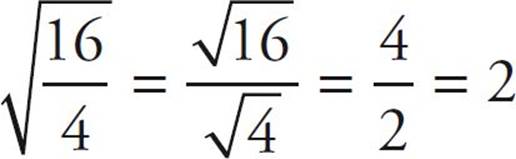
However, you can’t add or subtract square roots unless the roots are the same. So, 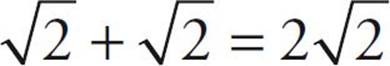 . (Just pretend there’s an invisible 1 in front of the root sign.) But
. (Just pretend there’s an invisible 1 in front of the root sign.) But 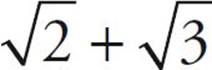 does not equal
does not equal 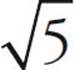 . In order to add different roots, you need to estimate their values first and then add them. We’ll cover how to estimate roots in the pages to come.
. In order to add different roots, you need to estimate their values first and then add them. We’ll cover how to estimate roots in the pages to come.
Here’s an example:
![]()
z2 = 144
|
Quantity A |
Quantity B |
|
z |
|
![]() Quantity A is greater.
Quantity A is greater.
![]() Quantity B is greater.
Quantity B is greater.
![]() The two quantities are equal.
The two quantities are equal.
![]() The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Here’s How to Crack It
You want to pick choice (C), don’t you? After all, if z2 is 144, then the square root of 144 must be z, right? Not so fast. If z2 = 144, then z could be either 12 or –12. But when the radical sign ( ) is used, only the positive root is being referred to. Therefore, Quantity A is equal to 12 or –12, but Quantity B is 12. And that means that (D) is the answer.
) is used, only the positive root is being referred to. Therefore, Quantity A is equal to 12 or –12, but Quantity B is 12. And that means that (D) is the answer.
![]()
Estimating and Simplifying Roots
When you have a perfect square, such as 25 or 36, finding the square root is easy. 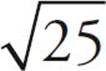 = 5 and
= 5 and 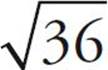 = 6. But what about
= 6. But what about 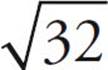 ? You could use the calculator, although that may be too time-consuming. Since 32 is between 25 and 36, you can estimate that
? You could use the calculator, although that may be too time-consuming. Since 32 is between 25 and 36, you can estimate that 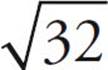 must be between
must be between 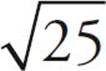 and
and 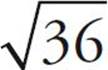 . So
. So 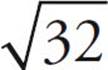 is somewhere between 5 and 6. You also know that 32 is closer to 36 than it is to 25, so
is somewhere between 5 and 6. You also know that 32 is closer to 36 than it is to 25, so 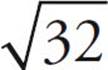 will be closer to 6 than it is to 5, and will probably be about 5.6 or 5.7 (it’s actually 5.66). This process of estimating roots for numbers that aren’t perfect squares can be extremely helpful in eliminating answer choices through Ballparking.
will be closer to 6 than it is to 5, and will probably be about 5.6 or 5.7 (it’s actually 5.66). This process of estimating roots for numbers that aren’t perfect squares can be extremely helpful in eliminating answer choices through Ballparking.
The other thing you might be able to do with a root is simplify it using the rule for multiplying roots. As we’ve seen, 32 isn’t a perfect square, but one of its factors is a perfect square. 32 can be split into 16 × 2, which means that 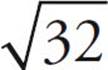 is the same thing as
is the same thing as 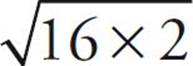 . We can get the square root of 16 and move that outside the square root symbol, giving us 4
. We can get the square root of 16 and move that outside the square root symbol, giving us 4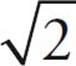 . 4
. 4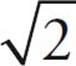 has exactly the same value as
has exactly the same value as 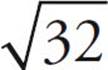 , it’s just written in simpler form. Since, on the GRE, answer choices will nearly always be written in simplest terms, it’s important to know how to do this. Just start by rewriting the number under the radical as a product of two of its factors. As long as at least one of the factors is a perfect square, you’ll be able to simplify the root.
, it’s just written in simpler form. Since, on the GRE, answer choices will nearly always be written in simplest terms, it’s important to know how to do this. Just start by rewriting the number under the radical as a product of two of its factors. As long as at least one of the factors is a perfect square, you’ll be able to simplify the root.
Try the following problem:
![]()

To Simplify Roots:
1. Rewrite the number as
the product of two
factors, one of which is
a perfect square.
2. Use the multiplication
rule for roots.
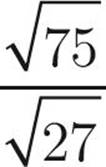 =
=
![]()
![]()
![]()
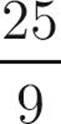
![]()
![]()
![]()
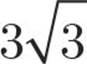
![]()
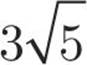
Here’s How to Crack It
First, let’s try to simplify each of these roots. 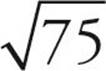 has a factor that is a perfect square—25, so it can be rewritten as
has a factor that is a perfect square—25, so it can be rewritten as 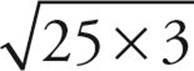 and simplified to
and simplified to 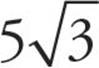 .
. 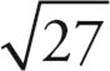 has the perfect square 9 as a factor, so it can be written as
has the perfect square 9 as a factor, so it can be written as 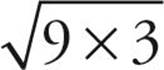 and then simplified to
and then simplified to 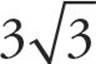 . This means that
. This means that 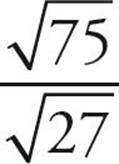 is equal to
is equal to 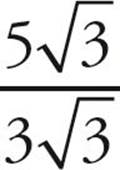 ; the
; the 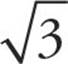 in the numerator and denominator cancel, leaving you with
in the numerator and denominator cancel, leaving you with ![]() . The answer is (A).
. The answer is (A).
![]()
Learn These Four Values
To make calculations of square roots easier, you should memorize the following values. You should be able to recite them without hesitation.
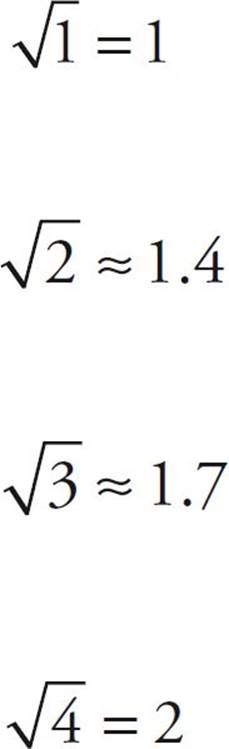
You’ll see them again when we discuss geometry, in Chapter 12.
ALGEBRA: OPERATIONS WITH VARIABLES
Algebra is simply a way of performing operations without numbers; in algebraic expressions, a variable stands in for the unknown number or numbers. While the GRE Math section is not, by and large, an algebra test, you should be comfortable with the basics of working with equations.
Dealing with Variables
Now that you’ve familiarized yourself with number concepts, it’s time to put your knowledge to work. So far, we’ve been showing you how to manipulate numbers, but many GRE math problems involve variables (such as n, x, or y). It’s time to learn how to deal with those.
Manipulating Equations
When working with equations, you can do pretty much anything you want to them as long as you follow the golden rule:
Whatever you do on one side of the equals sign you must also do on the other side.
Solving for One Variable
You can solve equations that have just one variable. In these cases, you start by isolating the variable on one side of the equation and the numbers on the other side. You can do this by adding, subtracting, multiplying, or dividing both sides of the equation by the same number. Just remember that anything you do to one side of an equation, you must do to the other side. Be sure to write down every step. Let’s look at a simple example:
![]()
3x – 4 = 5
Don’t assume you’ll
always need to solve
for the variable on the
GRE; sometimes you’ll
simply have to manipulate
the equation to get the
answer.
Here’s How to Crack It
In this case, you can collect all the constants on the right side of the equation by adding 4 to both sides of the equation. (If you wanted to move the 5 to the left side of the equation, you would subtract 5 from both sides. That’s just how it works.) In general, you can eliminate negative numbers by adding them to both sides of the equation, just as you can eliminate positives by subtracting them from both sides of the equation.
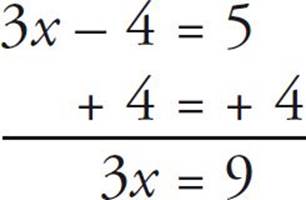
The rule above also applies to numbers in the equation that are divided or multiplied. So in this case, in order to get rid of the 3 that’s multiplied by the variable, x, we need to divide both sides of the equation by 3 to solve for x.
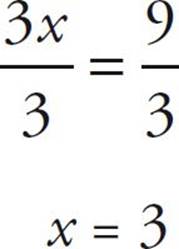
![]()
Let’s try another one:
![]()
5x – 13 = 12 – 20x
Here’s How to Crack It
Again, we want to get all the x values on the same side of the equation:
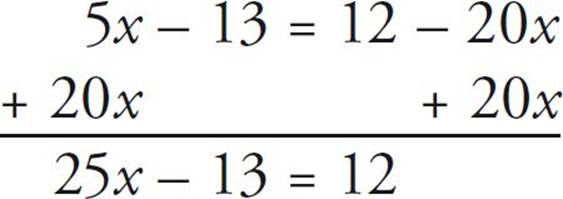
Always write A, B, C, D,
E on your scratch paper
to represent the answer
choices (or A, B, C, D if it’s
quant comp).
Now let’s get rid of that negative 13:
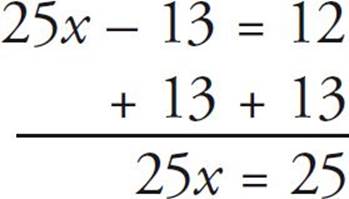
It might be pretty obvious that x is 1, but let’s just finish it:
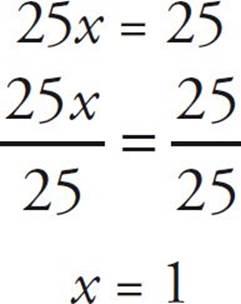
![]()
Let’s try another one:
![]()
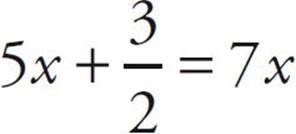
Here’s How to Crack It
First multiply both sides by 2 to get rid of the fraction. (This is called clearing the fraction, by the way, and is a very useful way to start solving an equation that contains fractions.) Remember to multiply all of the terms of the equation!
10x + 3 = 14x
You must always do the
same thing to both sides
of an equation.
Now collect the x’s on the same side:
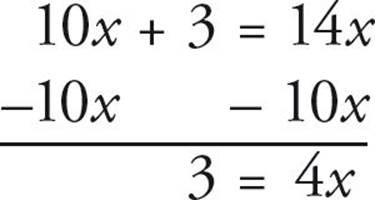
Now finish it up:
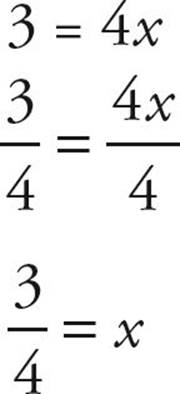
![]()
INEQUALITIES
In an equation, one side is always equal to another. In an inequality, one side of the equation does not equal the other. Equations contain equal signs, while inequalities contain one of the following symbols:
|
≠ |
is not equal to |
|
> |
is greater than |
|
< |
is less than |
|
≥ |
is greater than or equal to |
|
≤ |
is less than or equal to |

The point of the inequality
sign always points to the
smaller value.
You can manipulate any inequality in the same way you can an equation, with one important difference. When you multiply or divide both sides of an inequality by a negative number, the direction of the inequality symbol must change. That is, if x > y, then –x < –y.
To see this rule in action, take a look at this simple inequality:
![]()
12 – 6x > 0
Here’s How to Crack It
You could manipulate this inequality without ever multiplying or dividing by a negative number by just adding 6x to both sides. The sign stays the same. Then divide both sides by positive 6. Again, the sign stays the same.
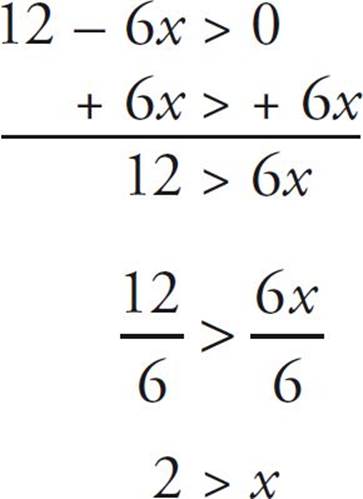
But suppose you subtract 12 from both sides at first:
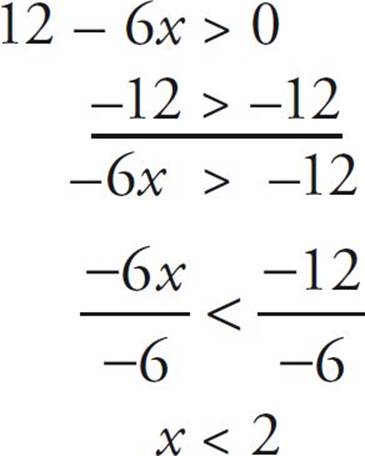
Flip the sign! When you
multiply or divide both
sides of an inequality by
a negative number, the
greater than/less
than sign points the
opposite way.
Notice that the sign flipped because you divided both sides by a negative number. But the answer means the same thing: The first answer says that the number 2 is greater than x, and the second says that x is less than the number 2!
![]()
Sometimes, ETS will give you a range for two variables and then combine them in some way. It looks something like this:
![]()
If 0 ≤ x ≤ 10, and –10 ≤ y ≤ –1, then what is the range for x – y?
Here’s How to Crack It
First, treat the inequality sign like an equal sign. You need all possible combinations of x – y, which means that you need the biggest x minus the biggest y, the biggest x minus the smallest y, the smallest x minus the biggest y, and the smallest x minus the smallest y. There is a simple set-up to do this.
On your scratch paper write the following:
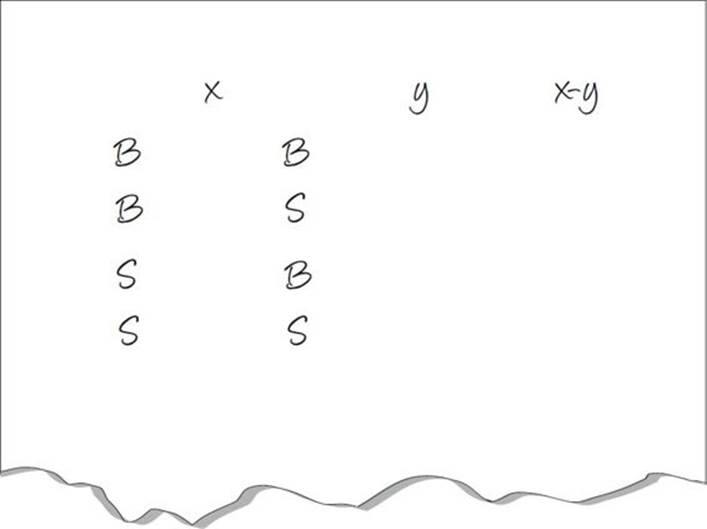
Now just solve for x – y. When you’re done, the biggest and smallest numbers are your answers.

The range for x – y, therefore is 1 ≤ x – y ≤ 20. Check your answer choices and eliminate.
![]()
WORKING WITH TWO VARIABLES
So far we’ve dealt with simple equations that involve only one variable. But on the GRE you’ll sometimes have to deal with equations with two variables. Here’s an example:
![]()
3x + 10y = 64
Here’s How to Crack It
The important thing to note about this situation is that we cannot solve this equation. Why, you ask? The problem is that since there are two variables, there are many possible solutions to this equation all of which are equally valid. For example, the values x = 8 and y = 4 satisfy the equation. But so do the values x = 10 and y = 3.4. In order to solve equations with two variables for a unique solution, we need two equations. Having two equations allows us to find definitive values for our variables.
3x + 10y = 64
6x – 10y = 8

You can’t solve an
equation with two variables
unless you have a
second equation.
When we’re given two equations, we can combine them by adding or subtracting them. We do this so that we can cancel out one of the variables, leaving us with a simple equation with one variable. In this case, it’s easier to add the two equations together:
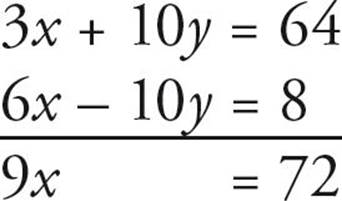
When we add these two equations we get 9x = 72. This is a simple equation which we can solve to find x = 8. Once we’ve done that, we plug that value back into one of the equations and solve for the other variable. For example, if we substitute x = 8 into the first equation, we get 3(8) + 10y= 64, we can solve to find that y = 4.
![]()
Try this one:
![]()
4x + 7y = 41
2x + 3y = 19
Here’s How to Crack It
You might notice that if we add or subtract the two equations, we won’t be left with one variable: Adding the two yields 6x + 10y = 60. That doesn’t help. Subtracting the equations leaves 2x + 4y = 22. No help there, either. In cases like this one, you’ll have to manipulate one of the equations so that subtracting or adding gets rid of one of the variables. In this case, let’s multiply the second equation by 2:
2(2x + 3y) = 2(19)
This gives us the following:
4x + 6y = 38
Now we can subtract this equation from the first equation, yielding y = 3. If we substitute y = 3 into either of the equations we find that x = 5.
![]()
Quadratic Equations
Quadratic equations are special types of equations that involve, as the name suggests, four terms. Here is an example of a quadratic:
(x + 4)(x – 7)
In order to work with quadratics on the GRE, you must be familiar with two concepts: FOIL and factoring.
FOIL
When you see two sets of parentheses, all you have to do is remember to multiply every term in the first set of parentheses by every term in the second set of parentheses. Use FOIL to remember this method. FOIL stands for first, outer, inner, last—the four steps of multiplication. For example, if you see (x + 4) (x + 3), you would multiply the first terms (x × x), the outer terms (x × 3), the inner terms (4 × x), and the last terms (4 × 3), as follows:
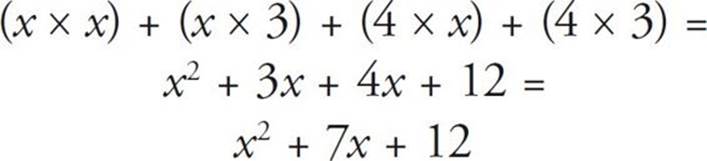
This also works in the opposite direction. For example, if you were given x2 + 7x + 12 = 0, you could solve it by breaking it down as follows:
(x + ) (x + ) = 0
Quadratic Equations
There are quadratic equations that frequently appear on the GRE. You should know them cold, in both their factored and unfactored forms. Here they are:
1. Factored form: x2 – y2 (the difference between two squares)
Unfactored form: (x + y)(x – y)
2. Factored form: (x + y)2
Unfactored form: x2 + 2xy + y2
3. Factored form: (x – y)2
Unfactored form: x2 – 2xy + y2
We know to use plus signs inside the parentheses because both the 7 and the 12 are positive. Now we have to think of two numbers that, when added together, give us 7, and when multiplied together, give us 12. Yep, they’re 4 and 3:
(x + 4) (x + 3) = 0
To find the solutions, set each factor equal to 0 and solve. So, x + 4 = 0 and x + 3 = 0. So x can either be –4 or –3.
Let’s see how this could be used on the GRE:
![]()
If x and y are positive integers, and if x2 + 2xy + y2 = 25, then (x + y)3 =
![]() 5
5
![]() 15
15
![]() 50
50
![]() 75
75
![]() 125
125
Here’s How to Crack It
Problems like this one are the reason you have to memorize those common quadratic equations. The equation in this question is the second expression in the box from the previous page: x2 + 2xy + y2 = (x + y)2. The question tells us that x2 + 2xy + y2 is equal to 25, which means that (x + y)2 is also equal to 25. Think of x + y as one unit that, when squared, is equal to 25. Since this question specifies that x and y are positive integers, what positive integer squared equals 25? Right, 5. So x + y = 5. The question is asking for (x + y)3. In other words, what’s 5 cubed, or 5 × 5 × 5? It’s 125. Choice (E).
![]()
Here’s another one:
![]()
|
Quantity A |
Quantity B |
|
(4 + |
10 |
![]() Quantity A is greater.
Quantity A is greater.
![]() Quantity B is greater.
Quantity B is greater.
![]() The two quantities are equal.
The two quantities are equal.
![]() The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Here’s How to Crack It
First, eliminate choice (D)—we have only numbers here, so the answer can be determined. Now, Quantity A looks like a job for FOIL! Multiply the first terms, and you get 16. Multiply the outer terms and you get –4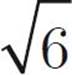 . Multiply the inner terms and you get 4
. Multiply the inner terms and you get 4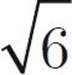 . Multiply the last terms and you get –6. So, we have 16 – 4
. Multiply the last terms and you get –6. So, we have 16 – 4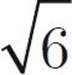 + 4
+ 4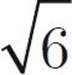 – 6. Those two inner terms cancel each other out, and we’re left with 16 – 6, or 10. What do you know? That’s what we have in Quantity B, too! So, the answer is (C). You might also notice that Quantity A is the first common quadratic from the box on this page: (x + y)(x − y) = x2 − y2. Therefore, (4 +
– 6. Those two inner terms cancel each other out, and we’re left with 16 – 6, or 10. What do you know? That’s what we have in Quantity B, too! So, the answer is (C). You might also notice that Quantity A is the first common quadratic from the box on this page: (x + y)(x − y) = x2 − y2. Therefore, (4 + 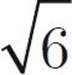 )(4 −
)(4 − 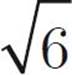 ) = 42 −
) = 42 − 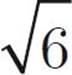 2 = 16 − 6 = 10.
2 = 16 − 6 = 10.
![]()
Factoring
The process of factoring “undoes” the FOIL process. Here is a quadratic in its unfactored, or expanded, form:
x2 – 10x + 24
From this point, we can factor a quadratic by taking the following steps:
1. Separate the x2 into (x )(x ).
2. Find the factors of the third term that, when added or subtracted, yield the second term.
3. Figure out the signs (+/–) for the terms. The signs have to yield the middle number when added and the last term when multiplied.
If we apply these steps to the expression above, we first set up the problem by splitting x2 into
(x )(x )
Next, write down the factors of the third term, 24. The factors are 1 and 24, 2 and 12, 3 and 8, and 4 and 6. Of these pairs of factors, which contains two numbers that we can add or subtract to get the second term, 10? 4 and 6 are the only two that work. That gives us
(x 4)(x 6)
The final step is to figure out the signs. We need to end up with a negative 10 and a positive 24. If we add –6 and –4, we’ll get –10. Similarly, if we multiply –6 and –4, we’ll end up with 24. So the factored form of the expression is
(x – 4)(x – 6)
Solving Quadratic Equations
ETS likes to use quadratic equations because they have an interesting quirk; when you solve a quadratic equation, you usually get not one answer, but two. For this reason, quadratic equations are perfect ways for ETS to try to trick you.
Here’s an example:
![]()
x2 + 2x – 15 = 0
|
Quantity A |
Quantity B |
|
2 |
x |
![]() Quantity A is greater.
Quantity A is greater.
![]() Quantity B is greater.
Quantity B is greater.
![]() The two quantities are equal.
The two quantities are equal.
![]() The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Quadratic equations
usually have two solutions.
Here’s How to Crack It
In order to solve a quadratic equation, the equation must be set equal to zero. Normally, this will already be the case on the GRE, as it is in this example. But if you encounter a quadratic equation that isn’t set equal to zero, you must first manipulate the equation so that it is. Next you must factor the equation; otherwise you cannot solve it. So let’s factor the quadratic equation in this example. We need to figure out the factors of 15 that we can add or subtract to give us 2. The only possible factors are 3 and 5. In order to get a negative 15 and a positive 2, we need to use 5 and –3. So that leaves us
(x – 3)(x + 5) = 0
Next, we’re going to solve each of the two factors within parentheses separately:
x – 3 = 0 and x + 5 = 0
Thus, x = 3 and x = –5. If x = 3, then Quantity B is greater, but if x = –5 then Quantity A is greater. This means that the answer is (D).
![]()
Let’s try another one:
![]()
If x2 + 8x + 16 = 0, then x =

Click on the answer box and type in a number.
Backspace to erase.
Here’s How to Crack It
Let’s factor the equation. Start with (x ) (x ). Next, find the factors of 16 that add or subtract to 8. The factors of 16 are 1 and 16, 2 and 8, and 4 and 4. Of these pairs, only 4 and 4 have a sum of 8. Since we have a positive 8 and a positive 16, the signs for both numbers must be positive. Thus, we end up with (x + 4) (x + 4) = 0. Now, we need to solve the equation. If x + 4 = 0, then x = –4. This is the number we’d enter into the text box on the GRE.
![]()
Simultaneous Equations
ETS will sometimes give you two equations and ask you to use them to find the value of a given expression. Don’t worry; you won’t need any math-class algebra; in most cases, all you will have to do to find ETS’s answer is to add or subtract the two equations.
Here’s an example:
![]()
If 5x + 4y = 6 and 4x + 3y = 5, then what does x + y equal?
Here’s How to Crack It
All you have to do is add the two equations together or subtract one from the other. Here’s what we get when we add them:
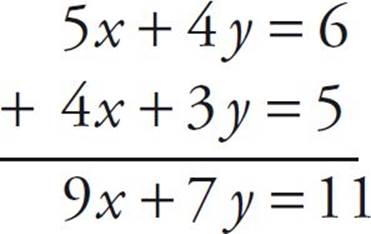
A dead end. So let’s try subtracting them:
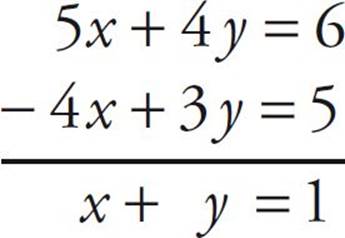
Bingo. The value of the expression (x + y) is exactly what we’re looking for. On the GRE, you may see the two equations written horizontally. Just rewrite the two equations, putting one on top of the other, and then simply add or subtract them.
![]()
PLUGGING IN
Some of the hardest questions you might encounter on the GRE involve algebra. Algebra questions are generally difficult for two reasons. First, they are often complicated, multistep problems. Second, ETS studies the types of mistakes that people make when they solve questions using algebra. They generate wrong answers for the questions based on these common algebraic errors. So, if you aren’t careful, you can make an algebraic mistake and still find your answer among the choices.
Why Plug In?
Plugging In is a powerful tool that can greatly enhance your math score, but you may be wondering why you should plug in when algebra works just fine. Here’s why:
Plugging In converts algebra problems into arithmetic problems. No matter how good you are at algebra, you’re better at arithmetic. Why? Because you use arithmetic every day, every time you go to a store, balance your checkbook, or tip a waiter. Chances are you rarely use algebra in your day-to-day activities.
Plugging In is more accurate than algebra. By Plugging In real numbers, you make the problems concrete rather than abstract. Once you’re working with real numbers, it’s easier to notice when and where you’ve messed up a calculation. It’s much harder to see where you went wrong (or to even know you’ve done something wrong) when you’re staring at a bunch of x’s and y’s.
The GRE allows the use of a calculator. A calculator can do arithmetic but it can’t do algebra, so Plugging In allows you to take advantage of the calculator function.
ETS expects its students to attack the problems algebraically and many of the tricks and the traps built into the problem are designed to catch students who do the problems with algebra. By Plugging In, you’ll avoid these pitfalls.
As you can see, there are a number of excellent reasons for Plugging In. Mastering this technique can have a significant impact on your score.
If you don’t like algebra, you’re in luck. You don’t have to do it. Plugging In will take even the hardest, messiest GRE problem and turn it into a simple arithmetic problem.
Let’s look at an example.
![]()
Dale gives Miranda x bottles of water. He gives Marcella two fewer bottles of water than he gives to Miranda and he gives Mary three more bottles of water than he gives to Marcella. How many bottles of water did Dale give to Miranda, Marcella and Mary, in terms of x ?
![]() 3x – 1
3x – 1
![]() 3x
3x
![]() 3x + 1
3x + 1
![]() 3x + 2
3x + 2
![]() x – 2
x – 2
Here’s How to Crack It
Let’s use an easy number like 10 for the variable. Be sure to write down x = 10 on your scratch paper. So, Miranda gets 10 bottles of water. Marcella gets two fewer bottles of water than Miranda, so Marcella gets 8 bottles. Mary gets three more bottles than Marcella, so Mary gets 11 bottles. That’s a total of 10 + 8 + 11 = 29 bottles of water. Be sure to do the calculations on your scratch paper. Circle 29 (the target answer) and Plug In 10 every time you see an x in the answer choices. Which answer equals 29 when x is 10? Be sure to check all five answers.
(A) 3(10) – 1 = 29 Looks good!
(B) 3(10) = 30 Nope
(C) 3(10) + 1 = 31 Nope
(D) 3(10) + 2 = 32 Nope
(E) 10 – 2 = 8 Nope
Pretty easy compared to the algebra, huh?
![]()
As you can see, Plugging In turned this algebra problem into an arithmetic problem. The best news is that you can solve any problem with variables by using Plugging In.

Here are the steps:
Step 1:
Recognize the opportunity. You can Plug In on any problem that has variables in the answer choices. The minute you see variables in the answers, even before you have read the problem, you know you can Plug In.
Step 2:
Set up your Scratch Paper. You cannot solve Plugging In problems in your head. Even if it seems like an easy question of translating a word problem into an algebraic equation, remember that there are trap answer choices. When a question pops up, the minute you see variables, list your answer choices, A–E, on your scratch paper.
Step 3:
Plug In. If the question asks for “x apples,” come up with a number for x. The goal here is to make your life easier, so Plug In something simple but avoid 1 or 0. If you Plug In a number and the math starts getting difficult (for example, you start getting fractions or negative numbers), don’t be afraid to just change the number you Plug In. Always label each variable on your scratch paper.
Step 4:
Solve for the Target. The Target is the value the problem asks you to solve for. Once you’ve gotten a Target write it down on your scratch paper and circle it.
Step 5:
Check All Answer Choices. Anywhere you see a variable, Plug In the number you have written down for that variable. Do any required math. The correct answer is the one that matches your target number. If more than one answer matches your target number, just Plug In a different number for your variables and test the remaining answer choices.
Can I Just Plug In Anything?
You can Plug In any numbers you like, as long as they’re consistent with any restrictions stated in the problem, but it’s faster if you use easy numbers. What makes a number easy? That depends on the problem. In most cases, smaller numbers are easier to work with than larger numbers. Usually, it’s best to start small, with 2, for example. Avoid 0 and 1; both 0 and 1 have special properties, which you’ll hear more about later. You want to avoid these numbers because they will often make more than one answer choice match the target. For example, if we Plug In 0 for a variable, then the answers 2x, 3x, and 5x would all equal 0. If you avoid these bad number choices, you should also avoid these bad situations. Also, do not Plug In any numbers that show up a lot in the question or answer choices.
Plug In numbers that make
the calculations EASY.
Good Numbers Make Life Easier
Small numbers aren’t always the best choices for Plugging In, though. In a problem involving percentages, for example, 10 and 100 are good numbers to use. In a problem involving minutes or seconds, 30 or 120 are often good choices. You should look for clues in the problem itself to help you choose good numbers.
Always Plug In when
you see variables in the
answer choices!
Let’s work through the following problem, using the Plugging In steps from above:
![]()
Mara has six more than twice as many apples as Robert and half as many apples as Sheila. If Robert has x apples, then, in terms of x, how many apples do Mara, Robert, and Sheila have together?
![]() 2x + 6
2x + 6
![]() 2x + 9
2x + 9
![]() 3x + 12
3x + 12
![]() 4x + 9
4x + 9
![]() 7x + 18
7x + 18
On the GRE, Plugging In
is often safer, and easier,
than doing the algebra.
Here’s How to Crack It
Step 1:
Identify the Opportunity. You’re sitting in your cubicle at the Prometric testing center and this question pops up. What do you see? The variable, x, is in both the question and the answer choices. Good, so what do you do?
Step 2:
Set up your Scratch Paper. On the upper left-hand corner of your scratch paper, list answer choices (A) through (E).
Step 3:
Plug In. The problem tells us that Robert has x apples, so Plug In a number for x. Make it something nice. Try 4. On your scratch paper, write x = 4.
Step 4:
Solve for the Target. The problem tells us that “Mara has six more than twice as many apples as Robert.” If Robert has 4 apples, then Mara must have 14. On your scratch paper, write m = 14. We are also told that Mara has “half as many apples as Sheila.” That means that Sheila must have 28 apples. Write down s = 28. Now, what does the question ask you to find? It asks for the number of apples that Mara, Robert, and Sheila have together. That’s no problem; add the three up to come up with 46 apples. This is your target. Write it down and circle it.
Step 5:
Check All Answer Choices. You can perform only one mathematical function in your head at a time. Anything more than that leads to trouble. For the first answer choice, therefore, you can do 2x in your head; that’s 8, but write down 8 + 6. You don’t need to go any farther than that because this clearly will not add up to 46. Cross off choice (A). Choice (B) gives you 8 + 9. Cross that off. Choice (C) is 12 + 12. This is also too small, so cross it off. Choice (D) gives you 16 + 9. That gets you to 25, which is not your target number, so cross it off. Choice (E) is 28 + 18. Do this on your scratch paper or with the calculator. Do NOT do it in your head. It equals 46, which is your target number. Choice (E) is the correct answer.
(A) 2(4) + 6 = 14—This is not 46, so eliminate it.
(B) 2(4) + 9 = 17—No good either.
(C) 3(4) + 12 = 24—Still not 46.
(D) 4(4) + 9 = 25—This isn’t 46 either.
(E) 7(4) + 18 = 46—Bingo! This is your answer.
![]()
On the GRE, you can Plug In any time the question has variables in the answer choices. You can usually Plug In any number you wish, although you should always pick numbers that will be easy to work with. Some numbers can end up causing more trouble than they’re worth.
When a problem has
variables in the answer
choices, PLUG IN!
When Plugging In, follow these rules:
1. Don’t Plug In 0 or 1. These numbers, while easy to work with, have special properties.
2. Don’t Plug In numbers that are already in the problem; this often leads to more than one answer matching your target.
3. Don’t Plug In the same number for multiple variables. For example, if a problem has x, y, and z in it, pick three different numbers to Plug In for the three variables.
4. Avoid conversion numbers. For example, don’t use 60 for a problem involving hours and minutes.
Finally, Plugging In can be a powerful tool, but you must remember to always check all five answer choices when you plug in. In certain cases, two answer choices can yield the same target. This doesn’t necessarily mean you did anything wrong; you just hit some bad luck. Plug In some new numbers, get a new target and recheck the answers that worked the first time.

Strategy!
The following is a tried-and-true
Princeton Review
strategy (that has nothing
to do with the delicious
type of bread).
PLUGGING IN THE ANSWERS (PITA)
Some questions may not have variables in them but will try to tempt you into using algebra to solve them. We call these Plugging In The Answers, or PITA for short. These are almost always difficult problems. Once you recognize the opportunity, however, they turn into simple arithmetic questions. In fact, the hardest part of these problems is often identifying them as opportunities for PITA. The beauty of these questions is that they take advantage of one of the inherent limitations of a multiple-choice test. ETS has actually given you the answers, and one of them must be correct. In fact, only one can work. The essence of this technique is to systematically Plug In The Answers to see which answer choice works.
Let’s look at an example of a Plugging In The Answers question.
Are you tempted to do
algebra? Are there
numbers in the answer
choices? Plug In The
Answers.
![]()
An office supply store sells binder clips that cost 14 cents and binder clips that cost 16 cents. If a customer purchases 85 binder clips from this store at a total cost of $13.10, how many 14-cent binder clips does the customer purchase?
![]() 16
16
![]() 25
25
![]() 30
30
![]() 35
35
![]() 65
65
Here’s How to Crack It
ETS would like you to solve this problem using algebra. You probably even started to think about the variables you could use to set up some equations to solve this problem. That urge to do algebra is actually the first sign that you can solve this problem using Plugging In The Answers. Other signs that you can Plug In The Answers to solve this problem are that the question asks for a specific amount and that there are numbers in the answer choices. With all these signs, it’s definitely time to Plug In The Answers!
Start by setting up your scratch paper. To do so, just list the five answer choices in a column. Next, label the first column. If you’re going to work with the answer choices, you need to know what they represent. Since the question asks for the number of 14-cent binder clips, you can label this column 14¢.
When you Plug In the Answers, start with answer (C). Since the numbers are always in numerically ascending or descending order, you can cut down on the number of answers that you need to test by starting with answer (C). So, start with the idea that the customer purchased 30 binder clips that cost 14 cents each. What can you figure out with this information? You’d know that the total spent on these binder clips is 30 × $0.14 = $4.20. Make a column with the heading “amount spent” and write $4.20 next to answer (C), 30. Now, look for the next thing you’d know in this scenario. The customer purchased a total of 85 binder clips. So, that means that 55 of the 16-cent binder clips were purchased. Make another column with the heading “16¢” and write 55 in the row for answer (C). Next, make another column for “amount spent” and write 55 × $0.16 = $8.80 in the same row. The next piece of information in the problem is that the customer spends a total of $13.10 on the binder clips. This information allows you to determine if answer (C) is correct. All Plugging In the Answers questions contain a condition like this that lets you decide if the answer is right. In this case, $4.20 + $8.80 = $13.00, which is too small. So, eliminate answer (C). Since the total was too small, more of the binder clips need to cost 16 cents. So, eliminate answers (D) and (E) as well.
Now, do the same steps starting with answer (B). If the customer purchased 25 of the 14-cent binder clips, they cost $3.50. The customer also purchased 60 of the 16-cent binder clips at a cost of $9.60. The total amount spent is $3.50 + $9.60 = $13.10. Since this matches the amount spent in the problem, answer (B) is correct.
Here’s what your scratch paper should look like after this problem:

![]()
Now, here’s a recap of the steps for Plugging In the Answers.
Step 1:
Recognize the Opportunity. There are three ways to do this. The first triggers are the phrases “how much…,” “how many…,” or “what is the value of.…” When you see one of these phrases in a question, you can Plug In The Answers. The second tip-off is specific numbers in the answer choices in ascending or descending order. The last tip-off is your own inclination. If you find yourself tempted to write your own algebraic formulas and to invent your own variables to solve the problem, it’s a sure bet that you can just Plug In The Answer choices.
Step 2:
Set up your Scratch Paper. The minute you recognize the opportunity, list the numbers in the answer choices in a column in the upper left-hand corner of your scratch paper.
Step 3:
Label the First Column. What do these numbers represent? The question asks you to find a specific number. The answer choices are this number. At the top of the column, write down what these numbers represent.
Step 4:
Start with Choice (C). Choice (C) will always be the number in the middle. This the most efficient place to start because it will allow you to eliminate as many as three answer choices if it is wrong.
Step 5:
Create Your Spreadsheet. Use choice (C) to work through the problem. It is always easier to understand the problem using a specific number. Work through the problem in bite-size pieces, and every time you have to do something with the number, make a new column. You can’t have too many columns. Each column is a step in solving the problem.
Step 6:
Rinse and Repeat. On single-answer multiple-choice questions, only one answer choice can work. If choice (C) is correct, you are done. If it is not correct, you may be able to determine if it is too big or too small. If it is too big, you can eliminate it and every answer choice that is bigger. This very quickly gets you down to a 50/50 shot. It also gives you a little spreadsheet specifically designed to calculate the correct answer. When you need to check the remaining answer choices, let the spreadsheet do the thinking for you. All you need to do is to fill in the cells. As soon as you find an answer choice that works, you’re done.
On PITA questions, you can stop once you’ve found the correct answer; you don’t have to check all five answer choices. Just make sure you write EVERYTHING down when doing these questions (and, indeed, all math questions).
PLUGGING IN ON QUANTITATIVE COMPARISON QUESTIONS
Quantitative Comparison questions with variables can be extremely tricky because the obvious answer is often wrong, whereas finding the correct answer may involve a scenario most people would never think of. On the other hand, there is a simple set-up and approach that you can use that ensures that you get these questions right without taking too much time. As always, whenever you see variables, replace them with real numbers. On quant comp questions, however, it is crucial that you Plug In more than once and specifically that you Plug In all of the weird and obscure numbers that you would never use elsewhere. Always keep the nature of the answer choices in mind. Picking choice (A) means that you believe that the quantity in column A will always be bigger—no matter what you Plug In. Choice (B) means that the quantity in column B will always be bigger—no matter what you Plug In, and so forth. To prove that one of these statements is true you have to Plug In every possible number that could change the outcome. Don’t worry. We have a simple process to help figure out what to Plug In and how to track your progress as you do.
Quantitative Comparison
questions often test your
knowledge of the
properties of fractions,
zero, one, negatives, and
other weird numbers.
Here are the steps:
Step 1:
Recognize the Opportunity. The first six, seven, or eight questions of any math section will be quant comp. When a quant comp question pops up and you see variables, you know that you can Plug In.
Step 2:
Set up your Scratch Paper. The minute you see quant comp and variables set up your scratch paper. Your set-up looks like this:
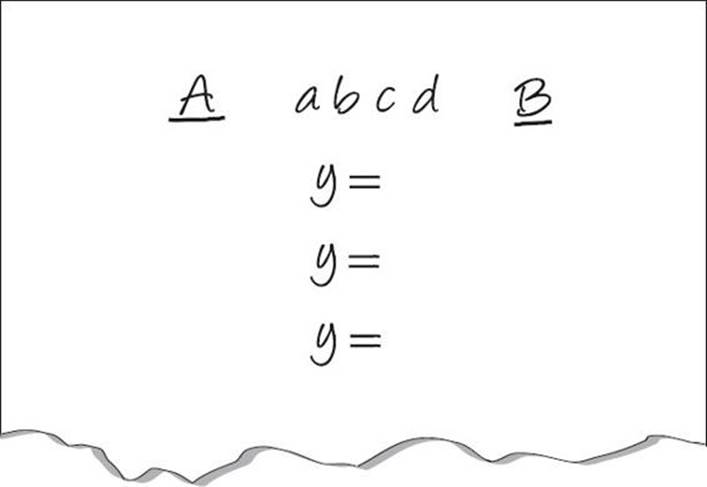
Step 3:
Plug In and Eliminate. Start with a normal number such as 2 or 5 but make sure that you also follow any conditions in the problem. With the number you Plugged In for the variable, calculate the value in Quantity A and write it down. Then calculate the value in Quantity B and write it down. If Quantity A is greater, eliminate choices (B) and (C). If Quantity B is greater, eliminate (A) and (C). If both quantities are the same, eliminate choices (A) and (B). Note that you are already down to a 50/50 shot.
Step 4:
Rinse and Repeat. There are still two answer choices left, so you’re not done yet. The second time you Plug In, you want to try to get a different result. What can you Plug In the second time that messes with the problem? If you’re not sure, use this simple check list: FROZEN. This stands for Fractions, Repeats (numbers from the problem), One, Zero, Extremes (like 100), and Negatives. You won’t always be allowed to Plug In all of these and rarely will you have to. Your goal is to eliminate choices (A), (B), and (C). If you Plug In everything on the checklist and (A), (B), or (C) is still standing, the one that’s still standing is your answer.
The easiest way to solve most quant comp questions that involve variables is to Plug In, just as you would on word problems. But because answer choice (D) is always an option, you always have to make sure it isn’t the answer. So…
Always Plug In at Least Twice in Quant Comp Questions
When you Plug In on Quant Comp questions, you’ll need to Plug In twice because of answer (D). On quant comp questions, it’s not enough to determine whether one quantity is sometimes greater than, less than, or equal to the other; you have to determine whether it always is. If different numbers lead to different answers, then the correct answer is (D). To figure out if one quantity is always greater, you have to Plug In weird numbers to account for all possible situations.

On quant comp, Plug In
“normal” numbers, and
eliminate two choices.
Then Plug In “weird”
numbers (zero, one,
negatives, fractions, or
big numbers) to try to
disprove your first answer.
If different numbers give
you different answers,
you’ve proved that the
answer is (D).
What makes certain numbers weird? They behave in unexpected ways when added, multiplied, or raised to powers. Here are some examples:
· 0 times any number is 0.
· 02 is 0.
· 12 is 1.
· 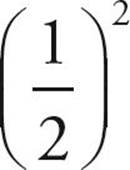 is less than
is less than ![]() .
.
· (–2)(–2) is 4.
· A negative number squared is positive.
· Really big numbers (100, 1,000) can make a really big difference in your answer.
ETS likes to make the correct answer depend on numbers such as these because they know that most test-takers don’t think about these numbers when solving problems.
Here’s how it works:
![]()
|
Quantity A |
Quantity B |
|
2x3 |
4x2 |
![]() Quantity A is greater.
Quantity A is greater.
![]() Quantity B is greater.
Quantity B is greater.
![]() The two quantities are equal.
The two quantities are equal.
![]() The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Here’s How to Crack It
Step 1:
Recognize the Opportunity. First you see quant comp. Second, you see variables. It takes all of three seconds to recognize a quant comp Plug In. You don’t even have to understand the problem at this point. Just recognize the opportunity.
Step 2:
Set up your Scratch Paper. The minute you recognize this as a quant comp Plug In, set up your scratch paper. List “x =” three times down the middle.
Step 3:
Plug In. Let’s start with a normal number like 2. Write down 2 next to your first x. When x = 2, the quantity in column A is 16 (2 • 23), and the quantity in column B is also 16 (4 • 22). Since you have followed the rules and both quantities are the same, neither (A) nor (B) can be the answer. Cross them off. Note that you haven’t worked very hard yet, haven’t spent much time at all, and you are already down to a 50/50 shot.
Step 4:
Rinse and Repeat. Now try something different for x. What if x = 1? The quantity in column A will be 2, and the quantity in column B will be 4. In this case, they are not the same, so choice (C) cannot be the correct answer. Cross it off. Only choice (D) is left, so you’re done.
Here is what your scratch paper should look like:

![]()
You might also have noticed that Plugging In x = 0 would also yield different results. On quant comp questions, ETS hopes you’ll forget to consider what happens when you use numbers such as 0, 1, fractions, and negatives. Therefore, when Plugging In, make sure to use the following FROZEN numbers whenever possible:
Fractions
Repeats
One
Zero
Extremes
Negatives

In your Premium Portal,
you can find a short video
about the proper set up to
maximize efficiency
when using scratch
paper on the GRE.
Make sure you use these numbers aggressively on quant comp problems because they can radically affect the relationship between the two quantities.
Phew. Now we’ve covered the basics of mathematical operations; hopefully a lot of this material came back to you as we went through it, but if not don’t worry! You’ll have plenty of opportunities to refresh your memory of this material as you read through the next two chapters and work the problems you see in the drills.
In the next chapter we’ll look at some everyday math topics that are tested on the GRE, so practice the techniques in the drill that follows, and move on!
Numbers and Equations Drill
Ready to try out your new skills? Give this drill a shot and then check your answers in Part V.
1 of 10
If a prime number, p, is squared and the result is added to the next prime number greater than p, which of the following could be the resulting sum?
Indicate all possible values.
![]() 3
3
![]() 4
4
![]() 7
7
![]() 14
14
![]() 58
58
![]() 60
60
![]() 65
65
![]() 69
69
2 of 10
x2 + 8x = –7
|
Quantity A |
Quantity B |
|
x |
0 |
![]() Quantity A is greater.
Quantity A is greater.
![]() Quantity B is greater.
Quantity B is greater.
![]() The two quantities are equal.
The two quantities are equal.
![]() The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
3 of 10
If 33 × 912 = 3x, what is the value of x ?

Click on the answer box and type in a number.
Backspace to erase.
4 of 10
If A = 2x – (y – 2c) and B = (2x – y) – 2c, then A – B =
![]() –2y
–2y
![]() –4c
–4c
![]() 0
0
![]() 2y
2y
![]() 4c
4c
5 of 10
A merchant sells three different sizes of canned tomatoes. A large can costs the same as 5 medium cans or 7 small cans. If a customer buys an equal number of small and large cans of tomatoes for the same amount of money needed to buy 200 medium cans, how many small cans does she buy?
![]() 35
35
![]() 45
45
![]() 72
72
![]() 199
199
![]() 208
208
6 of 10
If 6k – 5l > 27 and 3l – 2k < –13 and 5k – 5l > j, what is the value of j ?

Click on the answer box and type in a number.
Backspace to erase.
7 of 10
When the integer a is multiplied by 3, the result is 4 less than 6 times the integer b. Therefore, what is a – 2b ?
![]() –12
–12
![]()
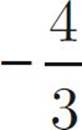
![]()
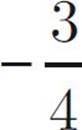
![]()
![]()
![]() 12
12
8 of 10
A bookstore will only order books that come in cases. Each case has 150 books in it and costs $1,757.
|
Quantity A |
Quantity B |
|
The number of books that can be ordered for $10,550 |
The number of books that can be ordered for $12,290 |
![]() Quantity A is greater.
Quantity A is greater.
![]() Quantity B is greater.
Quantity B is greater.
![]() The two quantities are equal.
The two quantities are equal.
![]() The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
9 of 10
If the product of two distinct integers is 91, which of the following could represent the sum of those two integers?
Indicate all possible values.
![]() –92
–92
![]() –91
–91
![]() 7
7
![]() 13
13
![]() 20
20
10 of 10
If x = 3a and y = 9b, then all of the following are equal to 2(x + y) EXCEPT
![]() 3(2a + 6b)
3(2a + 6b)
![]() 6(a + 3b)
6(a + 3b)
![]() 24(
24(![]() a +
a + ![]() b)
b)
![]()
![]() (18a + 54b)
(18a + 54b)
![]() 12(
12(![]() a +
a + ![]() b)
b)
Summary
· Digits are the numbers that make up other numbers. Numbers include whole numbers, fractions, negative numbers, and weird values like the square root of 2. Integers are numbers with no decimal or fractional part.
· Positive numbers are greater than zero and negative numbers less than zero. The number zero is neither positive nor negative.
· Even numbers are divisible by 2; odd numbers aren’t. Only integers can be even or odd.
· A factor divides evenly into an integer. A multiple is an integer that a certain integer is a factor of. Every positive integer is a factor and a multiple of itself.
· The order of operations is PEMDAS.
· An exponent is shorthand for repeated multiplication. When in doubt on exponent problems, expand them out.
· The golden rule of equations: Whatever you do to one side of the equation, you must do to the other.
· With inequalities you have to flip the sign when you multiply or divide by a negative number.
· In order to solve an equation with two variables, you need two equations. Stack them up and add or subtract to cancel out one of the variables.
· Use the FOIL process to expand quadratics. To solve a quadratic equation, set it equal to zero and factor.
· Plugging In converts algebra problems to arithmetic problems. Plug In by replacing variables in the question with real numbers or by working backwards from the answer choices provided.
· Use the FROZEN numbers on tricky quant comp questions with variables.
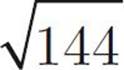
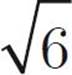 ) (4 –
) (4 –