Cracking the GRE Premium (2015)
Part III How to Crack the Math Section
Chapter 12 Geometry
Chances are you probably haven’t used the Pythagorean theorem recently or had to find the area of a circle in quite a while. However, you’ll be expected to know geometry concepts such as these on the GRE. This chapter reviews all the important rules and formulas you’ll need to crack the geometry problems on the GRE. It also provides examples of how such concepts will be tested on the GRE Math section.
WHY GEOMETRY?
Good question. If you’re going to graduate school for political science or linguistics or history or practically anything that doesn’t involve math, you might be wondering why the heck you have to know the area of a circle or the Pythagorean theorem for this exam. While we may not be able to give you a satisfactory answer to that question, we can help you do well on the geometry questions on the GRE.
Expect to see a handful
of basic geometry
problems on each of
your Math sections.
WHAT YOU NEED TO KNOW
The good news is that you don’t need to know much about actual geometry to do well on the GRE; we’ve boiled down geometry to the handful of bits and pieces that ETS actually tests.
Before we begin, consider yourself warned: Since you’ll be taking your test on a computer screen, you’ll have to be sure to transcribe all the figures onto your scrap paper accurately. All it takes is one mistaken angle or line and you’re sure to get the problem wrong. So make ample use of your scratch paper and always double-check your figures. Start practicing now, by using scratch paper with this book.
Another important thing to know is that you cannot necessarily trust the diagrams ETS gives you. Sometimes they are very deceptive and are intended to confuse you. Always go by what you read, not what you see.
Problem-solving questions
will be drawn to scale
unless they clearly tell you
otherwise. Quant comp
questions, on the other
hand, may not be drawn to
scale, so be on your guard!

DEGREES, LINES, AND ANGLES
For the GRE, you will need to know that
1. A line is a 180-degree angle. In other words, a line is a perfectly flat angle.
2. When two lines intersect, four angles are formed; the sum of these angles is 360 degrees.
3. When two lines are perpendicular to each other, their intersection forms four 90-degree angles. Here is the symbol ETS uses to indicate perpendicular lines: ⊥ .
4. Ninety-degree angles are also called right angles. A right angle on the GRE is identified by a little box at the intersection of the angle’s arms:
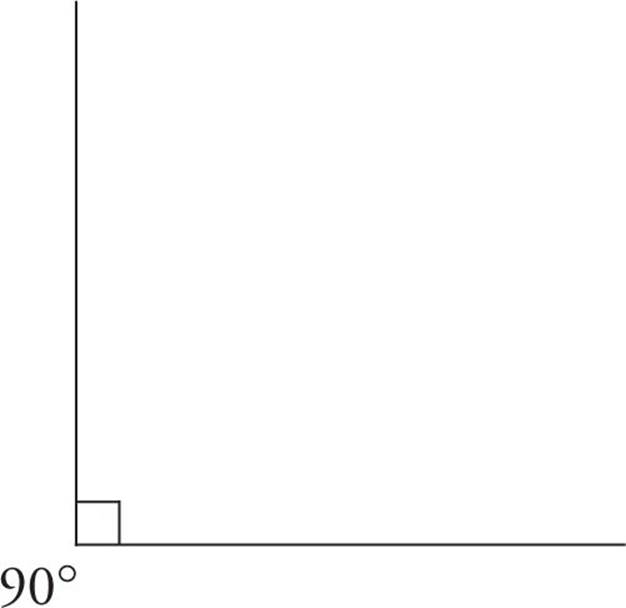
5. The three angles inside a triangle add up to 180 degrees.
6. The four angles inside any four-sided figure add up to 360 degrees.
7. A circle contains 360 degrees.
8. Any line that extends from the center of a circle to the edge of the circle is called a radius (plural is radii).
Vertical Angles
Vertical angles are the angles that are across from each other when two lines intersect. Vertical angles are always equal. In the drawing below, angle x is equal to angle y (they are vertical angles) and angle a is equal to angle b (they are also vertical angles).

On the GRE, the measure
of only one of the vertical
angles is typically shown.
But usually you’ll need
to use the other angle to
solve the problem.
Parallel Lines
Parallel lines are lines that never intersect. When a pair of parallel lines is intersected by a third, two types of angles are formed: big angles and small angles. Any big angle is equal to any big angle, and any small angle is equal to any small angle. The sum of any big angle and any small angle will always equal 180. When ETS tells you that two lines are parallel, this is what is being tested. The symbol for parallel lines and the word parallel are both clues that tell you what to look for in the problem. The minute you see either of them, immediately identify your big and small angles; they will probably come into play.
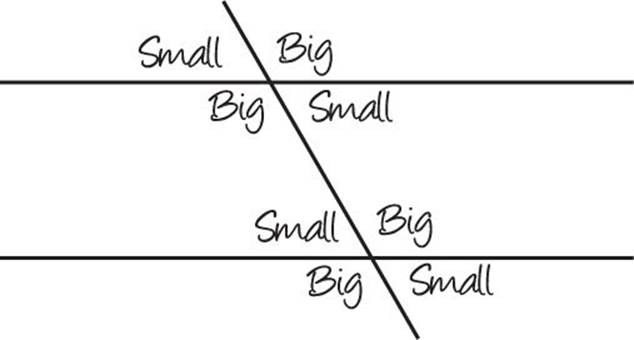
![]()
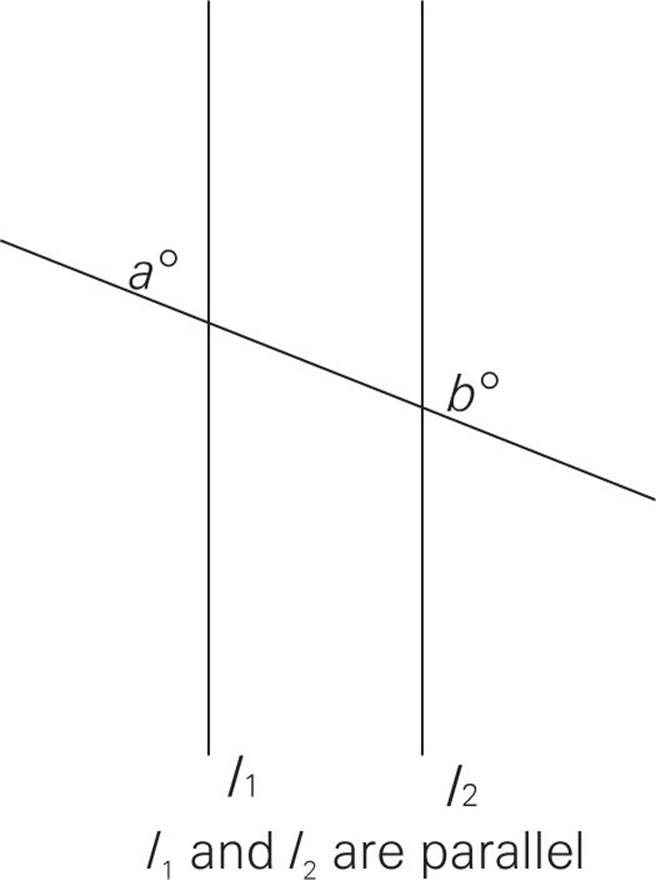
|
Quantity A |
Quantity B |
|
a + b |
180 |
![]() Quantity A is greater.
Quantity A is greater.
![]() Quantity B is greater.
Quantity B is greater.
![]() The two quantities are equal.
The two quantities are equal.
![]() The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Here’s How to Crack It
Notice that you’re told that these lines are parallel. Here’s one very important point: You need to be told that. You can’t assume that they are parallel just because they look like they are.
Okay, so as you just learned, only two angles are formed when two parallel lines are intersected by a third line: a big angle (greater than 90 degrees) and a small one (smaller than 90 degrees). Look at angle a. It looks smaller than 90, right? Now look at angle b. It looks bigger than 90, right? You also know that a + b must add up to 180. The answer is (C).
![]()
TRIANGLES
Triangles are perhaps ETS’s favorite geometrical shape. Triangles have many properties, which make them great candidates for standardized test questions. Make sure you familiarize yourself with the following triangle facts.
Triangles are frequently
tested on the GRE.
The Rule of 180°
Every triangle contains three angles that add up to 180 degrees. You must know this fact cold for the exam. This rule applies to every triangle, no matter what it looks like. Here are some examples:
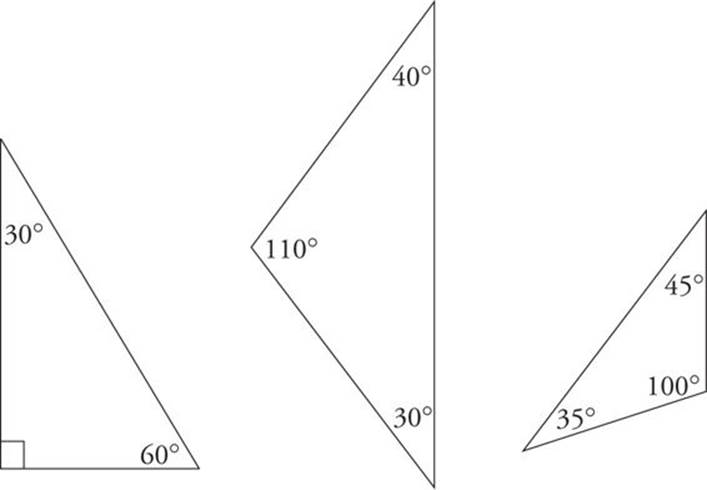
Equilateral Triangles
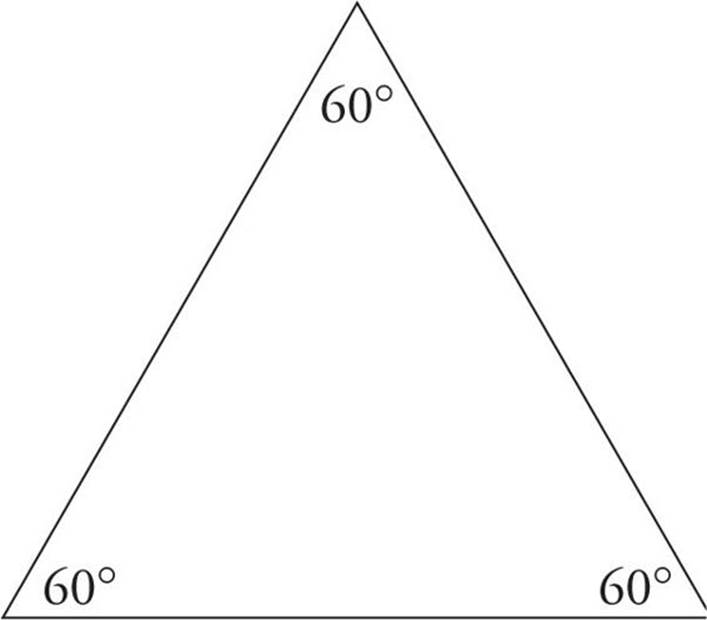
An equilateral triangle is a triangle in which all three sides are equal in length. Because all of the sides are equal in these triangles, all of the angles are equal. Each angle is 60 degrees because 180 divided by 3 is 60.
Isosceles Triangles
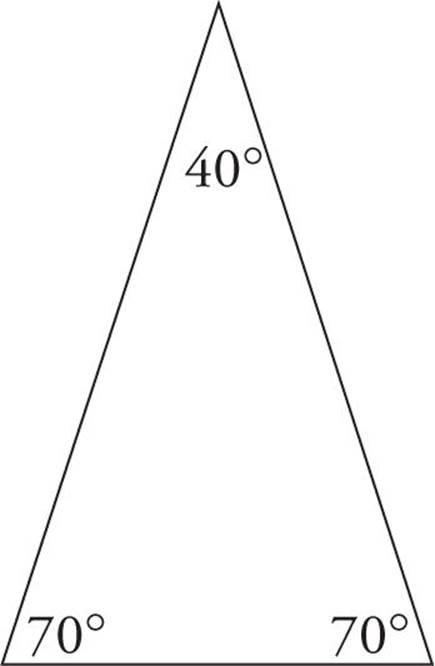
An isosceles triangle is a triangle in which two of the three sides are equal in length. This means that two of the angles are also equal.
Angle/Side Relationships in Triangles
In any triangle, the longest side is opposite the largest interior angle; the shortest side is opposite the smallest interior angle. That’s why the hypotenuse of a right triangle is its longest side—there couldn’t be another angle in the triangle bigger than 90 degrees. Furthermore, equal sides are opposite equal angles.
Perimeter of a Triangle
The perimeter of a triangle is simply a measure of the distance around it. All you have to do to find the perimeter of a triangle is add up the lengths of the sides.
The Third Side Rule
Why is it impossible for the following triangle to exist? (Hint: It’s not drawn to scale.)
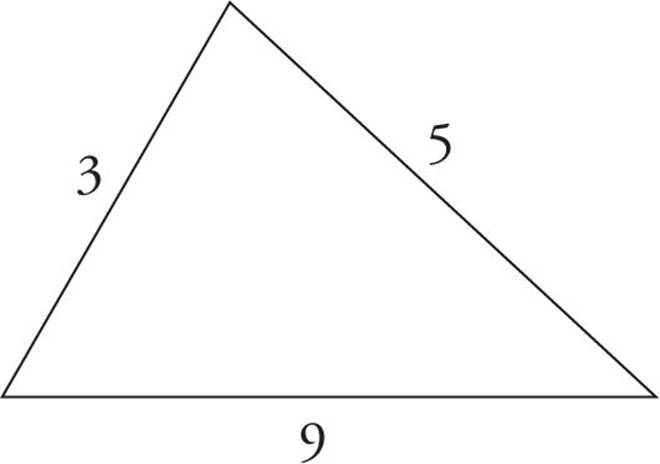
This triangle could not exist because the length of any one side of a triangle is limited by the lengths of the other two sides. This can be summarized by the third side rule:
The length of any one side of a triangle must be less than the sum of the other two sides and greater than the difference between the other two sides.
This rule is not tested frequently on the GRE, but when it is, it’s usually the key to solving the problem. Here’s what the rule means in application: Take the lengths of any two sides of a triangle. Add them together, then subtract one from the other. The length of the third side must lie between those two numbers.
Take the sides 3 and 5 from the triangle above. What’s the longest the third side could measure? Just add and subtract. It could not be as long as 8 (5 + 3) and it could not be as short as 2 (5 – 3).
Therefore, the third side must lie between 2 and 8. It’s important to remember that the third side cannot be equal to either 2 or 8. It must be greater than 2 and less than 8.
Try the following question:
![]()
A triangle has sides 4, 7, and x. Which of the following could be the perimeter of the triangle?
Indicate all such perimeters.
![]() 13
13
![]() 16
16
![]() 17
17
![]() 20
20
![]() 22
22
Here’s How to Crack It
The perimeter of a triangle is equal to the sum of its three sides. So far, we have sides of 4 and 7, so our partial perimeter is 4 + 7 = 11. What about the third side, x? The third-side rule tells us that the side could not be longer than 7 + 4 = 11 or shorter than 7 – 4 = 3. The third side must be greater than 3 and less than 11. Next we add the partial perimeter, 11, to both of these numbers to find the range of the perimeter. 11 + 3 = 14 and 11 + 11 = 22, so the perimeter must be greater than 14 and less than 22. Only choices (A) and (E) fall outside this range. For this question, we have to click on all of the answers that work, so the best answer is (B), (C), and (D).
![]()
Any time you see the
word area or any other
word that indicates that
a formula is to be used,
write the formula on your
scratch paper and park the
information you’re given
directly underneath.
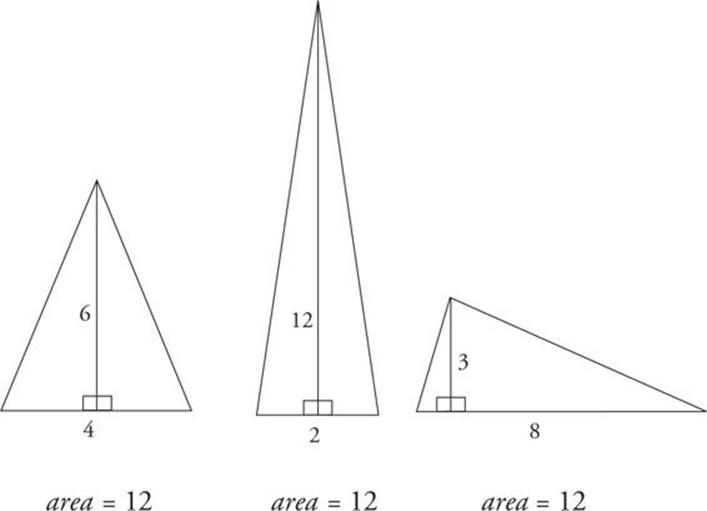
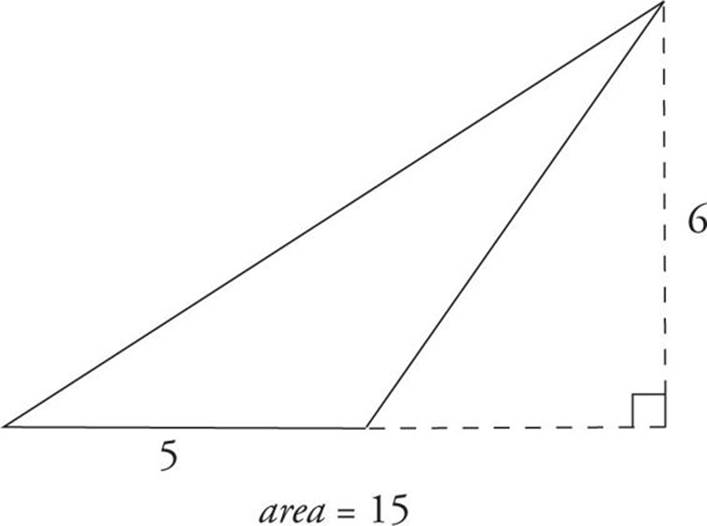
Area of a Triangle
The area of any triangle is equal to its height (or altitude) multiplied by its base, divided by 2, so
A = ![]() bh
bh
The height of a triangle is defined as the length of a perpendicular line drawn from the point of the triangle to its base.
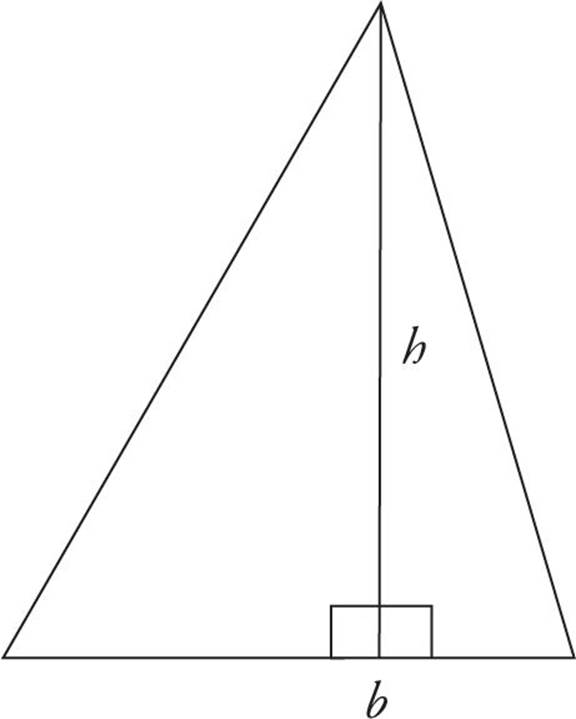
The height of a triangle
must be perpendicular to
the base.
This area formula works on any triangle.
The Pythagorean Theorem
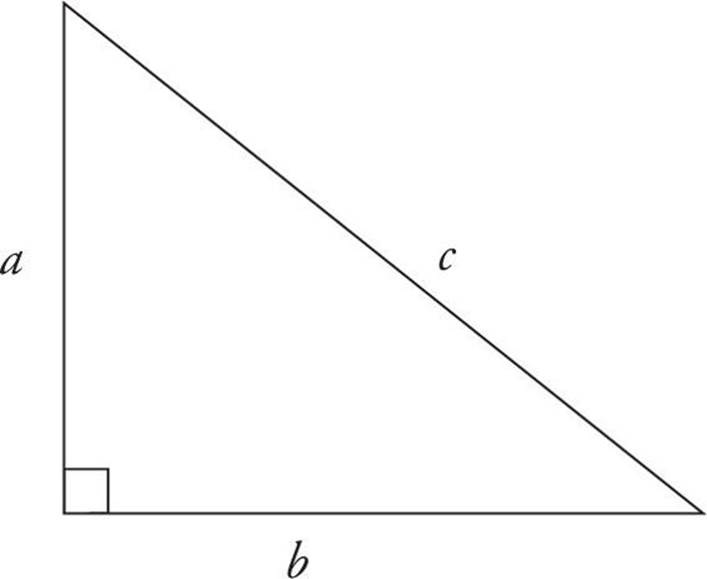
The Pythagorean theorem applies only to right triangles. This theorem states that in a right triangle, the square of the length of the hypotenuse (the longest side, remember?) is equal to the sum of the squares of the lengths of the two other sides. In other words, c2 = a2 + b2, where c is the length of the hypotenuse and a and b are the lengths of the other sides. (The two sides that are not the hypotenuse are called the legs.)
ETS will sometimes try to
intimidate you by using
multiples of the common
Pythagorean triples. For
example, you might see a
10-24-26 triangle. That’s
just a 5-12-13 in disguise
though.
You can always use the Pythagorean theorem to calculate the third side of a right triangle.
Here are the most common right triangles:
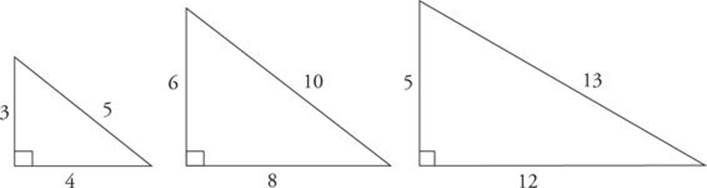
Note that a triangle could have sides with actual lengths of 3, 4, and 5, or 3 : 4 : 5 could just be the ratio of the sides. If you double the ratio, you get a triangle with sides equal to 6, 8, and 10. If you triple it, you get a triangle with sides equal to 9, 12, and 15.
Let’s try an example.
Write everything down on
scratch paper! Don’t do
anything in your head.
![]()
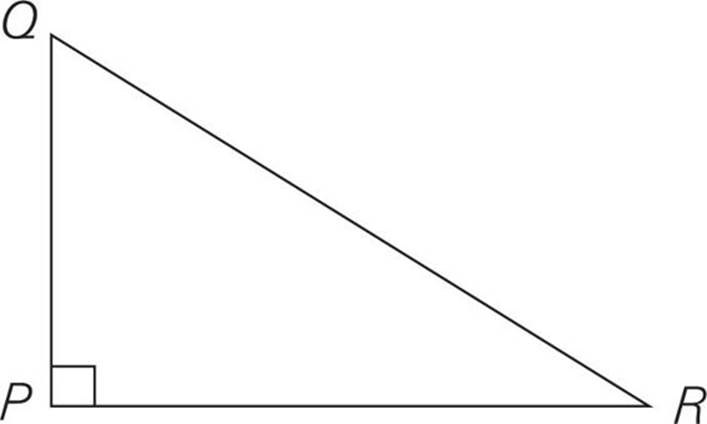
In the figure above, if the distance from point P to point Q is 6 miles and the distance from point Q to point R is 10 miles, what is the distance from point P to point R?
![]() 4
4
![]() 5
5
![]() 6
6
![]() 7
7
![]() 8
8
Here’s How to Crack It
Once you’ve sensitized yourself to the standard right triangles, this problem couldn’t be easier. When you see a right triangle, be suspicious. One leg is 6. The hypotenuse is 10. The triangle has a ratio of 3 : 4 : 5. Therefore, the third side (the other leg) must be 8.
![]()
The Pythagorean theorem will sometimes help you solve problems that involve squares or rectangles. For example, every rectangle or square can be divided into two right triangles. This means that if you know the length and width of any rectangle or square, you also know the length of the diagonal—it’s the shared hypotenuse of the hidden right triangles.
Here’s an example:
![]()
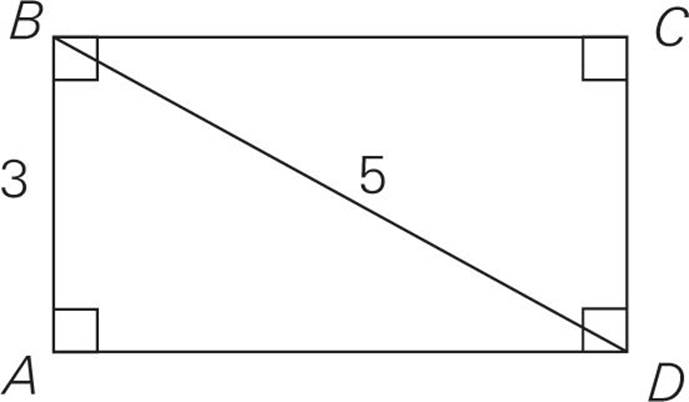
In the rectangle above, what is the area of triangle ABD ?

Click on the answer box and type in a number.
Backspace to erase.
Here’s How to Crack It
We were told that this is a rectangle (remember that you can never assume!), which means that triangle ABD is a right triangle. Not only that, but it’s a 3 : 4 : 5 right triangle (with a side of 3 and a hypotenuse of 5, it must be), with side AD = 4. So, the area of triangle ABD is ![]() the base (3) times the height (4). That’s
the base (3) times the height (4). That’s ![]() of 12, otherwise known as 6. You could enter that value into the box.
of 12, otherwise known as 6. You could enter that value into the box.
![]()
Right Isosceles Triangles
If you take a square and cut it in half along its diagonal, you will create a right isosceles triangle. The two sides of the square stay the same. The 90-degree angle will stay the same, and the other two angles that were 90 degrees each get cut in half and are now 45 degrees. The ratio of sides in a right isosceles triangle is x : x : x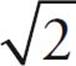 . This is significant for two reasons. First, if you see a problem with a right triangle and there is a
. This is significant for two reasons. First, if you see a problem with a right triangle and there is a 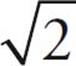 anywhere in the problem, you know what to look for. Second, you always know the length of the diagonal of a square because it is one side times the square root of two.
anywhere in the problem, you know what to look for. Second, you always know the length of the diagonal of a square because it is one side times the square root of two.
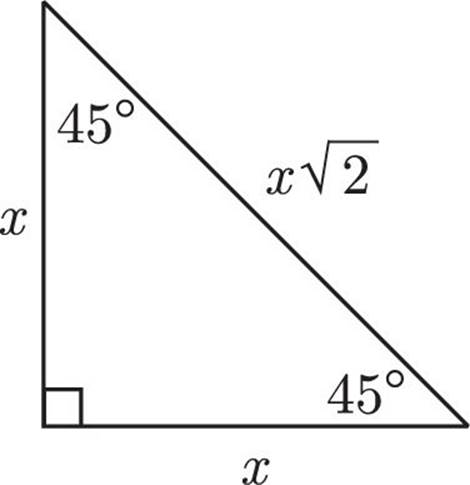

You always know the
length of the diagonal
of a square because it is
one side of the square
times 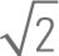 .
.
Let’s try an example involving a special right triangle.
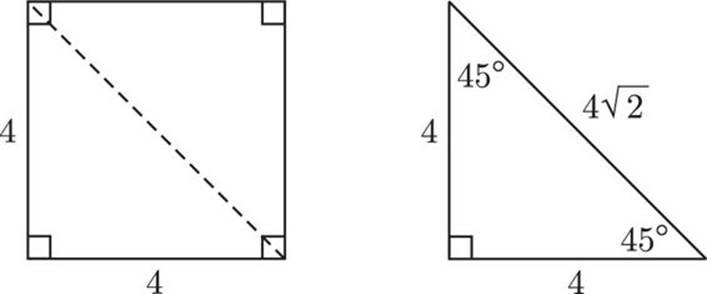
![]()
In the figure above, what is the area of square ABDE ?
![]() 28
28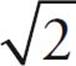
![]() 49
49
![]() 49
49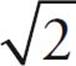
![]() 98
98
![]() 98
98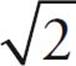
Here’s How to Crack It
In order to figure out the area of square ABDE, we need to know the length of one of its sides. We can get the length of BD by using the isosceles right triangle attached to it. BD is the hypotenuse, which means its length is 7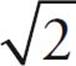 . To get the area of the square we have to square the length of the side we know, or
. To get the area of the square we have to square the length of the side we know, or 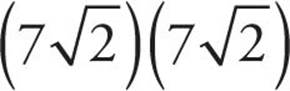 = (49)(2) = 98. That’s choice (D).
= (49)(2) = 98. That’s choice (D).
![]()
30 : 60 : 90 Triangles
If you take an equilateral triangle and draw in the height, you end up cutting it in half and creating a right triangle. The hypotenuse of the right triangle has not changed; it’s just one side of the equilateral triangle. One of the 60 degree angles stays the same as well. The angle where the height meets the base is 90 degrees, naturally, and the side that was the base of the equilateral triangle has been cut in half. The smallest angle, at the top, opposite the smallest side, is 30 degrees. The ratio of sides on a 30 : 60 : 90 triangle is x : x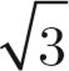 : 2x. Here’s what it looks like:
: 2x. Here’s what it looks like:
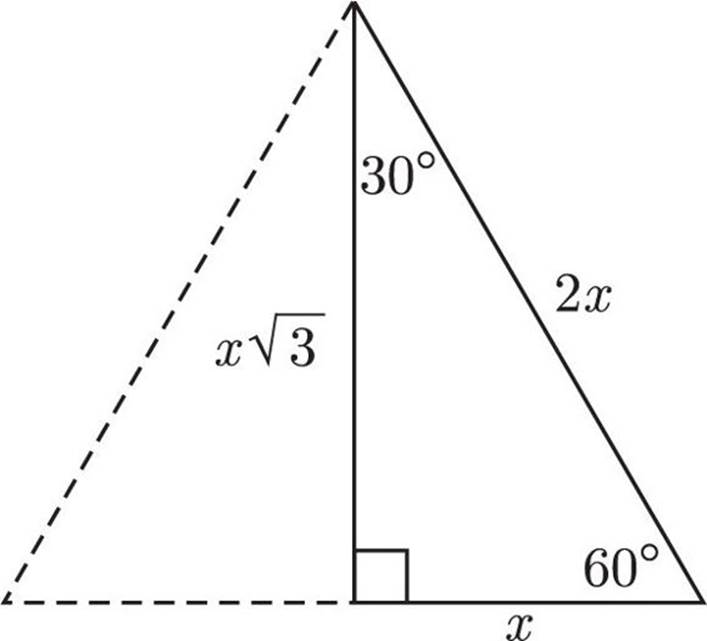
You can always calculate
the area of an equilateral
triangle because you know
that the height is one half
of one side times 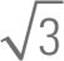 .
.
This is significant for two reasons. The first is that if you see a problem with a right triangle and one side is double the other or there is a 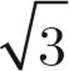 anywhere in the problem, you know what to look for. The second is that you always know the area of an equilateral triangle because you always know the height. The height is one half of one side times the square root of three.
anywhere in the problem, you know what to look for. The second is that you always know the area of an equilateral triangle because you always know the height. The height is one half of one side times the square root of three.
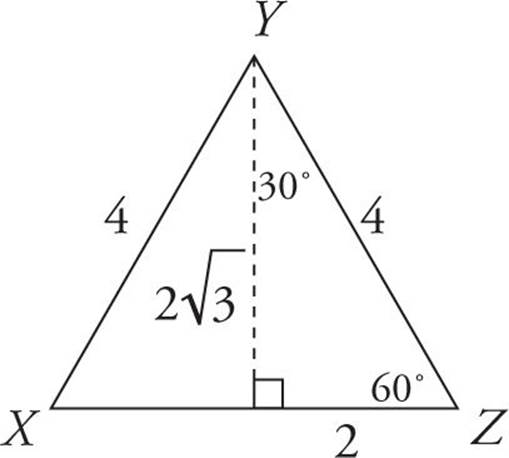
Here’s one more:
![]()
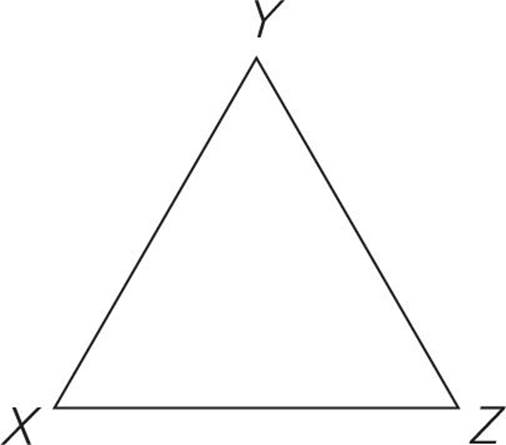
Triangle XYZ in the figure above is an equilateral triangle. If the perimeter of the triangle is 12, what is its area?
![]() 2
2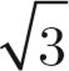
![]() 4
4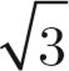
![]() 8
8
![]() 12
12
![]() 8
8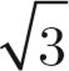
If you see 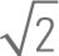 or
or 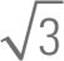 in
in
the answer choices of the
problem it’s a tip-off that
the problem is testing
special right triangles.
Here’s How to Crack It
Here we have an equilateral triangle with a perimeter of 12, which means that each side has a length of 4 and each angle is 60 degrees. Remember that in order to find the area of a triangle, we use the triangle area formula: A = ![]() bh, but first we need to know the base and the height of the triangle. The base is 4, which now gives us A =
bh, but first we need to know the base and the height of the triangle. The base is 4, which now gives us A = ![]() 4h, and now the only thing we need is the height. Remember: The height always has to be perpendicular to the base. Draw a vertical line that splits the equilateral triangle in half. The top angle is also split in half, so now we have this:
4h, and now the only thing we need is the height. Remember: The height always has to be perpendicular to the base. Draw a vertical line that splits the equilateral triangle in half. The top angle is also split in half, so now we have this:
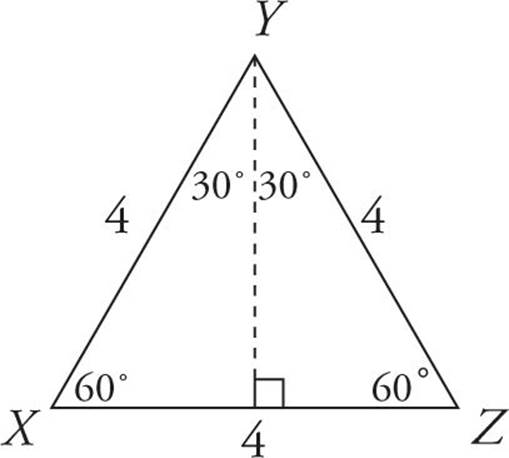
What we’ve done is create two 30 : 60 : 90 right triangles, and we’re going to use one of these right triangles to find the height. Let’s use the one on the right. We know that the hypotenuse in a 30 : 60 : 90 right triangle is always twice the length of the short side. Here we have a hypotenuse (YZ) of 4, so our short side has to be 2. The long side of a 30 : 60 : 90 right triangle is always equal to the short side multiplied by the square root of 3. So if our short side is 2, then our long side must be 2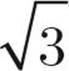 . That’s the height.
. That’s the height.
Finally, we return to our area formula. Now we have A = ![]() × 4 × 2
× 4 × 2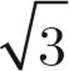 . Multiply it out and you get A = 4
. Multiply it out and you get A = 4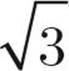 . The answer is (B).
. The answer is (B).
![]()
FOUR-SIDED FIGURES
The four angles inside any figure that has four sides add up to 360 degrees. That includes rectangles, squares, and parallelograms. Parallelograms are four-sided figures made out of two sets of parallel lines whose area can be found with the formula A = bh, where h is the height of a line drawn perpendicular to the base.
Perimeter of a Rectangle
The perimeter of a rectangle is just the sum of the lengths of its four sides.
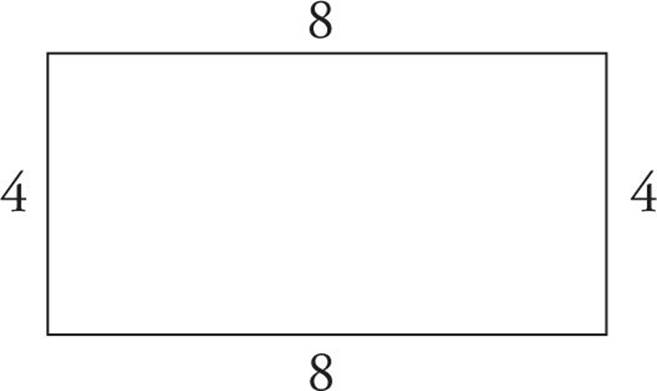
perimeter = 4 + 8 + 4 + 8
The area of a rectangle is equal to its length times its width. For example, the area of the rectangle above is 32 (or 8 × 4).
Area of a Rectangle
The area of a rectangle is equal to its length times its width. For example, the area of the rectangle above is 32 (or 8 × 4).
Squares
A square has four equal sides. The perimeter of a square is, therefore, 4 times the length of any side. The area of a square is equal to the length of any side times itself, or in other words, the length of any side, squared. The diagonal of a square splits it into two 45 : 45 : 90, or isosceles, right triangles.
CIRCLES
Circles are a popular test topic for ETS. There are a few properties that the GRE likes to test over and over again and problems with circles also always seem to use that funny little symbol π. Here’s all you need to know about circles.
The World of Pi
You may remember being taught that the value of pi (π) is 3.14, or even 3.14159. On the GRE, π = 3ish is a close enough approximation. You don’t need to be any more precise than that when doing GRE problems.
What you might not recall about pi is that pi (π) is the ratio between the circumference of a circle and its diameter. When we say that π is a little bigger than 3, we’re saying that every circle is about three times as far around as it is across.
Chord, Radius, and Diameter
A chord is a line that connects two points on the circumference of a circle. The radius of a circle is any line that extends from the center of the circle to a point on the circumference of the circle. The diameter of a circle is a line that connects two points on the circumference of the circle and that goes through the center of the circle. Therefore, the diameter of a circle is twice as long as its radius. Notice as well that the diameter of a circle is also the longest chord and that a radius is not a chord.
The radius is always the
key to circle problems.
Circumference of a Circle
The circumference of a circle is like the perimeter of a triangle: It’s the distance around the outside. The formula for finding the circumference of a circle is 2 times π times the radius, or π times the diameter.
Circumference is
just a fancy way of
saying perimeter.
circumference = 2πr or πd
If the diameter of a circle is 4, then its circumference is 4π, or roughly 12+. If the diameter of a circle is 10, then its circumference is 10π, or a little more than 30.
An arc is a section of the outside, or circumference, of a circle. An angle formed by two radii is called a central angle (it comes out to the edge from the center of the circle). There are 360 degrees in a circle, so if there is an arc formed by, say, a 60-degree central angle, and 60 is ![]() of 360, then the arc formed by this 60-degree central angle will be
of 360, then the arc formed by this 60-degree central angle will be ![]() of the circumference of the circle.
of the circumference of the circle.
Area of a Circle
The area of a circle is equal to π times the square of its radius.
When working with π,
leave it as π in your calculations.
Also, leave 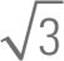 as
as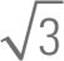 . The answer will have
. The answer will have
them that way.
area = πr2
Let’s try an example of a circle question.
![]()
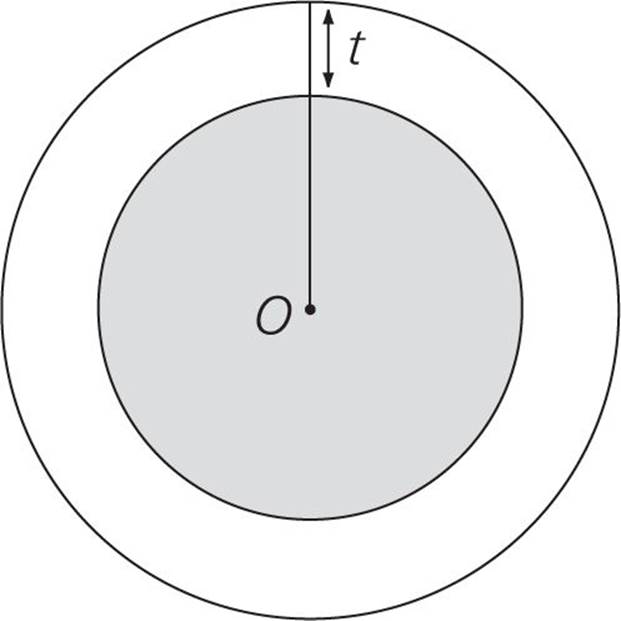
Note: Figure not drawn to scale.
In the wheel above, with center O, the area of the entire wheel is 169π. If the area of the shaded hubcap is 144π, then t =

Click on the answer box and type in a number.
Backspace to erase.
Here’s How to Crack It
We have to figure out what t is, and it’s going to be the length of the radius of the entire wheel minus the length of the radius of the hubcap. If the area of the entire wheel is 169π, the radius is 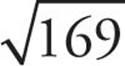 , or 13. If the area of the hubcap is 144π, the radius is
, or 13. If the area of the hubcap is 144π, the radius is 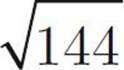 , or 12. 13 – 12 = 1. Enter this value into the box.
, or 12. 13 – 12 = 1. Enter this value into the box.
![]()
Let’s try another one.
![]()
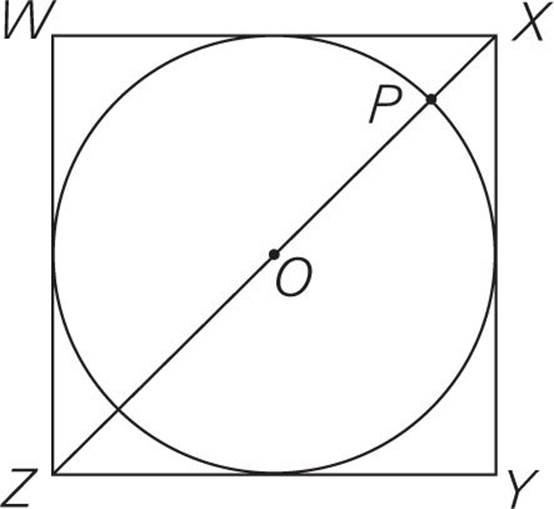
In the figure above, a circle with the center O is inscribed in square WXYZ. If the circle has radius 3, then PZ =
![]() 6
6
![]() 3
3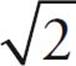
![]() 6 +
6 + 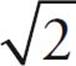
![]() 3 +
3 + 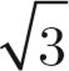
![]() 3
3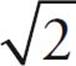 + 3
+ 3
Ballparking answers will
help you eliminate choices.
Here’s How to Crack It
Inscribed means that the edges of the shapes are touching. The radius of the circle is 3, which means that PO is 3. If Z were at the other end of the diameter from P, this problem would be easy and the answer would be 6, right? But Z is beyond the edge of the circle, which means that PZ is a little more than 6. Let’s stop there for a minute and glance at the answer choices. We can eliminate anything that’s “out of the ballpark”—in other words, any answer choice that’s less than 6, equal to 6 itself, or a lot more than 6. Remember when we told you to memorize a few of those square roots?
Let’s use them:
(A) Exactly 6? Nope.
(B) That’s 1.4 × 3, which is 4.2. Too small.
(C) That’s 6 + 1.4, or 7.4. Not bad. Let’s leave that one in.
(D) That’s 3 + 1.7, or 4.7. Too small.
(E) That’s (3 × 1.4) + 3, which is 4.2 + 3, or 7.2. Not bad. Let’s leave that one in, too.
So we eliminated three choices with Ballparking. We’re left with (C) and (E). You could take a guess here if you had to, but let’s do a little more geometry to find the correct answer.
Because this circle is inscribed in the square, the diameter of the circle is the same as a side of the square. We already know that the diameter of the circle is 6, so that means that ZY, and indeed all the sides of the square, are also 6. Now, if ZY is 6, and XY is 6, what’s XZ, the diagonal of the square? Well, XZ is also the hypotenuse of the isosceles right triangle XYZ. The hypotenuse of a right triangle with two sides of 6 is 6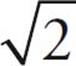 . That’s approximately 6 × 1.4, or 8.4.
. That’s approximately 6 × 1.4, or 8.4.
The question is asking for PZ, which is a little less than XZ. It’s somewhere between 6 and 8.4. The pieces that aren’t part of the diameter of the circle are equal to 8.4 – 6, or 2.4. Divide that in half to get 1.2, which is the distance from the edge of the circle to Z. That means that PZ is 6 + 1.2, or 7.2. Check your remaining answers: Choice (C) is 7.4, and choice (E) is 7.2. Bingo! The answer is (E).
![]()
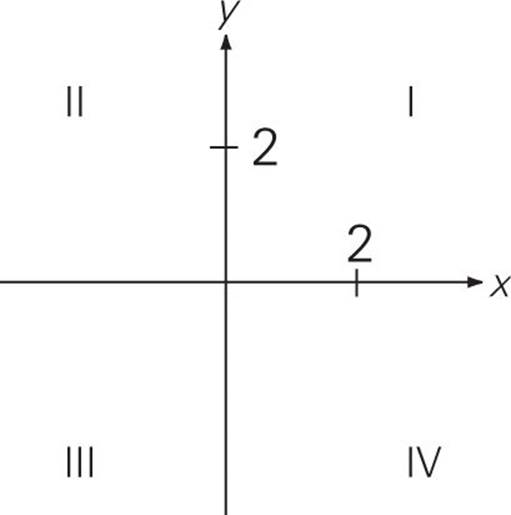
THE COORDINATE SYSTEM
On a coordinate system, the horizontal line is called the x-axis and the vertical line is called the y-axis. The four areas formed by the intersection of these axes are called quadrants. The point where the axes intersect is called the origin. This is what it looks like:

Coordinate geometry
questions often test basic
shapes such as triangles
and squares.
To express any point in the coordinate system, you first give the horizontal value, then the vertical value, or (x, y). In the diagram above, point A can be described by the coordinates (2, 4). That is, the point is two spaces to the right of the origin and four spaces above the origin. Point B can be described by the coordinates (–6, 1). That is, it is six spaces to the left and one space above the origin. What are the coordinates of point C? Right, it’s (–5, –5).
Here’s a GRE example:
![]()
Points (x, 5) and (–6, y), not shown in the figure above, are in quadrants I and III, respectively. If xy ≠ 0, in which quadrant is point (x, y) ?
![]() IV
IV
![]() III
III
![]() II
II
![]() I
I
![]() It cannot be determined from the information given.
It cannot be determined from the information given.
Here’s How to Crack It
If point (x, 5) is in quadrant I, that means x is positive. If point y is in quadrant III, then y is negative. The quadrant that would contain coordinate points with a positive x and a negative y is quadrant IV. That’s answer choice (A).
![]()
Slope
Trickier questions involving the coordinate system might give you the equation for a line on the grid, which will involve something called the slope of the line. The equation of a line is
y = mx + b
In this equation x and y are both points on the line, b stands for the y-intercept, or the point at which the line crosses the y-axis, and m is the slope of the line. Slope is defined as the vertical change divided by the horizontal change, often called “the rise over the run” or the “change in y over the change in x.”
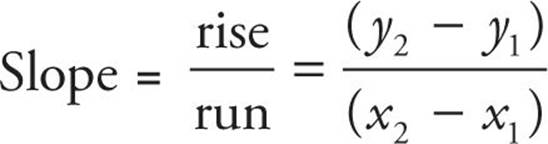
Sometimes on the GRE, m is written instead as a, as in y = ax + b. You’ll see all this in action in a moment.
![]()
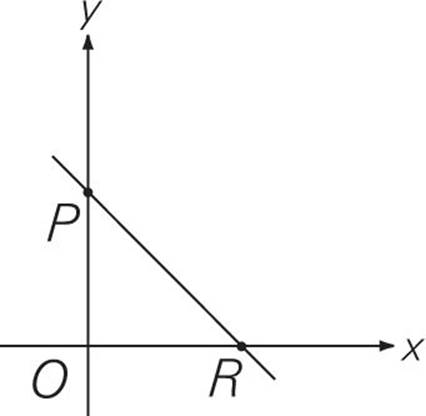
The line y = −![]() x + 1 is graphed on the rectangular coordinate axes.
x + 1 is graphed on the rectangular coordinate axes.
|
Quantity A |
Quantity B |
|
OR |
OP |
![]() Quantity A is greater.
Quantity A is greater.
![]() Quantity B is greater.
Quantity B is greater.
![]() The two quantities are equal.
The two quantities are equal.
![]() The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Here’s How to Crack It
The y-intercept, or b, in this case is 1. That means the line crosses the y-axis at 1. So the coordinates of point P are (0, 1). Now we have to figure out what the coordinates of point R are. We know the y-coordinate is 0, so let’s stick that into the equation (the slope and the y-intercept are constant; they don’t change).
y = mx + b
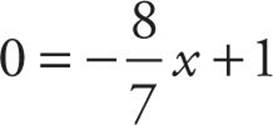
Now let’s solve for x.
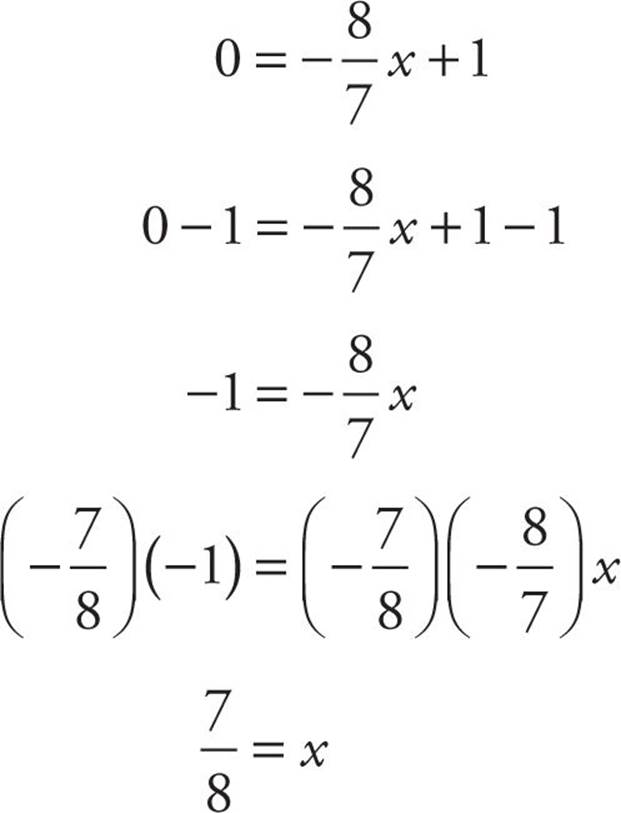
So the coordinates of point R are (![]() , 0). That means OR, in Quantity A, is equal to
, 0). That means OR, in Quantity A, is equal to ![]() , and OP, in Quantity B, is equal to 1. The answer is (B).
, and OP, in Quantity B, is equal to 1. The answer is (B).
Another approach to this question would be to focus on the meaning of slope. Because the slope is −![]() , that means the vertical change is 8 and the horizontal change is 7. In other words, you count up 8 and over 7. Clearly the rise is more than the run; thus OP is more than OR.
, that means the vertical change is 8 and the horizontal change is 7. In other words, you count up 8 and over 7. Clearly the rise is more than the run; thus OP is more than OR.
![]()
Incidentally, if you’re curious about the difference between a positive and negative slope, any line that rises from left to right has a positive slope. Any line that falls from left to right has a negative slope. (A horizontal line has a slope of 0, and a vertical line is said to have “no slope.”)
VOLUME
You can find the volume of a three-dimensional figure by multiplying the area of a two-dimensional figure by its height (or depth). For example, to find the volume of a rectangular solid, you would take the area of a rectangle and multiply it by the depth. The formula is lwh (length × width × height). To find the volume of a circular cylinder, take the area of a circle and multiply by the height. The formula is πr2 times the height (or πr2h).
DIAGONALS IN THREE DIMENSIONS
There’s a special formula that you can use if you are ever asked to find the length of a diagonal (the longest distance between any two corners) inside a three-dimensional rectangular box. It is a2 + b2 + c2 = d2, where a, b, and c are the dimensions of the figure (kind of looks like the Pythagorean theorem, huh?).
Questions that ask about
diagonals are really about
the Pythagorean theorem.
Take a look:
![]()
What is the length of the longest distance between any two corners in a rectangular box with dimensions 3 inches by 4 inches by 5 inches?
![]() 5
5
![]() 12
12
![]() 5
5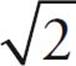
![]() 12
12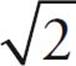
![]() 50
50
Here’s How to Crack It
Let’s use our formula, a2 + b2 + c2 = d2. The dimensions of the box are 3, 4, and 5.
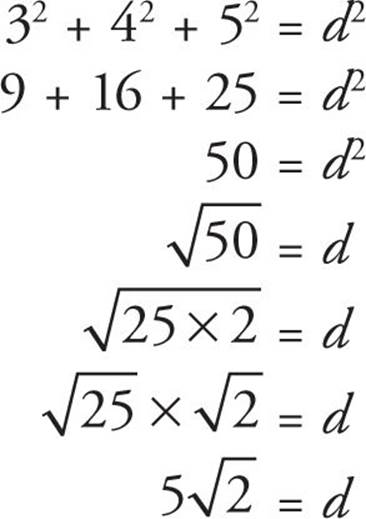
That’s choice (C).
![]()
SURFACE AREA
The surface area of a rectangular box is equal to the sum of the areas of all of its sides. In other words, if you had a box whose dimensions were 2 × 3 × 4, there would be two sides that are 2 by 3 (this surface would have an area of 6), two sides that are 3 by 4 (area of 12), and two sides that are 2 by 4 (area of 8). So, the total surface area would be 6 + 6 + 12 + 12 + 8 + 8, which is 52.
Don’t confuse surface
area with volume.
Key Formulas and Rules
Here is a review of the key rules and formulas to know for the GRE Math section.
Lines and angles
· All straight lines have 180 degrees.
· A right angle measures 90 degrees.
· Vertical angles are equal.
· Parallel lines cut by a third lines have two angles, big angles and small angles. All of the big angles are equal and all of the small angles are equal. The sum of a big angle and a small angle is 180 degrees.
Triangles
· All triangles have 180 degrees.
· The angles and sides of a triangle are in proportion—the largest angle is opposite the largest side and the smallest side is opposite the smallest angle.
· The Pythagorean theorem is c2 = a2 + b2 where c is the length of the hypotenuse.
· The area formula for a triangle is A = 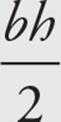 .
.
Quadrilaterals
· All quadrilaterals have 360 degrees.
· The area formula for a squares and rectangles is bh.
Circles
· All circles have 360 degrees.
· The radius is the distance from the center of the circle to any point on the edge.
· The area of a circle is πr2.
· The circumference of a circle is 2πr.
PLUGGING IN ON GEOMETRY PROBLEMS
Remember: Whenever you have a question that has answer choices, like a regular multiple choice or a multiple choice, multiple answer question that has variables in the answer choices, Plug In. On geometry problems, you can Plug In values for angles or lengths as long as the values you Plug In don’t contradict either the wording of the problem or the laws of geometry (you can’t have the interior angles of a triangle add up to anything but 180, for instance).
Here’s an example:
![]()
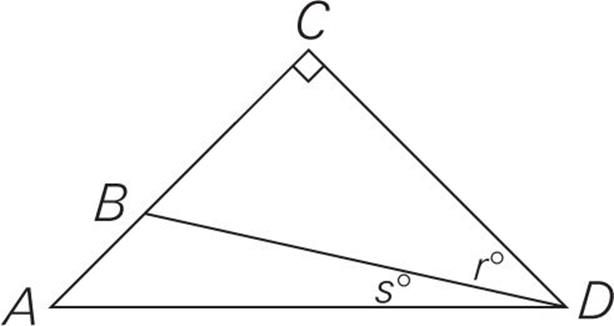
In the drawing above, if AC = CD, then r =
![]() 45 – s
45 – s
![]() 90 – s
90 – s
![]() s
s
![]() 45 + s
45 + s
![]() 60 + s
60 + s
Here’s How to Crack It
See the variables in the answer choices? Let’s Plug In. First of all, we’re told that AC and CD are equal, which means that ACD is an isosceles right triangle. So angles A and D both have to be 45 degrees. Now it’s Plugging In time. The smaller angles, r and s, must add up to 45 degrees, so let’s make r = 40 degrees and s = 5 degrees. The question asks for the value of r, which is 40, so that’s our target answer. Now eliminate answer choices by Plugging In 5 for s.
Don’t forget to Plug In on
geometry questions. Just
pick numbers according to
the rules of geometry.
(A) 45 – 5 = 40. Bingo! Check the other choices to be sure.
(B) 90 – 5 = 85. Nope.
(C) 5. Nope.
(D) 45 + 5 = 50. Eliminate it.
(E) 60 + 5 = 65. No way.
By the way, we knew that the correct answer couldn’t be greater than 45 degrees, because that’s the measure of the entire angle D, so you could have eliminated (D) and (E) right away.
![]()
DRAW IT YOURSELF
When ETS doesn’t include a drawing with a geometry problem, it usually means that the drawing, if supplied, would make ETS’s answer obvious. In cases like this, you should just draw it yourself. Here’s an example:
![]()
|
Quantity A |
Quantity B |
|
The diameter of a circle with area 49π |
14 |
![]() Quantity A is greater.
Quantity A is greater.
![]() Quantity B is greater.
Quantity B is greater.
![]() The two quantities are equal.
The two quantities are equal.
![]() The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Here’s How to Crack It
Visualize the figure. If the area is 49π, what’s the radius? Right: 7. And if the radius is 7, what’s the diameter? Right: 14. The answer is (C).
![]()
Redraw
On tricky quant comp questions, you may need to draw the figure once, eliminate two answer choices, and then draw it another way to try to disprove your first answer and to see if the answer is (D). Here’s an example of a problem that might require you to do this:
For quant comp
geometry questions,
draw, eliminate, and
REDRAW; it’s like
Plugging In twice.
![]()
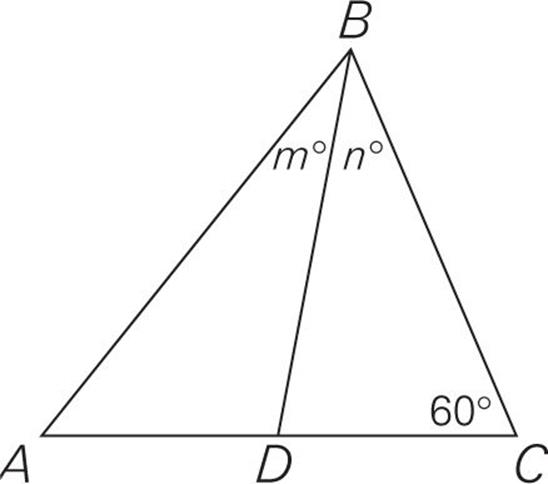
D is the midpoint of AC.
|
Quantity A |
Quantity B |
|
m |
n |
![]() Quantity A is greater.
Quantity A is greater.
![]() Quantity B is greater.
Quantity B is greater.
![]() The two quantities are equal.
The two quantities are equal.
![]() The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Here’s How to Crack It
Are you sure that the triangle looks exactly like this? Nope. We know only what we are told—that the lengths of AD and DC are equal; from this figure, it looks like angles m and n are also equal. Because this means that it’s possible for them to be, we can eliminate choices (A) and (B). But let’s redraw the figure to try to disprove our first answer.
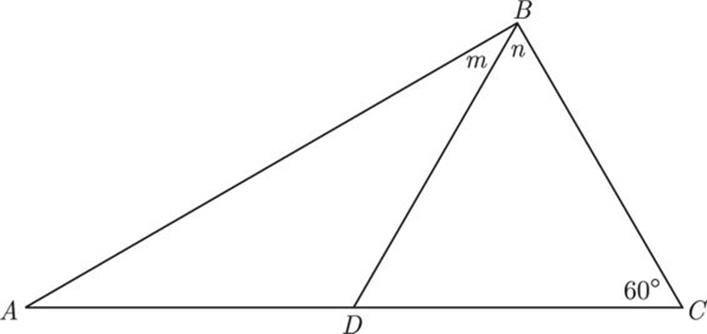
Try drawing the triangle as stretched out as possible. Notice that n is now clearly greater than m, so you can eliminate (C), and the answer is (D).
![]()
Geometry Drill
Think you have mastered these concepts? Try your hand at the following problems and check your work after you have finished. You can find the answers in Part V.
1 of 15
Which of the following could be the degree measures of two angles in a right triangle?
Indicate all such angles.
![]() 20° and 70°
20° and 70°
![]() 30° and 60°
30° and 60°
![]() 45° and 45°
45° and 45°
![]() 55° and 55°
55° and 55°
![]() 75° and 75°
75° and 75°
2 of 15
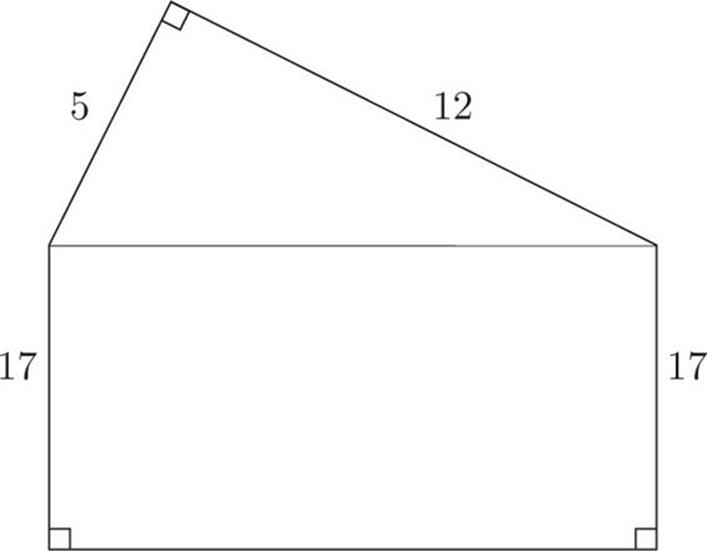
What is the perimeter of the figure above?
![]() 51
51
![]() 64
64
![]() 68
68
![]() 77
77
![]() 91
91
3 of 15
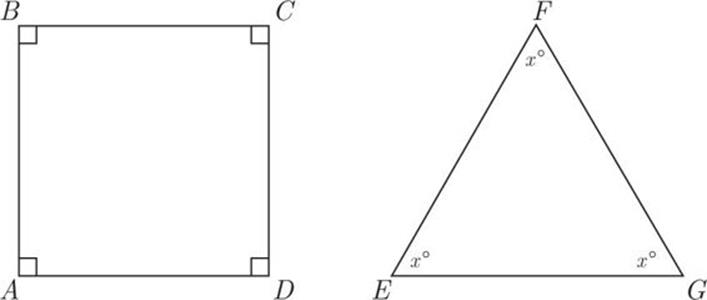
AB = BC = EG
FG = 8
|
Quantity A |
Quantity B |
|
The area of square ABCD |
32 |
![]() Quantity A is greater.
Quantity A is greater.
![]() Quantity B is greater.
Quantity B is greater.
![]() The two quantities are equal.
The two quantities are equal.
![]() The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
4 of 15
(a, 6) is a point (not shown) in quadrant I.
(–6, b) is a point (not shown) in quadrant II.
|
Quantity A |
Quantity B |
|
a |
b |
![]() Quantity A is greater.
Quantity A is greater.
![]() Quantity B is greater.
Quantity B is greater.
![]() The two quantities are equal.
The two quantities are equal.
![]() The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
5 of 15
A piece of twine with length of t is cut into two pieces. The length of the longer piece is 2 yards greater than 3 times the length of the shorter piece. Which of the following is the length, in yards, of the longer piece?
![]()
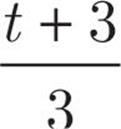
![]()
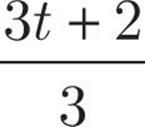
![]()
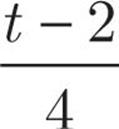
![]()
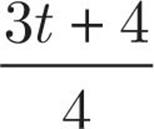
![]()
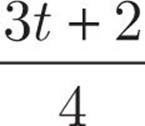
6 of 15
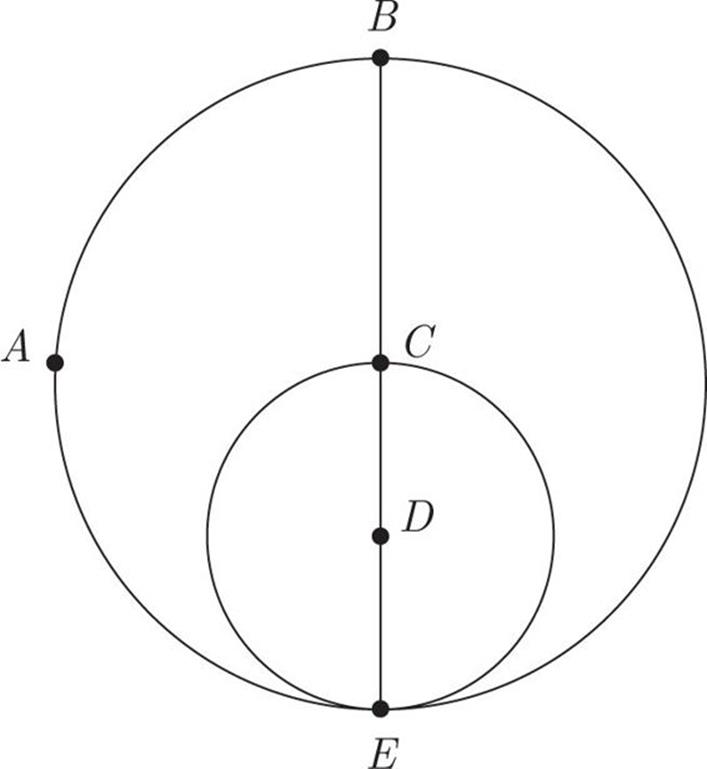
The circle with center D is drawn inside the circle with center C, as shown in the figure above. If CD = 3, what is the area of semicircle EAB ?
![]()
![]() π
π
![]() 9π
9π
![]() 12π
12π
![]() 18π
18π
![]() 36π
36π
7 of 15
For the final exam in a scuba diving certification course, Karl navigates from one point in a lake to another. Karl begins the test x meters directly beneath the boat and swims straight down toward the bottom of the lake for 8 meters. He then turns to his right and swims in a straight line parallel to the surface of the lake and swims 24 meters, at which point he swims directly from his location, in a straight line, back to the boat. If the distance that Karl swims back to the boat is 26 meters, what is the value of x ?
 meters
meters
Click on the answer box and type in a number.
Backspace to erase.
8 of 15
|
Quantity A |
Quantity B |
|
The circumference of a circular region with radius r |
The perimeter of a square with side r |
![]() Quantity A is greater.
Quantity A is greater.
![]() Quantity B is greater.
Quantity B is greater.
![]() The two quantities are equal.
The two quantities are equal.
![]() The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
9 of 15
Triangle ABC is contained within a circle with center C. Points A and B lie on the circle. If the area of circle C is 25π, and the measure of angle ACB is 60°, which of the following are possible lengths for side AB of triangle ABC ?
Indicate all such lengths.
![]() 3
3
![]() 4
4
![]() 5
5
![]() 6
6
![]() 7
7
10 of 15
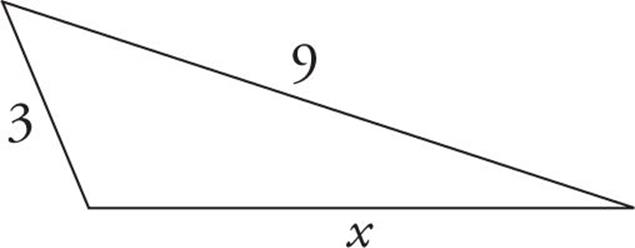
|
Quantity A |
Quantity B |
|
x |
5.9 |
![]() Quantity A is greater.
Quantity A is greater.
![]() Quantity B is greater.
Quantity B is greater.
![]() The two quantities are equal.
The two quantities are equal.
![]() The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
11 of 15
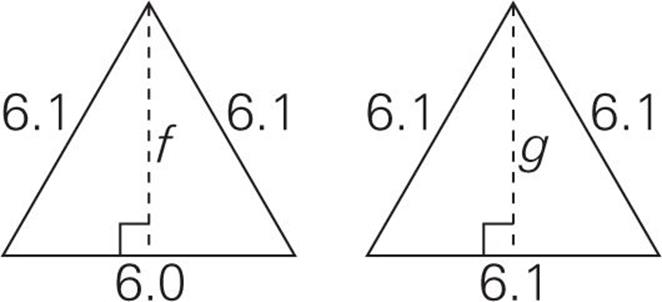
|
Quantity A |
Quantity B |
|
f |
g |
![]() Quantity A is greater.
Quantity A is greater.
![]() Quantity B is greater.
Quantity B is greater.
![]() The two quantities are equal.
The two quantities are equal.
![]() The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
12 of 15
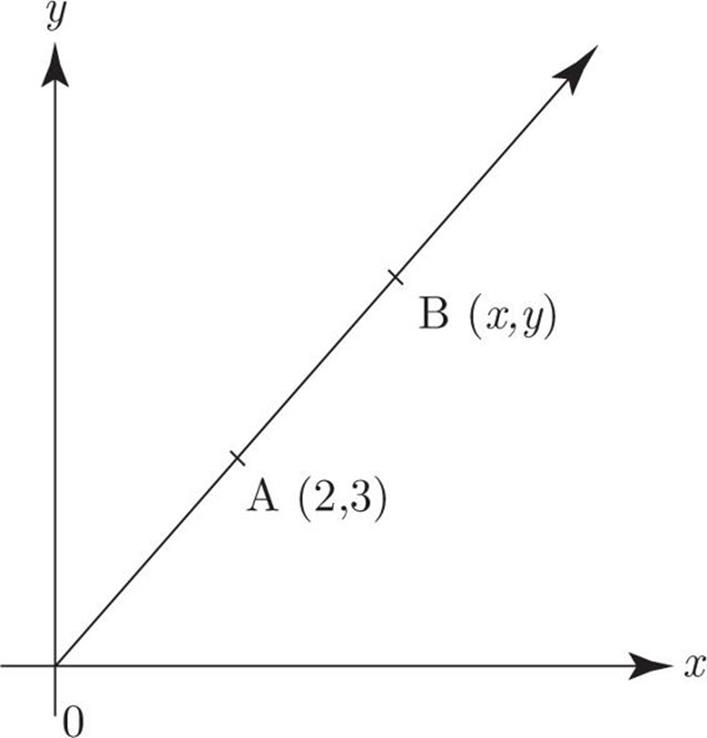
Given points A(2, 3) and B(x, y) in the rectangular coordinate system above, if y = 4.2, then x =
![]() 2.6
2.6
![]() 2.8
2.8
![]() 2.9
2.9
![]() 3.0
3.0
![]() 3.2
3.2
13 of 15
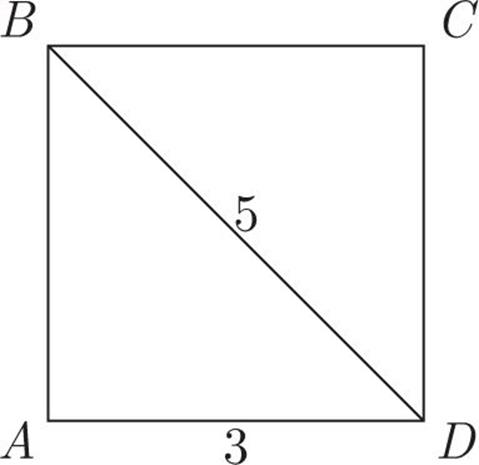
In rectangle ABCD above, which of the following is the area of the triangle ABD ?
![]() 6
6
![]() 7.5
7.5
![]() 10
10
![]() 12
12
![]() 15
15
14 of 15
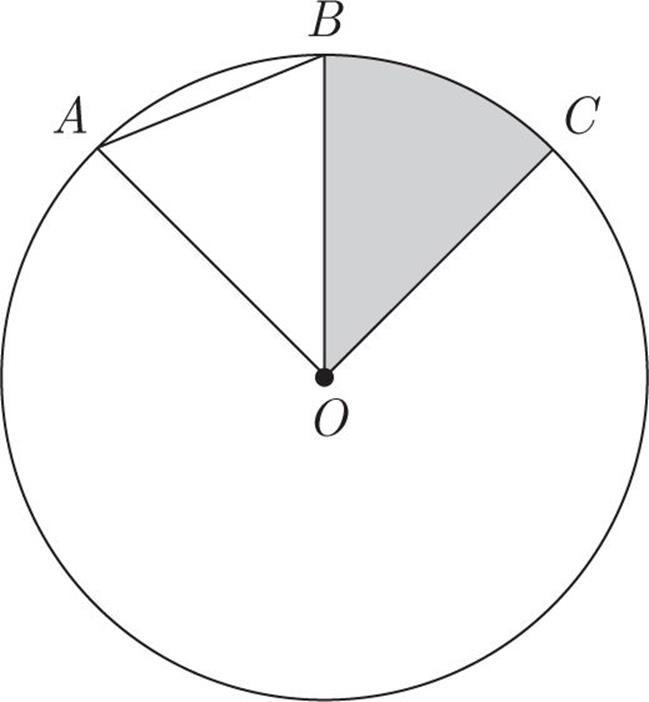
The circle above has a center O.
∠AOB = ∠BOC
|
Quantity A |
Quantity B |
|
The area of triangle AOB |
The area of the shaded region |
![]() Quantity A is greater.
Quantity A is greater.
![]() Quantity B is greater.
Quantity B is greater.
![]() The two quantities are equal.
The two quantities are equal.
![]() The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
15 of 15
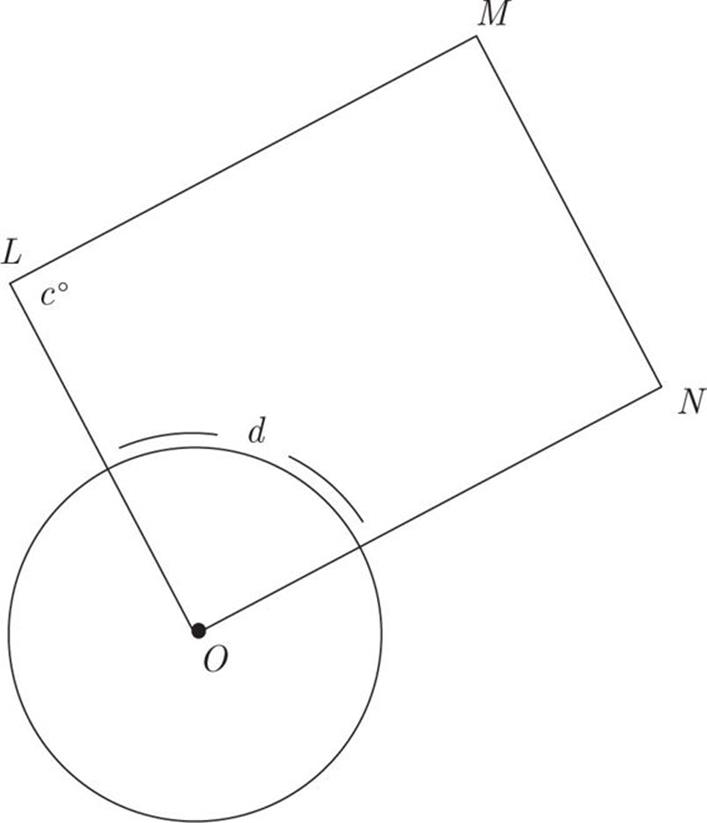
The circumference of the circle with center O shown above is 15π. LMNO is a parallelogram and ∠OLM = 108°. What is the length of the minor arc?
![]() 15π
15π
![]() 9π
9π
![]() 3π
3π
![]() 2π
2π
![]() π
π
Summary
· There may only be a handful of geometry questions on the GRE, but you’ll be expected to know a fair number of rules and formulas.
· Line and angle problems typically test your knowledge of vertical angles, parallel lines, right angles, and straight angles.
· Triangles are a popular geometry topic on the GRE. Make sure you know your triangle basics, including the total degrees of a triangle, the relationship between the angles and sides of a triangle, and the third side rule.
· Right triangle problems frequently test the Pythagorean theorem and the common Pythagorean triples 3 : 4 : 5 and 5 : 12 : 13.
· Be aware of the two special right triangles that ETS likes to torture test takers with: the 45 : 45 : 90 triangle and 30 : 60 : 90 triangle.
· Know the area formulas for triangles, rectangles, squares, and circles.
· Problems involving the coordinate plane frequently test common geometry concepts such as the area of a triangle or a square. Other plane geometry questions will test you on slope and the equation of a line.
· Slope is defined as rise over run. Find it by finding the change in y-coordinates (the rise) and the change in x-coordinates (the run).
· The equation of a line is y = mx + b, where x and y are the coordinates of any point on the line, m is the slope and b is the y-intercept, the point at which the line crosses the y-axis.
· Don’t forget to Plug In on geometry problems!