GRE Premier 2017 with 6 Practice Tests
Part III. QUANTITATIVE REASONING
Chapter 10. Math Foundations and Content Review
Arithmetic
TERMS
Consecutive numbers: Numbers of a certain type, following one another without interruption. Numbers may be consecutive in ascending or descending order. The GRE prefers to test consecutive integers (e.g., −2, −1, 0, 1, 2, 3, . . . ), but you may encounter other types of consecutive numbers. For example:
−4, −2, 0, 2, 4, 6, . . . is a series of consecutive even numbers.
−3, 0, 3, 6, 9, . . . is a series of consecutive multiples of 3.
2, 3, 5, 7, 11, . . . is a series of consecutive prime numbers.
Cube: A number raised to the 3rd power. For example 43 = (4)(4)(4) = 64, showing that 64 is the cube of 4.
Decimal: A fraction written in decimal system format. For example, 0.6 is a decimal. To convert a fraction to a decimal, divide the numerator by the denominator. For instance, ![]()
Decimal system: A numbering system based on the powers of 10. The decimal system is the only numbering system used on the GRE. Each figure, or digit, in a decimal number occupies a particular position, from which it derives its place value.
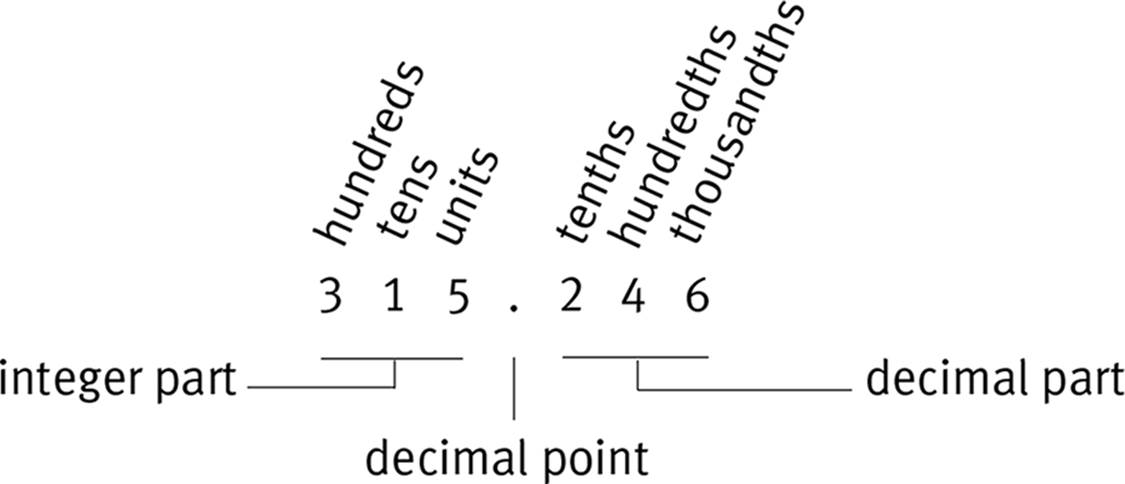
Denominator: The quantity in the bottom of a fraction, representing the whole.
Difference: The result of subtraction.
Digit: One of the numerals 0, 1, 2, 3, 4, 5, 6, 7, 8, or 9. A number can have several digits. For example, the number 542 has three digits: a 5, a 4, and a 2. The number 321,321,000 has nine digits but only four distinct (different) digits: 3, 2, 1, and 0.
Distinct: Different from each other. For example, 12 has three prime factors (2, 2, and 3) but only 2 distinct factors (2 and 3).
Element: One of the members of a set.
Exponent: The number that denotes the power to which another number or variable is raised. The exponent is typically written as a superscript to a number. For example, 53 equals (5)(5)(5). The exponent is also occasionally referred to as a “power.” For example, 53 can be described as “5 to the 3rd power.” The product, 125, is “the 3rd power of 5.” Exponents may be positive or negative integers or fractions, and they may include variables.
Fraction: The division of a part by a whole. ![]() For example,
For example, ![]() is a fraction.
is a fraction.
Integer: A number without fractional or decimal parts, including positive and negative whole numbers and zero. All integers are multiples of 1. The following are examples of integers: −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5.
Number Line: A straight line, extending infinitely in either direction, on which numbers are represented as points. The number line below shows the integers from −3 to 4. Decimals and fractions can also be depicted on a number line, as can irrational numbers, such as ![]()
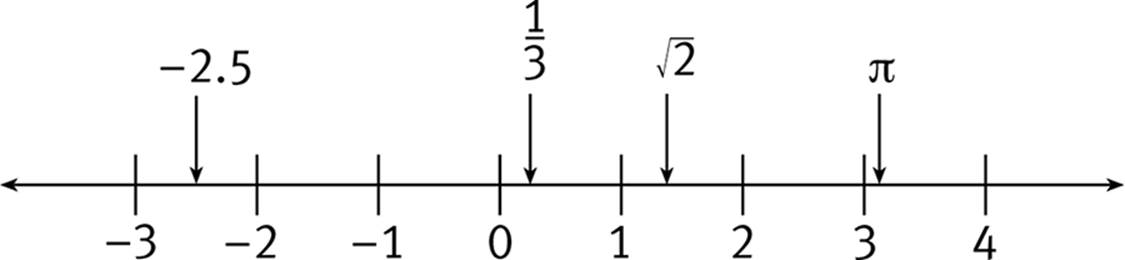
The values of numbers get larger as you move to the right along the number line. Numbers to the right of zero are positive; numbers to the left of zero are negative. Zero is neither positive nor negative. Any positive number is larger than any negative number. For example, −300 < 4.
Numerator: The quantity in the top of a fraction, representing the part.
Operation: A function or process performed on one or more numbers. The four basic arithmetic operations are addition, subtraction, multiplication, and division.
Part: A specified number of the equal sections that compose a whole.
Product: The result of multiplication.
Sequence: Lists that have an infinite number of terms, in order. The terms of a sequence are often indicated by a letter with a subscript indicating the position of the number in the sequence. For instance, a3 denotes the third number in a sequence, while an indicates the nth term in a sequence.
Set: A well-defined collection of items, typically numbers, objects, or events. The bracket symbols { } are normally used to define sets of numbers. For example, {2, 4, 6, 8} is a set of numbers.
Square: The product of a number multiplied by itself. A squared number has been raised to the 2nd power. For example, 42 = (4)(4) = 16, and 16 is the square of 4.
Sum: The result of addition.
Whole: A quantity that is regarded as a complete unit.
SYMBOLS
1. =is equal to
2. ≠is not equal to
3. 4. >is greater than 5. ≤is less than or equal to 6. ≥is greater than or equal to 7. ÷divided by 8. πpi (the ratio of the circumference of a circle to the diameter) 9. ±plus or minus 10. 11.∠angle RULES OF OPERATION There are certain mathematical laws governing the results of the four basic operations: addition, subtraction, multiplication, and division. Although you won’t need to know the names of these laws for the GRE, you’ll benefit from understanding them. PEMDAS A string of operations must be performed in proper order. The acronym PEMDAS stands for the correct order of operations: If you have trouble remembering PEMDAS, you can think of the mnemonic “Please Excuse My Dear Aunt Sally.” Example: 66 (3 − 2) ÷ 11 If you were to perform all the operations sequentially from left to right, without using PEMDAS, you would arrive at an answer of Example: Commutative Laws of Addition and Multiplication Addition and multiplication are both commutative, which means that switching the order of any two numbers being added or multiplied together does not affect the result. Example: Division and subtraction are not commutative; switching the order of the numbers changes the result. For instance, 3 − 2 ≠ 2 − 3; the left side yields a difference of 1, while the right side yields a difference of −1. Similarly, Associative Laws of Addition and Multiplication Addition and multiplication are also associative; regrouping the numbers does not affect the result. Example: The Distributive Law The distributive law of multiplication allows you to “distribute” a factor over numbers that are added or subtracted. You do this by multiplying that factor by each number in the group. Example: The law works for the numerator in division as well. However, when the sum or difference is in the denominator—that is, when you’re dividing by a sum or difference—no distribution is possible. Number Properties ADDING AND SUBTRACTING Numbers can be treated as though they have two parts: a positive or negative sign and a number. Numbers without any sign are understood to be positive. To add two numbers that have the same sign, add the number parts and keep the sign. For example, to add (−6) + (−3), add 6 and 3 and then attach the negative sign from the original numbers to the sum: (−6) + (−3) = −9. To add two numbers that have different signs, find the difference between the number parts and keep the sign of the number whose number part is larger. For example, to add (−7) + (+4), subtract 4 from 7 to get 3. Because 7 > 4 (the number part of −7 is greater than the number part of 4), the final sum will be negative: (−7) + (+4) = −3. Subtraction is the opposite of addition. You can rephrase any subtraction problem as an addition problem by changing the operation sign from a minus to a plus and switching the sign on the second number. For instance, 8 − 5 = 8 + (−5). There’s no real advantage to rephrasing if you are subtracting a smaller positive number from a larger positive number. But the concept comes in very handy when you are subtracting a negative number from any other number, a positive number from a negative number or a larger positive number from a smaller positive number. To subtract a negative number, rephrase as an addition problem and follow the rules for addition of signed numbers. For instance, 9 − (−10) = 9 + 10 = 19. To subtract a positive number from a negative number or from a smaller positive number, change the sign of the number that you are subtracting from positive to negative and follow the rules for addition of signed numbers. For example, (−4) − 1 = (−4) + (−1) = −5. MULTIPLICATION AND DIVISION OF POSITIVE AND NEGATIVE NUMBERS Multiplying or dividing two numbers with the same sign gives a positive result. Examples: Multiplying or dividing two numbers with different signs gives a negative result. Examples: ABSOLUTE VALUE The absolute value of a number is the value of a number without its sign. It is written as two vertical lines, one on either side of the number and its sign. Example: |−3| = |+3| = 3 The absolute value of a number can be thought of as the number’s distance from zero on the number line. Since both 3 and −3 are 3 units from 0, each has an absolute value of 3. If you are told that |x| = 5, x could equal 5 or −5. PROPERTIES OF ZERO Adding zero to or subtracting zero from a number does not change the number. Examples: Notice, however, that subtracting a number from zero changes the number’s sign. It’s easy to see why if you rephrase the problem as an addition problem. Example: Subtract 5 from 0. 0 − 5 = −5. That’s because 0 − 5 = 0 + (−5), and according to the rules for addition with signed numbers, 0 + (−5) = −5. The product of zero and any number is zero. Examples: Division by zero is undefined. For GRE purposes, that translates to “It can’t be done.” Since fractions are essentially division (that is, PROPERTIES OF 1 AND −1 Multiplying or dividing a number by 1 does not change the number. Examples: Multiplying or dividing a nonzero number by −1 changes the sign of the number. Examples: FACTORS, MULTIPLES, AND REMAINDERS Multiples and Divisibility A multiple is the product of a specified number and an integer. For example, 3, 12, and 90 are all multiples of 3: 3 = (3)(1); 12 = (3)(4); and 90 = (3)(30). The number 4 is not a multiple of 3, because there is no integer that can be multiplied by 3 and yield 4. Multiples do not have to be of integers, but all multiples must be the product of a specific number and an integer. For instance, 2.4, 12, and 132 are all multiples of 1.2: 2.4 = (1.2)(2); 12 = (1.2)(10); and 132 = (1.2)(110). The concepts of multiples and factors are tied together by the idea of divisibility. A number is said to be evenly divisible by another number if the result of the division is an integer with no remainder. A number that is evenly divisible by a second number is also a multiple of the second number. For example, 52 ÷ 4 = 13, which is an integer. So 52 is evenly divisible by 4, and it’s also a multiple of 4. On some GRE math problems, you will find yourself trying to assess whether one number is evenly divisible by another. You can use several simple rules to save time. · An integer is divisible by 2 if its last digit is divisible by 2. · An integer is divisible by 3 if its digits add up to a multiple of 3. · An integer is divisible by 4 if its last two digits are a multiple of 4. · An integer is divisible by 5 if its last digit is 0 or 5. · An integer is divisible by 6 if it is divisible by both 2 and 3. · An integer is divisible by 9 if its digits add up to a multiple of 9. Example: 6,930 is a multiple of 2, since 0 is even. . . . a multiple of 3, since 6 + 9 + 3 + 0 = 18, which is a multiple of 3. . . . not a multiple of 4, since 30 is not a multiple of 4. . . . a multiple of 5, since it ends in zero. . . . a multiple of 6, since it is a multiple of both 2 and 3. . . . a multiple of 9, since 6 + 9 + 3 + 0 = 18, which is a multiple of 9. Properties of Odd/Even Numbers Even numbers are integers that are evenly divisible by 2; odd numbers are integers that are not evenly divisible by 2. Integers whose last digit is 0, 2, 4, 6, or 8 are even; integers whose last digit is 1, 3, 5, 7, or 9 are odd. The terms odd and even apply only to integers, but they may be used for either positive or negative integers. 0 is considered even. Rules for Odds and Evens Note that multiplying any even number by any integer always produces another even number. It may be easier to use the Picking Numbers strategy in problems that ask you to decide whether some unknown will be odd or even. Example: Is the sum of two odd numbers odd or even? Pick any two odd numbers, for example, 3 and 5: 3 + 5 = 8. Since the sum of the two odd numbers that you picked is an even number, 8, it’s safe to say that the sum of any two odd numbers is even. Picking Numbers will work in any odds/evens problem, no matter how complicated. The only time you have to be careful is when division is involved, especially if the problem is in Quantitative Comparison format; different numbers may yield different results. Example: Integer x is evenly divisible by 2. Is By definition, any multiple of 2 is even, so integer x is even. And Factors and Primes The factors, or divisors, of an integer are the positive integers by which it is evenly divisible (leaving no remainder). Example: What are the factors of 36? 36 has nine factors: 1, 2, 3, 4, 6, 9, 12, 18, and 36. We can group these factors in pairs: (1)(36) = (2)(18) = (3)(12) = (4)(9) = (6)(6). The greatest common factor, or greatest common divisor, of a pair of integers is the largest factor that they share. Example: What is the greatest common factor of 36 and 48? To find the greatest common factor (GCF), break down both integers into their prime factorizations and multiply all the prime factors they have in common: 36 = (2)(2)(3)(3), and 48 = (2)(2)(2)(2)(3). What they have in common is two 2s and one 3, so the GCF is (2)(2)(3) = 12. A prime number is an integer greater than 1 that has only two factors: itself and 1. The number 1 is not considered a prime, because it is divisible only by itself. The number 2 is the smallest prime number and the only even prime. (Any other even number must have 2 as a factor and therefore cannot be prime.) Prime Factors The prime factorization of a number is the expression of the number as the product of its prime factors (the factors that are prime numbers). There are two common ways to determine a number’s prime factorization. The rules given above for determining divisibility by certain numbers come in handy in both methods. Method #1: Work your way up through the prime numbers, starting with 2. (You’ll save time in this process, especially when you’re starting with a large number, by knowing the first ten prime numbers by heart: 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29.) Example: What is the prime factorization of 210? 210 = (2)(105) Since 105 is odd, it can’t contain another factor of 2. The next smallest prime number is 3. The digits of 105 add up to 6, which is a multiple of 3, so 3 is a factor of 105. 210 = (2)(3)(35) The digits of 35 add up to 8, which is not a multiple of 3. But 35 ends in 5, so it is a multiple of the next largest prime number, 5. 210 = (2)(3)(5)(7) Since 7 is a prime number, this equation expresses the complete prime factorization of 210. Method #2: Figure out one pair of factors and then determine their factors, continuing the process until you’re left with only prime numbers. Those primes will be the prime factorization. Example: What is the prime factorization of 1,050? The distinct prime factors of 1,050 are therefore 2, 5, 3, and 7, with the prime number 5 occurring twice in the prime factorization. We usually write out the prime factorization by putting the prime numbers in increasing order. Here, that would be (2)(3)(5)(5)(7). The prime factorization can also be expressed in exponential form: (2)(3)(52)(7). The Least Common Multiple The least common multiple of two or more integers is the smallest number that is a multiple of each of the integers. Here’s one quick way to find it: 1. Determine the prime factorization of each integer. 2. Write out each prime number the maximum number of times that it appears in any one of the prime factorizations. 3. Multiply those prime numbers together to get the least common multiple of the original integers. Example: What is the least common multiple of 6 and 8? Start by finding the prime factors of 6 and 8. The factor 2 appears three times in the prime factorization of 8, while 3 appears as only a single factor of 6. So the least common multiple of 6 and 8 will be (2)(2)(2)(3), or 24. Note that the least common multiple of two integers is smaller than their product if they have any factors in common. For instance, the product of 6 and 8 is 48, but their least common multiple is only 24. In addition to answering questions using the term least common multiple, you’ll find the concept useful whenever you’re adding or subtracting fractions with different denominators. Remainders The remainder is what is “left over” in a division problem. A remainder is always smaller than the number you are dividing by. For instance, 17 divided by 3 is 5, with a remainder of 2. Likewise, 12 divided by 6 is 2, with a remainder of 0 (since 12 is evenly divisible by 6). GRE writers often disguise remainder problems. For instance, a problem might state that the slats of a fence are painted in three colors, which appear in a fixed order, such as red, yellow, blue, red, yellow, blue.... You would then be asked something like, “If the first slat is red, what color is the 301st slat?” Since 3 goes into 300 evenly, the whole pattern must finish on the 300th slat and start all over again on the 301st. Therefore, the 301st would be red. EXPONENTS AND ROOTS Rules of Operations with Exponents To multiply two powers with the same base, keep the base and add the exponents together. Example: 22 × 23 = (2 × 2)(2 × 2 × 2) = 25 or 22 × 23 = 22 + 3 = 25 To divide two powers with the same base, keep the base and subtract the exponent of the denominator from the exponent of the numerator. Example: or 45 ÷ 42 = 45 − 2 = 43 To raise a power to another power, multiply the exponents. Example: (32)4 = (3 × 3)4 or (32)4 = (3 × 3)(3 × 3)(3 × 3)(3 × 3) or (32)4 = 32 × 4 = 38 To multiply two powers with different bases but the same power, multiply the bases together and raise to the power. Example: (32) (52) = (3 × 3)(5 × 5) = (3 × 5)(3 × 5) = (3 × 5)2 = 152 A base with a negative exponent indicates the reciprocal of that base to the positive value of the exponent. Example: Raising any non-zero number to an exponent of zero equals 1. Examples: 50 = 1 1610 = 1 (−6)0 = 1 Commonly Tested Properties of Powers Many Quantitative Comparison problems test your understanding of what happens when negative numbers and fractions are raised to a power. Raising a fraction between zero and one to a power produces a smaller result. Example: Raising a negative number to an even power produces a positive result. Example: (−2)2 = 4 Raising a negative number to an odd power gives a negative result. Example: (−2)3 = −8 Raising an even number to any exponent gives an even number. Raising an odd number to any exponent gives an odd number. Examples: 85 = 32,768, an even number 58 = 390,625, an odd number Powers of 10 When 10 is raised to an exponent that is a positive integer, that exponent tells how many zeros the number would contain if it were written out. Example: Write 106 in ordinary notation. The exponent 6 indicates that you will need six zeros after the 1: 1,000,000. That’s because 106 means six factors of 10, that is, (10)(10)(10)(10)(10)(10). To multiply a number by a power of 10, move the decimal point the same number of places to the right as the value of the exponent (or as the number of zeros in that power of 10). Example: Multiply 0.029 by 103 The exponent is 3, so move the decimal point three places to the right. (0.029)103 = 0029. = 29 If you had been told to multiply 0.029 by 1,000, you could have counted the number of zeros in 1,000 and done exactly the same thing. Sometimes you’ll have to add zeros as placeholders. Example: Multiply 0.029 by 106. Add zeros until you can move the decimal point six places to the right: 0.029 × 106 = 0029000. = 29,000 To divide by a power of 10, move the decimal point the corresponding number of places to the left, inserting zeros as placeholders if necessary. Example: Divide 416.03 by 10,000 There are four zeros in 10,000, but only three places to the left of the decimal point. You’ll have to insert another zero: 416.03 ÷ 10,000 = .041603 = 0.041603 By convention, one zero is usually written to the left of the decimal point on the GRE. It’s a placeholder and doesn’t change the value of the number. Scientific Notation Very large numbers (and very small decimals) take up a lot of space and are difficult to work with. So, in some scientific texts, they are expressed in a shorter, more convenient form called scientific notation. For example, 123,000,000,000 would be written in scientific notation as 1.23 × 1011, and 0.000000003 would be written as 3 × 10−9. (If you’re already familiar with the concept of negative exponents, you’ll know that multiplying by 10−9 is equivalent to dividing by 109.) To express a number in scientific notation, rewrite it as a product of two factors. The first factor must be greater than or equal to 1 but less than 10. The second factor must be a power of 10. To translate a number from scientific notation to ordinary notation, use the rules for multiplying and dividing by powers of 10. Example: 5.6 × 106 = 5,600,000, or 5.6 million Rules of Operations with Roots and Radicals A square root of any non-negative number x is a number that, when multiplied by itself, yields x. Every positive number has two square roots, one positive and one negative. For instance, the positive square root of 25 is 5, because 52 = 25. The negative square root of 25 is −5, because (−5)2 also equals 25. By convention, the radical symbol When applying the four basic arithmetic operations, radicals (roots written with the radical symbol) are treated in much the same way as variables. Addition and Subtraction of Radicals Only like radicals can be added to or subtracted from one another. Example: This expression cannot be simplified any further. Multiplication and Division of Radicals To multiply or divide one radical by another, multiply or divide the numbers outside the radical signs, then the numbers inside the radical signs. Example: Example: Simplifying Radicals If the number inside the radical is a multiple of a perfect square, the expression can be simplified by factoring out the perfect square. Example: Proportions and Math Formulas FRACTIONS The simplest way to understand the meaning of a fraction is to picture the denominator as the number of equal parts into which a whole unit is divided. The numerator represents a certain number of those equal parts. On the left, the shaded portion is one of two equal parts that make up the whole. On the right, the shaded portion is three of four equal parts that make up the whole. The fraction bar is interchangeable with a division sign. You can divide the numerator of a fraction by the denominator to get an equivalent decimal. However, the numerator and denominator must each be treated as a single quantity. Example: Evaluate You can’t just rewrite the fraction as 5 + 2 ÷ 7 − 3, because the numerator and the denominator are each considered distinct quantities. Instead, you would rewrite the fraction as (5 + 2) ÷ (7 − 3). The order of operations (remember PEMDAS?) tells us that operations in parentheses must be performed first. That gives you 7 ÷ 4. Your final answer would be Equivalent Fractions Since multiplying or dividing a number by 1 does not change the number, multiplying the numerator and denominator of a fraction by the same nonzero number doesn’t change the value of the fraction—it’s the same as multiplying the entire fraction by 1. Example: Change To change the denominator from 2 to 4, you’ll have to multiply it by 2. But to keep the value of the fraction the same, you’ll also have to multiply the numerator by 2. Similarly, dividing the numerator and denominator by the same nonzero number leaves the value of the fraction unchanged. Example: Change To change the denominator from 20 to 10, you’ll have to divide it by 2. But to keep the value of the fraction the same, you’ll have to divide the numerator by the same number. Reducing (Canceling) Most fractions on the GRE are in lowest terms. That means that the numerator and denominator have no common factor greater than 1. For example, the final answer of Example: Reduce Sometimes it may be necessary to repeat the process and keep dividing out common factors until no common factor greater than 1 remains for the numerator and denominator. Example: Reduce Adding and Subtracting Fractions You cannot add or subtract fractions unless they have the same denominator. If they don’t, you’ll have to convert each fraction to an equivalent fraction with the least common denominator. Then add or subtract the numerators (not the denominators!) and, if necessary, reduce the resulting fraction to its lowest terms. Given two fractions with different denominators, the least common denominator is the least common multiple of the two denominators, that is, the smallest number that is evenly divisible by both denominators. Example: What is the least common denominator of The least common denominator of the two fractions will be the least common multiple of 15 and 10. Because 15 = (5)(3) and 10 = (5)(2), the least common multiple of the two numbers is (5)(3)(2), or 30. That makes 30 the least common denominator of Example: As we saw in the previous example, the least common denominator of the two fractions is 30. Change each fraction to an equivalent fraction with a denominator of 30. Then add: Since 13 and 30 have no common factor greater than 1, Multiplying Fractions To multiply fractions, multiply the numerators and multiply the denominators. Multiplying numerator by numerator and denominator by denominator is simple. But it’s easy to make careless errors if you have to multiply a string of fractions or work with large numbers. You can minimize those errors by reducing before you multiply. Example: Multiply First, cancel a 5 out of the 10 and the 15, a 3 out of the 3 and the 9, and a 4 out of the 8 and the 4: Then multiply numerators together and denominators together: Reciprocals To get the reciprocal of a common fraction, turn the fraction upside-down so that the numerator becomes the denominator, and vice versa. If a fraction has a numerator of 1, the fraction’s reciprocal will be equivalent to an integer. Example: What is the reciprocal of Inverting the fraction gives you the reciprocal, Since Dividing Common Fractions To divide fractions, multiply by the reciprocal of the number or fraction that follows the division sign. (The operation of division produces the same result as multiplication by the inverse.) Example: Comparing Positive Fractions Given two positive fractions with the same denominator, the fraction with the larger numerator will have the larger value. Example: Which is greater, But if you’re given two positive fractions with the same numerator but different denominators, the fraction with the smaller denominator will have the larger value. Example: Which is greater, The diagrams below show two wholes of equal size. The one on the left is divided into 4 equal parts, 3 of which are shaded. The one on the right is divided into 8 equal parts, 3 of which are shaded. If neither the numerators nor the denominators are the same, you have three options. You can turn both fractions into their decimal equivalents. Or you can express both fractions in terms of some common denominator and then see which new equivalent fraction has the largest numerator. Or you can cross multiply the numerator of each fraction by the denominator of the other. The greater result will wind up next to the greater fraction. Example: Which is greater, Since Mixed Numbers and Improper Fractions A mixed number consists of an integer and a fraction. An improper fraction is a fraction whose numerator is greater than its denominator. To convert an improper fraction to a mixed number, divide the numerator by the denominator. The number of “whole” times that the denominator goes into the numerator will be the integer portion of the improper fraction; the remainder will be the numerator of the fractional portion. Example: Convert Dividing 23 by 4 gives you 5 with a remainder of 3, so To change a mixed number to a fraction, multiply the integer portion of the mixed number by the denominator and add the numerator. This new number is your numerator. The denominator will not change. Example: Convert Properties of Fractions Between −1 and +1 The reciprocal of a fraction between 0 and 1 is greater than both the original fraction and 1. Example: The reciprocal of The reciprocal of a fraction between −1 and 0 is less than both the original fraction and −1. Example: The reciprocal of The square of a fraction between 0 and 1 is less than the original fraction. Example: But the square of any fraction between 0 and −1 is greater than the original fraction, because multiplying two negative numbers gives you a positive product and any positive number is greater than any negative number. Example: Multiplying any positive number by a fraction between 0 and 1 gives a product smaller than the original number. Example: Multiplying any negative number by a fraction between 0 and 1 gives a product greater than the original number. Example: DECIMALS Converting Decimals It’s easy to convert decimals to common fractions, and vice versa. Any decimal fraction is equivalent to some common fraction with a power of 10 in the denominator. To convert a decimal between 0 and 1 to a fraction, determine the place value of the last nonzero digit and set that value as the denominator. Then use all the digits of the decimal number as the numerator, ignoring the decimal point. Finally, if necessary, reduce the fraction to its lowest terms. Example: Convert 0.875 to a fraction in lowest terms. The last nonzero digit is the 5, which is in the thousandths place. So the denominator of the common fraction will be 1,000. The numerator will be 875: (You can ignore the zero to the left of the decimal point, since there are no nonzero digits to its left; it’s just a “placeholder.”) Both 875 and 1,000 contain a factor of 25. Canceling it out leaves you with To convert a fraction to a decimal, simply divide the numerator by the denominator. Example: What is the decimal equivalent of 4 ÷ 5 = 0.8 Comparing Decimals Knowing place values allows you to assess the relative values of decimals. Example: Which is greater, 0.254 or 0.3? Of course, 254 is greater than 3. But Here’s the simplest way to compare decimals: add zeros after the last digit to the right of the decimal point in each decimal fraction until all the decimals you’re comparing have the same number of digits. Essentially, what you’re doing is giving all the fractions the same denominator so that you can just compare their numerators. Example: Arrange in order from smallest to largest: 0.7, 0.77, 0.07, 0.707, and 0.077. The numbers 0.707 and 0.077 end at the third place to the right of the decimal point—the thousandths place. Add zeros after the last digit to the right of the decimal point in each of the other fractions until you reach the thousandths place: Therefore, 0.07 < 0.077 < 0.7 < 0.707 < 0.77. Estimation and Rounding on the GRE You should be familiar and comfortable with the practice of “rounding off” numbers. To round off a number to a particular place, look at the digit immediately to the right of that place. If the digit is 0, 1, 2, 3, or 4, don’t change the digit that is in the place to which you are rounding. If it is 5, 6, 7, 8, or 9, change the digit in the place to which you are rounding to the next higher digit. Replace all digits to the right of the place to which you are rounding with zeros. For example, to round off 235 to the tens place, look at the units place. Since it is occupied by a 5, you’ll round the 3 in the tens place up to a 4, giving you 240. If you had been rounding off 234, you would have rounded down to the existing 3 in the tens place; that would have given you 230. Example: Round off 675,978 to the hundreds place. The 7 in the tens place means that you will have to round the hundreds place up. Since there is a 9 in the hundreds place, you’ll have to change the thousands place as well. Rounding 675,978 to the hundreds place gives you 676,000. Rounding off large numbers before calculation will allow you to quickly estimate the correct answer. Estimating can save you valuable time on many GRE problems. But before you estimate, check the answer choices to see how close they are. If they are relatively close together, you’ll have to be more accurate than if they are farther apart. PERCENTS The word percent means “hundredths,” and the percent sign, %, means Percents measure a part-to-whole relationship with an assumed whole equal to 100. The percent relationship can be expressed as Like fractions, percents express the relationship between a specified part and a whole; more specifically, percents express a relationship of a part out of 100. Thus, 25%, Translating English to Math in Part-Whole Problems On the GRE, many fractions and percents appear in word problems. You’ll solve the problems by plugging the numbers you’re given into some variation of one of the three basic formulas: To avoid careless errors, look for the key words is and of. Is (or are) often introduces the part, while of almost invariably introduces the whole. Properties of 100% Since the percent sign means Example: All 1,000 registered voters in Smithtown are Democrats, Republicans, or independents. If 75% of the registered voters are Democrats and 5% are independents, how many are Republicans? We calculate that 75% + 5%, or 80% of the 1,000 registered voters, are either Democrats or independents. The three political affiliations together must account for 100% of the voters; thus, the percentage of Republicans must be 100% − 80%, or 20%. Therefore, the number of Republicans must be 20% of 1,000, which is 20% (1,000), or 200. Multiplying or dividing a number by 100% is just like multiplying or dividing by 1; it doesn’t change the value of the original number. Converting Percents To change a fraction to its percent equivalent, multiply by 100%. Example: What is the percent equivalent of To change a decimal fraction to a percent, you can use the rules for multiplying by powers of 10. Move the decimal point two places to the right and insert a percent sign. Example: What is the percent equivalent of 0.17? 0.17 = 0.17 (100%) = 17% To change a percent to its fractional equivalent, divide by 100%. Example: What is the common fraction equivalent of 32%? To convert a percent to its decimal equivalent, use the rules for dividing by powers of 10—just move the decimal point two places to the left. Example: What is the decimal equivalent of 32%? When you divide a percent by another percent, the percent sign “drops out,” just as you would cancel out a common factor. Example: Translation: There are 20 groups of 5% in 100%. But when you divide a percent by a regular number (not by another percent), the percent sign remains. Example: Translation: One-fifth of 100% is 20%. Common Percent Equivalents As you can see, changing percents to fractions, or vice versa, is pretty straightforward. But it does take a second or two that you might spend more profitably doing other computations or setting up another GRE math problem. Familiarity with the following common equivalents will save you time. Using the Percent Formula to Solve Percent Problems You can solve most percent problems by plugging the given data into the percent formula: Most percent problems give you two of the three variables and ask for the third. Example: Ben spends $30 of his annual gardening budget on seed. If his total annual gardening budget is $150, what percentage of his budget does he spend on seed? This problem specifies the whole ($150) and the part ($30) and asks for the percentage. Plugging those numbers into the percent formula gives you this: Ben spends 20% of his annual gardening budget on seed. Percent Increase and Decrease When the GRE tests percent increase or decrease, use the formula: or To find the increase or decrease, just take the difference between the original and the new. Note that the “original” is the base from which change occurs. It may or may not be the first number mentioned in the problem. Example: Two years ago, 450 seniors graduated from Inman High School. Last year, 600 seniors graduated. By what percent did the number of graduating seniors increase? The original is the figure from the earlier time (two years ago): 450. The increase is 600 − 450, or 150. So the percent increase is Example: If the price of a $120 dress is increased by 25%, what is the new selling price? To find the new whole, you’ll first have to find the amount of increase. The original whole is $120, and the percent increase is 25%. Plugging in, we find that: The amount of increase is $30, so the new selling price is $120 + $30, or $150. Multi-Step Percent Problems On some difficult problems, you’ll be asked to find more than one percent or to find a percent of a percent. Be careful: You can’t add percents of different wholes. Example: The price of an antique is reduced by 20 percent, and then this price is reduced by 10 percent. If the antique originally cost $200, what is its final price? The most common mistake in this kind of problem is to reduce the original price by a total of 20% + 10%, or 30%. That would make the final price 70 percent of the original, or 70% ($200) = $140. This is not the correct answer. In this example, the second (10%) price reduction is taken off of the first sale price—the new whole, not the original whole. To get the correct answer, first find the new whole. You can find it by calculating either $200 − (20% of $200) or 80% ($200). Either way, you will find that the first sale price is $160. That price then has to be reduced by 10%. Either calculate $160 − (10% ($160)) or 90% ($160). In either case, the final price of the antique is $144. Picking Numbers with Percents Certain types of percent problems lend themselves readily to the alternative technique of Picking Numbers. These include problems in which no actual values are mentioned, just percents. If you assign values to the percents you are working with, you’ll find the problem less abstract. You should almost always pick 100 in percent problems, because it’s relatively easy to find percentages of 100. Example: The price of a share of company A’s stock fell by 20 percent two weeks ago and by another 25 percent last week to its current price. By what percent of the current price does the share price need to rise in order to return to its original price? · 45% · 55% · · 75% · 82% Pick a value for the original price of the stock. Since this is a percent question, picking $100 will make the math easy. The first change in the price of the stock was by 20% of $100, or $20, making the new price $100 − $20 = $80. The price then fell by another 25%. You know that 25% is the same as Percent Word Problems Percent problems are often presented as word problems. We have already seen how to identify the percent, the part, and the whole in simple percent word problems. Here are some other terms that you are likely to encounter in more complicated percent word problems: Profit made on an item is the seller’s price minus the cost to the seller. If a seller buys an item for $10 and sells it for $12, he has made $2 profit. The percent of the selling price that is profit is as follows: A discount on an item is the original price minus the reduced price. If an item that usually sells for $20 is sold for $15, the discount is $5. A discount is often represented as a percentage of the original price. In this case, the The sale price is the final price after discount or decrease. Occasionally, percent problems will involve interest. Interest is given as a percent per unit of time, such as 5% per month. The sum of money invested is the principal. The most common type of interest you will see is simple interest. In simple interest, the interest payments received are kept separate from the principal. Example: If an investor invests $100 at 20% simple annual interest, how much does she have at the end of three years? The principal of $100 yields 20% interest every year. Because 20% of $100 is $20, after three years the investor will have three years of interest, or $60, plus the principal, for a total of $160. In compound interest, the money earned as interest is reinvested. The principal grows after every interest payment received. Example: If an investor invests $100 at 20% compounded annually, how much does he have at the end of 3 years? The first year the investor earns 20% of $100 = $20. So, after one year, he has $100 + $20 = $120. The second year the investor earns 20% of $120 = $24. So, after two years, he has $120 + $24 = $144. The third year the investor earns 20% of $144 = $28.80. So, after three years, he has $144 + $28.80 = $172.80. RATIOS A ratio is the proportional relationship between two quantities. The ratio, or relationship, between two numbers (for example, 2 and 3) may be expressed with a colon between the two numbers (2:3), in words (“the ratio of 2 to 3”), or as a fraction To translate a ratio in words to numbers separated by a colon, replace to with a colon. To translate a ratio in words to a fractional ratio, use whatever follows the word of as the numerator and whatever follows the word to as the denominator. For example, if we had to express the ratio of glazed doughnuts to chocolate doughnuts in a box of doughnuts that contained 5 glazed and 7 chocolate doughnuts, we would do so as Note that the fraction Treating ratios as fractions can make computation easier. Like fractions, ratios often require division. And, like fractions, ratios ultimately should be reduced to lowest terms. Example: Joe is 16 years old, and Mary is 12 years old. Express the ratio of Joe’s age to Mary’s age in lowest terms. The ratio of Joe’s age to Mary’s age is Part:Whole Ratios In a part:whole ratio, the “whole” is the entire set (for instance, all the workers in a factory), while the “part” is a certain subset of the whole (for instance, all the female workers in the factory). In GRE ratio question stems, the word fraction generally indicates a part:whole ratio. “What fraction of the workers are female?” means “What is the ratio of the number of female workers to the total number of workers?” Example: The sophomore class at Milford Academy consists of 15 boys and 20 girls. What fraction of the sophomore class is female? The following three statements are equivalent: 1. 2. Four out of every seven sophomores are female. 3. The ratio of female sophomores to total sophomores is 4:7. Ratio vs. Actual Number Ratios are usually reduced to their simplest form (that is, to lowest terms). If the ratio of men to women in a room is 5:3, you cannot necessarily infer that there are exactly five men and three women. If you knew the total number of people in the room, in addition to the male-to-female ratio, you could determine the number of men and the number of women in the room. For example, suppose you know that there are 32 people in the room. If the male-to-female ratio is 5 to 3, then the ratio of males to the total is 5:(5 + 3), which is 5:8. You can set up an equation as Example: The ratio of domestic sales revenues to foreign sales revenues of a certain product is 3:5. What fraction of the total sales revenues comes from domestic sales? At first, this question may look more complicated than the previous example. You have to convert from a part:part ratio to a part:whole ratio (the ratio of domestic sales revenues to total sales revenues). And you’re not given actual dollar figures for domestic or foreign sales. But since all sales are either foreign or domestic, “total sales revenues” must be the sum of the revenues from domestic and foreign sales. You can convert the given ratio to a part:whole ratio because the sum of the parts equals the whole. Although it’s impossible to determine dollar amounts for the domestic, foreign, or total sales revenues from the given information, the 3:5 ratio tells you that of every $8 in sales revenues, $3 comes from domestic sales and $5 from foreign sales. Therefore, the ratio of domestic sales revenues to total sales revenues is 3:8, or You can convert a part:part ratio to a part:whole ratio (or vice versa) only if there are no missing parts and no overlap among the parts—that is, if the whole is equal to the sum of the parts. Example: In a certain bag, the ratio of the number of red marbles to the number of blue marbles is 3:5. If there are only red and blue marbles in the bag, what is the ratio of the number of red marbles to the total number of marbles? In this case, you can convert a part-to-part ratio (red marbles to blue marbles) to a part-to-whole ratio (red marbles to all marbles) because you know there are only red and blue marbles in the bag. The ratio of red marbles to the total number of marbles is 3:8. Example: Of the 25 people in Fran’s apartment building, there are 9 residents who use the roof only for tanning and 8 residents who use the roof only for gardening. The roof is only used by tanners and gardeners. Quantity A Quantity B The ratio of people who use the roof to total residents 17:25 In this question, we do not know if there is any overlap between tanners and gardeners. How many, if any, residents do both activities? Since we don’t know, the relationship cannot be determined from the information given. Ratios of More Than Two Terms Most of the ratios that you’ll see on the GRE have two terms. But it is possible to set up ratios with more than two terms. These ratios express more relationships, and therefore convey more information, than do two-term ratios. However, most of the principles discussed so far with respect to two-term ratios are just as applicable to ratios of more than two terms. Example: The ratio of x to y is 5:4. The ratio of y to z is 1:2. What is the ratio of x to z? We want the y’s in the two ratios to equal each other, because then we can combine the x:y ratio and the y:z ratio to form the x:y:z ratio that we need to answer this question. To make the y’s equal, we can multiply the second ratio by 4. When we do so, we must perform the multiplication on both components of the ratio. Since a ratio is a constant proportion, it can be multiplied or divided by any number without losing its meaning, as long as the multiplication and division are applied to all the components of the ratio. In this case, we find that the new ratio for y to z is 4:8. We can combine this with the first ratio to find a new x to y to z ratio of 5:4:8. Therefore, the ratio of x to z is 5:8. RATES A rate is a special type of ratio. Instead of relating a part to the whole or to another part, a rate relates one kind of quantity to a completely different kind. When we talk about rates, we usually use the word per, as in “miles per hour,” “cost per item,” etc. Since per means “for one” or “for each,” we express the rates as ratios reduced to a denominator of 1. Speed The most commonly tested rate on the GRE is speed. This is usually expressed in miles or kilometers per hour. The relationship between speed, distance, and time is given by the formula Anytime you can find two out of the three elements in this equation, you can find the third. For example, if a car travels 300 miles in 5 hours, it has averaged Likewise, a rearranged version of the formula can be used to solve for missing speed or time. Example: How far do you drive if you travel for 5 hours at 60 miles per hour? Example: How much time does it take to drive 300 miles at 60 miles per hour? Other Rates Speed is not the only rate that appears on the GRE. For instance, you might get a word problem involving liters per minute or cost per unit. All rate problems, however, can be solved using the speed formula and its variants by conceiving of “speed” as “rate” and “distance” as “quantity.” Example: How many hours will it take to fill a 500-liter tank at a rate of 2 liters per minute? Plug the numbers into our rate formula: Now convert 250 minutes to hours: 250 minutes ÷ 60 minutes per hour = In some cases, you should use proportions to answer rate questions. Example: If 350 widgets cost $20, how much will 1,400 widgets cost at the same rate? Set up a proportion: Solving, you will find that x = 80. So, 1,400 widgets will cost $80 at that rate. Combined Rate Problems Rates can be added. Example: Nelson can mow 200 square meters of lawn per hour. John can mow 100 square meters of lawn per hour. Working simultaneously but independently, how many hours will it take Nelson and John to mow 1,800 square meters of lawn? Add Nelson’s rate to John’s rate to find the combined rate. 200 meters per hour + 100 meters per hour = 300 meters per hour. Divide the total lawn area, 1,800 square meters, by the combined rate, 300 square meters per hour, to find the number of required hours, 6. Work Problems (Given Hours per Unit of Work) The work formula can be used to find out how long it takes a number of people working together to complete a task. Let’s say we have three people. The first takes a units of time to complete the job, the second b units of time to complete the job, and the third c units of time. If the time it takes all three working together to complete the job is T, then Example: John can weed the garden in 3 hours. If Mary can weed the garden in 2 hours, how long will it take them to weed the garden at this rate, working independently? Set John’s time per unit of work as a and Mary’s time per unit of work as b. (There is no need for the variable c, since there are only two people.) Plugging in, you find that WORK FORMULA FOR TWO When there are only two people or machines in a combined work problem, we can use a simplified work formula. Here, a = the amount of time it takes person a to complete the job, and b = the amount of time it takes person b to complete the job. Example: Let’s use the same example from above: John takes 3 hours to weed the garden, and Mary takes 2 hours to weed the same garden. How long will it take them to weed the garden together? AVERAGES The average of a group of numbers is defined as the sum of the terms divided by the number of terms. This equation can be rewritten two ways: Thus, any time you have two out of the three values (average, sum of terms, number of terms), you can find the third. Example: Henry buys three items costing $2.00, $1.75, and $1.05. What is the average price (arithmetic mean) of the three items? (Don’t let the phrase arithmetic mean throw you; it’s just another term for average.) Example: June pays an average price of $14.50 for 6 articles of clothing. What is the total price of all 6 articles? Example: The total weight of the licorice sticks in a jar is 30 ounces. If the average weight of each licorice stick is 2 ounces, how many licorice sticks are there in the jar? Using the Average to Find a Missing Number If you’re given the average, the total number of terms, and all but one of the actual numbers, you can find the missing number. Example: The average annual rainfall in Boynton for 1976−1979 was 26 inches per year. Boynton received 24 inches of rain in 1976, 30 inches in 1977, and 19 inches in 1978. How many inches of rainfall did Boynton receive in 1979? You know that total rainfall equals 24 + 30 + 19 + (number of inches of rain in 1979). You know that the average rainfall was 26 inches per year. You know that there were 4 years. So, plug these numbers into any of the three expressions of the average formula to find that Sum of terms = (Average)(Number of terms): Another Way to Find a Missing Number: The Concept of “Balanced Value” Another way to find a missing number is to understand that the sum of the differences between each term and the mean of the set must equal zero. Plugging in the numbers from the previous problem, for example, we find that: It may be easier to comprehend why this is true by visualizing a balancing, or weighting, process. The combined distance of the numbers above the average from the mean must be balanced with the combined distance of the numbers below the average from the mean. Example: The average of 63, 64, 85, and x is 80. What is the value of x? Think of each value in terms of its position relative to the average, 80. 63 is 17 less than 80. 64 is 16 less than 80. 85 is 5 greater than 80. So these three terms are a total of 17 + 16 − 5, or 28, less than the average. Therefore, x must be 28 greater than the average to restore the balance at 80. So x = 28 + 80 = 108. Average of Consecutive, Evenly Spaced Numbers When consecutive numbers are evenly spaced, the average is the middle value. For example, the average of consecutive integers 6, 7, and 8 is 7. If there is an even number of evenly spaced numbers, there is no single middle value. In that case, the average is midway between (that is, the average of) the middle two values. For example, the average of 5, 10, 15, and 20 is 12.5, midway between the middle values 10 and 15. Note that not all consecutive numbers are evenly spaced. For instance, consecutive prime numbers arranged in increasing order are not evenly spaced. But you can use the handy technique of finding the middle value whenever you have consecutive integers, consecutive odd or even numbers, consecutive multiples of an integer, or any other consecutive numbers that are evenly spaced. Combining Averages When there is an equal number of terms in each set, and only when there is an equal number of terms in each set, you can average averages. For example, suppose there are two bowlers and you must find their average score per game. One has an average score per game of 100, and the other has an average score per game of 200. If both bowlers bowled the same number of games, you can average their averages to find their combined average. Suppose they both bowled 4 games. Their combined average will be equally influenced by both bowlers. Hence, their combined average will be the average of 100 and 200. You can find this quickly by remembering that the quantity above the average and the quantity below the average must be equal. Therefore, the average will be halfway between 100 and 200, which is 150. Or, we could solve using our average formula: However, if the bowler with the average score of 100 had bowled 4 games and the bowler with the 200 average had bowled 16 games, the combined average would be weighted further toward 200 than toward 100 to reflect the greater influence of the 200 bowler than the 100 bowler upon the total. This is known as a weighted average. Again, you can solve this by using the concept of a balanced average or by using the average formula. Since the bowler bowling an average score of 200 bowled Example: A teacher surprised her students with a 5 question pop quiz. 10% of the students answered no questions correctly, 20% had 2 right answers, 30% answered 3 questions correctly, 30% had 4 right answers and 10% had a perfect score. What was the weighted average of the number of correct answers? Algebra ALGEBRAIC TERMS Variable: A letter or symbol representing an unknown quantity. Constant (term): A number not multiplied by any variable(s). Term: A numerical constant; also, the product of a numerical constant and one or more variables. Coefficient: The numerical constant by which one or more variables are multiplied. The coefficient of 3x2 is 3. A variable (or product of variables) without a numerical coefficient, such as z or xy3, is understood to have a coefficient of 1. Algebraic expression: An expression containing one or more variables, one or more constants, and possibly one or more operation symbols. In the case of the expression x, there is an implied coefficient of 1. An expression does not contain an equal sign. x, 3x2 + 2x, and Monomial: An algebraic expression with only one term. To multiply monomials, multiply the coefficients and the variables separately: 2a × 3a = (2 × 3)(a × a) = 6a2 . Polynomial: The general name for an algebraic expression with more than one term. An algebraic expression with two terms is called a binomial. Algebraic equation: Two algebraic expressions separated by an equal sign or one algebraic expression separated from a number by an equal sign. BASIC OPERATIONS Combining Like Terms The process of simplifying an expression by adding together or subtracting terms that have the same variable factors is called combining like terms. Example: Simplify the expression 2x − 5y − x + 7y. 2x − 5y − x + 7y = (2x − x) + (7y − 5y) = x + 2y Notice that the commutative, associative, and distributive laws that govern arithmetic operations with ordinary numbers also apply to algebraic terms and polynomials. Adding and Subtracting Polynomials To add or subtract polynomials, combine like terms. (3x2 + 5x + 7) − (x2 + 12) = (3x2 − x2) + 5x + (7 − 12) = 2x2 + 5x − 5 Factoring Algebraic Expressions Factoring a polynomial means expressing it as a product of two or more simpler expressions. Common factors can be factored out by using the distributive law. Example: Factor the expression 2a + 6ac. The greatest common factor of 2a + 6ac is 2a. Using the distributive law, you can factor out 2a so that the expression becomes 2a(1 + 3c). Example: All three terms in the polynomial 3x3 + 12x2 − 6x contain a factor of 3x. Pulling out the common factor yields 3x(x2 + 4x − 2). ADVANCED OPERATIONS Substitution Substitution, a process of plugging values into equations, is used to evaluate an algebraic expression or to express it in terms of other variables. Replace every variable in the expression with the number or quantity you are told is its equivalent. Then carry out the designated operations, remembering to follow the order of operations (PEMDAS). Example: Express Replace every a with 2x and every b with 3: Without more information, you can’t simplify or evaluate this expression further. Solving Equations When you manipulate any equation, always do the same thing on both sides of the equal sign. Otherwise, the two sides of the equation will no longer be equal. To solve an algebraic equation without exponents for a particular variable, you have to manipulate the equation until that variable is on one side of the equal sign with all numbers or other variables on the other side. You can perform addition, subtraction, or multiplication; you can also perform division, as long as the quantity by which you are dividing does not equal zero. Typically, at each step of the process, you’ll try to isolate the variable by using the reverse of whatever operation has been applied to the variable. For example, in solving the equation n + 6 = 10 for n, you have to get rid of the 6 that has been added to the n. You do that by subtracting 6 from both sides of the equation: n + 6 − 6 = 10 − 6, so n = 4. Example: If 4x − 7 = 2x + 5, what is the value of x? Start by adding 7 to both sides. This gives us 4x = 2x + 12. Now subtract 2x from both sides. This gives us 2x = 12. Finally, let’s divide both sides by 2. This gives us x = 6. Inequalities There are two differences between solving an inequality (such as 2x < 5) and solving an equation (such as 2x − 5 = 0). First, the solution to an inequality is almost always a range of possible values, rather than a single value. You can see the range most clearly by expressing it visually on a number line. The shaded portion of the number line above shows the set of all numbers between −4 and 0 excluding the endpoints −4 and 0; this range would be expressed algebraically by the inequality −4 < x < 0. The shaded portion of the number line above shows the set of all numbers greater than −1, up to and including 3; this range would be expressed algebraically by the inequality −1 < x ≤ 3. The other difference when solving an inequality—and the only thing you really have to remember—is that if you multiply or divide the inequality by a negative number, you have to reverse the direction of the inequality. For example, when you multiply both sides of the inequality −3x < 2 by −1, you get 3x > −2. Example: Solve for x: Multiply both sides of the inequality by 4: 12 − x ≥ 8 Subtract 12 from both sides: −x ≥ −4 Multiply (or divide) both sides by −1 and change the direction of the inequality sign: x ≤ 4 As you can see from the number line, the range of values that satisfies this inequality includes 4 and all numbers less than 4. Solving for One Unknown in Terms of Another In general, in order to solve for the value of an unknown, you need as many distinct equations as you have variables. If there are two variables, for instance, you need two distinct equations. However, some GRE problems do not require you to solve for the numerical value of an unknown. Instead, you are asked to solve for one variable in terms of the other(s). To do so, isolate the desired variable on one side of the equation and move all the constants and other variables to the other side. Example: In the formula Clear the denominator by multiplying both sides by a + yb: (a + yb)z = xy Remove parentheses by distributing: az + ybz = xy Put all terms containing y on one side and all other terms on the other side: az = xy − ybz Factor out the common factor, y: az = y(x − bz) Divide by the coefficient of y to get y alone: Simultaneous Equations We’ve already discovered that you need as many different equations as you have variables to solve for the actual value of a variable. When a single equation contains more than one variable, you can only solve for one variable in terms of the others. This has important implications for Quantitative Comparisons. To have enough information to compare the two quantities, you usually must have at least as many equations as you have variables. On the GRE, you will often have to solve two simultaneous equations, that is, equations that give you different information about the same two variables. There are two methods for solving simultaneous equations. Method 1—Substitution Step 1: Solve one equation for one variable in terms of the second. Step 2: Substitute the result back into the other equation and solve. Example: If x − 15 = 2y and 6y + 2x = −10, what is the value of y? Solve the first equation for x by adding 15 to both sides. x = 2y + 15 Substitute 2y + 15 for x in the second equation: Method 2—Adding to Cancel Combine the equations in such a way that one of the variables cancels out. To solve the two equations 4x + 3y = 8 and x + y = 3, multiply both sides of the second equation by −3 to get −3x − 3y = −9. Now add the two equations; the 3y and the −3y cancel out, leaving: x = −1. Before you use either method, make sure you really do have two distinct equations. For example, 2x + 3y = 8 and 4x + 6y = 16 are really the same equation in different forms; multiply the first equation by 2, and you’ll get the second. Whichever method you use, you can check the result by plugging both values back into both equations and making sure they fit. Example: If m = 4n − 10 and 3m + 2n = 26, find the values of m and n. Since the first equation already expresses m in terms of n, this problem is best approached by substitution. Substitute 4n − 10 for m into 3m + 2n = 26, and solve for n. Now solve either equation for m by plugging in 4 for n. m = 4n − 10 m = 4(4) − 10 m = 16 − 10 m = 6 So m = 6 and n = 4. Example: If 3x + 3y = 18 and x − y = 10, find the values of x and y. You could solve this problem by the substitution method. But look what happens if you multiply the second equation by 3 and add it to the first: If 6x = 48, then x = 8. Now you can just plug 8 into either equation in place of x and solve for y. Your calculations will be simpler if you use the second equation: 8 − y = 10; −y = 2; y = −2. Example: The GRE will sometimes reward you with a shortcut to finding combined value using multiple variables. If 5x + 5y = 20, what is the value of x + y? We don’t need the value of either variable by itself, but their sum. If we divided both sides by 5, we could find the value of x + y. Example: If 3x − 5y = 10 and 6y − 2x = 20, what is the value of x + y? By aligning the two equations with the same-variable order, you can see a shortcut to adding the two together to find the solution. While we don't know the individual values for x or y, we don't need to know them. Symbolism Don’t panic if you see strange symbols like ★, ✧, and ♦ in a GRE problem. Problems of this type usually require nothing more than substitution. Read the question stem carefully for a definition of the symbols and for any examples of how to use them. Then, just follow the given model, substituting the numbers that are in the question stem. Example: An operation symbolized by ✬ is defined by the equation x ✬ The ✬ symbol is defined as a two-stage operation performed on two quantities, which are symbolized in the equation as x and y. The two steps are (1) find the reciprocal of the second quantity and (2) subtract the reciprocal from the first quantity. To find the value of 2 ✬ 7, substitute the numbers 2 and 7 into the equation, replacing the x (the first quantity given in the equation) with the 2 (the first number given) and the y (the second quantity given in the equation) with the 7 (the second number given). The reciprocal of 7 is When a symbolism problem involves only one quantity, the operations are usually a little more complicated. Nonetheless, you can follow the same steps to find the correct answer. Example: Let x★ be defined by the equation: Every once in a while, you’ll see a symbolism problem that doesn’t even include an equation. The definitions in this type of problem usually test your understanding of number properties. Example: ✾x is defined as the largest even number that is less than the negative square root of x. What is the value of ✾81? · −82 · −80 · −10 · −8 · 8 Plug in 81 for x and work backward logically. The negative square root of 81 is −9 because (−9)(−9) = 81. The largest even number that is less than −9 is −10. (The number part of −8 is smaller than the number part of −9; however, you’re dealing with negative numbers, so you have to look for the even number that would be just to the left of −9 along the number line.) Thus, the correct answer choice is (C) −10. Sequences Sequences are lists of numbers. The value of a number in a sequence is related to its position in the list. Sequences are often represented on the GRE as follows: s1, s2, s3, … sn, … The subscript part of each number gives you the position of each element in the series. s1 is the first number in the list, s2 is the second number in the list, and so on. You will be given a formula that defines each element. For example, if you are told that sn = 2n + 1, then the sequence would be (2 × 1) + 1, (2 × 2) + 1, (2 × 3) + 1, … , or 3, 5, 7,… POLYNOMIALS AND QUADRATICS The FOIL Method When two binomials are multiplied, each term is multiplied by each term in the other binomial. This process is often called the FOIL method, because it involves adding the products of the First, Outer, Inner, and Last terms. Using the FOIL method to multiply out (x + 5)(x − 2), the product of the first terms is x2, the product of the outer terms is −2x, the product of the inner terms is 5x, and the product of the last terms is −10. Adding, the answer is x2 + 3x − 10. Factoring the Product of Binomials Many of the polynomials that you’ll see on the GRE can be factored into a product of two binomials by using the FOIL method backward. Example: Factor the polynomial x2 − 3x + 2. You can factor this into two binomials, each containing an x term. Start by writing down what you know: x2 − 3x + 2 = (x )(x ) You’ll need to fill in the missing term in each binomial factor. The product of the two missing terms will be the last term in the original polynomial: 2. The sum of the two missing terms will be the coefficient of the second term of the polynomial: −3. Find the factors of 2 that add up to −3. Since (−1) + (−2) = −3, you can fill the empty spaces with −1 and −2. Thus, x2 − 3x + 2 = (x − 1)(x − 2). Note: Whenever you factor a polynomial, you can check your answer by using FOIL to multiply the factors and obtain the original polynomial. Factoring the Difference of Two Squares A common factorable expression on the GRE is the difference of two squares (for example, a2 − b2). Once you recognize a polynomial as the difference of two squares, you’ll be able to factor it automatically, since any polynomial of the form a2 − b2 can be factored into a product of the form (a + b)(a − b). Example: Factor the expression 9x2 − 1. 9x2 = (3x)2 and 1 = 12, so 9x2 − 1 is the difference of two squares. Therefore, 9x2 − 1 = (3x + 1)(3x − 1). Factoring Polynomials of the Form a2 + 2ab + b2 or a2 − 2ab + b2 Any polynomial of this form is the square of a binomial expression, as you can see by using the FOIL method to multiply (a + b)(a + b) or (a − b)(a − b). To factor a polynomial of this form, check the sign in front of the 2ab term. If it’s a plus sign, the polynomial is equal to (a + b)2. If it’s a minus sign, the polynomial is equal to (a − b)2. Example: Factor the polynomial x2 + 6x + 9. x2 and 9 are both perfect squares, and 6x is 2(3x), which is twice the product of x and 3, so this polynomial is of the form a2+ 2ab + b2 with a = x and b = 3. Since there is a plus sign in front of the 6x, x2 + 6x + 9 = (a + 3)2. Quadratic Equations A quadratic equation is an equation of the form ax2 + bx + c = 0. Many quadratic equations have two solutions. In other words, the equation will be true for two different values of x. When you see a quadratic equation on the GRE, you’ll generally be able to solve it by factoring the algebraic expression, setting each of the factors equal to zero, and solving the resulting equations. Example: x2 − 3x + 2 = 0. Solve for x. To find the solutions, or roots, start by factoring x2 − 3x + 2 = 0 into (x − 2)(x − 1) = 0. The product of two quantities equals zero only if one (or both) of the quantities equals zero. So if you set each of the factors equal to zero, you will be able to solve the resulting equations for the solutions of the original quadratic equation. Setting the two binomials equal to zero gives you this: x − 2 = 0 or x − 1 = 0 That means that x can equal 2 or 1. As a check, you can plug each of those values in turn into x2 − 3x + 2 = 0, and you’ll see that either value makes the equation work. ALTERNATIVE STRATEGIES FOR MULTIPLE-CHOICE ALGEBRA Backsolving On GRE Problem Solving questions, you may find it easier to attack algebra problems by Backsolving. To Backsolve, substitute each answer choice into the equation until you find the one that satisfies the equation. Example: If x2 + 10x + 25 = 0, what is the value of x? · 25 · 10 · 5 · −5 · −10 The textbook approach to solving this problem would be to recognize the polynomial expression as the square of the binomial (x + 5) and set x + 5 = 0. That’s the fastest way to arrive at the correct answer of −5. But you could also plug each answer choice into the equation until you found the one that makes the equation true. Backsolving can be pretty quick if the correct answer is the first choice you plug in, but here, you have to get all the way down to choice (D) before you find that (−5)2 + 10(−5) + 25 = 0. Example: If · 12 · 8 · 6 · 5 · 4 To avoid having to try all five answer choices, look at the equation and decide which choice(s), if plugged in for x, would make your calculations easiest. Since x is in the numerators of the two fractions in this equation and the denominators are 3 and 6, try plugging in a choice that is divisible by both 3 and 6. Choices (A) and (C) are divisible by both numbers, so start with one of them. Choice (A): This is not true, so x cannot equal 12. Choice (C): This is correct, so x must equal 6. Therefore, choice (C) is correct. Backsolving may not be the fastest method for a multiple-choice algebra problem, but it’s useful if you don’t think you’ll be able to solve the problem in the conventional way. Picking Numbers On other types of multiple-choice algebra problems, especially where the answer choices consist of variables or algebraic expressions, you may want to Pick Numbers to make the problem less abstract. Evaluate the answer choices and the information in the question stem by picking a number and substituting it for the variable wherever the variable appears. Example: If a > 1, the ratio of 2a + 6 to a2 + 2a − 3 is · 2a · a + 3 · · · You can simplify the process by replacing the variable a with a number in each algebraic expression. Since a has to be greater than 1, why not pick 2? Then the expression 2a + 6becomes 2(2) + 6, or 10. The expression a2 + 2a − 3 becomes 22 + 2(2) − 3 = 4 + 4 − 3 = 5. So now the question reads, “The ratio of 10 to 5 is what?” That’s easy enough to answer: 10:5 is the same as If another answer choice gives you a result of 2, you will have to pick another number for a and reevaluate the expressions in the question stem and the choices that worked when you let a = 2. Choice (D) gives you Choice (E) gives you Fortunately, in this case, only choice (C) works out equal to 2, so it is the correct answer. But remember: When Picking Numbers, always check every answer choice to make sure you haven’t chosen a number that works for more than one answer choice. Using Picking Numbers to Solve for One Unknown in Terms of Another It is also possible to solve for one unknown in terms of another by Picking Numbers. If the first number you pick doesn’t lead to a single correct answer, be prepared to either pick a new number (and spend more time on the problem) or settle for guessing strategically among the answers that you haven’t eliminated. Example: If · · · · · Pick a value for x that will simplify your calculations. If you let x equal 4, then x2 − 16 = 42 − 16 = 0, and so the entire fraction on the left side of the equation is equal to zero. Now, substitute 0 for y in each answer choice in turn. Each choice is an expression for x in terms of y, and since y = 0 when x = 4, the correct answer will have to give a value of 4 when y = 0. Just remember to evaluate all the answer choices, because you might find more than one that gives a result of 4. Substituting 0 for y in choices (A), (C), and (D) yields Again, pick a number that will make calculations easy. If x = 0, then y = Therefore, y = −2 when x = 0. You don’t have to try the new value of y in all the answer choices, just in (B) and (E). When you substitute −2 for y in choice (B), you get 0. That’s what you’re looking for, but again, you have to make sure it doesn’t work in choice (E). Plugging −2 in for y in (E) yields −2 for x, so (B) is correct. TABLES, GRAPHS, AND CHARTS Some questions, especially in Data Interpretation, combine numbers and text with visual formats. Different formats are suitable for organizing different types of information. The formats that appear most frequently on GRE math questions are tables, bar graphs, line graphs, and pie charts. Questions involving tables, graphs, and charts may look different from other GRE math questions, but the ideas and principles are the same. The problems are unusual only in the way that they present information, not in what they ask you to do with that information. Tables The most basic way to organize information is to create a table. Tables are in some ways the most accurate graphic presentation format—the only way you can misunderstand a number is to read it from the wrong row or column—but they don’t allow the reader to spot trends or extremes very readily. Here’s an example of a very simple table. JOHN’S INCOME: 2007–2011 Year Income 2007 $20,000 2008 $22,000 2009 $18,000 2010 $15,000 2011 $28,000 An easy question might ask for John’s income in a particular year or for the difference in his income between two years. To find the difference, you would simply look up the amount for both years and subtract the smaller income from the larger income. A harder question might ask for John’s average annual income over the five-year period shown; to determine the average, you would have to find the sum of the five annual incomes and divide it by 5. Bar Graphs Here’s the same information that you saw previously in a table. This time, it’s presented as a bar graph. Bar graphs are somewhat less accurate than tables, but that’s not necessarily a bad attribute, especially on the GRE, where estimating often saves time on calculations. What’s handy about a bar graph is that you can see which values are larger or smaller without reading actual numbers. Just a glance at this graph shows that John’s 2011 income was almost double his 2010 income. Numbers are represented on a bar graph by the heights or lengths of the bars. For example, in the first of the two bar graphs below, the taller bar represents a value of 7. If the height or length of the bar falls between two numbers on the axis, you will have to estimate. For instance, in the second of the two bar graphs above, the shortest bar represents a value about halfway between $25 and $50, or about $37.50. Histograms Bar graphs that show relative frequencies or numbers of occurrences are called histograms. The y-axis on a histogram shows the frequency, while the x-axis might show category definitions, values, or ranges, depending on what is being graphed. These graphs can be useful in visualizing patterns and trends in the data. A quick inspection of this graph shows that the mode is 4–5 calls per minute and that the frequency distribution has a long right “tail” of occasional bursts of very high call volume. One drawback of histograms is that estimating the mean of the data can be very difficult. Segmented Bar Graphs “Regular” bar graphs only display one value for each bar. Segmented bar graphs, also called stacked bar graphs, display multiple quantities on each bar. These quantities represent different subgroups that sum to the amount at the top of each bar. Values for the first category (in this case, corn) and the total can be read directly on stacked bar charts. For instance, in 2010, the farm produced 1,500 bushels of corn and 2,400 bushels in total. Values for other categories must be calculated by subtracting the value at the bottom of the portion of the bar for that category from the value at the top of that portion of the bar. Here, wheat production is represented by the middle portion, or medium gray area, of each bar. To determine the wheat crop for 2012, find the value at the bottom of the medium gray area of the 2012 bar, 1,000, and subtract that from the value at the top of the medium gray area, 1,700. Since 1,700 − 1,000 = 700, the wheat production in 2012 was 700 bushels. Scatterplots If two measured variables are related to each other, the data are called bivariate data. A scatterplot is often the best way to graphically display such data. One variable is plotted on the x-axis, and the other is plotted on the y-axis. Thus, each ordered pair of measured values represents one data point that is plotted on the graph. Scatterplots are useful for visualizing the relationships between the two variables. A trend line shows the nature of that relationship and clearly highlights data points that deviate significantly from the general trend. The trend line can either be straight or curved, and it will frequently be drawn on the scatterplot in the question. The trend line on this scatterplot slopes upward, meaning that as the number of elementary schools in a state increases, so do the number of high schools. Notice that the scales on the axes are different; even though the apparent slope of the trend line is about 1, the number of high schools increases at a lesser rate than the number of elementary schools. Trend lines can be used to make predictions by interpolating along the trend line or extrapolating beyond the trend line. For instance, to predict the expected number of high schools for a state with 2,000 elementary schools, follow the line for 2,000 up from the x-axis until it intersects the trend line at approximately 825 to 850 high schools. Scatterplots are also useful to spot outliers, individual data points that deviate from the trend. For instance, in the scatterplot above, the data point for the state with 2,500 elementary schools and approximately 670 high schools is an outlier. Line Graphs Line graphs follow the same general principle as bar graphs, except that instead of using the lengths of bars to represent numbers, they use points connected by lines. The lines further emphasize the relative values of the numbers. To read John’s income for any particular year from this line graph, determine where a line drawn from the appropriate point would intersect the vertical axis. Pie Charts Pie charts show how things are distributed. The fraction of a circle occupied by each piece of the “pie” indicates what fraction of the whole that piece represents. In most pie charts, the percentage of the pie occupied by each “slice” will be shown on the slice itself or, for very narrow slices, outside the circle with an arrow or a line pointing to the appropriate slice. The total size of the whole pie is usually given at the top or bottom of the graph, either as “TOTAL = xxx” or as “100% = xxx.” To find the approximate amount represented by a particular piece of the pie, just multiply the whole by the appropriate percent. For instance, to find the total tax that John paid to the federal government in 2007, look at the slice of this chart labeled “Federal Taxes.” It represents 18% of John’s 2007 expenditures. Since his total 2007 expenditures were $20,000, he paid
0.18($20,000) = $3,600 in federal taxes in 2007. One important note about pie charts: If you’re not given the whole and you don’t know both the percentage and the actual number that at least one slice represents, you won’t be able to find the whole. Pie charts are ideal for presenting the kind of information that ratio problems present in words. Statistics MEDIAN, MODE, AND RANGE Median: The middle term in a group of terms that are arranged in numerical order. To find the median of a group of terms, first arrange the terms in numerical order. If there is an odd number of terms in the group, then the median is the middle term. Example: Bob’s test scores in Spanish are 84, 81, 88, 70, and 87. What is his median score? In increasing order, his scores are 70, 81, 84, 87, and 88. The median test score is the middle one: 84. If there is an even number of terms in the group, the median is the average of the two middle terms. Example: John’s test scores in biology are 92, 98, 82, 94, 85, and 97. What is his median score? In numerical order, his scores are 82, 85, 92, 94, 97, and 98. The median test score is the average of the two middle terms, or The median of a group of numbers is often different from its average. Example: Caitlin’s test scores in math are 92, 96, 90, 85, and 82. Find the difference between Caitlin’s median score and the average (arithmetic mean) of her scores. In ascending order, Caitlin’s scores are 82, 85, 90, 92, and 96. The median score is the middle one: 90. Her average score is As you can see, Caitlin’s median score and her average score are not the same. The difference between them is 90 − 89, or 1. Mode: The term that appears most frequently in a set. Example: The daily temperatures in city Q for one week were 25°, 33°, 26°, 25°, 27°, 31°, and 22°. What was the mode of the daily temperatures in city Q for that week? Each of the temperatures occurs once on the list, except for 25°, which occurs twice. Since 25° appears more frequently than any other temperature, it is the mode. A set may have more than one mode if two or more terms appear an equal number of times within the set and each appears more times than any other term. Example: The table below represents the score distribution for a class of 20 students on a recent chemistry test. Which score, or scores, are the mode? Score # of Students Receiving That Score 100 2 91 1 87 5 86 2 85 1 84 5 80 1 78 2 56 1 The largest number in the second column is 5, which occurs twice. Therefore, there were two mode scores on this test: 87 and 84. Equal numbers of students received those scores, and more students received those scores than any other score. Note that the modes are the scores that appeared most often, 84 and 87, not the number of times they appeared (5). If every element in the set occurs an equal number of times, then the set has no mode. Range: The distance between the greatest and least values in a group of data points. Find the range of a set of numbers by subtracting the smallest number in the set from the largest. Note that sets with the same mean or median may have very different ranges. For instance, while the median of both the sets {−11, −6, −1, 4, 9} and {−3, −2, −1, 0, 1} is the same (that is, −1), the numbers in the first set are much more spread out. The range of the first set is 9 − (−11) = 20, while the range of the second set is 1 − (−3) = 4. QUARTILES Not many GRE questions ask about quartiles or the interquartile range, but if you are striving for a very high score, read on. The first step in determining quartiles is to arrange the terms in your data set in numerical order. Next, subdivide the set of terms into four quarters, each containing an equal number of terms. The largest number in the first (lowest) group will represent the first quartile, which is often written as Q1. The largest number in the second group is Q2. Similarly, Q3 is the top of the third quartile, and Q4 is the maximum value in the set. Example: List the values of the first, second, third, and fourth quartiles for the following group of numbers: {0, 0, 0, 1, 1, 3, 7, 7, 8, 8, 9, 10, 11, 12, 13, 14} Since there are 16 terms in the list, each quartile will contain 4 numbers. The terms are in numerical order, so they do not need to be rearranged. The largest number in the first quartile is 1, so Q1 = 1. Every fourth number will be a quartile, so Q2 = 7, Q3 = 10, and Q4 = 14. The rules for determining quartiles if the number of terms is not evenly divisible by 4 can vary, so it is not likely that a GRE problem requiring you to determine quartiles will present a set for which the number of terms is not a multiple of 4. Interquartile Range The difference between the values of the third and first quartile values, Q3 − Q1, is the interquartile range. Because outliers fall into the bottom and top quartiles, they do not affect the interquartile range. For instance, set A: {0, 10, 10, 10, 10, 10, 10, 11, 11, 11, 11, 11} and set B: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11} both have 12 elements and a range of 11, but the data distributions within that range are very different. The first data point (the zero) in the first set is an outlier that skews the value of the range. The interquartile range of set A is 11 − 10 = 1 and that of set B is 8 − 2 = 6. This comparison shows that, with the exception of the outlier, the data in set A are more closely spaced than the data in set B. A straightforward way to visually display data dispersion by quartiles is a boxplot, also called a box-and-whisker plot. This visual depiction uses five values: L, the least number in the data; G, the greatest number; M, the median; Q1, the first quartile; and Q3, the third quartile. The interquartile range (which includes M) is drawn as a rectangular box, and straight lines extend from the sides of the box to the least and greatest values (L and G). A number line is drawn below the boxplot to show the numerical values of these points. Example: Draw a box-and-whisker plot for the set {7, 0, 3, 8, 1, 2, 7, 4, 8, 4, 5, 6, −3, 7, 3, 0} The first step is to arrange the data in ascending order: {−3, 0, 0, 1, 2, 3, 3, 4, 4, 5, 6, 7, 7, 7, 8, 8}. Next, identify the values needed for the box-and-whisker plot. L = −3 and G = 8. Since there are 16 elements in the set, Q1 = 1, Q3 = 7, and M = 4. PERCENTILES For large groups of numbers, the position of given data points is sometimes stated in percentiles rather than quartiles. The principle is the same as for quartiles, but there are 100 subdivisions instead of 4. Converting quartiles to percentiles is easy: Q1 is the same value as the 25th percentile, Q2 is the same value as the 50th percentile, Q3 is the same value as the 75th percentile, and Q4 is the same as the 100th percentile. STANDARD DEVIATION Like the range and the interquartile range, standard deviation is a way to measure how spread out the values in a given data set are. You probably won’t have to calculate the standard deviation on Test Day, but you will need to understand how it behaves, so it’s worthwhile to calculate it for a couple of lists of numbers to get a feel for it. Here’s how standard deviation is calculated: · Find the average of the data points. · Find the difference between the average and each data point. · Square each of the differences. · Find the average of the squared differences. · Take the square root of that average. Example: Calculate the standard deviation of 1, 3, 8, 11, and 12. First, find the average: Next, determine the differences between each term and 7: (1 − 7) = −6, (3 − 7) = −4, (8 − 7) = 1, (11 − 7) = 4, and (12 − 7) = 5. Square each difference and find the average of the squared differences: The standard deviation is the square root of that average: Note that the farther the data points are away from the mean, the greater the standard deviation will be. Also note that two sets whose data points are the same distance from the mean will have the same standard deviation. For example, the sets {2, 4, 6} and {8, 10, 12} will have the same standard deviation. FREQUENCY DISTRIBUTIONS A frequency distribution is a description of how often certain data values occur in a set and is typically shown in a table or histogram. As an example, take a look at the table below, which displays the frequency distribution of singing voices in a choir in two ways. The first delineates the count of singers for each vocal range; the second shows the percentage of the total choir for the different voices. Counts can be converted to percents by adding all the counts to get the total and then dividing the individual count for each category by that total to obtain the percentages. For instance, in this chart, there are 75 total singers. If 15 of them are tenors, then tenors make up Soprano 12 16% Alto 18 24% Tenor 15 20% Baritone 12 16% Bass 18 24% In a relative frequency distribution, also known as a probability distribution, the frequency with which given values occur is given in decimal form rather than as percentages. The value of a randomly chosen value from a known distribution of data is called a random variable X. The table below is an example of a probability distribution of such a variable. 5% of the values in the distribution are 0, 10% are 1, 20% are 2, and so on. Or, stated differently, the probability that a randomly selected value will be a zero is 0.05, the probability that a randomly selected value will be 1 is 0.10, the probability that a randomly selected value will be 2 is 0.20, etc. X P(X) 0 0.05 1 0.10 2 0.20 3 0.30 4 0.25 5 0.10 Note that you can calculate the mean by using a weighted average approach (discussed earlier in this chapter): 0.05(0) + 0.10(1) + 0.20(2) + 0.30(3) + 0.25(4) + 0.10(5) = 0 + 0.10 + 0.40 + 0.90 + 1.00 + 0.50 = 2.90. We mentioned above that frequency distributions can be shown as histograms. If the sample set of an experiment is large enough, as in the example below, the histogram begins to closely resemble a continuous curve. Normal Distribution There is a special kind of frequency distribution, called the normal distribution, that is closely tied to the concept of standard deviation. Many natural data sets, such as the distribution of the heights of adult males in the United States, very closely approximate the normal distribution. This distribution is commonly referred to as a bell curve because of its shape. Only two parameters are needed to define any normal distribution: the mean and the standard deviation. In a normal distribution, the mean equals the median, and the data are symmetrically distributed around the mean, so the curve to the left of the mean is a mirror image of the curve to the right. Normal curves 1 and 2 have the same mean, but curve 2 has a greater standard deviation—that is, curve 2 is much more spread out. Curve 3 has a greater mean value than either curve 1 or curve 2 but has a smaller standard deviation, so it is less spread out. The graph below shows some important probability values that hold true for all normal distributions. The percentage of the area under any portion of a distribution curve equals the probability that a randomly selected event will fall within that area’s range. Example The lengths of boards cut at a sawmill are normally distributed with a mean of 96.00 inches and a standard deviation of 0.05 inch. What is the approximate probability that a randomly selected board will be longer than 96.10 inches? A board longer than 96.10 inches would be 0.10 inches longer than the mean value. The standard deviation of the board lengths is 0.05 inches, so a 96.10 inch long board would be 2 standard deviations above the mean. Because these board lengths are normally distributed, 50% are at or below the mean, 34% are within the area between the mean and 1 standard deviation above the mean, and 13% are between 1 and 2 standard deviations above the mean. The probability that a random board would be less than or equal to 96.10 inches is approximately 50% + 34% + 13% = 97%, so the probability that a board would be longer is about 100% − 97% = 3%. Counting Methods and Probability SETS Sets are groups of values that have some common property, such as the negative odd integers greater than −10 or all positive integers that are evenly divisible by 3. The items in sets are called elements or members. If all the elements in a set can be counted, such as “the number of species of birds in North America,” that set is finite. If the elements in a set are limitless (e.g., “all positive numbers that are evenly divisible by 3”), that set is infinite. The set with no elements is called the empty set, which is represented by the symbol Ø. Logically, a set with any members is defined as nonempty. If all the elements of set A are among the elements of set B, then A is a subset of B. By definition, the empty set is a subset of all sets. An important characteristic of sets is that elements are unique—that is, they are not repeated. For instance, the set of the numbers 1, 1, 2, 2, and 3 is {1, 2, 3}. Additionally, since order does not matter in sets, {1, 2, 3} is the same set as {3, 2, 1}. Lists A list is like a finite set except that the order of the elements matters and that duplicate members can be included. So 1, 2, 3 and 3, 2, 1 are different lists and 1, 2, 3, 2 is a valid list. Because order does matter in lists, elements can be uniquely identified by their position, such as “first element” or “fifth element.” Notice that sets are usually enclosed within the curly brackets, { and }, but lists are not. Set Operations The intersection of two sets is a set that consists of all the elements that are contained in both sets. (You can think of it as the overlap between the sets.) The intersection of sets Aand B is written as A ∩ B. The union of two sets is the set of all the elements that are elements of either or both sets and is written as A ∪ B. If sets have no common elements, they are referred to as mutually exclusive, and their intersection is the empty set. Drawing Venn diagrams is a helpful way to analyze the relationship among sets. The set of all possible elements that have the characteristics of the sets represented by the circles in a Venn diagram is called a universal set and is represented by U. For instance, Ucould be the set of all species of birds in the world, A the set of species native to Europe, B those native to Asia, and C those native to Australia. In the diagram above, species from other continents are included within U but are not in any specific subset. The inclusion-exclusion principle is a basic counting principle for sets. In the Venn diagram above, the shaded area represents A ∩ B (species native to both Europe and Asia), the elements that are within the intersection of A and B. Determining the number of elements in A ∪ B is a bit trickier. Merely adding the number of elements in A plus those in B is not correct because that would count the elements that show up in both sets twice. To find the number of elements in the union of two sets, use this formula: |A ∪ B| = |A| + |B| − |A ∩ B| This formula adjusts for the double-counting of elements that are in both sets. Notice that sets A and C are mutually exclusive, so |A ∩ C| = Ø. For the diagram above, |A ∪ C| = |A| + |C|. Multiplication Principle When choices or events occur one after the other and the choices or events are independent of one another, the total number of possibilities is the product of the number of options for each. For example, if a ballot offers 3 candidate choices for Office A, 4 for Office B, and 2 for Office C, the total number of different ways that a voter could fill out the ballot is 3 × 4 × 2 = 24. Occasionally, a GRE question may require a careful analysis of the number of options for each choice. If a website calls for a 3-letter password but no two letters can be the same, the total possibilities would be 26 × 25 × 24 = 15,600 because the stipulation that no two letters be the same reduces the number of choices for the second and third letters. In situations where choices are “or” rather than “and,” as long as the two groups are mutually exclusive, add instead of multiplying. A menu has 3 choices for soup and 4 salad options; diners are permitted to select a soup or salad with their dinners. In this situation, the total number of choices available is 3 + 4 = 7. COMBINATION A combination question asks you how many unordered subgroups can be formed from a larger group. Some combination questions on the GRE can be solved without any computation just by counting or listing possible combinations. Example: Allen, Betty, and Claire must wash the dishes. They decide to work in shifts of two people. How many shifts will it take before all possible combinations have been used? It is possible, and not time-consuming, to solve this problem by writing a list. Call Allen “A,” Betty “B,” and Claire “C.” There are three (AB, AC, BC) possible combinations. The Combination Formula Some combination questions use numbers that make quick, noncomputational solving difficult. In these cases, use the combination formula Example: The 4 finalists in a spelling contest win commemorative plaques. If there are 7 entrants in the spelling contest, how many possible groups of finalists are there? Plug the numbers into the combination formula, such that n is 7 (the number in the large group) and k is 4 (the number of people in each subgroup formed). At this stage, it is helpful to reduce these terms. Since 7 factorial contains all the factors of 4 factorial, we can write 7! as (7)(6)(5)(4!) and then cancel the 4! in the numerator and denominator. We can reduce further by crossing off the 6 in the numerator and the (3)(2) in the denominator. There are 35 potential groups of spelling contest finalists. When you are asked to find potential combinations from multiple groups, multiply the potential combinations from each group. Example: How many groups can be formed consisting of 2 people from room A and 3 people from room B if there are 5 people in room A and 6 people in room B? Insert the appropriate numbers into the combination formula for each room and then multiply the results. For room A, the number of combinations of 2 in a set of 5 is as follows: Reducing this, you get Reducing this, you get Multiply these to find that there are (10)(20) = 200 possible groups consisting of 2 people from room A and 3 people from room B. Sometimes the GRE will ask you to find the number of possible subgroups when choosing one item from a set. In this case, the number of possible subgroups will always equal the number of items in the set. Example: Restaurant A has 5 appetizers, 20 main courses, and 4 desserts. If a meal consists of 1 appetizer, 1 main course, and 1 dessert, how many different meals can be ordered at restaurant A? The number of possible outcomes from each set is the number of items in the set. So there are 5 possible appetizers, 20 possible main courses, and 4 possible desserts. The number of different meals that can be ordered is (5)(20)(4) = 400. PERMUTATION Within any group of items or people, there are multiple arrangements, or permutations, possible. For instance, within a group of three items (for example: A, B, C), there are six permutations (ABC, ACB, BAC, BCA, CAB, and CBA). Permutations differ from combinations in that permutations are ordered. By definition, each combination larger than 1 has multiple permutations. On the GRE, a question asking “How many ways/arrangements/orders/schedules are possible?” generally indicates a permutation problem. To find permutations, think of each place that needs to be filled in a particular arrangement as a blank space. The first place can be filled with any of the items in the larger group. The second place can be filled with any of the items in the larger group except for the one used to fill the first place. The third place can be filled with any of the items in the group except for the two used to fill the first two places, etc. Example: In a spelling contest, the winner will receive a gold medal, the second-place finisher will receive a silver medal, the third-place finisher will receive a bronze medal, and the fourth-place finisher will receive a blue ribbon. If there are 7 entrants in the contest, how many different arrangements of award winners are there? The gold medal can be won by any of 7 people. The silver medal can be won by any of the remaining 6 people. The bronze medal can be won by any of the remaining 5 people. And the blue ribbon can be won by any of the remaining 4 people. Thus, the number of possible arrangements is (7)(6)(5)(4) = 840. PROBABILITY Probability measures the likelihood that an event will occur. Probability can be represented as a fraction, decimal, or percent. For example, if rain today is just as likely as not, then the probability of rain today can be expressed as An event may include more than one outcome. For example, rolling an even number on a 6-sided die is the event that includes only the outcomes 2, 4, and 6. Many GRE probability questions are based on random experiments with a defined number of possible outcomes, such as drawing a random card from a full deck. If all the possible outcomes of the experiment are equally likely to occur, you can use this formula to calculate probability: Example: What is the probability of tossing a fair coin four consecutive times and having the coin land heads up exactly once? Since a coin is tossed four times and each toss has two possible outcomes, the total number of outcomes, using the multiplication principle, is 2 × 2 × 2 × 2 = 24 = 16. The total number of desired outcomes can be easily counted: HTTT, THTT, TTHT, or TTTH. So there are 4 desired outcomes, and the probability of rolling exactly one head is The total of the probabilities of all possible outcomes in an experiment must equal 1. For instance, the probability of a tossed coin landing heads up is Example: What is the probability of tossing a fair coin four consecutive times and having the coin land heads up 0, 2, 3, or 4 times? In the last example, we found that the probability of the coin landing heads up exactly once is 0.25. To find the probability of the coin landing heads up not exactly once, subtract that probability from 1: 1 − 0.25 = 0.75. In many probability questions involving more than one event, the events are independent; one event does not affect the other. If the first toss of a fair coin results in a tail, the probability of the result of the second toss being a tail is still 0.5. In other cases the results are not independent. If there are 4 red disks and 4 green disks in a bag and 2 disks are withdrawn at random without replacement, the probability for the result of the second draw is dependent on the result of the first draw. If the first disk drawn is red, then only 3 red disks remain out of a total of 7, and the probability of drawing another red disk on the second draw is Probability of Multiple Events To calculate the probability of two or more independent events occurring, multiply the probabilities of the individual events. For example, the probability of rolling a 3 four consecutive times on a six-sided die would be You can also calculate the probability of two or more dependent events occurring by multiplying their individual probabilities, but you must calculate the probability of each dependent event as if the preceding event had resulted in the desired outcome or outcomes. Example: A bag contains 10 marbles, 4 of which are blue and 6 of which are red. If 2 marbles are removed without replacement, what is the probability that both marbles removed are red? The probability that the first marble removed will be red is What about the probability of one or another event occurring? On the GRE, you can interpret “the probability of A or B” to mean “the probability of A or B or both,” and the formula for calculating this is similar to the inclusion-exclusion principle for sets described earlier in this chapter: P(A or B) = P(A) + P(B) − P(A and B) Example: Events A and B are independent. P(A) is 0.60 and P(A or B) is 0.94. What is the probability that event B occurs? Use the formula above: P(A or B) = P(A) + P(B) − P(A and B). Since the events are independent, P(A and B) = P(A) × P(B). Plug in the values given in the problem: 0.60 + P(B) − (0.60 × P(B)) = 0.94, then simplify: Geometry LINES AND ANGLES A line is a one-dimensional geometrical abstraction—infinitely long, with no width. A straight line is the shortest distance between any two points. There is exactly one straight line that passes through any two points. Example: In the figure above, AC = 9, BD = 11, and AD = 15. What is the length of BC? When points are in a line and the order is known, you can add or subtract lengths. Since AC = 9 and AD = 15, CD = AD − AC = 15 − 9 = 6. Now, since BD = 11 and CD = 6, BC = BD − CD = 11 − 6 = 5. A line segment is a section of a straight line of finite length, with two endpoints. A line segment is named for its endpoints, as in segment AB. Example: In the figure above, A and B are the endpoints of the line segment AB, and M is the midpoint (AM = MB). What is the length of AB? Since AM is 6, MB is also 6, and so AB is 6 + 6, or 12. Two lines are parallel if they lie in the same plane and never intersect regardless of how far they are extended. If line ℓ1 is parallel to line ℓ2, we write ℓ1 || ℓ2. If two lines are both parallel to a third line, then they are parallel to each other as well. A vertex is the point at which two lines or line segments intersect to form an angle. Angles are measured in degrees (°). Angles may be named according to their vertices. Sometimes, especially when two or more angles share a common vertex, an angle is named according to three points: a point along one of the lines or line segments that form the angle, the vertex point, and another point along the other line or line segment. A diagram will sometimes show a letter inside the angle; this letter may also be used to name the angle. The angle shown in the diagram above could be called ∠x, ∠ABC, or ∠B. (We use a lowercase x because x is not a point.) Sum of Angles Around a Point The sum of the measures of the angles around a point is 360°. Sum of Angles Along a Straight Line The sum of the measures of the angles on one side of a straight line is 180°. Two angles are supplementary to each other if their measures sum to 180°. Perpendicularity and Right Angles Two lines are perpendicular if they intersect at a 90° angle (a right angle). If line ℓ1 is perpendicular to line ℓ2, we write ℓ1 ⊥ ℓ2. If lines ℓ1, ℓ2, and ℓ3 all lie in the same plane, and if ℓ1 ⊥ ℓ2 and ℓ2 ⊥ ℓ3, then ℓ1 || ℓ3, as shown in the diagram below. To find the shortest distance from a point to a line, draw a line segment from the point to the line such that the line segment is perpendicular to the line. Then, measure the length of that segment. Example: ∠A of triangle ABC is a right angle. Is side BC longer or shorter than side AB? This question seems very abstract, until you draw a diagram of a right triangle, labeling the vertex with the 90° angle as point A. Line segment AB has to be the shortest route between point B and side AC, since side AB is perpendicular to side AC. If AB is the shortest line segment that can join point B to side AC, BC must be longer than AB. Note: the side opposite the 90° angle, called the hypotenuse, is always the longest side of a right triangle. Two angles are complementary to each other if their measures sum to 90°. An acute angle measures less than 90°, and an obtuse angle measures between 90° and 180°. Two angles are supplementary if their measures sum to 180°. Angle Bisectors A line or line segment bisects an angle if it splits the angle into two smaller, equal angles. Line segment BD below bisects ∠ABC, and ∠ABD has the same measure as ∠DBC. The two smaller angles are each half the size of∠ABC. Adjacent and Vertical Angles Two intersecting lines form four angles. The angles that are adjacent (next) to each other are supplementary because they lie along a straight line. The two angles that are not adjacent to each other are opposite, or vertical. Opposite angles are equal in measure because each of them is supplementary to the same adjacent angle. In the diagram above, ℓ1 intersects ℓ2 to form angles a, b, c, and d. Angles a and c are opposite, as are angles b and d. So the measures of angles a and c are equal to each other, and the measures of angles b and d are equal to each other. And each angle is supplementary to each of its two adjacent angles. Angles Around Parallel Lines Intersected by a Transversal A line that intersects two parallel lines is called a transversal. Each of the parallel lines intersects the third line at the same angle. In the figure above, a = e. Since a and e are equal, and since a = d and e = h (because they are opposite angles), a = d = e = h. By similar reasoning, b = c = f = g. In short, when two (or more) parallel lines are cut by a transversal, all acute angles formed are equal, all obtuse angles formed are equal, and any acute angle formed is supplementary to any obtuse angle formed. Example: In the diagram above, line ℓ1 is parallel to line ℓ2. What is the value of x? The angle marked x° and the angle adjacent and to the left of the 70° angle on line ℓ2 are corresponding angles. Therefore, the angle marked x° must be supplementary to the 70° angle. If 70° + x° = 180°, x must equal 110. POLYGONS Important Terms Polygon: A closed figure whose sides are straight line segments. Families or classes of polygons are named according to their number of sides. A triangle has three sides, a quadrilateral has four sides, a pentagon has five sides, and a hexagon has six sides. Triangles and quadrilaterals are by far the most important polygons on the GRE; other polygons appear only occasionally. Perimeter: The distance around a polygon; the sum of the lengths of its sides. Vertex of a polygon: A point where two sides intersect (plural: vertices). Polygons are named by assigning each vertex a letter and listing them in order, as in pentagon ABCDEbelow. Diagonal of a polygon: A line segment connecting any two nonadjacent vertices. Regular polygon: A polygon with sides of equal length and interior angles of equal measure. Small slash marks can provide important information in diagrams of polygons. Sides with the same number of slash marks are equal in length, while angles with the same number of slash marks through circular arcs have the same measure. In the triangle below, for example, a = b, and angles X and Z are equal in measure. You can figure out the sum of the interior angles of a polygon by dividing the polygon into triangles. Draw diagonals from any vertex to all the nonadjacent vertices. Then, multiply the number of triangles by 180° to get the sum of the interior angles of the polygon. This works because the sum of the interior angles of any triangle is always 180°. Example: What is the sum of the interior angles of a pentagon? Draw a pentagon (a five-sided polygon) and divide it into triangles, as discussed above. No matter how you’ve drawn the pentagon, you’ll be able to form three triangles. Therefore, the sum of the interior angles of a pentagon is 3 × 180° = 540°. TRIANGLES Important Terms Triangle: A polygon with three straight sides and three interior angles. Right triangle: A triangle with one interior angle of 90° (a right angle). Hypotenuse: The longest side of a right triangle. The hypotenuse is always opposite the right angle. Isosceles triangle: A triangle with two equal sides, which are opposite two equal angles. In the figure below, the sides opposite the two 70° angles are equal, so x = 7. Legs: The two equal sides of an isosceles triangle or the two shorter sides of a right triangle (the ones forming the right angle). Note: the third, unequal side of an isosceles triangle is called the base. Equilateral triangle: A triangle whose three sides are all equal in length and whose three interior angles each measure 60°. The altitude, or height, of a triangle is the perpendicular distance from a vertex to the side opposite the vertex. The altitude may fall inside or outside the triangle, or it may coincide with one of the sides. Interior and Exterior Angles of a Triangle The sum of the interior angles of any triangle is 180°. Therefore, in the figure below, a + b + c = 180. An exterior angle of a triangle is equal to the sum of the remote interior angles. The exterior angle labeled x° is equal to the sum of the remote angles: x = 50 + 100 = 150. The three exterior angles of any triangle add up to 360°. In the figure above, p + q + r = 360. Sides and Angles The sum of the lengths of any two sides of a triangle is greater than the length of the third side. In the triangle below, b + c > a, a + b > c, and a + c > b. If the lengths of two sides of a triangle are unequal, the greater angle lies opposite the longer side, and vice versa. In the figure above, if x > y > z, then a > b > c. Since the two legs of an isosceles triangle have the same length, the two angles opposite the legs must have the same measure. In the figure below, PQ = PR, and ∠Q = ∠R. Perimeter and Area of Triangles There is no special formula for the perimeter of a triangle; it is just the sum of the lengths of the sides. Example: If b = 2a and Incidentally, this is really an isosceles triangle, since The area of a triangle is Example: In the diagram above, the base has length 4, and the altitude has length 3. What is the area of the triangle? Since the lengths of the base and altitude were not given in specific units, such as centimeters or feet, the area of the triangle is simply said to be 6 square units. The area of a right triangle is easy to find. Think of one leg as the base and the other as the height. Then the area is one-half the product of the legs, or RIGHT TRIANGLES The right angle is always the largest angle in a right triangle; therefore, the hypotenuse, which lies opposite the right angle, is always the longest side. Pythagorean Theorem The Pythagorean theorem, which holds for all right triangles and for no other triangles, states that the square of the hypotenuse is equal to the sum of the squares of the legs. The Pythagorean theorem is very useful whenever you’re given the lengths of any two sides of a right triangle; as long as you know whether the remaining side is a leg or the hypotenuse, you can find its length by using the Pythagorean theorem. Example: What is the length of the hypotenuse of a right triangle with legs of lengths 9 and 10? If the square of the hypotenuse equals 181, then the hypotenuse itself must be the square root of 181, or Pythagorean Triples Certain ratios of integers always satisfy the Pythagorean theorem. You might like to think of them as “Pythagorean triples.” One such ratio is 3, 4, and 5. A right triangle with legs of lengths 3 and 4 and a hypotenuse of length 5 is probably the most common kind of right triangle on the GRE. Whenever you see a right triangle with legs of 3 and 4, with a leg of 3 and a hypotenuse of 5, or with a leg of 4 and a hypotenuse of 5, you immediately know the length of the remaining side. In addition, any multiple of these lengths makes another Pythagorean triple; for instance, 62 + 82 = 102, so a triangle with sides of lengths 6, 8, and 10 is also a right triangle. The other triple that commonly appears on the GRE is 5, 12, and 13. Special Right Triangles There are two more special kinds of right triangles for which you won’t have to use the Pythagorean theorem to find the lengths of the sides. There are special ratios between the lengths of the sides in isosceles right triangles (45°/45°/90° right triangles) and 30°/60°/90° right triangles (right triangles with acute angles of 30° and 60°). As you can see in the first drawing above, the sides of an isosceles right triangle are in a ratio of Example: What is the length of the hypotenuse of an isosceles right triangle with legs of length 4? You can use the Pythagorean theorem to find the hypotenuse, but it’s quicker to use the special right triangle ratios. In an isosceles right triangle, the ratio of a leg to the hypotenuse is Triangles and Quantitative Comparison All Quantitative Comparison questions require you to judge whether enough information has been given to make a comparison. In geometry, making this judgment is often a matter of knowing the correct definition or formula. For triangles, keep in mind the following: · If you know two angles, you know the third. · To find the area, you need the base and the height. · In a right triangle, if you have two sides, you can find the third. And if you have two sides, you can find the area. · In isosceles right triangles and 30°/60°/90° triangles, if you know one side, you can find everything. Be careful, though! Be sure you know as much as you think you do. Example: Quantity A Quantity B Area of right triangle ABC, where 6 You may think at first that ABC must be a 3:4:5 right triangle. Not so fast! We’re given two sides, but we don’t know which sides they are. If AB is the hypotenuse, then it is a 3:4:5 triangle and the area is QUADRILATERALS A quadrilateral is a four-sided polygon. Regardless of a quadrilateral’s shape, the four interior angles sum to 360°. A parallelogram is a quadrilateral with two pairs of parallel sides. Opposite sides are equal in length; opposite angles are equal in measure; angles that are not opposite are supplementary to each other (measure of ∠A + measure of ∠D = 180° in the figure below). A rectangle is a parallelogram with four right angles. Opposite sides are equal; diagonals are equal. A square is a rectangle with equal sides. Perimeters of Quadrilaterals To find the perimeter of any polygon, you can simply add the lengths of its sides. However, the properties of rectangles and squares lead to simple formulas that may speed up your calculations. Because the opposite sides are equal, the perimeter of a rectangle is twice the sum of the length and the width: Perimeter = 2(Length + Width) The perimeter of a 5 by 2 rectangle is 2(5 + 2) = 14. The perimeter of a square is equal to the sum of the lengths of the 4 sides. Because all 4 sides are the same length, Perimeter = 4 (Side). If the length of one side of a square is 3, the perimeter is 4 × 3 = 12. Areas of Quadrilaterals Area formulas always involve multiplication, and the results are always stated in “square” units. You can see why if you look at the drawing below: The rectangle is composed of six squares, all equal in size. Let’s say that the side of a single small square is 1 unit. Then, we would say that a single square measures “1 by 1.” That translates into math as 1 × 1, or 12—in other words, “one square unit.” As you can see from the drawing, there are 6 such square units in the rectangle. That’s its area: 6 square units. But you could also find the area by multiplying the number of squares in a row by the number of squares in a column: 3 × 2, or 6. And since we’ve defined the length of the side of a square as 1 unit, that’s also equivalent to multiplying the length of a horizontal side by the length of a vertical side: again, 3 × 2 = 6. Formulas for Area To find the area of a rectangle, multiply the length by the width. Area of rectangle = ℓw Since the length and width of a square are equal, the area formula for a square just uses the length of a side: Area of square = (Side)2 = s2 If you’re working with a parallelogram, designate one side as the base. Then, draw a line segment from one of the vertices opposite the base down to the base so that it intersects the base at a right angle. That line segment will be called the height. To find the area of the parallelogram, multiply the length of the base by the length of the height: Area of parallelogram = (Base)(Height), or A = bh Remember the following: · In a parallelogram, if you know two adjacent sides, you know all of them; and if you know two adjacent angles, you know all of them. · In a rectangle, if you know two adjacent sides, you know the area. · In a square, if you’re given virtually any measurement (area, length of a side, length of a diagonal), you can figure out the other measurements. CIRCLES Important Terms Circle: The set of all points in a plane at the same distance from a certain point. This point is called the center of the circle. A circle is labeled by its center point; circle O means the circle with center point O. Diameter: A line segment that connects two points on the circle and passes through the center of the circle. AB is a diameter of circle O above. Radius: A line segment that connects the center of the circle with any point on the circle (plural: radii). The radius of a circle is one-half the length of the diameter. In circle O above, OA, OB, and OC are radii. Central angle: An angle formed by two radii. In circle O above, AOC is a central angle. COB and BOA are also central angles. (The measure of BOA happens to be 180°.) The total degree measure of a circle is 360°. Chord: A line segment that joins two points on the circle. The longest chord of a circle is its diameter. AT is a chord of circle P below. Tangent: A line that touches only one point on the circumference of a circle. A line drawn tangent to a circle is perpendicular to the radius at the point of tangency. In the diagram above, line ℓ is tangent to circle P at point T. Circumference and Arc Length The distance around a polygon is called its perimeter; the distance around a circle is called its circumference. The ratio of the circumference of any circle to its diameter is a constant, called pi (π). For GRE purposes, the value of π is usually approximated as 3.14. Since π equals the ratio of the circumference, C, to the diameter, d, we can say that The formula for the circumference of a circle is C = πd. The circumference formula can also be stated in terms of the radius, r. Since the diameter is twice the length of the radius, that is, d = 2r, then C = 2πr. An arc is a section of the circumference of a circle. Any arc can be thought of as the portion of a circle cut off by a particular central angle. For example, in circle Q, arc ABC is the portion of the circle that is cut off by central angle AQC. Since arcs are associated with central angles, they can be measured in degrees. The degree measure of an arc is equal to that of the central angle that cuts it off. So in circle Q, arc ABC and central angle AQC would have the same degree measure. An arc that is exactly half the circumference of its circle is called a semicircle. The length of an arc is the same fraction of a circle’s circumference as its degree measure is of 360° (the degree measure of a whole circle). For an arc with a central angle measuring n°: Example: What is the length of arc ABC of circle O above? C = 2πr; therefore, if r = 6, C = 2 × π × 6 = 12 π. Since AOC measures 60°, arc ABC is Area and Sector Area Formulas The area of a circle is πr2. A sector is a portion of a circle’s area that is bounded by two radii and an arc. The shaded area of circle X is sector AXB. Like arcs, sectors are associated with central angles. And the process and formula used to find the area of a sector are similar to those used to determine arc length. First, find the degree measure of the sector’s central angle and figure out what fraction that degree measure is of 360°. Then, multiply the area of the whole circle by that fraction. In a sector whose central angle measures n°: Example: In circle O above, what is the area of sector AOC? Since ∠AOC measures 60°, a 60° “slice” of the circle is COORDINATE GEOMETRY In coordinate geometry, the locations of points in a plane are indicated by ordered pairs of real numbers. Important Terms and Concepts Plane: A flat surface that extends indefinitely in any direction. x-axis and y-axis: The horizontal (x) and vertical (y) lines that intersect perpendicularly to indicate location on a coordinate plane. Each axis is a number line. Ordered pair: Two numbers or quantities separated by a comma and enclosed in parentheses. An example would be (8,7). All the ordered pairs that you’ll see in GRE coordinate geometry problems will be in the form (x,y), where the first quantity, x, tells you how far the point is to the left or right of the y-axis, and the second quantity, y, tells you how far the point is above or below the x-axis. Coordinates: The numbers that designate distance from an axis in coordinate geometry. The first number is the x-coordinate; the second is the y-coordinate. In the ordered pair (8,7), 8 is the x-coordinate and 7 is the y-coordinate. Origin: The point where the x- and y-axes intersect; its coordinates are (0,0). Plotting Points Here’s what a coordinate plane looks like: Any point in a coordinate plane can be identified by an ordered pair consisting of its x-coordinate and its y-coordinate. Every point that lies on the x-axis has a y-coordinate of 0, and every point that lies on the y-axis has an x-coordinate of 0. When you start at the origin and move: to the right ………………… x is positive to the left ………………… x is negative up ………………… y is positive down ………………… y is negative Therefore, the coordinate plane can be divided into four quadrants, as shown below. Distances on the Coordinate Plane The distance between two points is equal to the length of the straight-line segment that has those two points as endpoints. If a line segment is parallel to the x-axis, the y-coordinate of every point on the line segment will be the same. Similarly, if a line segment is parallel to the y-axis, the x-coordinate of every point on the line segment will be the same. Therefore, to find the length of a line segment parallel to one of the axes, all you have to do is find the difference between the endpoint coordinates that do change. In the diagram below, the length of AB equals x2 − x1. You can find the length of a line segment that is not parallel to one of the axes by treating the line segment as the hypotenuse of a right triangle. Simply draw in the legs of the triangle parallel to the two axes. The length of each leg will be the difference between the x- or y-coordinates of its endpoints. Once you’ve found the lengths of the legs, you can use the Pythagorean theorem to find the length of the hypotenuse (the original line segment). In the diagram below, (DE)2 = (EF)2 + (DF)2. Example: If the coordinates of point A are (3,4) and the coordinates of point B are (6,8), what is the distance between points A and B? You don’t have to draw a diagram to use the method just described, but drawing one may help you to visualize the problem. Plot points A and B and draw in line segment AB. The length of AB is the distance between the two points. Now draw a right triangle, with AB as its hypotenuse. The missing vertex will be the intersection of a line segment drawn through point A parallel to the x-axis and a line segment drawn through point B parallel to the y-axis. Label the point of intersection C. Since the x- and y-axes are perpendicular to each other, AC and BC will also be perpendicular to each other. Point C will also have the same x-coordinate as point B and the same y-coordinate as point A. That means that point C has coordinates (6,4). To use the Pythagorean theorem, you’ll need the lengths of AC and BC. The distance between points A and C is simply the difference between their x-coordinates, while the distance between points B and C is the difference between their y-coordinates. So AC = 6 − 3 = 3, and BC = 8 − 4 = 4. If you recognize these as the legs of a 3:4:5 right triangle, you’ll know immediately that the distance between points A and B must be 5. Otherwise, you’ll have to use the Pythagorean theorem to come to the same conclusion. Equations of Lines Straight lines can be described by linear equations. Commonly: y = mx + b, where m is the slope Lines that are parallel to the x-axis have a slope of zero and therefore have the equation y = b. Lines that are parallel to the y-axis have the equation x = a, where a is the x-intercept of that line. If you’re comfortable with linear equations, you’ll sometimes want to use them to find the slope of a line or the coordinates of a point on a line. However, many such questions can be answered without determining or manipulating equations. Check the answer choices to see if you can eliminate any by common sense. Example: Line r is a straight line as shown above. Which of the following points lies on line r? · (6,6) · (7,3) · (8,2) · (9,3) · (10,2) Line r intercepts the y-axis at (0,−2), so you can plug −2 in for b in the slope-intercept form of a linear equation. Line r has a rise (∆y) of 2 and a run (∆x) of 5, so its slope is The easiest way to proceed from here is to substitute the coordinates of each answer choice into the equation in place of x and y; only the coordinates that satisfy the equation can lie on the line. Choice (E) is the best answer to start with, because 10 is the only x-coordinate that will not create a fraction on the right side of the equal sign. Plugging in (10,2) for x and y in the slope-intercept equation gives you That’s true, so the correct answer choice is (E). SOLIDS Important Terms Solid: A three-dimensional figure. The dimensions are usually called length, width, and height (ℓ, w, and h) or height, width, and depth (h, w, and d). There are only two types of solids that appear with any frequency on the GRE: rectangular solids (including cubes) and cylinders. Uniform solid: A solid that could be cut into congruent cross sections (parallel “slices” of equal size and shape) along a given axis. Solids you see on the GRE will almost certainly be uniform solids. Face: The surface of a solid that lies in a particular plane. Hexagon ABCDEF is one face of the solid pictured below. Edge: A line segment that connects adjacent faces of a solid. The sides of hexagon ABCDEF are also edges of the solid pictured above. Base: The “bottom” face of a solid as oriented in any given diagram. Rectangular solid: A solid with six rectangular faces. All edges meet at right angles. Examples of rectangular solids are cereal boxes, bricks, etc. Cube: A special rectangular solid in which all edges are of equal length, e, and therefore all faces are squares. Sugar cubes and dice without rounded corners are examples of cubes. Cylinder: A uniform solid whose horizontal cross section is a circle—for example, a soup can or a pipe that is closed at both ends. A cylinder’s measurements are generally given in terms of its radius, r, and its height, h. Lateral surface of a cylinder: The “pipe” surface, as opposed to the circular “ends.” The lateral surface of a cylinder is unlike most other surfaces of solids that you’ll see on the GRE, first because it does not lie in a plane and second because it forms a closed loop. Think of it as the label around a soup can. If you could remove it from the can in one piece, you would have an open tube. If you then cut the label and unrolled it, it would form a rectangle with a length equal to the circumference of the circular base of the can and a height equal to that of the can. Formulas for Volume and Surface Area Volume of a rectangular solid = (Area of base) (Height) = (Length × Width) (Height) = lwh Surface area of a rectangular solid = Sum of areas of faces = 2lw + 2lh + 2hw Since a cube is a rectangular solid for which l = w = h, the formula for its volume can be stated in terms of any edge: · Volume of a cube = lwh = (Edge)(Edge)(Edge) = e3 · Surface area of a cube = Sum of areas of faces = 6e2 To find the volume or surface area of a cylinder, you’ll need two pieces of information: the height of the cylinder and the radius of the base. · Volume of a cylinder = (Area of base)(Height) = πr2h · Lateral surface area of a cylinder = (Circumference of base)(Height) = 2πrh · Total surface area of a cylinder = Areas of circular ends + Lateral surface area = 2πr2 + 2πrh MULTIPLE FIGURES Some GRE geometry problems involve combinations of different types of figures. Besides the basic rules and formulas that you would use on normal geometry problems, you’ll need an intuitive understanding of how various geometrical concepts relate to each other to answer these “multiple figures” questions correctly. For example, you may have to revisualize the side of a rectangle as the hypotenuse of a neighboring right triangle or as the diameter of a circumscribed circle. Keep looking for the relationships between the different figures until you find one that leads you to the answer. Area of Shaded Regions A common multiple-figures question involves a diagram of a geometrical figure that has been broken up into different, irregularly shaped areas, often with one region shaded. You’ll usually be asked to find the area of the shaded (or unshaded) portion of the diagram. Your best bet will be to take one of the following two approaches: · Break the area into smaller pieces whose separate areas you can find; add those areas together. · Find the area of the whole figure; find the area of the region(s) that you’re not looking for; subtract the latter from the former. Example: Rectangle ABCD above has an area of 72 and is composed of 8 equal squares. What is the area of the shaded region? The first thing you have to realize is that, for the 8 equal squares to form a total area of 72, each square must have an area of 72 ÷ 8, or 9. Since the area of a square equals the square of the length of a side, each side of a square in the diagram must have a length of At this point, you choose your approach. Either one will work: Approach 1: Break up the shaded area into right triangle DEG, rectangle EFHG, and right triangle FHC. The area of triangle DEG is Approach 2: The area of unshaded right triangle AED is Inscribed/Circumscribed Figures A polygon is inscribed in a circle if all the vertices of the polygon lie on the circle. A polygon is circumscribed about a circle if all the sides of the polygon are tangent to the circle. Square ABCD is inscribed in circle O. We can also say that circle O is circumscribed about square ABCD. Square PQRS is circumscribed about circle O. We can also say that circle O is inscribed in square PQRS. When a triangle is inscribed in a semicircle in such a way that one side of the triangle coincides with the diameter of the semicircle, the triangle is a right triangle. Example: What is the diameter of semicircle O above? AC is a diameter of semicircle O because it passes through center point O. So triangle ABC fits the description given above of a right triangle. Moreover, triangle ABC is a special 5:12:13 right triangle with a hypotenuse of 13. Therefore, the length of diameter AC is 13. Example: If the length of chord · 4 · 8 · 4π · 8π · To find the circumference, we need the radius, which is either OP or OQ in this circle. We are given the length of PQ. PQ is a chord of the circle (it connects two points on the circle), but it’s also the hypotenuse of right triangle OPQ. Do we know anything else about that triangle? Since OP and OQ are both radii of the circle, they must have the same length, so the triangle is an isosceles right triangle. Using the ratio of the lengths of sides of a 45:45:90 right triangle, with PQ as the hypotenuse, the length of each radius is 4, making the circumference 2πr or 8π, answer choice (D). Other Topics DEALING WITH WORD PROBLEMS The key to solving word problems is translation: turning English into math. Rather than having an equation set up for you, you have to decide what arithmetic or algebraic operations to perform on which numbers. For example, suppose the core of a problem involves working with the equation 3j = s − 4. In a word problem, this might be presented as “If John had three times as many macaroons as he has now, he would have four fewer macaroons than Susan would.” Your job is to translate the problem from English into math. A phrase like “three times as many as John has” can be translated as 3j; the phrase “four fewer than Susan” can be translated as “s − 4.” Many people dislike word problems. But on the GRE, the math involved is often easier than in other math problems. Once you’ve translated the language, most word problems boil down to rather simple mathematical concepts and processes—probably because the testmakers figure that the extra step of translation makes the problem difficult enough. Here’s a general approach to any word problem: 1. Read through the whole question once, without lingering over details, to get a sense of the overall problem. 2. Identify and label the variables or unknowns in a way that makes it easy to remember what they stand for. 3. Translate the problem into one or more equations, sentence by sentence. Be careful of the order in which you translate the terms. For example, consider the phrase “5 less than 4x equals 9.” The correct way to translate it is “4x − 5 = 9.” But many students make the mistake of writing the terms in the order in which they appear in words: “5 − 4x = 9.” 4. Solve the equation(s). 5. Check your work, if time permits. Translation Table This table contains common phrases used in GRE math problems. The left column lists words and phrases that occur frequently; the right column lists the corresponding algebraic symbols. equals, is, was, will be, has, costs, adds up to, is the same as = times, of, multiplied by, product of, twice, double, half, triple × divided by, per, out of, each, ratio of _ to _ ÷ plus, added to, sum, combined, and, total + minus, subtracted from, less than, decreased by, difference between − what, how much, how many, a number variable (x, n, etc.) Example: Beatrice has three dollars more than twice the number of dollars Allan has. Translate into B = 3 + 2A. For Word Problems: Add… · when you are given the amounts of individual quantities and asked to find the total. Example: If the sales tax on a $12.00 lunch is $1.20, what is the total amount of the check? $12.00 + $1.20 = $13.20 · when you are given an original amount and an increase and are then asked to find the new amount. Example: The bus fare used to be 55 cents. If the fare increased by 35 cents, what is the new fare? 55 cents + 35 cents = 90 cents Subtract… · when you are given the total and one part of the total and you want to find the remaining part or parts. Example: If 32 out of 50 children are girls, what is the number of boys? 50 children − 32 girls = 18 boys · when you are given two numbers and asked how much more or how much less one number is than the other. The amount is called the difference. Example: How much larger than 30 is 38? 38 (larger) − 30 (smaller) = 8 Multiply… · when you are given an amount for one item and asked for the total amount of many of these items. Example: If 1 book costs $6.50, what is the cost of 12 copies of the same book? 12($6.50) = $78.00 Divide… · when you are given a total amount for many items and asked for the amount for one item. Example: If 5 pounds of apples cost $6.75, what is the price of 1 pound of apples? $6.75 ÷ 5 = $1.35 · when you are given the size of one group and the total size for many such identical groups and are asked how many of the small groups fit into the larger one. Example: How many groups of 30 students can be formed from a total of 240 students? 240 ÷ 30 = 8 groups of 30 students SPECIAL WORD PROBLEMS TIP #1 Don’t try to combine several sentences into one equation; each sentence usually translates into a separate equation. SPECIAL WORD PROBLEMS TIP #2 Pay attention to what the question asks for and make a note to yourself if it is not one of the unknowns in the equation(s). Otherwise, you may stop working on the problem too early. LOGIC PROBLEMS You won’t always have to set up an equation to solve a word problem. Some of the word problems you’ll encounter on the GRE won’t fall into recognizable textbook categories. Many of these problems are designed to test your analytical and deductive logic. You can solve them with common sense and a little basic arithmetic. Ask yourself how it would be helpful to arrange the information, such as by drawing a diagram or making a table. In these problems, the issue is not so much translating English into math as simply using your head. The problem may call for nonmath skills, including the ability to organize and keep track of different possibilities, the ability to visualize something (for instance, the reverse side of a symmetrical shape), the ability to think of the exception that changes the answer to a problem, or the ability to deal with overlapping groups. Example: If ! and ∫ are digits and (!!)(∫∫) = 60∫, what is the value of ∫? Since each of the symbols represents a digit from 0–9, we know that the product of the multiplication equals a value from 600 to 609. We know that the two quantities multiplied each consist of a two-digit integer in which both digits are the same. So list the relevant two-digit integers (00, 11, 22, 33, 44, 55, 66, 77, 88, and 99) and see which two of them can be multiplied evenly into the 600 to 609 range. Only (11)(55) satisfies this requirement. The ∫ symbol equals 5.![]() square root
square root
![]() But if you perform the operation within the parentheses first, you get 66(1) ÷ 11 = 66 ÷ 11 = 6, which is the correct answer.
But if you perform the operation within the parentheses first, you get 66(1) ÷ 11 = 66 ÷ 11 = 6, which is the correct answer.
![]() the left side equals 3, while the right side equals
the left side equals 3, while the right side equals ![]()
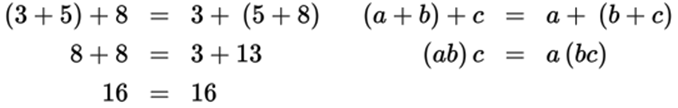
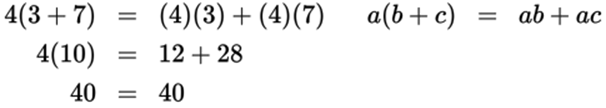
![]()
![]() is not equal to
is not equal to ![]()
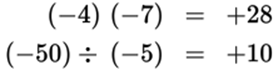
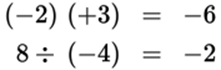
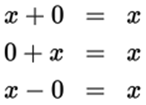
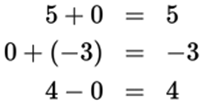
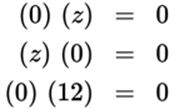
![]() means 1 ÷ 4), any fraction with zero in the denominator is also undefined. So when you are given a fraction that has an algebraic expression in the denominator, be sure that the expression cannot equal zero.
means 1 ÷ 4), any fraction with zero in the denominator is also undefined. So when you are given a fraction that has an algebraic expression in the denominator, be sure that the expression cannot equal zero.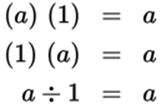
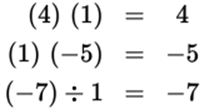
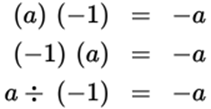
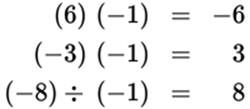
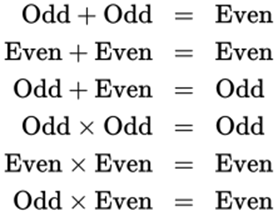
![]() even?
even?![]() must be an integer. But is
must be an integer. But is ![]() even or odd? In this case, picking two different even numbers for x can yield two different results. If you let x = 4, then
even or odd? In this case, picking two different even numbers for x can yield two different results. If you let x = 4, then ![]() which is even. But if you let x = 6, then
which is even. But if you let x = 6, then ![]() which is odd. So
which is odd. So ![]() could be even or odd—and you wouldn’t know that if you picked only one number.
could be even or odd—and you wouldn’t know that if you picked only one number.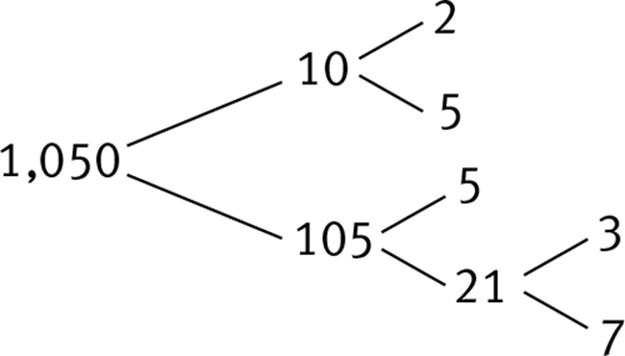

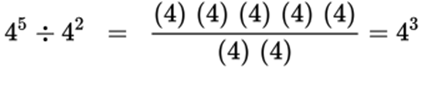
![]()
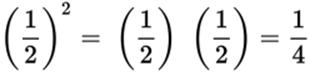
![]() stands for the positive square root only. Therefore,
stands for the positive square root only. Therefore, ![]() only, even though both 32 and (−3)2 equal 9.
only, even though both 32 and (−3)2 equal 9. 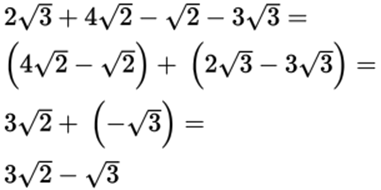
![]()
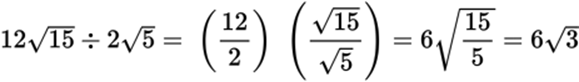
![]()

![]()
![]()
![]() or 1.75, depending on the form of the answer choices.
or 1.75, depending on the form of the answer choices.![]() into an equivalent fraction with a denominator of 4.
into an equivalent fraction with a denominator of 4.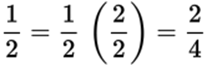
![]() into an equivalent fraction with a denominator of 10.
into an equivalent fraction with a denominator of 10.![]()
![]() that we obtained in the previous example was not in lowest terms, because both 8 and 10 are divisible by 2. In contrast, the fraction
that we obtained in the previous example was not in lowest terms, because both 8 and 10 are divisible by 2. In contrast, the fraction ![]() is in lowest terms, because there is no factor greater than 1 that 7 and 10 have in common. To convert a fraction to its lowest terms, we use a method called reducing, or canceling. To reduce, simply divide any common factors out of both the numerator and the denominator.
is in lowest terms, because there is no factor greater than 1 that 7 and 10 have in common. To convert a fraction to its lowest terms, we use a method called reducing, or canceling. To reduce, simply divide any common factors out of both the numerator and the denominator.![]() to lowest terms.
to lowest terms.![]() (because a 5 cancels out, top and bottom)
(because a 5 cancels out, top and bottom)![]() to lowest terms.
to lowest terms.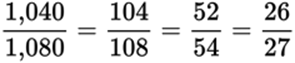
![]() and
and ![]()
![]() and
and ![]()
![]()
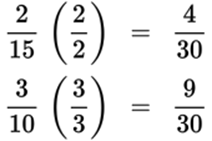
![]()
![]() is in lowest terms. You can’t reduce it further.
is in lowest terms. You can’t reduce it further.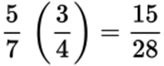
![]()

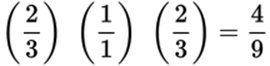
![]()
![]() But dividing a number by 1 doesn’t change the value of the number.
But dividing a number by 1 doesn’t change the value of the number.![]() the reciprocal of
the reciprocal of ![]() equals 25.
equals 25.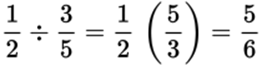
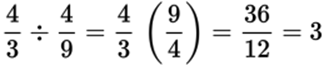
![]() or
or ![]()
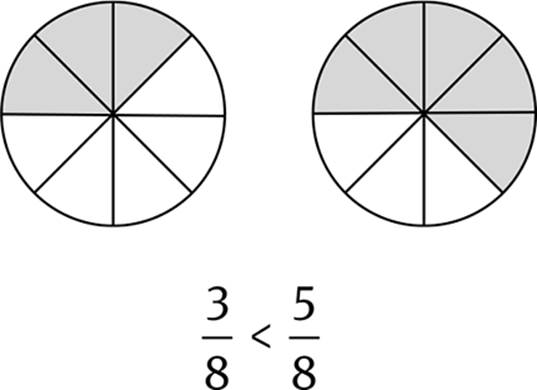
![]() or
or ![]()
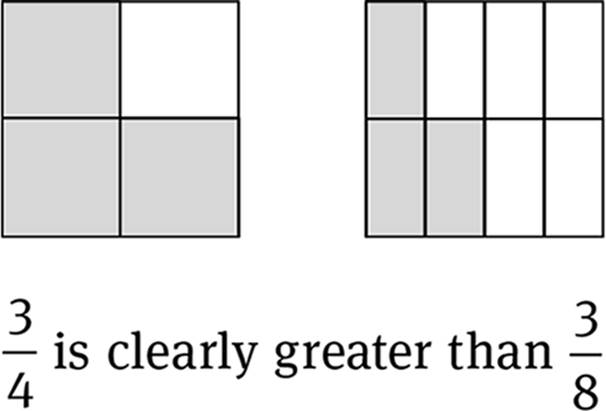
![]() or
or ![]()
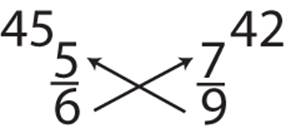
![]()
![]() to a mixed number.
to a mixed number.![]()
![]() to a fraction.
to a fraction.![]()
![]() is
is ![]() which is greater than both 1 and
which is greater than both 1 and ![]()
![]() is
is ![]() or
or ![]() which is less than both −1 and
which is less than both −1 and ![]()
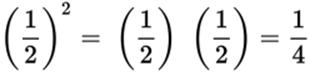
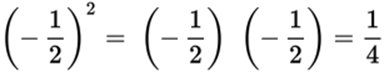
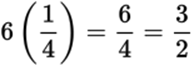
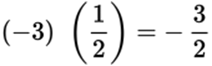
![]()
![]() Reducing that further by a factor of 5 gives you
Reducing that further by a factor of 5 gives you ![]() which is in lowest terms.
which is in lowest terms.![]()
![]() which is equivalent to
which is equivalent to ![]() while 0.254 is equivalent to only
while 0.254 is equivalent to only ![]() Since
Since ![]() 0.3 is greater than 0.254.
0.3 is greater than 0.254.
![]() For example, 25% means
For example, 25% means ![]() (Like the division sign, the percent sign evolved from the fractional relationship; the slanted bar in a percent sign represents a fraction bar.)
(Like the division sign, the percent sign evolved from the fractional relationship; the slanted bar in a percent sign represents a fraction bar.)![]() For example, if
For example, if ![]() of a rectangle is shaded, the percent of the rectangle that is shaded is
of a rectangle is shaded, the percent of the rectangle that is shaded is ![]()
![]() and 0.25 are simply different names for the same part-whole relationship.
and 0.25 are simply different names for the same part-whole relationship.
![]() 100% means
100% means ![]() or one whole. The key to solving some GRE percent problems is to recognize that all the parts add up to one whole: 100%.
or one whole. The key to solving some GRE percent problems is to recognize that all the parts add up to one whole: 100%.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]() and
and ![]() of $80 is $20. Therefore, the current price is $80 − $20 = $60. To return to its original price, the stock needs to rise from $60 to $100, that is, by $100 − $60 = $40. Then $40 is what percent of the current price, $60?
of $80 is $20. Therefore, the current price is $80 − $20 = $60. To return to its original price, the stock needs to rise from $60 to $100, that is, by $100 − $60 = $40. Then $40 is what percent of the current price, $60?![]()
![]()
![]()
![]()
![]()
![]() does not mean that
does not mean that ![]() of all the doughnuts are glazed doughnuts. There are 5 + 7, or 12 doughnuts altogether, so of the doughnuts,
of all the doughnuts are glazed doughnuts. There are 5 + 7, or 12 doughnuts altogether, so of the doughnuts, ![]() are glazed. The
are glazed. The ![]() ratio merely indicates the proportion of glazed to chocolate doughnuts. For every five glazed doughnuts, there are seven chocolate doughnuts.
ratio merely indicates the proportion of glazed to chocolate doughnuts. For every five glazed doughnuts, there are seven chocolate doughnuts.![]() or 4:3.
or 4:3.![]() of the sophomores are female.
of the sophomores are female.![]() Solving, you will find that the number of males in the room is 20.
Solving, you will find that the number of males in the room is 20.![]()
![]() which can be rewritten two ways:
which can be rewritten two ways: ![]() and Distance = (Speed)(Time).
and Distance = (Speed)(Time).![]() (Note that speeds are usually expressed as averages because they are not necessarily constant. In this example, the car moved at an “average speed” of 60 miles per hour, but probably not at a constant speed of 60 miles per hour.)
(Note that speeds are usually expressed as averages because they are not necessarily constant. In this example, the car moved at an “average speed” of 60 miles per hour, but probably not at a constant speed of 60 miles per hour.)


![]() hours to fill the tank. (As you can see from this problem, GRE Problem Solving questions test your ability to convert minutes into hours and vice versa. Pay close attention to what units the answer choice must use.)
hours to fill the tank. (As you can see from this problem, GRE Problem Solving questions test your ability to convert minutes into hours and vice versa. Pay close attention to what units the answer choice must use.)![]()
![]()
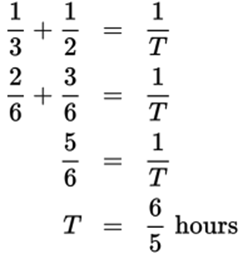
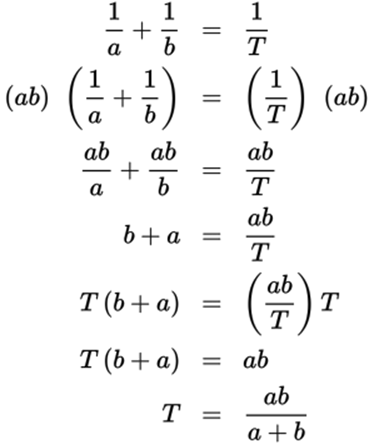
![]()
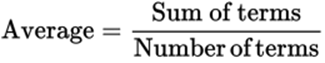


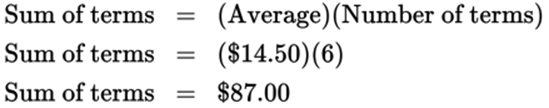
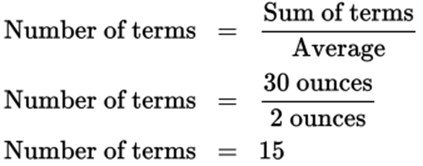

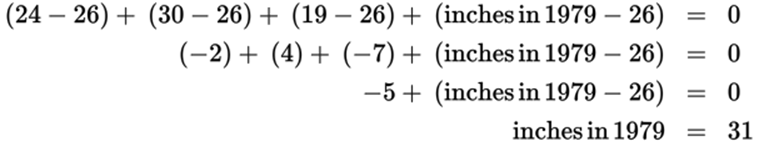
![]()
![]() of the games, the combined average will be
of the games, the combined average will be ![]() of the distance along the number line between 100 and 200, which is 180. Or, you can plug numbers into an average formula to find the following:
of the distance along the number line between 100 and 200, which is 180. Or, you can plug numbers into an average formula to find the following: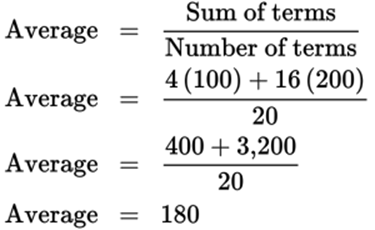
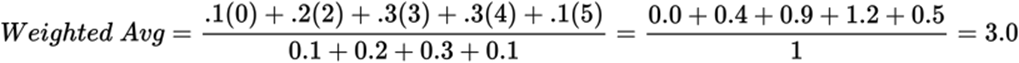
![]() are all algebraic expressions.
are all algebraic expressions.![]() in terms of x if a = 2x and b = 3.
in terms of x if a = 2x and b = 3.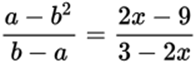

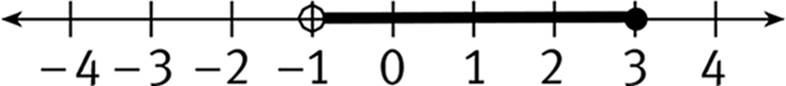
![]()
![]() solve for y in terms of x, z, a, and b.
solve for y in terms of x, z, a, and b.![]()
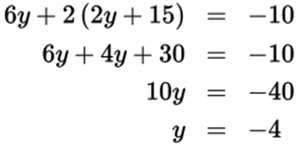
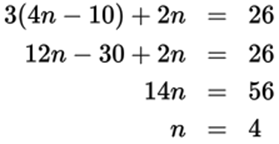
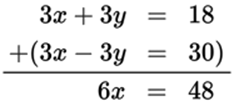
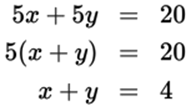
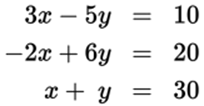
![]() What is the value of 2 ✬ 7?
What is the value of 2 ✬ 7?![]() and subtracting
and subtracting ![]() from 2 gives you the following:
from 2 gives you the following:![]()
![]() Evaluate
Evaluate ![]()
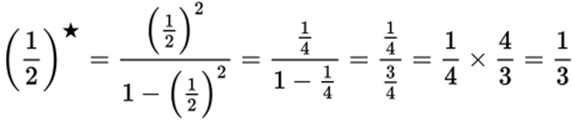
![]() x =
x =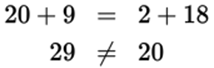
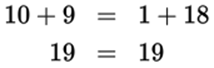
![]()
![]()
![]()
![]() or 2. Now you can just eliminate any answer choice that doesn’t give a result of 2 when you substitute 2 for a. Choice (A) gives you 2(2), or 4, so discard it. Choice (B) results in 5—also not what you want. Choice (C) yields
or 2. Now you can just eliminate any answer choice that doesn’t give a result of 2 when you substitute 2 for a. Choice (A) gives you 2(2), or 4, so discard it. Choice (B) results in 5—also not what you want. Choice (C) yields ![]() or 2. That looks good, but you can’t stop here.
or 2. That looks good, but you can’t stop here.![]() or
or ![]() so eliminate choice (D).
so eliminate choice (D).![]() or
or ![]() so discard choice (E).
so discard choice (E).![]() and x > −2, which of the following is an expression for x in terms of y?
and x > −2, which of the following is an expression for x in terms of y?![]()
![]()
![]()
![]()
![]()
![]()
![]() and
and ![]() respectively, so none of those choices can be right. But both (B) and (E) give results of 4 when you make the substitution; choosing between them will require picking another number.
respectively, so none of those choices can be right. But both (B) and (E) give results of 4 when you make the substitution; choosing between them will require picking another number.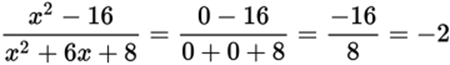
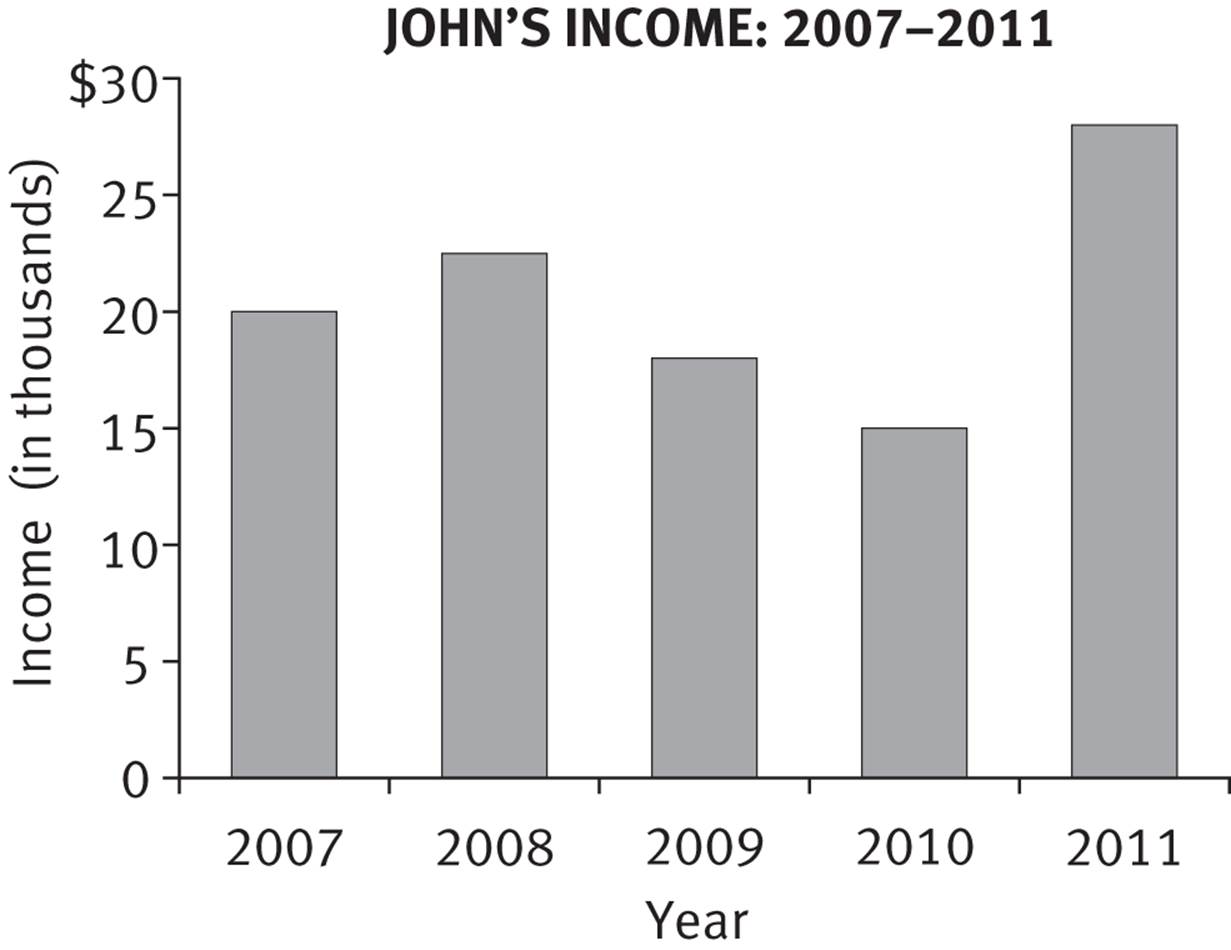
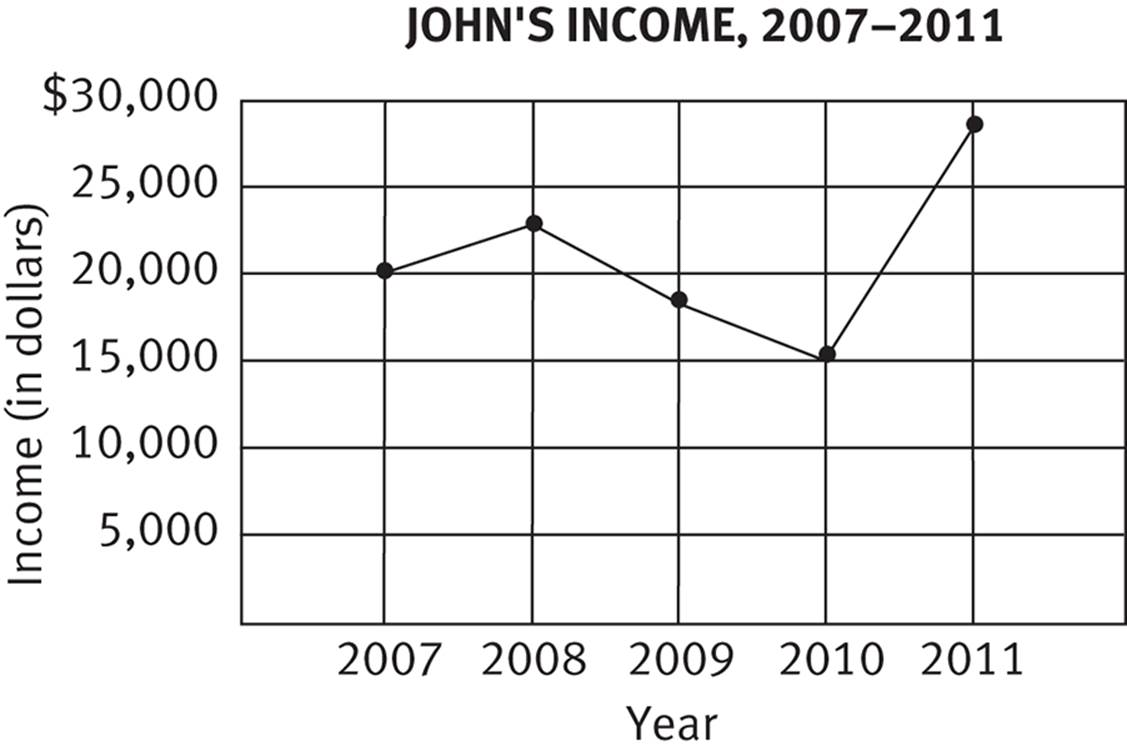
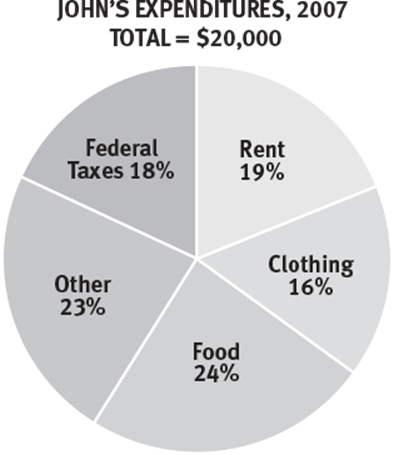
![]()
![]()
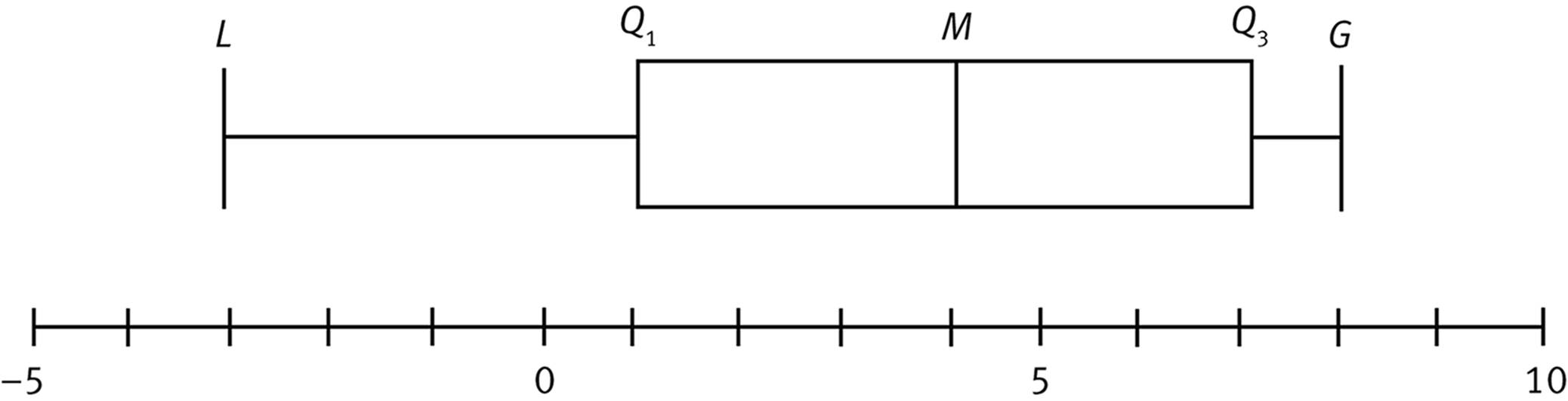
![]()
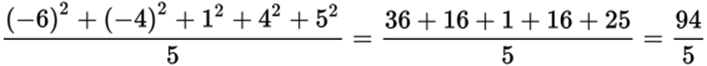
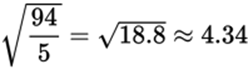
![]() of the singers.
of the singers.
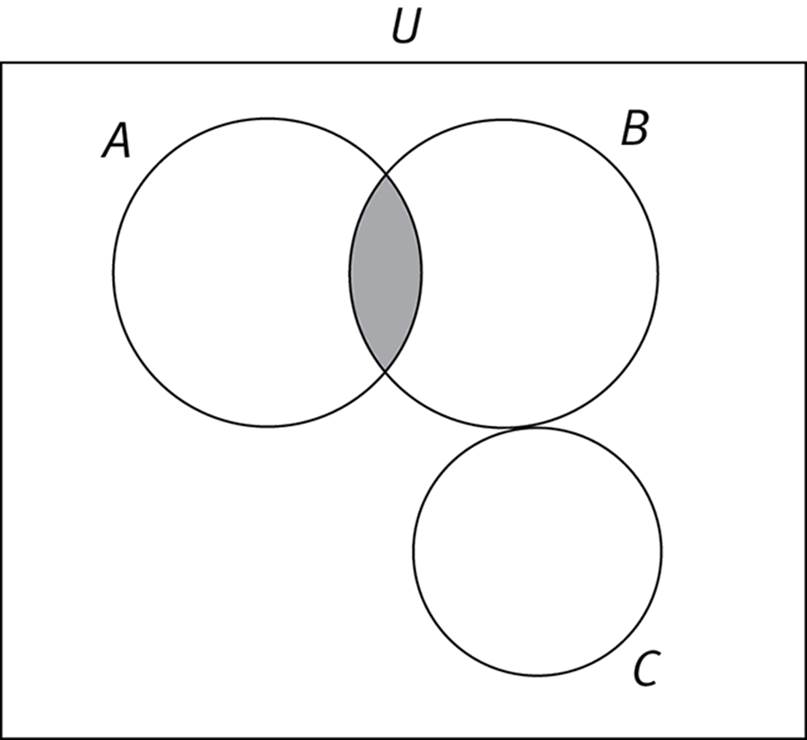
![]() where n is the number of items in the group as a whole and k is the number of items in each subgroup formed. The ! symbol means factorial (for example, 5! = (5)(4)(3)(2)(1) = 120).
where n is the number of items in the group as a whole and k is the number of items in each subgroup formed. The ! symbol means factorial (for example, 5! = (5)(4)(3)(2)(1) = 120).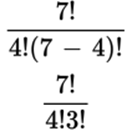
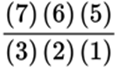
![]()
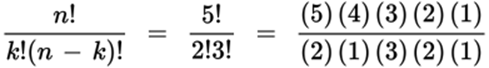
![]() For room B, the number of combinations of 3 in a set of 6 is as follows:
For room B, the number of combinations of 3 in a set of 6 is as follows: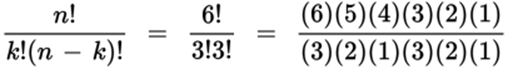
![]()
![]() 0.5, or 50%. You may also see a probability expressed in everyday language: “one chance in a hundred” means the probability is
0.5, or 50%. You may also see a probability expressed in everyday language: “one chance in a hundred” means the probability is![]() Every probability is expressed as a number between 0 and 1 inclusive, with a probability of 0 meaning “no chance” and a probability of 1 meaning “guaranteed to happen.” The higher the probability, the greater the chance that an event will occur.
Every probability is expressed as a number between 0 and 1 inclusive, with a probability of 0 meaning “no chance” and a probability of 1 meaning “guaranteed to happen.” The higher the probability, the greater the chance that an event will occur.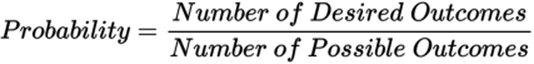
![]()
![]() The probability of the coin landing tails up is also
The probability of the coin landing tails up is also ![]() There are no other possible outcomes, and
There are no other possible outcomes, and ![]() By this same logic, if P(E) is the probability that an event will occur, then 1 − P(E) is the probability that the event will not occur. This is a useful fact in many probability questions.
By this same logic, if P(E) is the probability that an event will occur, then 1 − P(E) is the probability that the event will not occur. This is a useful fact in many probability questions.![]() If, however, the first draw is green, then 4 of the remaining 7 disks are red, and the probability of drawing red on the second draw is
If, however, the first draw is green, then 4 of the remaining 7 disks are red, and the probability of drawing red on the second draw is ![]()

![]() The probability that the second marble removed will be red will not be the same, however. There will be fewer marbles overall, so the denominator will be one less. There will also be one fewer red marble. (Note that since we are asking about the odds of picking two red marbles, we are only interested in choosing a second marble if the first was red. Don’t concern yourself with situations in which a blue marble is chosen first.) If the first marble removed is red, the probability that the second marble removed will also be red is
The probability that the second marble removed will be red will not be the same, however. There will be fewer marbles overall, so the denominator will be one less. There will also be one fewer red marble. (Note that since we are asking about the odds of picking two red marbles, we are only interested in choosing a second marble if the first was red. Don’t concern yourself with situations in which a blue marble is chosen first.) If the first marble removed is red, the probability that the second marble removed will also be red is ![]() So the probability that both marbles removed will be red is
So the probability that both marbles removed will be red is 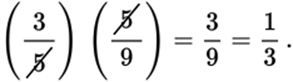
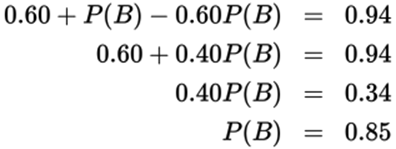

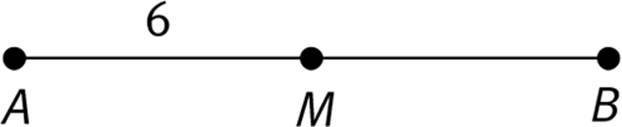
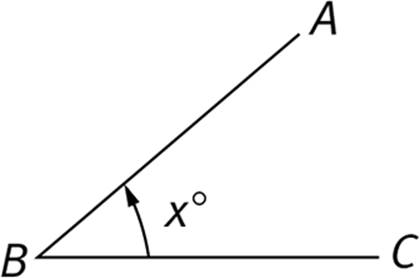
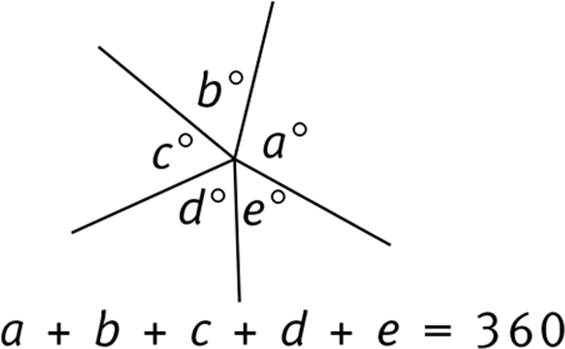

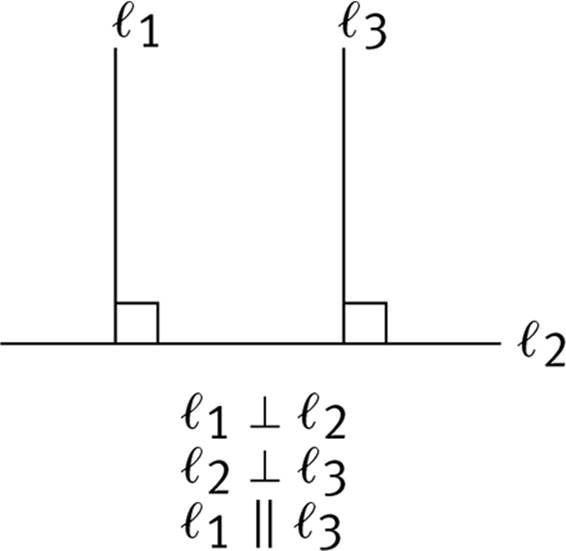
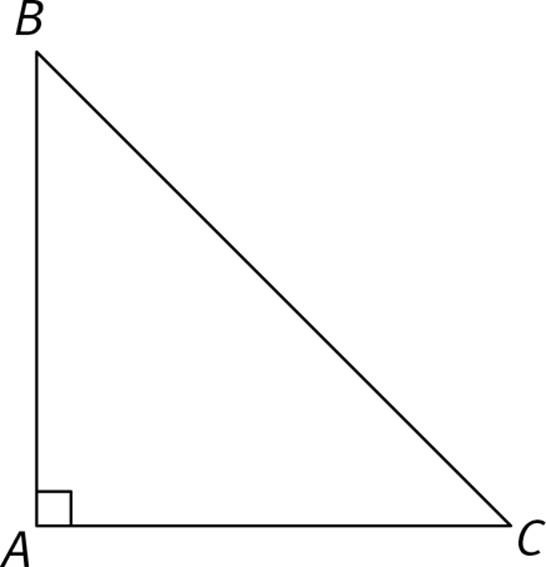
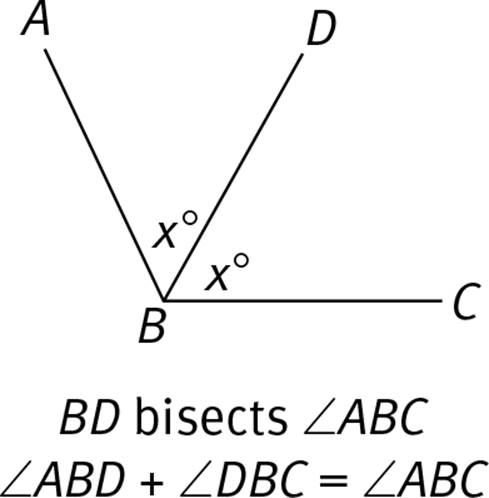
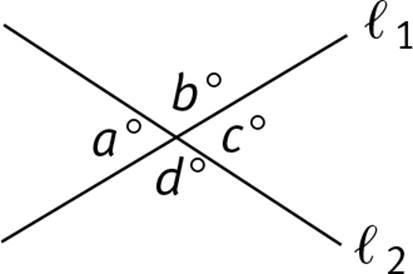
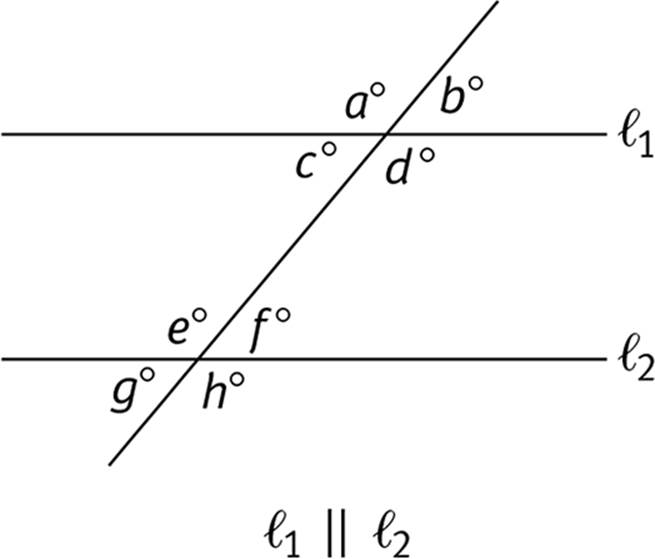
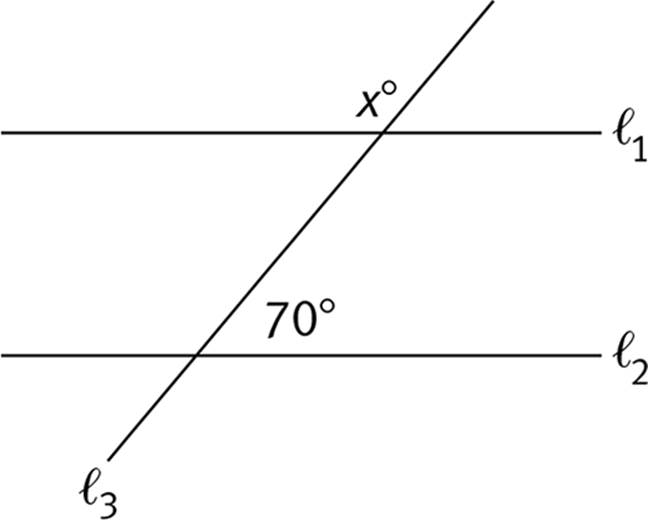

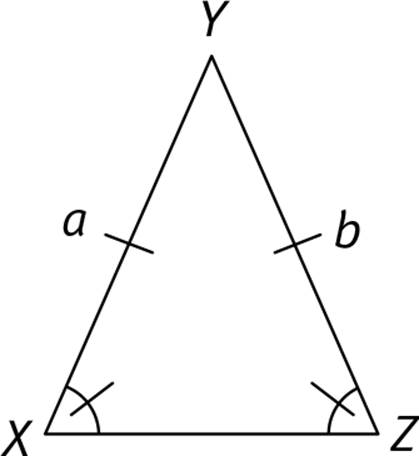
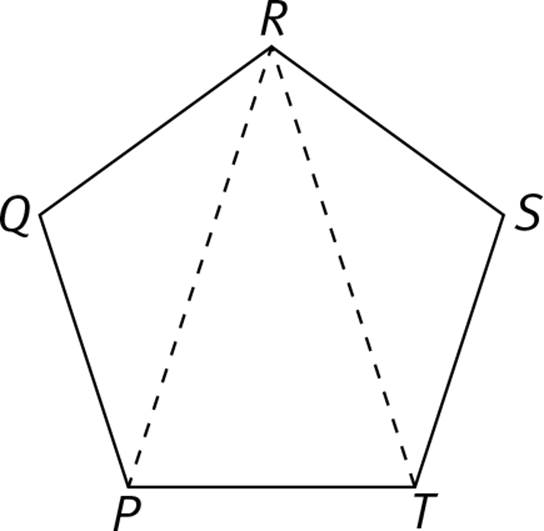
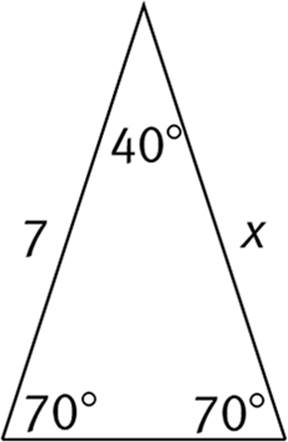
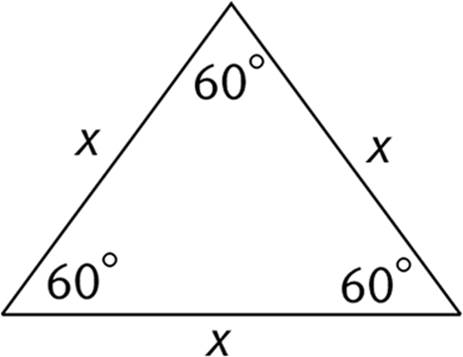
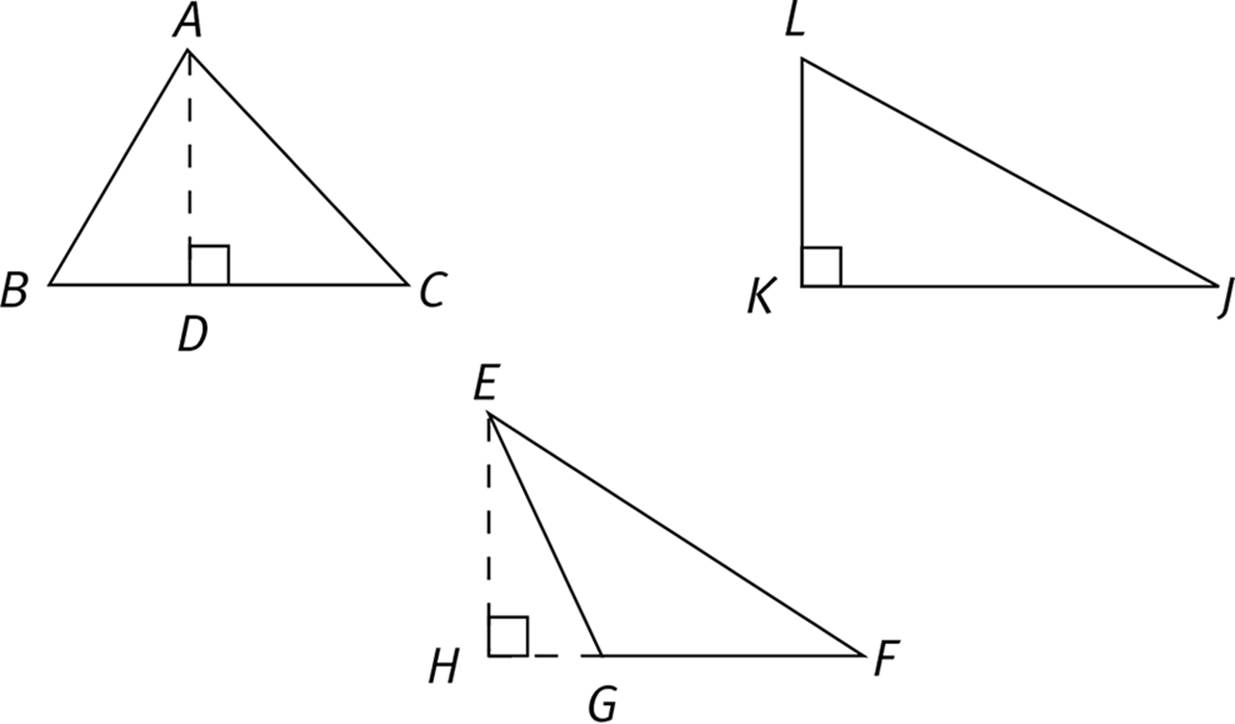 In the diagrams above, AD, EH, and LK are altitudes.
In the diagrams above, AD, EH, and LK are altitudes.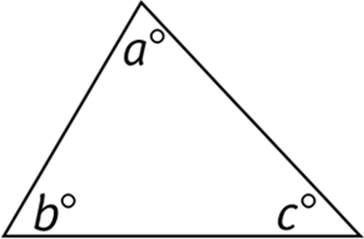
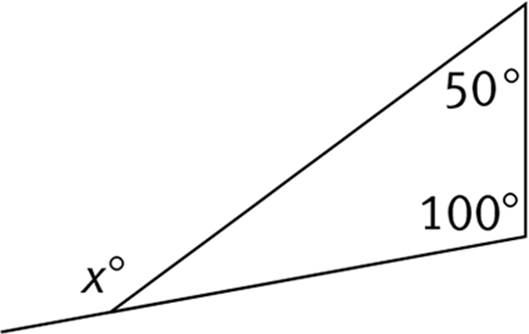
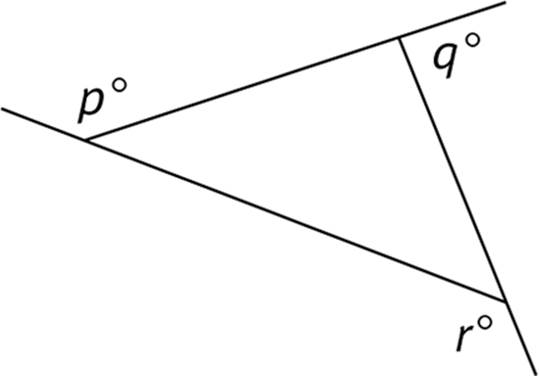
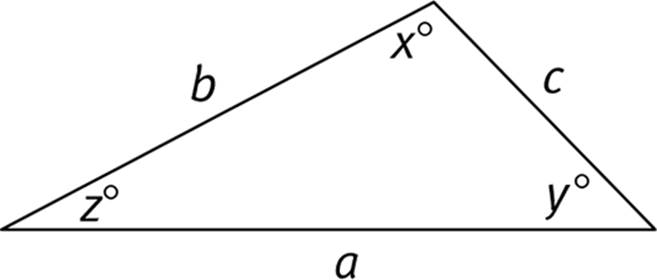
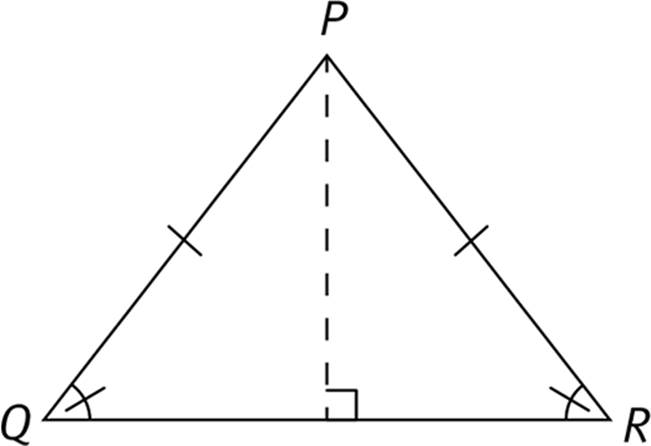
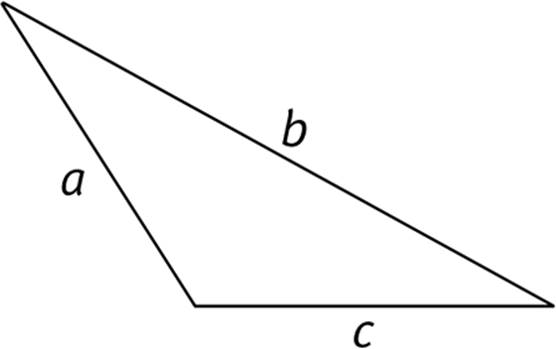
![]() find the perimeter of the triangle above in terms of a.
find the perimeter of the triangle above in terms of a.![]()
![]()
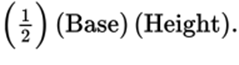
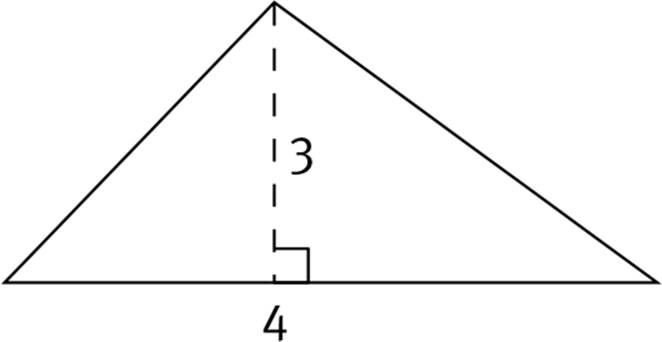
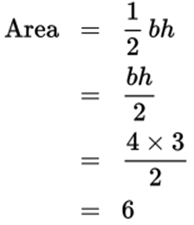
![]()

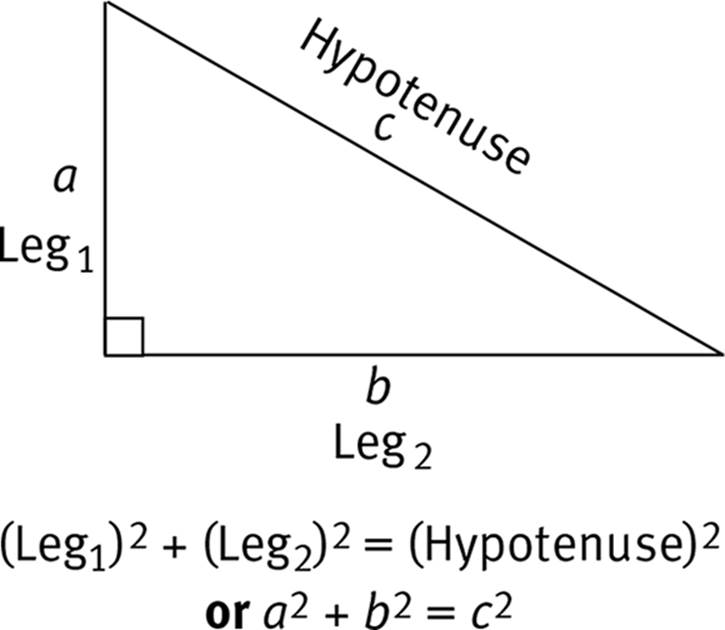
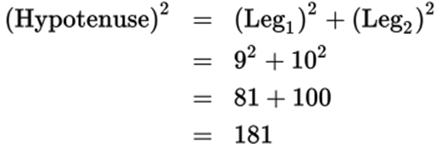
![]()
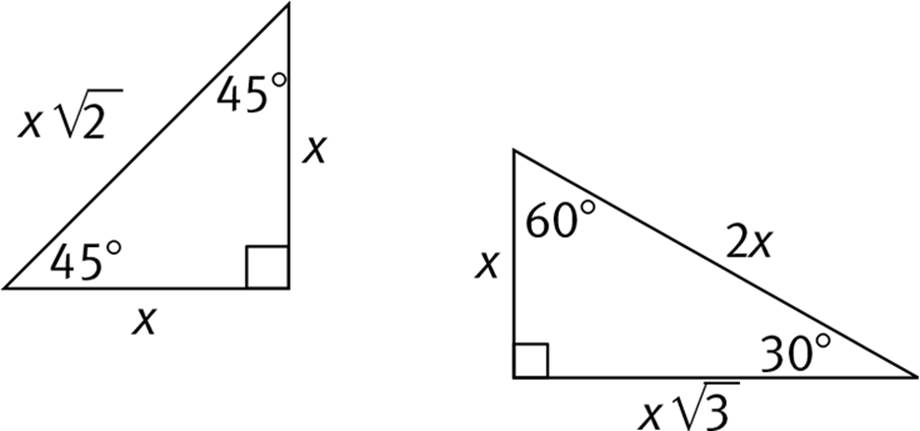
![]() with the
with the ![]() in the ratio representing the hypotenuse. The sides of a 30°/60°/90° right triangle are in a ratio of
in the ratio representing the hypotenuse. The sides of a 30°/60°/90° right triangle are in a ratio of ![]() where 2x represents the hypotenuse and x represents the side opposite the 30° angle. (Remember: the longest side has to be opposite the greatest angle.)
where 2x represents the hypotenuse and x represents the side opposite the 30° angle. (Remember: the longest side has to be opposite the greatest angle.)![]() Since the length of a leg is 4, the length of the hypotenuse must be
Since the length of a leg is 4, the length of the hypotenuse must be ![]()
![]()
![]() but it’s also possible that AC, the missing side, is the hypotenuse. In that case, the area would be
but it’s also possible that AC, the missing side, is the hypotenuse. In that case, the area would be ![]() Because Quantity A can either be equal to Quantity B or can be larger than Quantity B, their relationship cannot be determined from the information given.
Because Quantity A can either be equal to Quantity B or can be larger than Quantity B, their relationship cannot be determined from the information given.
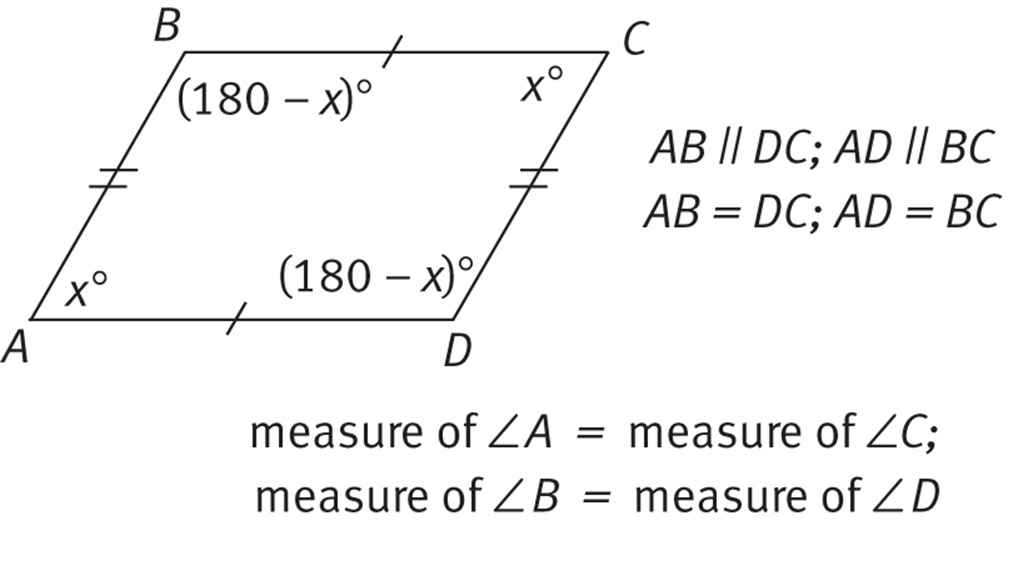
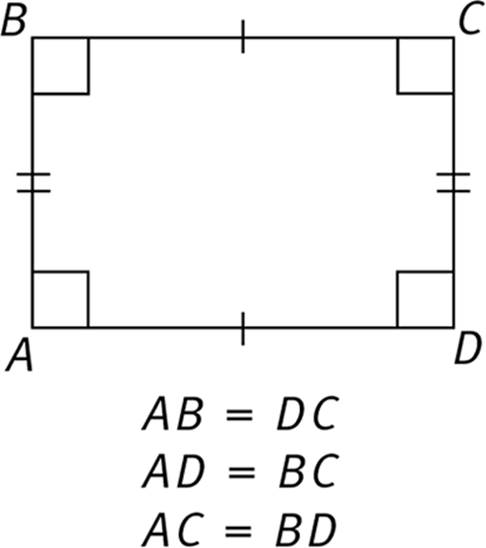
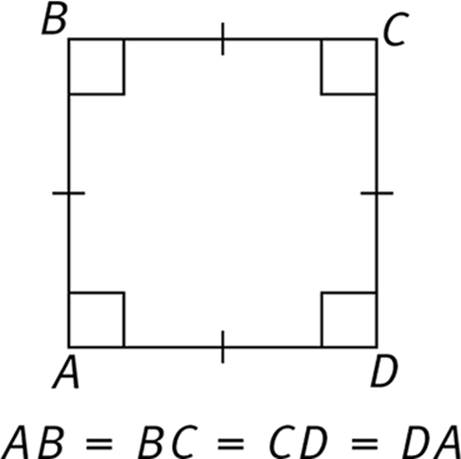
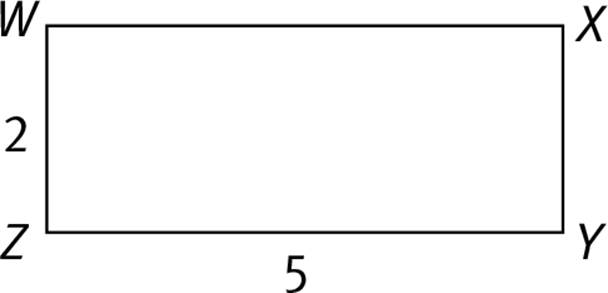
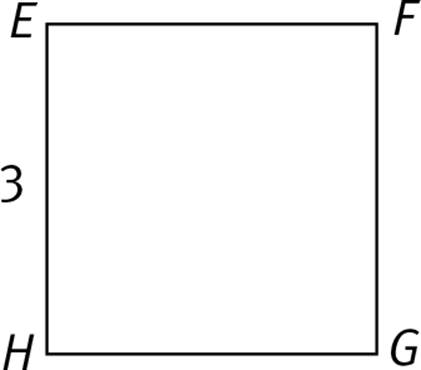
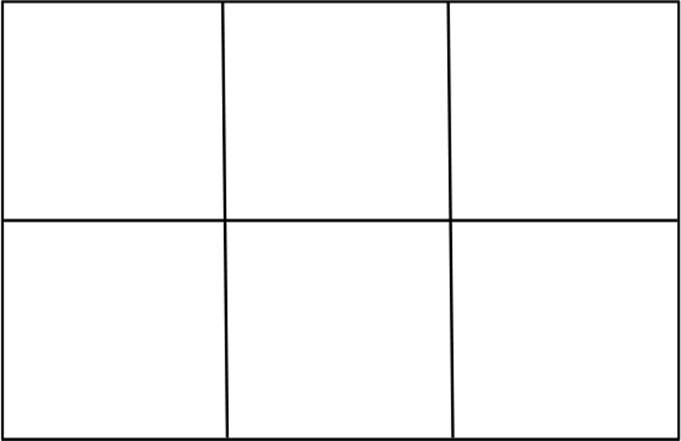
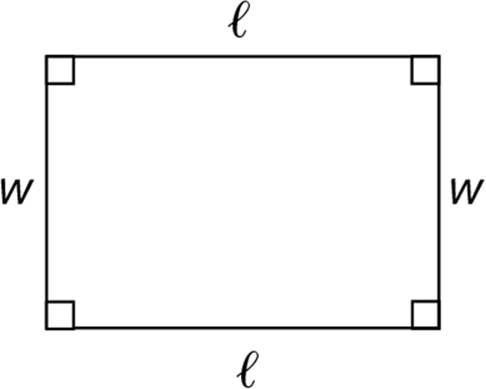
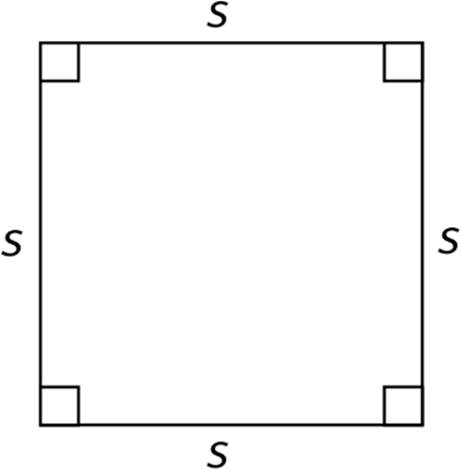
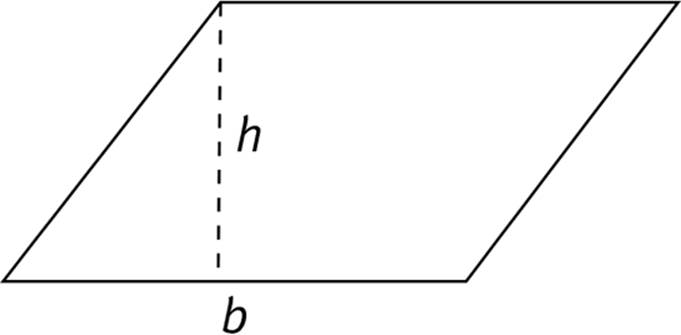

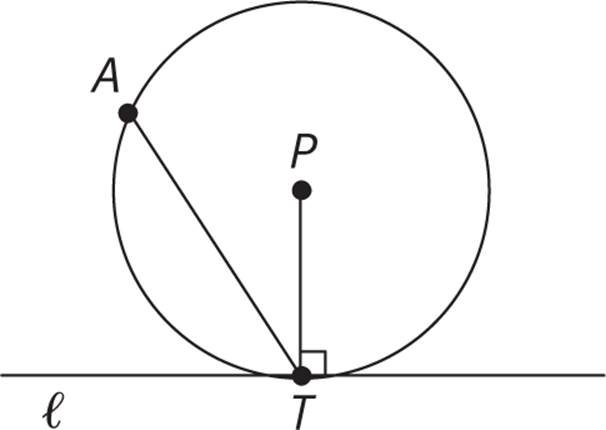
![]()
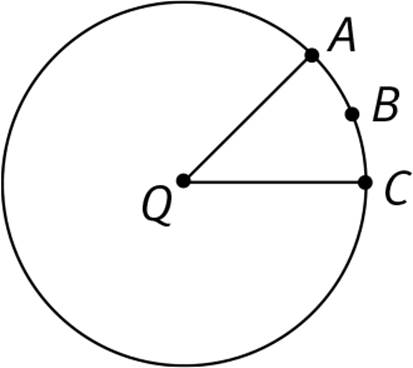
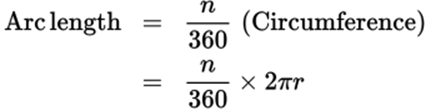
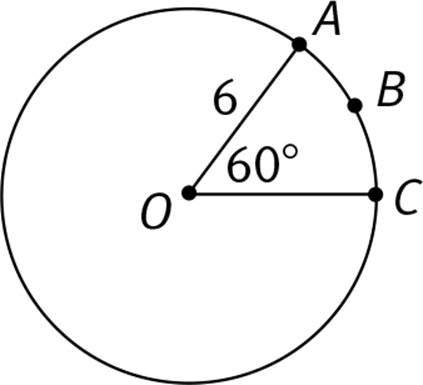
![]() or
or ![]() of the circumference. Thus, the length of arc ABC is
of the circumference. Thus, the length of arc ABC is ![]() or 2π.
or 2π.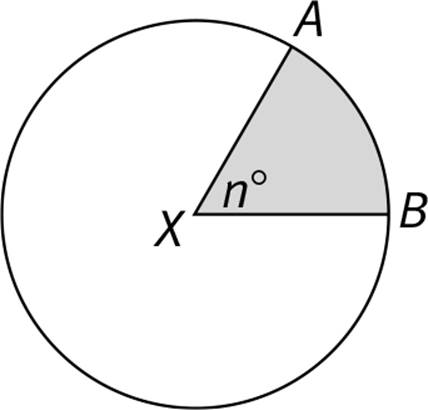
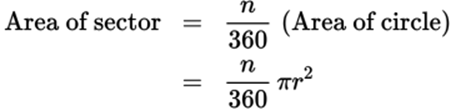
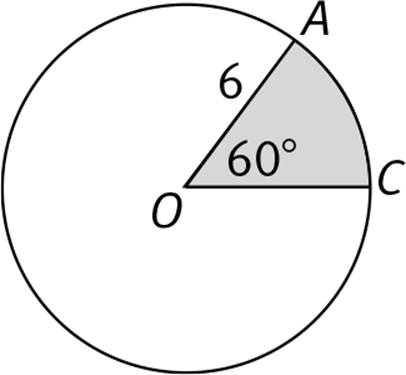
![]() or
or ![]() of the total area of the circle. Therefore, the area of the sector is
of the total area of the circle. Therefore, the area of the sector is ![]()

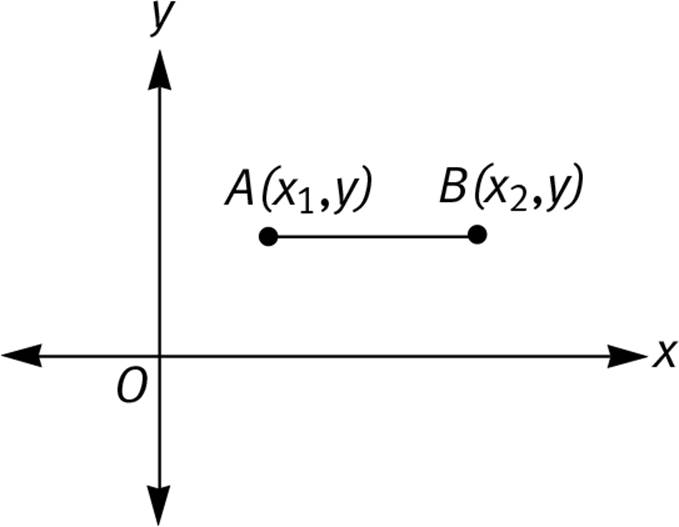
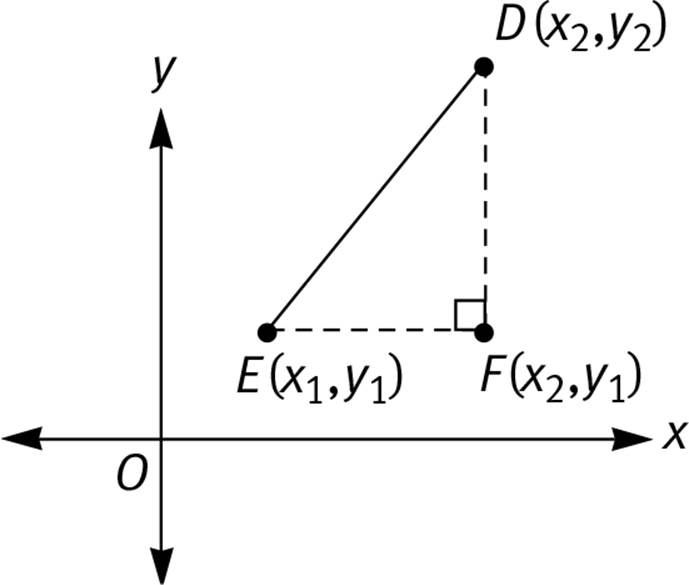
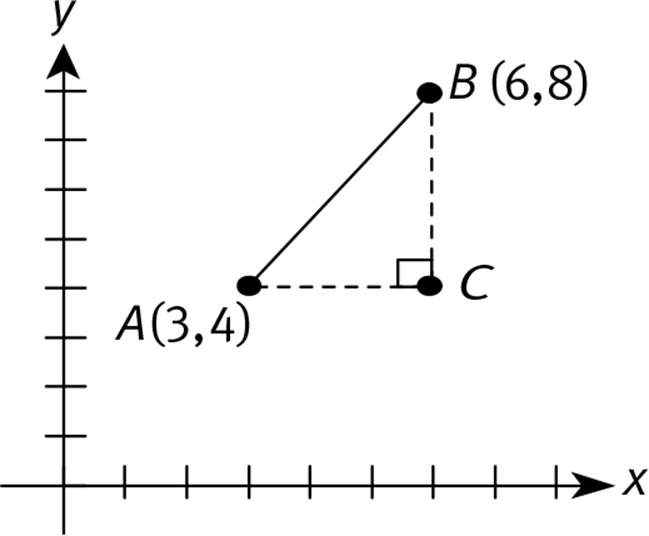
![]() and b is the point where the line intercepts the y-axis, that is, the value of y where x = 0.
and b is the point where the line intercepts the y-axis, that is, the value of y where x = 0.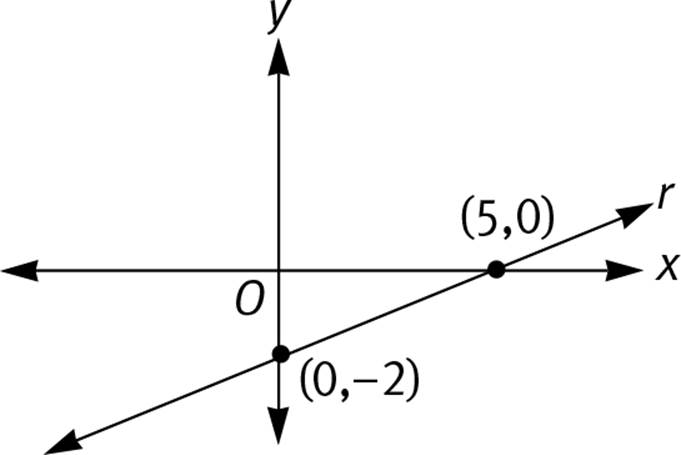
![]() That makes the slope-intercept form
That makes the slope-intercept form ![]()
![]() which simplifies to 2 = 4 − 2.
which simplifies to 2 = 4 − 2.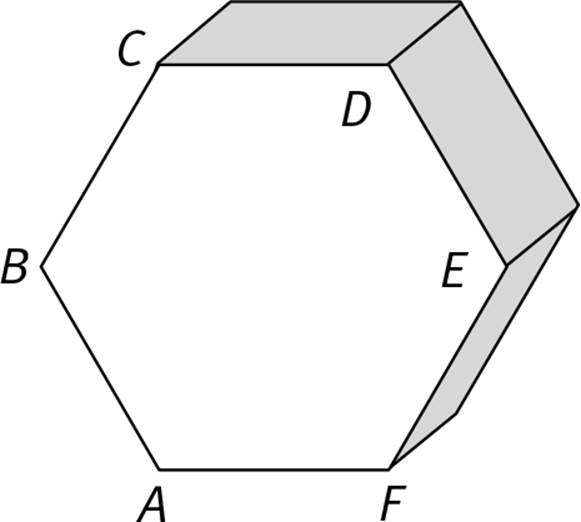
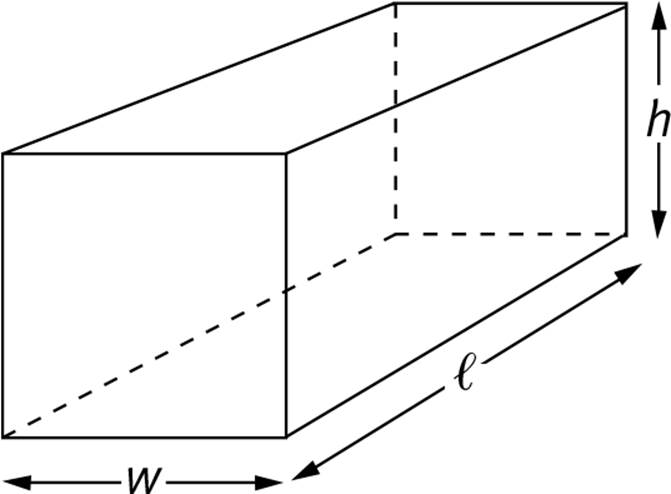
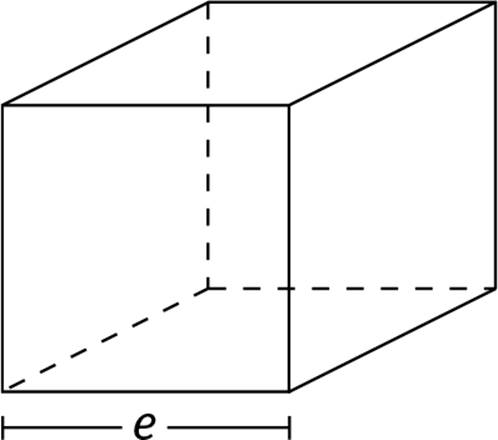
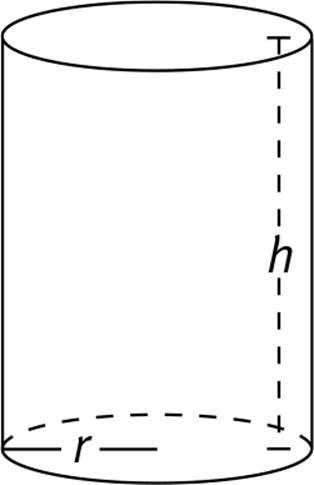
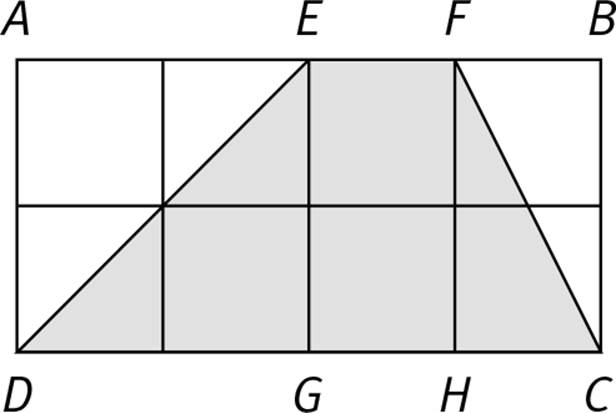
![]() or 3.
or 3.![]() The area of rectangle EFHG is (3)(6), or 18. The area of triangle FHC is
The area of rectangle EFHG is (3)(6), or 18. The area of triangle FHC is ![]() or 9. The total shaded area is 18 + 18 + 9, or 45.
or 9. The total shaded area is 18 + 18 + 9, or 45.![]() or 18. The area of unshaded right triangle FBC is
or 18. The area of unshaded right triangle FBC is ![]() or 9. Therefore, the total unshaded area is 18 + 9 = 27. Subtract the total unshaded area from the total area of rectangle ABCD: 72 − 27 = 45.
or 9. Therefore, the total unshaded area is 18 + 9 = 27. Subtract the total unshaded area from the total area of rectangle ABCD: 72 − 27 = 45.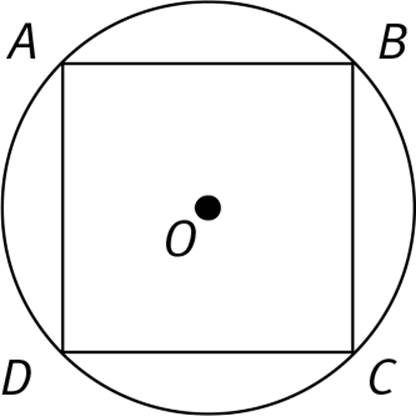
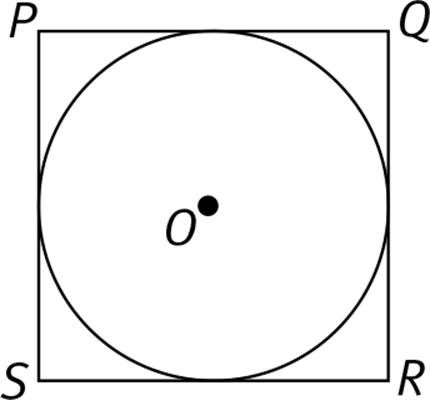
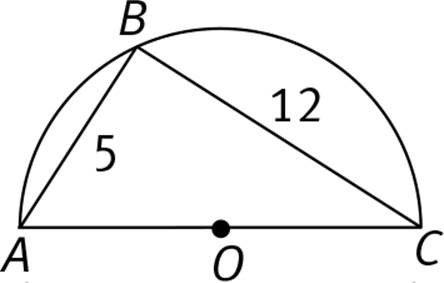
![]() , what is the circumference of the circle with center O?
, what is the circumference of the circle with center O?![]()