LSAT For Dummies, 2nd Edition (2014)
Part II. Analytical Reasoning: Following the Rules of the Logic Game
Chapter 6. Type Casting: Grouping Games
In This Chapter
![]() Recognizing grouping games and which type they are
Recognizing grouping games and which type they are
![]() Understanding the three kinds of game conditions
Understanding the three kinds of game conditions
![]() Considering rule implications to extend your game board
Considering rule implications to extend your game board
![]() Practicing on sample grouping games
Practicing on sample grouping games
In addition to ordering games, which we cover in Chapter 5, the LSAT analytical reasoning section presents another logic game type we call grouping games. These games ask you to categorize the elements, or game pieces, into two or more groups in accordance with several rules or conditions. Grouping games may appear at first to be more complicated than they are. This chapter provides you with an approach that breaks down and simplifies them and puts you in control of the game board.
Several kinds of grouping games exist, but the general way you handle them doesn't vary. Consider the facts and rules, create a game board, and leap into the questions with confidence.
Classifying Grouping Games
One way to identify grouping games is by recognizing the language the facts and rules don't use. Although some grouping games may also include an element of ordering, most are noticeably bereft of ordering references, such as first/last, higher/lower, and before/after. Instead, the facts and rules contain wording that suggests matching one set of elements to another set or two of elements. Look for words that indicate group membership, such as included, on the team, with, and together.
 Another way to confirm whether a game is of the grouping variety is by reading its first question. Usually, the first question of a grouping game asks you for a possible assignment of game pieces to categories. The answer choices often list each group name followed by a colon and a list of the game pieces included in that group. When the first question in the set exhibits this format, you're likely dealing with a grouping game.
Another way to confirm whether a game is of the grouping variety is by reading its first question. Usually, the first question of a grouping game asks you for a possible assignment of game pieces to categories. The answer choices often list each group name followed by a colon and a list of the game pieces included in that group. When the first question in the set exhibits this format, you're likely dealing with a grouping game.
After you know you have a grouping game, engage in another categorization. Grouping games come in two general types:
· In/out: The facts for this game type reference one group, to which game pieces either belong or don't belong. If a game piece belongs, it's in. If not, it's out. You can designate these two options on your game board as in/out, yes/no, +/–, or whatever works for you.
· Classification: This type's fact pattern names two or more groups to which you assign the game pieces. Designate the groups on your game board by name.
To help you distinguish between the two grouping game types, take a look at a couple of simple sample fact patterns. An in/out type mentions just one group, like this:
A stylist has access to exactly seven accessories — belt, earrings, hat, glasses, necklace, ring, and scarf. The stylist accessorizes one outfit with exactly five of these accessories. The stylist selects the five accessories for the outfit in accordance with these specifications:
From these facts, you create one group of accessories, the group of five that beautifies the outfit. Five accessories belong on the outfit, and two don't. To record this information on a game board, list the game pieces (first initials of the seven accessories) and create a box chart that indicates that five pieces belong and two don't:
![]()
A classification fact pattern, like this one, specifically names two or more groups:
Exactly five zoo animals — gnu, peacock, snake, yak, and zebra — are moved into three habitats — A, B, and C. Exactly two animals are moved into A, exactly two animals are moved into B, and exactly one animal is moved into C. The assignment of animals to habitats must adhere to the following conditions:
These facts define three groups — A, B, and C — and five game pieces — g, p, s, y, and z. List the game pieces and form a box chart with the group designations as column headings. This simple scenario states exactly how many members exist in each group, so you can record the appropriate number of spaces under each group name, like this:

Most LSAT grouping games are more complex than these sample scenarios. The facts may provide additional qualifiers. (For example, the stylist scenario could also state that each accessory is colored either silver or gold.) Group assignments may be left open. (For example, the zoo animal scenario may not clarify exactly how many animals are moved into each habitat.) Regardless of the grouping game's complexity, the game board you construct usually follows the same general format as the ones you've constructed for the sample scenarios.
Following the Rules of Division
In grouping games, the fact pattern is followed by the set of rules or conditions that restrict the group arrangements. Grouping game rules generally fall into three types: targets, joiners, and if/then statements.
Target rules
Targets give you concrete evidence about which group a game piece belongs or doesn't belong to. You can record a target directly on the box chart.
Clues that tell you exactly which group a piece belongs to are rare on the LSAT. Here's an example of a target rule for the in/out game in the preceding section:
· The stylist does not select the belt.
You can record this target directly on the box chart, like this:
![]()
A sample target rule for the classification game in the preceding section could be this:
· The gnu is moved into habitat C.
And the box chart would look like this:

Some rules don't tell you exactly which group a piece belongs to, but they narrow the options so significantly that we classify them as targets as well. Here's an example for the in/out game:
· The stylist selects either the hat or the glasses, but not both.
These two conditions allow you to record information on the box chart. Knowing that either the hat or the glasses (but not both) are selected gives you two options for the box chart:

The LSAT may also convey this same condition with a set of two if/then rules, like this:
· If the hat is selected, the glasses are not selected.
· If the glasses are not selected, the hat is selected.
 Knowing that if the hat is selected, the glasses aren't selected doesn't give you enough information to determine that H and G are always separate. Without the presence of the second rule, you only know what happens when each item is selected. You can't make assumptions about what happens when one is not selected. So without the presence of the second rule, it may be possible that both H and G are not selected. We further discuss the implications of if/then rules in the upcoming section “If/then rules.”
Knowing that if the hat is selected, the glasses aren't selected doesn't give you enough information to determine that H and G are always separate. Without the presence of the second rule, you only know what happens when each item is selected. You can't make assumptions about what happens when one is not selected. So without the presence of the second rule, it may be possible that both H and G are not selected. We further discuss the implications of if/then rules in the upcoming section “If/then rules.”
For the classification game, you may see a target rule like this one:
· The yak is moved to either habitat A or habitat C.
If the yak is in either A or C, you know the yak can't be moved to habitat B. Record this rule by showing where the yak can't belong:

Joining rules
Joining rules specify game pieces that are always assigned to the same group. Depending on the game, you may or may not be able to record joining rules in the box chart. In/out games have only two possible groups, so for these games, joining rules provide two possible assignments. The game pieces are either both in or both out. Here are some examples of joining rules for the in/out game regarding the stylist:
· Either both the ring and the scarf are selected or neither is selected.
· The ring is selected if and only if the scarf is selected.
These two rules give you the same information: If S = in, R = in, and if S = out, R = out. Record the options on your box chart:

A possible joining condition for the classification game could be this:
· The peacock is moved into the same habitat as the zebra.
This rule gives you two valuable clues:
· The peacock and zebra are together.
· The peacock and zebra can't occupy habitat C because it has space for only one animal.
You can record these clues on your game board by writing pz under the box chart and entering p and z with slashes through them in the C column of the box chart.

If/then rules
Grouping games commonly provide or suggest if/then statements in the rules. These statements are logically equivalent to their contrapositive statements, which are created by inverting and flipping the two parts of the statement.
Every if/then statement has two parts: the if and the then. In a conditional statement, these two parts are both positive, like this:
· If the earrings are selected, the necklace is selected.
The contrapositive of a conditional statement reverses the order of the two parts and makes them negative:
· If the necklace is not selected, the earrings are not selected.
The contrapositive of an inverse statement (where both parts are negative) is also true. So knowing that “if the earrings are not selected, the necklace is not selected” also tells you that “if the necklace is selected, the earrings are selected.”
You may also find the contrapositive of statements with negative and positive parts. So “if the necklace is not selected, the earrings are selected” also means that “if the earrings are not selected, the necklace is selected.”
 To find the contrapositive of any if/then statement, follow these two steps:
To find the contrapositive of any if/then statement, follow these two steps:
1. Put the second part of the statement first and the first part second.
2. Make the positive statements negative and the negative statements positive.
Apply the two steps to this if/then condition:
· If the necklace is not selected, the ring is not selected.
Start the contrapositive statement with the second part, the ring, and change the original negative statement to a positive: “If the ring is selected.” End the statement with the first part and change its negative to a positive: “the necklace is selected.” The contraposition statement is this:
· If the ring is selected, the necklace is selected.
We like to use arrows for if/then statements, so we record the if/then rule and its contrapositive on the game board like this:

 Whenever you see an if/then statement in a logic game, you know that its contrapositive is also true.
Whenever you see an if/then statement in a logic game, you know that its contrapositive is also true.
 Follow the steps to forming contrapositives exactly. You can't form the contrapositive of an if/then statement by just reversing the parts. You must also switch the positives and negatives. So knowing that “if the necklace is not selected, the ring is not selected” does not tell you that “if the ring is not selected, the necklace is not selected.”
Follow the steps to forming contrapositives exactly. You can't form the contrapositive of an if/then statement by just reversing the parts. You must also switch the positives and negatives. So knowing that “if the necklace is not selected, the ring is not selected” does not tell you that “if the ring is not selected, the necklace is not selected.”
As you record each condition, consider how you may extend it to further develop your game board. You can better complete your board by expanding on the implications of individual rules and by combining rules that involve the same game pieces. Rules that offer contingencies may allow you to split the box chart and open up your ordering options. When you spend quality time extending your game board, you spend less time answering the questions.
Expanding the Grouping Game Board
Before you leap into the questions for a grouping game, you want to extend the rules and play with a few possible group assignments to become familiar with how the rules limit the game. Take a look again at the zoo animal game with a couple of rules included:
Exactly five zoo animals — gnu, peacock, snake, yak, and zebra — are moved into three habitats — A, B, and C. Exactly two animals are moved into A, exactly two animals are moved into B, and exactly one animal is moved into C. The assignment of animals to habitats must adhere to the following conditions:
· The peacock is moved into the same habitat as the zebra.
· The yak is moved to either habitat A or habitat C.
When you create a game board for this game and record the rules, you get something like this:

This board may not seem like much to go on at first, but consider some of the possible assignments. The yak (y) can occupy only A or C. Moving y to A is very limiting. The animals p & z have to be moved to B because B would be the only habitat with two spots for them to share. Only two possible combinations exist when y = A. They are A: y & g; B: p & z; C: s or A: y & s; B: p & z; C: g.
Moving y to habitat C is also limiting; p & z occupy either A or B, and g & s occupy whichever habitat p & z don't. After careful consideration of the two rules, you can record the four possible combinations on your game board:
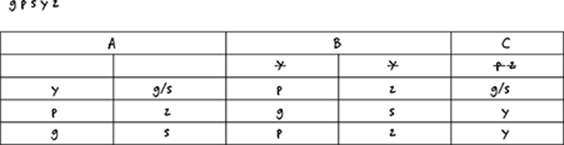
 When you take a few moments to consider the implications of the rules, you often find that you're left with a limited number of possible assignments.
When you take a few moments to consider the implications of the rules, you often find that you're left with a limited number of possible assignments.
The grouping games you encounter on the LSAT aren't usually as simple as the zoo animal scenario. Most make the problem more complex by introducing an additional grouping factor or by leaving open the number of pieces assigned to each group. For example, the zoo animals may be additionally classified as mammal or non-mammal, or the game may not specify the number of animals moved to each of the three habitats. Regardless of the game's complexity, however, you create each grouping game board in the same general way:
1. Record the game pieces on your game board.
2. Isolate the main groupings and use them to head the columns of your box chart.
3. Record the rules.
4. Consider several possible group assignments.
When you finish these four steps, you're ready to tackle the questions. Refer to Chapter 4 to review the approach to answering logic game questions. We cover the process in detail in the next section, where you work through examples of a simple and more complex grouping logic game.
Mastering Practice Grouping Games
The best way to get a handle on the grouping logic games is to walk through a few games step by step. The first few logic games you face can be a bit daunting (okay, very daunting), but remember, you can solve them by following the steps. And with practice, the steps will become as familiar as your walk home. If you start to feel panicky, take a deep breath and just take the next step. Don't get caught up in what you don't know; apply what you do know. Here are a couple of practice problems to help you out.
An in/out grouping game
Try your skills on an in/out grouping game.
 A building contractor creates a team of exactly six professionals to work on a construction site. He chooses from three plumbers: Harry, Ingrid, and James; three carpenters: Mary, Nick, and Oliver; and three tile installers: Andrew, Bert, and Ernestine. The contractor observes the following conditions in forming the team:
A building contractor creates a team of exactly six professionals to work on a construction site. He chooses from three plumbers: Harry, Ingrid, and James; three carpenters: Mary, Nick, and Oliver; and three tile installers: Andrew, Bert, and Ernestine. The contractor observes the following conditions in forming the team:
· If Oliver is selected for the team, Andrew is not selected.
· If James is selected for the team, Harry is not selected.
· If James is selected for the team, Mary is also selected.
· If Mary is selected for the team, Oliver is also selected.
The construction workers are either among the six who are in the group (+) or among the three who are out of the group (–). You know exactly six of the nine workers will be in and three will be out.
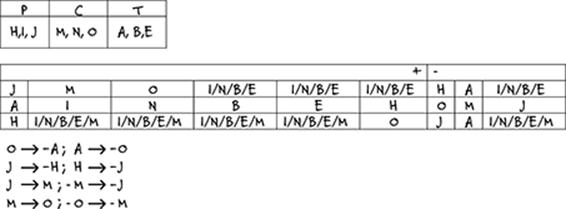
Start building your game board immediately. Forget the names; list the workers by letter underneath the headings of P, C, and T to keep track of each worker's profession. Create a box chart with nine columns, six for the team members and three for those who are left out. You start with a game board like this:

Analyze the rules. All provide if/then statements. The first tells you that if O is in, A is out. So it's also true that if A is in, O is out, and O and A are never both in. Record these facts on your game board. The second rule is the same: If J is in, H is out, and if H is in, J is out. Keep track on your game board.
The third rule is a little different. It tells you that if J is in, M is in. You also know the contrapositive — that if M is out, J is out. That's the same as saying that you can't have J without M (but you can have M without J). The fourth rule is similar to the third. It states that if M is in, O is in. So you also know that if O is out, M is out. Record these rules on your game board.
Expand the game board by considering possible group assignments. Start with J because he's a part of many rules. When J is in, M is in, and when M is in, O is in. Add J, M, and O to the + side of the box chart. When J is in, H is out, so put H on the – side. O is in, so add A to the – side, too. The remaining three spots could be filled with I, N, B, or E.
When A is in, O is out, and when O is out, M is out. Add an option to your game board with A on the + side and O and M on the – side. One space remains on the – side. That space has to be either J or H because they can't both be in, and it has to be J because if you put J on the + side, you have to have M there too. So J is on the – side, and H, I, N, B, and E have to be on the + side of the chart.
The second option provides one possible assignment with H on the + side and J on the – side. Is there another possibility? With H on the + side, the – side could be J, A, and any one of I, N, B, E, or M. The four remaining pieces belong on the + side with O. Your game board looks like this, which should give you enough information to tackle the questions:
 Which one of the following is an acceptable team of construction workers?
Which one of the following is an acceptable team of construction workers?
(A) Ingrid, James, Mary, Oliver, Bert, Ernestine
(B) Ingrid, James, Nick, Oliver, Bert, Ernestine
(C) Harry, James, Mary, Nick, Bert, Ernestine
(D) Harry, James, Mary, Oliver, Andrew, Bert
(E) Harry, Ingrid, Mary, Nick, Bert, Ernestine
The first question almost always asks for an acceptable assignment. Despite the work you've devoted to developing the game board, ignore it for now and answer this question by examining each of the four rules. The first rule says that if O is in, A is out. Choice (D) puts both O and A on the + side, so it's wrong. The second rule states that if J is in, H is out. Eliminate Choice (C) because it has both J and H on the + side. The third rule specifies that when J is in, M is in. Choice (B) has J with no M, so it's incorrect. The fourth rule requires O to be in when M is in. Choice (E) has M with no O, so it's out. The correct answer that doesn't violate a rule is Choice (A).
 If Harry and Oliver are included on the team, then which one of the following must be true?
If Harry and Oliver are included on the team, then which one of the following must be true?
(A) Exactly two tile installers are on the team.
(B) All three carpenters are on the team.
(C) Mary is not a member of the team.
(D) James is a member of the team.
(E) Andrew is not a member of the team.
This add-a-rule question requires an answer that must be true. (For more information on question types, see Chapter 4.) The temporary rule is that H and O are on the + side. The third line of the box chart gives you possible arrangements when H and O are on the team. Refer to that line to eliminate answers that either could be true (but don't have to be) or must be false. Choice (A) could be true if the team included H, B, E, I, N, and O, but it isn't true when the team assignment is H, B, M, I, N, and O. Choice (A) doesn't have to be true, so it's wrong. Likewise, M, N, and O could be on the team together but don't have to be, so Choice (B) is out. Mary either could or couldn't be a member of the team, so Choice (C) is wrong. In no case can J be on the + side, so Choice (D) has to be false. The only answer that must be true is Choice (E). In all cases where H and O are on the + side, A is on the – side.
 Each of the following pairs of workers could be included together on the team EXCEPT:
Each of the following pairs of workers could be included together on the team EXCEPT:
(A) Ingrid and James
(B) Mary and Oliver
(C) James and Andrew
(D) Bert and Ernestine
(E) Mary and Ernestine
Eliminate answers that could be pairs of team members. The first option in the box chart shows I and J on the team together, so cross out Choice (A). It also puts M and O on the team together, so Choice (B) is wrong. No option shows J and A on the team together, so it's likely the correct answer. Check the last two answers to be sure. B and E work together in most assignments, so Choice (D) is out. You can put M and E together when J is on the team and when H is on the team, so Choice (E) is wrong. The correct answer is Choice (C).
A more complex grouping game
Some of the more complex logic grouping games introduce an element of ordering. We classify them as grouping games, though, because they require more grouping than ordering. Here's an example of one of these more complicated grouping games.
 Five graduate assistants — Quinlan, Roberts, Solomon, Trujillo, and Verma — are assigned to supervise recitation sessions in three classrooms — Fox Hall, Hepburn Hall, and McIntyre Hall. Each classroom is supervised by at least one of the graduate assistants, and each graduate assistant supervises exactly one classroom. Each of the three recitation sessions takes place on a different day. The supervisory schedule must adhere to the following specifications:
Five graduate assistants — Quinlan, Roberts, Solomon, Trujillo, and Verma — are assigned to supervise recitation sessions in three classrooms — Fox Hall, Hepburn Hall, and McIntyre Hall. Each classroom is supervised by at least one of the graduate assistants, and each graduate assistant supervises exactly one classroom. Each of the three recitation sessions takes place on a different day. The supervisory schedule must adhere to the following specifications:
· The Fox Hall recitation must be held before the Hepburn Hall recitation.
· The Fox Hall recitation is supervised by only one of the graduate assistants.
· The recitation that is supervised by Quinlan must be held before the recitation that is supervised by either Roberts or Trujillo.
· The recitation that is supervised by Solomon cannot be held after any recitation that is supervised by Verma.
At first the ordering language may lead you to believe that this is just an ordering game, but when you check the answers to the first question, you see that the five graduate assistants are also grouped together by recitation location. That indicates that you're working with a grouping game with ordering thrown in to make things interesting.
First list the game pieces, the first initials of the graduate assistants — Q, R, S, T, and V. The three groups in this classification grouping game are the three recitation classrooms: F, H, and M. These are the column headings for your box chart. But note that the order of the columns matters, so you may want to wait until you've evaluated the rules before you create the box chart.
Before you check out the rules, however, consider the grouping possibilities. You're putting five game pieces into three groups. You use all five pieces and classrooms, so the possible groupings could be two in one group, two in another, and one in the other or three in one group, one in another, and one in the other.
The first rule says that F is before H, or F → H. Record that rule on your game board, along with the three possible orders of the recitations: (1) FHM, (2) MFH, or (3) FMH. The next rule says that F has only one member. For now, remember the rule by writing F = 1 on the board.
The third rule says that Q → R and Q → T. The last rule states that S can never supervise a session after V, so S → V or S supervises with V. Record these rules and expand the board by considering their implications. If Q → R and Q → T, Q can't be last, and R and T can't be first. For more about evaluating ordering rules, see Chapter 5.
 Be careful with the last rule. It states that S can't be included in a recitation after one that V is part of. So S → V or S can = V. S and V can be in the same recitation without violating the condition that S can't be after V. You know that V can't be first without S and S can't be last without V.
Be careful with the last rule. It states that S can't be included in a recitation after one that V is part of. So S → V or S can = V. S and V can be in the same recitation without violating the condition that S can't be after V. You know that V can't be first without S and S can't be last without V.
You don't know the order of the recitations, so start out by creating a box chart with three columns. The first column heading can be either F or M; the last column heading can be either M or H. If F is first, the first group can include only Q or S because F has only one supervisor, R and T can't supervise first, and V can't supervise in the first position alone. If M is first, then the first group could have one (Q or S), two (QS or SV), or three (Q, S, V) supervisors. Initially, your game board may look something like this:
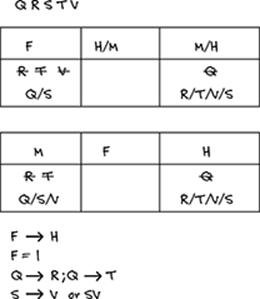
If the first group is F, it includes either only Q or only S. If only Q supervises first, the possible groupings are numerous. Your main job is to make sure V doesn't come before S, so S could be in the second column with or without V or in the third column with V. R and T can be in either column as long as no column is empty. If the first group is supervised by only S, R and T have to be in the third column so they can follow Q, which therefore must be in the second column. V can be in either column.
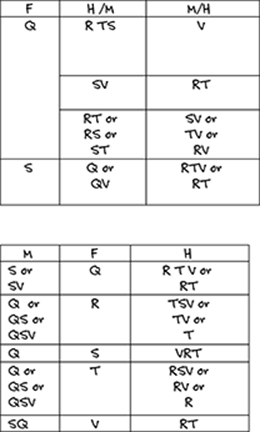
If the first group is M, F must head the second column, and H must head the third column. F can have only one supervisor. If that supervisor is Q, then R and T have to be in the third column, and S must occupy the first column. V could go with S in the first column or with R and T in the third column. If R is alone in the second column, Q has to be before R in the first column, and T has to be in the third column. S and V can occupy the first or third column as long as V isn't before S. If S is alone in the second column, V has to be in the third column, R and T have to join V, and Q has to be in the first column. If T is in the second column, Q has to be in the first column, and R has to be in the third column; S and V can be in the first or third column as long as V isn't before S. If V is alone in the second column, S has to be in the first column with Q, and R and T have to be in the third column.
You can record some of the possible groupings on your game board, like this:
Use the rules to eliminate answers to the first possible assignment question.
 Which one of the following could be the graduate assistants assigned to each of the recitation classrooms, with the recitation classrooms listed in the order in which they are supervised?
Which one of the following could be the graduate assistants assigned to each of the recitation classrooms, with the recitation classrooms listed in the order in which they are supervised?
(A) Fox Hall: Quinlan
Hepburn Hall: Roberts, Solomon
McIntyre Hall: Trujillo, Verma
(B) Fox Hall: Quinlan
Hepburn Hall: Roberts, Verma
McIntyre Hall: Solomon, Trujillo
(C) Fox Hall: Roberts
McIntyre Hall: Quinlan, Trujillo
Hepburn Hall: Solomon, Verma
(D) Hepburn Hall: Solomon
Fox Hall: Quinlan
McIntyre Hall: Roberts, Trujillo, Verma
(E) McIntyre Hall: Quinlan
Fox Hall: Roberts, Solomon
Hepburn Hall: Trujillo, Verma
Eliminate answers that violate rules. The first rule is F → H. Choice (D) puts H before F, so it's out. Choice (E) violates the second rule that F has only one member, so cross it off. The third rule is that Q → R and T. Choice (C) puts Q after R, so it's wrong. The last rule says that S is not after V. Eliminate Choice (B) because it violates this final rule. The remaining answer, Choice (A), is correct.
 If one of the recitations is supervised by both Quinlan and Solomon, which one of the following could be true?
If one of the recitations is supervised by both Quinlan and Solomon, which one of the following could be true?
(A) The recitation in Fox Hall is the first of the three recitations.
(B) The recitation in Hepburn Hall is the second of the three recitations.
(C) One of the recitations is supervised by only Verma.
(D) The second of the three recitations includes Solomon as a supervisor.
(E) The second of the three recitations includes exactly two of the graduate assistants as supervisors.
This question adds the rule that Q and S are included in the same group. According to your game board, that group has to be M and must be first. So Choice (A) has to be false. When M is first, F is second, so Choice (B) is incorrect. It's possible that the second visit could include only V. R and T would then be in the third group. Choice (C) is possible, but check the last two answers to be sure. S must be in the first group, so Choice (D) is wrong. Only one graduate assistant can supervise the second group, so Choice (E) is out. Choice (C) is correct.
 Which of the following must be true?
Which of the following must be true?
(A) The recitation in Fox Hall is held before the recitation in McIntyre Hall.
(B) The recitation that includes Verma is held earlier than the recitation that includes Roberts.
(C) One of the first two recitations includes Solomon as a supervisor.
(D) The second of the three recitations includes at least two graduate assistants as supervisors.
(E) At least one of the first two recitations includes only one of the graduate assistants as a supervisor.
Eliminate answers that could be true but don't have to be and answers that are always false. M can be held before F, so Choice (A) is out. Several groupings put R before V, so Choice (B) is wrong. One grouping where S is in the third group could be 1: Q, 2: RT, 3: SV, so eliminate Choice (C). When F is second, the second group has just one member, so Choice (D) doesn't have to be true. In all groupings, either the first or second group has just one member, so Choice (E) is correct.
 When you spend more time upfront considering the possible options for grouping games, you spend much less time answering the questions.
When you spend more time upfront considering the possible options for grouping games, you spend much less time answering the questions.
This last sample grouping game is just one of many ways the LSAT may test your ability to logically assign game pieces to groups in the analytical reasoning section. To expose yourself to the different kinds of possible grouping games, take the practice tests in this book, study a copy of LSAT Logic Games For Dummies, by Mark Zegarelli (Wiley), and purchase prior LSAT exams from the LSAC at www.lsac.org.